Received 17 September 2015; accepted 5 October 2015; published 8 October 2015

ABSTRACT

The article contains a model of wagon rolling down the hump profiles. It deals with motive and resistance forces. These forces made it possible to mathematically describe geometrical parameters of hump profile and kinematical characteristics of wagon movement depending on time. The conditions have been formulated, which makes the wagon movement down various marshalling hump profile sections possible. These conditions enable slowdown of the wagon as it moves from one hump profile element to the other until it stops in the hump-yard.

Keywords:

Marshalling Hump, Sliding Friction, Sliding with Rolling, Rolling Friction, Transverse Transferring Inertia Force, Aerodynamic Resistance Force, Reducing Force System to a Given Point, Coulomb Law, Retarded Heaviside Functions

Subject Area: Mechanical Engineering

1. Introduction

In [1] on the basis of critical analysis of the known works [2] [3] where the dynamic model of wagon rolling down hasn’t been built quite correctly, there has been demonstration of the account taken in moments of friction of wheels against rail threads and in box unit bearing in leading and rear trucks with their subsequent replacement by symbolic sliding friction. It has been observed that if the active force in the form of gravity force projection and aerodynamic resistance force toward the direction of wagon (or cut) rolling acting upon the wagon are larger than the ultimate friction force simultaneously with wheel rolling there can be also wheel sliding down rail threads. An analytical formula for finding the remainder of motive forces and all resistance forces under wheel rolling with sliding has been derived. The usage of principle of momentum of a material point [4] [5] made it possible to construct a mathematical model for finding the speed of a single wagon (or a cut) on the first profile hump section. It has been noted that the usage of principle momentum of a material point for finding the time of wagon rolling down the hump can be applied only when the wagon final speed is known otherwise the problem solution in such a form will prove to be meaningless. Due to this fact, in [1] speed finding should be considered as separate task requiring its solution based on drawing of differential equation of the movement [6] [7] .

In [2] on the assumption of uniformly accelerated wagon rolling down the hump, the formula for determining the braking force causing uniform wagon movement at constant speed has been found. As a result of analytical modeling of wagon movement on the section of the first braking position, various conditions which enable wagon movement on the first braking position section (1^st BP) at speed which is lower than the entrance speed have been formulated. There have been derived equations of wagon rolling speed and obtained final analytical formulas for finding the distance travelled, the movement time on the given length of the braking section making it possible the movement of a wagon (cut) with slowdown before switching area. Analytical formulas for determining braking distance have been obtained in a case when wagon motive forces are lower than the braking ones which may occur in case of non-observance of certain conditions.

In [6] [7] it has been noted that the development of theoretical fundamentals of calculation of wagon rolling by means of creating computational and constructing mathematical model on any hump section enabling the determination of rational geometrical parameters of hump profile and kinematic parameters of the wagon is a pressing problem of railway transport.

On this basis it should be observed that the determination of forces perceived by the wagon rolling down the hump profile is part of a still unsolved problem.

2. Formulation of a Problem

It is required to find all motive forces and resistance forces acting upon the wagon and emerging during its rolling down the hump profile because of the friction of wheels against rail threads, friction in bearings in box units and due to some other accidental forces with allowance made for the action upon the wagon (or the cut) of transverse transferring inertia force and head or/and fair wind.

3. Methods of Solution

Just as in [6] [7] we will consider the general case when the wagon is progressively rolling down the hump with a given initial speed 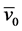(normally 4/5 km/h). While rolling down the hump the wagon will experience mainly the action of external forces in the form of gravity force of wagon with cargo or without cargo―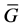and aerodynamic resistance force 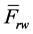(where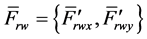) [8] .

We assume that in case of absence of the action of aerodynamic resistance force from the wagon side face (i.e. under 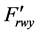= 0) truck wheel pairs roll without sliding during wagon movement before and outside braking positions (BP). According to Poinsot theorem taken from kinematics [5] , wheel pure rolling of a truck wheel pair (as moving centroid) down the rail threads (fixed centroid) accounts for the fact that their point of contact ( as contact of a circumference with a straight line) at the given time t₁, being their speed instant center (SIC) has the speed equal to zero.

Let us suppose that under changing climatic conditions during winter causing the change of air density followed by snow and hoarfrost, within bundle switching area and on sorting tracks, during wagon entrance on a side track through point switch, under the action of force 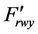and during wagon movement within braking positions wheel pairs roll down the rail threads with sliding.

We assume that during wagon passing along the length of hump and/or yard braking position (BP) truck wheel pairs move down the rail threads with sliding without rolling, but at the same time depending on the value of braking forces wheel sliding with rolling is not excluded.

4. Man-Made Assumption

Just as in [6] [7] we will consider the general case when the wagon is progressively rolling down the hump with a given initial speed 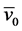(normally 4/5 km/h). While rolling down the hump the wagon will experience mainly the action of external forces in the form of gravity force of wagon with cargo or without cargo―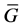and aerodynamic resistance force 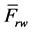(where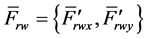) [8] .

We assume that in case of absence of the action of aerodynamic resistance force from the wagon side face (i.e. under 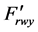= 0) truck wheel pairs roll without sliding during wagon movement before and outside braking positions (BP). According to Poinsot theorem taken from kinematics [5] , wheel pure rolling of a truck wheel pair (as moving centroid) down the rail threads (fixed centroid) accounts for the fact that their point of contact (as contact of a circumference with a straight line) at the given time t₁, being their speed instant center (SIC) has the speed equal to zero.

Let us suppose that under changing climatic conditions during winter causing the change of air density followed by snow and hoarfrost, within bundle switching area and on sorting tracks, during wagon entrance on a side track through point switch, under the action of force 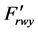and during wagon movement within braking positions wheel pairs roll down the rail threads with sliding.

We assume that during wagon passing along the length of hump and/or yard braking position (BP) truck wheel pairs move down the rail threads with sliding without rolling, but at the same time depending on the value of braking forces wheel sliding with rolling is not excluded.

5. Results of Analytical Solution Problems

As in [6] [7] , for the simplified computational model of wagon rolling down the hump taking into account rolling friction (pure rolling) we will take the model presented in Figure 1.

The forces of wagon (or a cut) wheel friction against the rail threads in the absence of defects in rolling bearings of box units come down to the forces of rolling friction the basic moment of which can be taken to be equal to M^(e) = f_rfF_z, where f_rf is a rolling friction coefficient, m; as this coefficient is equipotent to the arm of couple of rolling friction (wheel down the rail f_rf = 5 × 10⁻⁶, hardened steel on steel f_rf = 1 × 10⁻⁶); F_z is the sum of projections of all active forces onto the vertical axis falling at each box unit according to the technology of cargo mass center location in relation to axes of wagon crossing [6] :

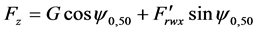. (1)

For the wheel pair of the wagon rolling down the hump up to the first braking position (1^st BP) due to the fact that there is always observed the condition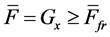, i.e. F > (f_fr/r_w)F_z (where G_x = Gsinψ_0,50 G_x = Gsinψ_0,50 is projection of gravity force of a wagon with cargo upon axis Ox, kN; r_w is wheel radius equal for a freight car to 0.475 m). Here the relation f_fr/r_w for the majority of materials is smaller than friction coefficient of sliding f. The value f between contacting wheel surfaces of freight cars and rail threads is taken to be 0.25 [2] . It is due to this difference (i.e.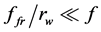) that there occurs the excess of forces ∆F_k,50 = Gsinψ_0,50 - F_fr causing wagon movement under its rolling down the hump with acceleration. An exception to this rule may be wet weather when coefficient f is reduced.

Hence, it is clear that rolling friction as the need arises can be replaced by symbolic sliding friction under pure rolling [6] [7] .

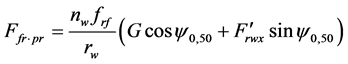, (1а)

where n_w is the number of wheels in trucks, item, (n_w = 8); f_rf is coefficient of rolling friction, m, as this coefficient is equipotent to the arm of couple of rolling friction (wheel down the rail f_fr = 5 × 10⁻⁶, hardened steel on steel f_fr = 1 × 10⁻⁶), r_w is wheel radius equal for a freight car 0.475 m.

On the mechanical system there also act internal forces in the form of rolling friction moments () and () in bearings of box units in leading truck A and rear truck B, at that M_трп = M_трпA + M_трпB.

In points of contact with rolling elements of inner diameter of bearing inner ring there emerge internal forces N_br―normal component of bearing reaction and in the same point on the rolling element from the inner ring there acts reaction N_b which is the same according to the module but opposite in direction. Here, just as above,

(i is the number of wheels in one truck axis (i = 2));

The moment of rolling friction in bearings of box units of leading and rear wagon trucks

(2)

where n_b = 8 is the number of box units in trucks, item; f_fr0 is coefficient of friction of rolling elements down bearing rings (normally taken to be 0.001 × 10⁻³), m; N_b is normal reaction falling on two cylindrical roller bearings, or the force acting upon the most loaded rolling element and determined according to the formula, kN [6] [7] :

(2а)

taking into account the fact that n_ffr is the total number of rolling elements, perceiving the load in each bearing, units; k is constant coefficient which is taken according to the row lane and type of rolling bearings.

By analogy, (1) rolling friction can be replaced by symbolic sliding friction under pure rolling motion of rolling elements in bearings [6] [7] :

, (2b)

where n_bb is the number of bearings in truck box units, item. (n_bb = 16); r_b is an outer radius of inner ring of roller bearing, m.

We rewrite the above formula taking into account (1a) and (2a):

. (3)

Joining (1) and (3) wheel rolling friction can be replaced by symbolic sliding friction under pure rolling and rolling elements in bearing box units:

,. (4)

where f₀ is some symbolic (or modified) coefficient of sliding friction:

. (4а)

In agreement with the above, all given constraint reaction are broken into normals, , , , , , and tangents, , , , , constituents the way it is presented in [9] .

In so doing, just as in [6] [7] allowance is made for the fact that, , ,;, , ,

.

It is also taken into account that the tangent constituents, , , , , , , , are forces of cohesion friction between contacting wheel surfaces and rail threads i.e., =, , , ,. Tangent constituent directed along the surface of rail threads is sliding friction force.

Introducing the notion of “shearing” and “retaining” forces, with allowance made for active and all reactive forces and in case of the impact of fair wind on the wagon we will get [6] :

;

.

The condition of wagon rolling down the first profile hump section with grades not steeper than 50% is

. (5)

This implies that the excess of forces, emerging on the first profile hump section is the motive power, the power that causes wagon rolling of the given gravity force G at speed v_e,50(t) and acceleration a₅₀ (t which depends mainly on the angle of rolling down the hump ψ_0,50 and to some extent on the coefficient of sliding friction of wheel flanges down the rail and also on the state of roller bearings in truck box units. So, in order to ensure wagon movement at the end of the first profile hump section at speed v_e,50(t) lower than the speed of entrance v_ewx(t) on the first braking position (1^st BP) i.e. v_e(t) < v_ewx(t), it is enough to select a rational value as a major geometrical hump parameter.

It is common knowledge that friction forces as resistance forces are always directed oppositely to the relative speed of wagon rolling down the hump. Friction force is a reactive (braking) force. In case of wagon (with cargo and/or without it) rolling down the hump friction force is a retaining force. That is why shunting masters consider this force to be “harmful” due to which the wagon (cut) may not reach the hump design point or, which is even worse, stop in the switching area impeding accelerated breaking up of the train. On the other hand, friction force as retaining force facilitates space-target regulation of cut speeds. This kind of speed regulation should be enough for switching operation and realization of design speeds of cuts at the exit from these positions. It is possible to provide cut approach to the yard braking position (3^rd BP) at speed not more than 23.4 km/h (6.5 m/s). In doing so the cuts should be able to roll up to the design point and the speed of cut collision in the yard shouldn’t exceed 5 km/h (1, 39 m/s).

It should be emphasized that while aiming at provision of space-target cut speed regulation it is necessary to slow down the wagon (or cut). At the same time it is necessary to slow down the rotation of wheels making them partially slide along the rail threads and at the expense of the emerging sliding friction between side surfaces of wheels and braking tires of wagon retarders due to the substantial value of compressed air maximum pressure in pneumo-system (0.75 MPa) it is possible to obtain considerable braking force. That is why the “desired” friction force in spite of generally accepted view shouldn’t be referred to incidental or “episodic” forces.

In a general case forces of sliding friction of wheels down the rails with rolling during wagon passing the length of hump (1^st BP, 2^nd BP) or yard braking position (3^rd BP) on mechanized humps:

, (6)

where F_τ is tangent component of constraint reaction (rail threads), which is equal according to Coulomb law F_τ = f_ск N with allowance made for the fact that f_sl is friction coefficient of wheel sliding along rail threads (metal against metal) f_sl = 0.15/0.25), N is normal component of constraint reaction which is modulo equal to the sum of projections of all active forces on the vertical axis falling on each box unit, F_z. It should be noted the value of f_sl also depends on weather conditions;

F_ffr = f_afF_af is friction force emerging between lateral surfaces of wheels and retarder braking bars where f_af = 0, 14/0, 20 is friction coefficient of sliding of wheel lateral surfaces against retarder brake beams [10] . It should be stressed that the value of f_af also depends on the weather conditions; F_af - is application force of retarder brake blocks to the wheel lateral surfaces or average load on the wagon axis (normally it is 90, 100, 140, 150 kN depending on the type of a retarder and air pressure) [11] . Here we are to bear in mind that force F_af is equipotent to retarder braking force F_br・f, i.e. f_afF_af = F_br・f. While solving practical problems it is possible to take

In that way, when a single wagon (or a cut) is within BP, in a general case the speed of the wagon is reduced (i.e. the wagon slows down) at the expense of sliding of skating surface of wheels in combination with their rolling down rail threads and also on account of sliding between wheel lateral surfaces and retarder brake bars. Special reference should be made to the fact that in BP zone because of application of brake bars through the fault of controller of train sorting speed (human factor) there may occur pure wheel sliding against brake bars until complete stopping of the wagon. In this case the value of F_тп is large as compared to F_τ (i.e. F_ffr > F_τ) and it is possible that = 0.

We rewrite the above expression for the case of wheel sliding against brake blocks with rolling in the form

.

Here the normal component N of constraint reaction modulo is equal to the sum of projections of all active forces on the vertical axis F_z, falling on each box unit. In accordance with this statement we form the above ratio in the following way:

, (7)

where is braking force which causes the movement of the wagon (or a cut) with slowdown; ψ_0,b is the angle of descend on the braking position of the hump section, rad.

Making allowance for the fact that each truck wheel enters hump the section of braking position consecutively, i.e. lagging in time τ, we rewrite [5] in the form:

(7а)

where σ₀(t), σ₀(t - τ₁), σ₀(t - τ₂) and σ₀(t - τ₃) σ₀(t), σ₀(t - τ₁), σ₀(t - τ₂) and σ₀(t - τ₃) are dimensionless retarded Heaviside functions which make it possible to present time t_i as one analytical expressions appropriate under any value of t in the interval,at that under; t is running time, s.; τ₁, τ₂ and τ₃ is the time lag of emerging of friction force while passing braking position by the second wheel of the leading truck (), the first () and the second wheel () of rear truck as compared with the first wheel of the leading truck (Figure 1), s:

;;

bearing in mind that l_tr and l_w is the half of the truck and wagon base, m; v is speed of entrance of the wagon onto the 1^st BP before the dividing switch, m/s (lower than 30.6 km/h (8.5 m/s) or 23.4 km/h (6.5 m/s) according to the design of retarders).

Analyzing the results of the previous reasoning we can write that the condition of wagon movement at the hump section braking positions with gradients 7/15‰ is (q.v. (5))

. (8)

Nonobservance of this condition (8) may lead to wagon stopping along the length of hump braking positions which may be the case in practice.

The analysis shows that excess of forces (i = I, II are the numbers of braking positions) emerging at hump section braking positions is the motive power making possible rolling of the wagon of prescribed gravity force G at speed v_ebi(t), and acceleration a_bi(t). These wagon kinematic parameters mainly depend on the gradient of hump braking positions ψ_0,bi, retarder braking force F_br・f., friction coefficient f_sl of sliding wheels against rail threads. It is necessary to ensure the movement of the wagon on hump sections with slowdown up to speed v_b(t) (considerably lower than entrance speed v_ewx(t), i.e.. This can be achieved not only by choosing the rational value of gradient ψ_0,b as a geometrical hump parameter but also by close controlling of braking force of wagon retarder F_br・f. In this case it is possible to ensure the movement of the wagon at speed v_ebi(t), which corresponds to acceleration with slowdown a₅₀(t), considerably lower in value than acceleration at the first profile hump section a₅₀(t), i.e..

Summing up the notion of friction force it is necessary to note that in addition to some other friction forces there are accidental or the so called “episodical” forces.

1) Friction forces of wheel flanges sliding along lateral sides of thrust rail. This kind of force appears during wheel rolling down the rail with sliding from the impact of transverse transferring inertia force I_ey and projections of aerodynamic resistance force on the lateral surfaces of wagon with cargo. Here it is assumed that wagon wheel flanges located from the side of the thrust rail are completely addressed to the thrust rail by forces I_ey and. According to the rule of reduction of forces these forces [4] , are reduced to the wheels of wheel pairs of the leading and rear trucks (or, i.e. and (Figure 2)

Figure 2 has the following symbols: is sum of forces I_ey and projection of force onto the transverse axis y (index W means that the forces act in the frontal plane); are transverse forces reduced to points and (point in Figure 1 is not shown); M_W is moment from pair of forces (which is applied in points and ), and (which is applied to the wagon lateral sides and/or cargo). In what follows the moment from pair of forces M_W will not be taken into account because it is not needed for solving the problem in question. It is should be remembered that moment M_W is necessary for solving problem on tilting of the wagon with cargo.

Force is found according to Coulomb law:

(9)

where f_rc・fr is reduced coefficient of sliding friction for freight cars (i.e. a symbolic value) [7]

. (9а)

Here F_z is a projection of all active forces onto the vertical axis falling on each box unit, kN (Figure 2); G_wp is gravity force of wagon wheel pair with account of rotation inertia, kN; f is friction coefficient of sliding between contacting surfaces of wheels and rail threads (for freight car it is taken to be 0.25); r_bi is rolling bearing inner radius in box units, m (0.079); r_w is wheel radius, for a freight car it is equal to 0.475.

2) Friction forces of sliding of wheels (with rolling) down the rail which emerge in winter conditions under the change of air density followed by snow and hoar frost within the limits of switching bundle zone and on sorting tracks. Here it is necessary to bear in mind that according to Coulomb law:

(10)

where f_cr is coefficient of resistance of the rail to the wheel movement (it is taken according to full-scale experiment data, or f_cr = f_sl (см. (6))), just as before, is a normal component

The condition of wagon movement on this hump section with gradient 0.6/2.5‰ is also

. (11)

It follows that excess of forces, emerging on hump section with gradients 0.6/2.5‰, is a motive force ensuring wagon rolling of prescribed gravity force G at speed v_ebi;0.6-2.5(t) and acceleration a_bi;0.6-2.5(t) (i just as previously are the numbers of braking positions). These wagon kinematic parameters mainly depend on the gradient of hump braking positions ψ_0,bi;0.6-2.5 and coefficient of resistance of the rail to the movement of wheels f_cr. At that the movement of the wagon is with slowdown at speed v_ebi;0.6-2.5(t) lower than the speed of exit from the braking positions v_bi(t), i.e.. This condition can be achieved only by choosing the rational value of tilt angle as a hump geometrical parameter as resistance coefficient of the rail to the wheel movement f_cr is an uncontrolled parameter, depending on weather conditions. In this case the wagon moves with slowdown a_bi;0.6-2.5(t) at speed v_ebi;0.6-2.5(t).

3) Friction force under wheel sliding without rolling (with account for momentary impact) resulting from the impact force (equipotent to the transverse transferring inertia force I_ey) directed crosswise the wagon (axis Oy) and appearing under striking of wheel pairs at switch points (against switch blades, frogs, guard rails) [2] . Here, we are to bear in mind that force is found according to the Coulomb law with allowance made for the sequence of contacting wheel flanges with point switch:

(12)

where f_fr・sl is coefficient of sliding friction (assumed to be pure sliding) of wheel flanges being struck about against rail threads (for wagon wheels it is taken to be f_fr・sl = 0.25); σ₀(t), σ₀(t - τ_1y), σ₀(t - τ_2y) и σ₀(t - τ_3y) - f_сп = 0.25); σ₀(t), σ₀(t - τ_1y), σ₀(t - τ_2y) and σ₀(t - τ_3y) - dimensionless Heaviside retarded functions defined just as in (7a) and differing by the fact that τ_1y, τ_2y and τ_3y is retardation time of emerging friction force while passing point switch of the second wheel of the leading truck (), the first wheel () and the second () wheel of the rear truck as compared with the first wheel of the leading truck (Figure 2), s.

The condition of wagon movement down point switch is

. (13)

Analyzing (13), special mention can be made of the fact that excess of forces, emerging at point switch sections is motive power causing wagon rolling of the designed gravity force G at speed v_e・mp(t) and acceleration a_mp(t). These kinematic parameters of the wagon depend mainly on the gradient, on which point switch ψ_0・mp = ψ_0,bII is located, and sliding friction coefficient of wheel flanges striking against rail threads f_mp. At that wagon movement down hump point switches is with slowdown speed v_e・mp(t) lower than the speed of wagon entrance onto the zone of switch bundles v_e・bII(t), i.e.. This condition can be achieved only by choosing a rational value of tilt angle ψ_0,mp as a hump geometrical parameter as sliding friction coefficient of wheel flanges striking against rail threads f_mp is an uncontrolled parameter depending on weather conditions. In this case there occurs wagon slowdown with acceleration a_mp(t), in value considerably lower than acceleration at section of braking positions with gradients 7/15‰ a_bi,7-15(t), 7/15‰ a_bi,7-15(t), i.e..

4) Sliding friction forces of wheels of the first wheel pair of the wagon leading truck (pure sliding*) in combination with rolling of the rest three wheel pairs of the wagon truck during wagon movement down hump tracks with the help of brake block.

Force is found according to the formula:

, (14)

where is symbolic sliding friction under pure rolling of wheels and elements in bearings of box units ((4) and (4a)):

, (15)

with allowance made for the fact that is some symbolic (or reduced) coefficient

. (15б)

Here n_wb is the number of wheels in trucks, item. (n_wb = 6); n_bb is the number of bearings in truck box units, units. (n_bb = 12);

is sliding friction force of the first wheel pair of the leading truck (at that one of the wheels is performing sliding with rolling while the other one together with the braking block is performing pure sliding):

, (16)

where f_slb is coefficient of sliding friction of wheels against the rail (“metal against metal”)

; N₁ = N/n_wb (here is just as previously, normal component of constraint reaction).

Putting (15) and (16) in (14) we will get:

,

or, taking into account the fact that N₁ = N/n_wb,

. (17)

Having regard to the fact that sorting yard tracks are designed with easy grades (1/1.5‰), for which cos(ψ_0;1-1.5) = 1 and sin(ψ_0;1-1.5) = 0,

, (17а)

where f_frb is coefficient of rolling friction of wheels with sliding in respect to the rail threads together with braking block under the wheels

(17б)

The condition of wagon movement down sorting yard track with gradients is 1/1.5‰

. (18)

Non-observance of this condition will result in wagon stopping at the prescribed length of the sorting yard track.

Hence it follows that excess of forces emerging at the hump sections with gradients 1/1.5‰, is the power causing wagon movement with acceleration a_1-1.5, which is, however, lower in value than acceleration at the sections of switching zone with gradients 1/2.5‰, i.e. a_ss < a_1-2.5. These kinematic parameters of the wagon mainly depend on the hump profile with gradients ψ_0,1-1.5 and coefficient of rolling friction of the wheels with sliding against rail threads together with braking block under the wheel f_frb. In so doing it is necessary to ensure the movement of the wagon in the hump yard as far as the group of standing wagons with slowdown at speed v_e,1-1.5 (t lower than the speed of exit of the wagon onto the zone of point switches v_e・bss(t), i.e.. These condition can be achieved not only by choosing the rational value of tilt angle ψ_0,ss, as a hump geometrical parameter, but also by choosing material of contacting surface of the wheel with braking block f_frb, as the coefficient of sliding friction of the other wheel of the wheel pair of the leading track against the other rail thread is an uncontrolled parameter. In this case there occurs slowdown of the wagon with acceleration a_1-1.5(t), considerably lower in value than acceleration at the sections of point switching with gradients 10/12‰ a_ss(t), i.e..

Summing up the results of the conducted analysis concerning the character of resistance (braking) forces due to which there occurs wagon (or cut) movement with slowdown it can be noted that for ensuring wagon rolling down the hump up to the moment of its stopping together with the group of standing wagons it is necessary to fulfill the conditions:;; and, which corresponds to adherence to inequalities;; and (q.v. (5), (8), (11), (13) and (18)).

Thus, there have been derived analytical formulas for determination of motive forces and resistance (braking) forces affecting the wheels of wheel pairs of the wagon during its rolling down hump longitudinal profile.

6. Conclusions

1) On the basis of classical statements of theoretical and applied mechanics, computable models of wagon rolling down the hump have been constructed and identified motive and resistance (braking) forces which will make it possible to model geometrical hump (parameters and kinematic characteristics of wagon movement).

2) Various conditions have been formulated, which makes it possible for a wagon to move down the hump profile elements allowing ensuring wagon (cut) slowdown in the process of movement from the hump crust down the design point of the sorting yard track.

The novelty of the derived analytical formulas of braking forces for each section of hump profile consists in correct account of all types of resistance affecting wagon movement. The obtained results of the research are a new stage in the development of this problem.

The significance of this methodology is presented by the opportunity of constructing a mathematical model of wagon rolling down the hump with allowance made for the influence of aerodynamic resistance due to the speed and direction.

In the long term the obtained results of the research can be used for solving technical problems of determination of hump rational geometrical parameters and wagon kinematic characteristics’ during its rolling.

Cite this paper

Khabibulla Turanov,Andrey Gordiienko, (2015) Analytical Determination of Conditions of Wagon Rolling Down Marshalling Hump Profiles. Open Access Library Journal,02,1-11. doi: 10.4236/oalib.1101912

References