Open Access Library Journal
Vol.02 No.09(2015), Article ID:68646,8 pages
10.4236/oalib.1101943
Body Mass Exponential Index: An Age-Independent Anthropometric Nutritional Assessment
Manuel Cidrás1,2
1Neonatal Unit, Hospital Universitario Virgen de la Arrixaca, Murcia, Spain
2School of Medicine, University of Murcia, Murcia, Spain
Email: mcidras@um.es
Copyright © 2015 by author and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 1 September 2015; accepted 18 September 2015; published 25 September 2015

ABSTRACT
Background: Body mass index (BMI) is a squared-height power function. Nevertheless, some studies show a significant exponential weight-height correlation. Objectives: To demonstrate that the weight-height relationship from 2 to 20 years of age is better expressed by an exponential function. Design: 5th, 50th and 85th percentile weight-height curves according CDC 2000 Growth Charts. A theoretical curve was created with the data on the 50th percentiles of weight and height for each age, equivalent to the 50th percentile of the weight-for-height curve. The statistical analysis was performed applying regression analysis of the curve estimation in the power and exponential models. Results: The exponential model correlation coefficient is higher than the power model. The exponential model variable (1.9 in boys, 2 in girls) was standardized to 2 to establish the body mass exponential index (BMEI): weight/exp(2*height). Weight-for-age and exponential height-for-age fiftieth percentile curves show a stable age-independent ratio near 2. These ratios are 1.5 and 2.5 for the 5th and 85th percentiles, respectively. The shape of the well-known curve BMI-for-age is due to the disparity between a exponential curve and a power curve. Conclusions: An exponential function expresses the weight-height relationship during growth better than a power function. A BMEI of 2 with limits of 1.5 and 2.5 is useful for screening nutritional status during growth, and the wei- ght-for-height chart is an ideal substitute for the BMI-for-age chart. The BMI-for-age curve shape and the disproportional BMI in taller children are mathematical artifacts without biological meanings.
Keywords:
Body Mass Index, Quetelet Index, Anthropometric Nutritional Status, Growth Rate, Weight-for-Height, BMI-for-Age
Subject Areas: Nutrition, Pediatrics

1. Introduction
The body mass index (BMI), named by Keys in 1972 [1] , is the standard screening for nutritional status, mainly for diagnosis [2] - [5] and for epidemiological follow-ups [6] - [8] of obesity. It is calculated by dividing the weight (W) by the square of the height (H) according to the ratio given by Quetelet in 1832 [9] [10] only for adults because, as stated in his publication, “during the development of the individuals of both sexes, we can consider the square of the weight, at different ages, as proportioned to the fifth power of their stature”. Simplified, this calculation is the weight divided by the height with an exponent of 2.5 [11] . This difference has not been considered, and since the year 1991 [2] [12] , the nutritional reference for childhood has been the BMI-for-age. The agreement for the normal limits in adults is between 18.5 and 25 kg/m2 [13] . Nevertheless, these limits are inapplicable to children, where the BMI varies according to age on a U shaped line, with the nadir at approximately 6 years of age, further complicated by the lack of consensus and the coexistence of the following four normal limits of BMI-for-age: 5th - 85th percentiles according to the CDC [14] , 18.5 - 25 BMI percentile lines at 18 years of age according to the IOTF [15] , ±2 SD according to the WHO [16] , and 80% - 120% of the 50th percentile according to others [17] .
The BMI has been criticized to the extreme of being considered an obsolete index that underestimates overweight [18] . The adiposity rebound of the BMI-for-age is considered a predictor of late obesity; however, it is unrelated to the moment of body fat increase [19] . An anthropometric study shows that taller children have a higher BMI and, thus, a higher probability of being diagnosed as obese [20] . Three limitations for the BMI have been described, namely, it depends on the height, on the leg length, and on the fat and non-fat weight [21] . Another distinctive fact is that the BMI-for-age curve lacks the marked increase in growth during the puberty growth spurt, a standard feature of the weight and height curves [22] .
The BMI is not a perfect measurement in children because it is height-dependent; however, it has been chosen due to its reproducibility and validity in easily measuring body fat [23] . Other options that have been unable to displace the BMI as a reference for the nutritional index include weight-for-height relationships such as the ponderal index (W/H3) [24] , the Benn index (W/Hp) [25] , or the (W-9)/H3.7 index [26] .
In a mathematical sense, the BMI is a specific case of the general power function model used to explain allometric growth [27] . Allometric growth was described by Huxley and Teissier in 1936 “to denote growth of a part at a different rate from that of body as a whole or of a standard”, and assumed that the power function represented this type of growth best [28] . However, Pasternak and Gianutsos propose that “if both organs (x and y) are exponential functions of time, the allometric relationship is power. If the organ y is exponential and the reference organ x is a linear function of time, the allometric relationship is exponential” [29] . Henneberg, in his anthropological study, also concluded that the exponential function showed a better representation of the weight- height relationship and presented the exponential W = 2・exp(2・H) equation [30] . The exponential weight-height relationship has also been demonstrated by other authors either directly [31] [32] or indirectly by applying the logarithm to the weight to obtain a lineal relationship with the height [33] .
The purpose of this study is to demonstrate that the weight-height growth relationship between 2 and 20 years of age is best expressed with an exponential function, enabling the creation of a more accurate nutritional index than the BMI. The study is performed by analyzing the data from the CDC 2000 growth chart [14] using a mathematical regression analysis of the curve estimation and a graphic analysis of the curves.
2. Methods
The CDC 2000 growth chart for children and teenagers from 2 to 20 years of age is available at the webpage cdc.gov/growthcharts and displays the weight-for-age, height-for-age, and BMI-for-age charts, as well as the weight-for-height chart between 77 and 121 cm, equivalent to the 2 to 5 years of age. The data were gathered from five national studies from 1963 to 1994 [14] .
The final curves represent the 3rd, 5th, 10th, 25th, 50th, 75th, 90th, 95th and 97th percentiles, distributed according to age and gender, as well as the 85th percentile in the BMI-for-age and weight-for-height charts. The 85th percentile of the weight-for-age distribution is not shown on the percentile tables and was calculated by applying the LMS method, as noted on the CDC webpage. The values are available for each month of age between month 24 and month 240, although this study used 6-month intervals to simplify calculations.
The weight-for-height curves exclude growth stages by being interrupted at 121.5 cm. To include all growth stages, a theoretical curve was created with the data on the 50th percentiles of weight and height for each age, equivalent to the 50th percentile of the weight-for-height curve.
The statistical analysis was performed using the SPSS version 20 statistical package by applying regression analysis of the curve estimation in the power and exponential models.
3. Results
The 50th percentile values of weight-for-age in relation to the 50th percentile of height-for-age formed an ascending curve, on which a regression analysis with a curve estimation of the two models, power and exponential, was performed. A significant weight-height relationship was obtained for these two models, but a stronger relationship was obtained for the exponential model (Table 1). In this first analysis, the age variable was not considered explicitly, although it was implicitly included because the W variable referred to the weight-for-age and the H variable to the height-for-age. A graphic analysis was presented by visually comparing the age-related curves.
Before plotting the charts, the equations were modified to match the power model with the BMI and the exponential model with Henneberg’s proposed equation [30] . This result was achieved by using a standard b1 value of 2 for all equations (Table 1). The modification was more significant for the power model because b1 value was 2.5; on the exponential model, a 1.9 value was changed only in males. The W/H2 ratio was the BMI, and the W/exp(2H) ratio was termed the body mass exponential index (BMEI).
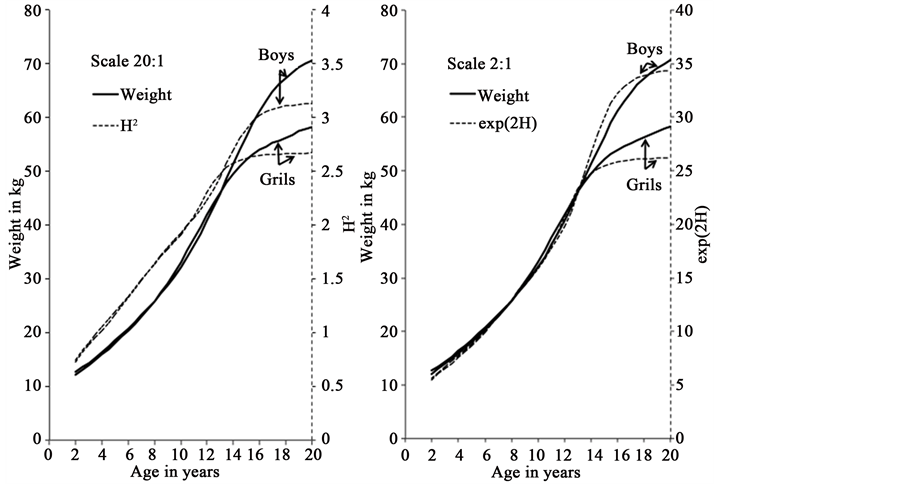
The subsequent step consisted of comparing the increases with age of W and the functions of H on the charts (Figure 1). The charts were plotted using two scales corresponding to the vertical axis, with the objective of maximizing overlap. The W and exp(2H) curves showed an important match on the 2:1 ratio. In contrast, between W and H2 curves the match was lower on the ratio 20:1.
The BMEI oscillates about a value of 2 (Figure 2). Two lines were added to this chart to represent the normal limits, constructed with the 5th and 85th percentiles over the 50th percentile of H. These lines are also wavy and close to the values 1.5 and 2.5, respectively. In both charts, a transiently high index is observed at the beginning of the pubertal growth spurt, at approximately 12 years of age in boys and 10 years of age in girls.
Finally, a theoretical recreation was performed to demonstrate the cause of the shape of the BMI. On a chart, with the values between 0.7 and 2 on the X-axis representing the height limits in the growth stage, two curves H2 and 2・exp(2H) were traced (Figure 3). The resulting curve from dividing H2/2・exp(2H) formed a similar BMI-for-age curve, with H = 1 as a minimum.
Figure 1. Comparison of weight between power and exponential curves. Comparison of 50th weight percentile with the H2 power (left) and the exp(2H) exponential (right) curves of the 50th height percentile, with corresponding scales.
Figure 2. Theoretical curves BMEI for age. Theoretical BMEI curves (W/exp(2H)) for age. The 50th percentile was used for height. For weight, the 50th, 5th, and 85th percentiles were used as BMEI central references and normal theoretical limits between 2 and 20 years of age for each gender.
Figure 3. Curve of exponential function divided by power function. The resulting curve after dividing the exponential curve by the power curve for the H values between 0.7 and 2. Upper chart, overlap of the exponential curve (continuous line) and power curve (discontinuous line). Lower chart, the result of dividing the two curves.
Table 1. Results of the curve estimation regression analysis in power and exponential models.
aThe equation was modified to isolate the constant and show the weight-height relationship. bThe variables (b1) were standardized to 2 to consider the BMI in the power model and an index according to the Henneberg equation [30] in the exponential model. H: height; W: weight.
4. Discussion
This study shows that the weight-height relationship from 2 to 20 years of age is better expressed by an exponential function than by a power function on which the BMI is based. The studied equation, W/exp(2H) is more accurate than any of the other equations, such as W/H2, W/H3, or W/Hp, in obtaining the nutritional index. The constant 2:1 proportionality between the weight and the exponential height (Figure 1) allows the value of 2, with limits of 1.5 and 2.5 equivalent to the 5th and 85th percentiles of weight-for-height, to be used as a fixed nutritional index without requiring a chart (Figure 2).
This study shows that the peculiar shape of the BMI-for-age chart is a mathematical anomaly. The initial descent observed until 6 years of age and the later ascent is due to a mathematical artifact imitated when dividing an exponential curve by a power curve (Figure 3). Thus, the theory of the prognosis of obesity in adults related to the early onset of the rebound BMI is meaningless [34] and is challenged by a recent study that rules out any relation between the adiposity rebound and body fat increase [19] . Another anomaly of the BMI is the disproportionate BMI in tall children [20] . The division of the exponential curve by the power curve can also explain this anomaly. As observed in Figure 3, the resulting curve increases more strongly in the higher values due to the exponential function.
Since Quetelet proposed the W/H2 coefficient [9] [10] , there has been persistence in using the height power function to create an anthropometric index of nutritional status. The cubic, however, seems to be a more logical option, as it considers the volume-equivalent body weight [35] ; nonetheless, the square power exhibits a better weight-height adjustment in adults. This same equation is used in children, even though Quetelet considered that the growth coefficient should be W2/H5 [9] [10] , equivalent to W/H2.5. This same value was obtained in this study (Table 1) and corresponds with the theory that the power should vary between 2 and 3 [35] . However, this debate may be considered unimportant because the adjustment of the exponential function is stronger than any power.
The exponential weight-height relationship has been previously suggested [29] - [31] without sufficient relevance for the scientific community to consider it as an alternative to the power relationship, perhaps due to the complexity of the equations and the anthropological or biological orientation in some studies. In 1961, Sargent [31] published the W = 2.6・exp(1.8H) equation represented in a semilogarithmic chart to be applied to children. In the year 1963 [32] , she published three-stage exponential equations for infancy, childhood, and adulthood in a semilogarithmic chart from 0.4 to 2 m. The equation for the infancy stage is W = 0.323・exp(4.71H), while in adults, the equations are gender-related, as W = 12.1・exp(H) for men and W = 9.5・exp(1.08H) for women. These studies have been further cited as a reference for the normal growth limits, but the exponential equations have been omitted. The exponential weight-height relationship during growth was also published by Henneberg in 1989 [30] with a pure anthropological approach and the proposal of a simpler equation, W = 2・exp(2H), that is used in this study. A paper by Pasternak and Gianutsos in 1969 [29] , although oriented to general biology, is also worth mentioning because they criticized the exclusive use of the power function as an explanation of allometric growth and suggested an exponential function as a more adequate approach when analyzing an exponential variable in relation to a lineal variable.
The exponential function is peculiar, as it doubles its value at regular intervals and can be demonstrated without needing mathematical tools such as logarithmic calculation or curve estimation. By example, the curve published by Leung et al. in 1996 [17] is a reference curve used in the Hong Kong Health Department that shows how the weight doubles at 35 cm height intervals in the exponential stage.
The supremacy of the BMI in nutritional assessment has cornered the weight-for-height charts. The studies comparing both methods show significant differences that endorse the use of the BMI-for-age as a better method [37] . However, this difference is an anomaly that results from dividing the exponential weight chart by the power squared height chart. The weight-for-height charts should be the gold standard of nutritional status on all growth stages and possibly for adults.
The use of the weight-for-height chart makes the weight-for-age chart obsolete, even inconvenient. This can be explained through the following example. Perrin et al., in their survey on the use of the BMI [38] , raise a hypothetical case of a 10-year-old girl of 130 cm of height (10th percentile) and 40 kg of weight (80th percentile), both within the normal percentiles, but overweight, as is only shown when observing that the BMI is over the 95th percentile. Overweight status is also shown directly on the weight-for-height chart (Figure 4) and by the BMEI of 2.97, which is greater than the normal limit of 2.5. Therefore, this result shows the obsolescence of the weight-for-age chart and the danger of considering a clearly pathological weight as normal. Another example that shows the superiority of the weight-for-height over the BMI-for-age chart is a forensic case by Davy-Jow et al. [39] , where the authors note that “The CDC website BMI Percentile Calculator for children would not return a weight-for-height centile because the figure was too far outside expected values” but can be diagnosed directly in the chart (Figure 4), as in the previous case, and with a BMEI of 1.37, which falls below the normal limit of 1.5.
The BMEI, suggested in this paper as an alternative for BMI, is more complicated to calculate, requiring a scientific calculator; but, this limitation may be considered attenuated, as it does not require a transfer to a chart.
Figure 4. Two examples of nutritional disorder. Weight-for-height in two nutritional disorder cases presented on a NCHS 1977 chart [40] . A girl 10 years of age who is 40 kg in weight and 130 cm in height [38] (black diamond) as an example of overweight and a girl 7 years of age who is 16.7 kg in weight and 125 cm in height [39] (black circle) as an example of underweight.
5. Conclusions
A nutritional index that associates the weight and height with an exponential function, such as the BMEI, is more accurate from 2 to 20 years of age than the BMI or other power function indexs. BMEI of 2, with limits of 1.5 and 2.5, could be used as nutritional index without requiring an age chart.
The BMI-for-age curve shape and the disproportional BMI in taller children are mathematical artifacts without biological meanings.
Acknowledgements
Author thanks Pedro Saavedra-Santana, PhD (School of Mathematics, University of Las Palmas de Gran Canaria), Gloria González-Azpeitia, PhD and Luis Peña-Quintana, PhD (Maternal and Child Hospital, University of Las Palmas de Gran Canaria) for their suggestions during the preparation of the manuscript. No financial compensation was provided to any of these individuals.
Funds for translation, manuscript editing services and meetings with experts in the area were provided by Nestlé Spain (Barcelona) and Laboratorios Ordesa (Barcelona).
The translation into English was performed by American Journal Experts.
Independent peer review prior to the submission process was performed by Rubriq.
Cite this paper
Manuel Cidrás, (2015) Body Mass Exponential Index: An Age-Independent Anthropometric Nutritional Assessment. Open Access Library Journal,02,1-8. doi: 10.4236/oalib.1101943
References
- 1. Keys, A., Fidanza, F., Karvonen, M.J., Kimura, N. and Taylor, H.L. (1972) Indices of Relative Weight and Obesity. Journal of Chronic Diseases, 25, 329-343.
http://dx.doi.org/10.1016/0021-9681(72)90027-6 - 2. Must, A., Dallal, G.E. and Dietz, W.H. (1991) Reference Data for Obesity: 85th and 95th Percentiles of Body Mass Index (wt/ht2) and Triceps Skinfold Thickness. The American Journal of Clinical Nutrition, 53, 839-846.
- 3. Klein, J.D., Sesselberg, T.S., Johnson, M.S., et al. (2010) Adoption of Body Mass Index Guidelines for Screening and Counseling in Pediatric Practice. Pediatrics, 125, 265-272.
http://dx.doi.org/10.1542/peds.2008-2985 - 4. Centers for Disease Control and Prevention (2014) Overweight and Obesity.
http://www.cdc.gov/obesity/adult/defining.html - 5. World Health Organization (2014) Obesity and Overweight. Fact Sheet No. 311.
http://www.who.int/mediacentre/factsheets/fs311/en/ - 6. James, W.P.T. and Lobstein, T. (2009) BMI Screening and Surveillance: An International Perspective. Pediatrics, 124, S42-S49.
http://dx.doi.org/10.1542/peds.2008-3586G - 7. Flegal, K.M., Kit, B.K., Orpana, H. and Graubard, B.I. (2013) Association of All-Cause Mortality with Overweight and Obesity Using Standard Body Mass Index Categories: A Systematic Review and Meta-Analysis. JAMA, 309, 71-82.
http://dx.doi.org/10.1001/jama.2012.113905 - 8. Ogden, C.L., Carroll, M.D., Kit, B.K. and Flegal, K.M. (2014) Prevalence of Childhood and Adult Obesity in the United States, 2011-2012. JAMA, 311, 806-814.
http://dx.doi.org/10.1001/jama.2014.732 - 9. Quetelet, L. (1832) Recherches sur le poids de l’homme aux different ages. Nouv Mem l’Academie R Des Sci B-Lett Bruxelles, t. VII.
- 10. Quetelet, L. (1994) A Treatise on Man and the Development of His Faculties. Obesity Research, 2, 72-85.
http://dx.doi.org/10.1002/j.1550-8528.1994.tb00047.x - 11. Burton, R.F. (2013) Adolphe Quetelet and the BMI: Fact, Fiction, and Childhood Growth. Obesity, 21, 6.
http://dx.doi.org/10.1002/oby.20036 - 12. Hammer, L.D., Kraemer, H.C., Wilson, D.M., Ritter, P.L. and Dornbusch, S.M. (1991) Standardized Percentile Curves of Body-Mass Index for Children and Adolescents. American Journal of Diseases of Children, 145, 259-263.
http://dx.doi.org/10.1001/archpedi.1991.02160030027015 - 13. WHO (2000) Obesity: Preventing and Managing the Global Epidemic. Report of a WHO Consultation, World Health Organization Technical Report, Series 894, I-XII, 1-253.
- 14. Ogden, C.L., Kuczmarski, R.J., Flegal, K.M., Mei, Z., Guo, S., Wei, R., Grummer-Strawn, L.M., Curtin, L.R., Roche, A.F. and Johnson, C.L. (2002) Centers for Disease Control and Prevention 2000 Growth Charts for the United States: Improvements to the 1977 National Center for Health Statistics Version. Pediatrics, 109, 45-60.
http://dx.doi.org/10.1542/peds.109.1.45 - 15. Cole, T.J., Flegal, K.M., Nicholls, D. and Jackson, A.A. (2007) Body Mass Index Cut Offs to Define Thinness in Children and Adolescents: International Survey. BMJ, 335, 194.
http://dx.doi.org/10.1136/bmj.39238.399444.55 - 16. De Onis, M., Onyango, A.W., Borghi, E., Siyam, A., Nishida, C. and Siekmann, J. (2007) Development of a WHO Growth Reference for School-Aged Children and Adolescents. Bulletin of the World Health Organization, 85, 660-667.
http://dx.doi.org/10.2471/BLT.07.043497 - 17. Leung, S.S., Lau, J.T., Tse, L.Y. and Oppenheimer, S.J. (1996) Weight-for-Age and Weight-for-Height References for Hong Kong Children from Birth to 18 Years. Journal of Paediatrics and Child Health, 32, 103-109.
http://dx.doi.org/10.1111/j.1440-1754.1996.tb00904.x - 18. Kragelund, C. and Omland, T. (2005) A Farewell to Body-Mass Index? The Lancet, 366, 1589-1591.
http://dx.doi.org/10.1016/S0140-6736(05)67642-8 - 19. Plachta-Danielzik, S., Bosy-Westphal, A., Kehden, B., et al. (2013) Adiposity Rebound Is Misclassified by BMI Rebound. European Journal of Clinical Nutrition, 67, 984-989.
http://dx.doi.org/10.1038/ejcn.2013.131 - 20. Franklin, M.F. (1999) Comparison of Weight and Height Relations in Boys from 4 Countries. American Journal of Clinical Nutrition, 70, 157S-162S.
- 21. Garn, S.M., Leonard, W.R. and Hawthorne, V.M. (1986) Three Limitations of the Body Mass Index. American Journal of Clinical Nutrition, 44, 996-997.
- 22. Krebs, N.F., Himes, J.H., Jacobson, D., Nicklas, T.A., Guilday, P. and Styne, D. (2007) Assessment of Child and Adolescent Overweight and Obesity. Pediatrics, 120, S193-S228.
http://dx.doi.org/10.1542/peds.2007-2329D - 23. Bellizzi, M.C. and Dietz, W.H. (1999) Workshop on Childhood Obesity: Summary of the Discussion. American Journal of Clinical Nutrition, 70, 173S-175S.
- 24. Burton, R.F. (2007) Why Is the Body Mass Index Calculated as Mass/Height2, Not as Mass/Height3? Annals of Human Biology, 34, 656-663.
http://dx.doi.org/10.1080/03014460701732962 - 25. Benn, R.T. (1971) Some Mathematical Properties of Weight-for-Height Indices Used as Measures of Adiposity. Journal of Epidemiology & Community Health, 25, 42-50.
http://dx.doi.org/10.1136/jech.25.1.42 - 26. Chinn, S., Rona, R.J., Gulliford, M.C. and Hammond, J. (1992) Weight-for-Height in Children Aged 4-12 Years. A New Index Compared to the Normalized Body Mass Index. European Journal of Clinical Nutrition, 46, 489-500.
- 27. Gayon, J. (2000) History of the Concept of Allometry. American Zoologist, 40, 748-758.
http://dx.doi.org/10.1668/0003-1569(2000)040[0748:HOTCOA]2.0.CO;2 - 28. Huxley, J. and Teissier, G. (1936) Terminology of Relative Growth. Nature, 137, 780-781.
http://dx.doi.org/10.1038/137780b0 - 29. Pasternack, B.S. and Gianutsos, R.R. (1969) Application of the Exponential and Power Functions to the Study of Allometric Growth, with Particular Reference to Doryline Ants. The American Naturalist, 103, 225-234.
http://dx.doi.org/10.1086/282597 - 30. Henneberg, M., Hugg, J. and Townsend, E.J. (1989) Body Weight/Height Relationship: Exponential Solution. American Journal of Human Biology, 1, 483-491.
http://dx.doi.org/10.1002/ajhb.1310010412 - 31. Sargent, D.W. (1961) An Evaluation of Basal Metabolic Data for Children and Youth in the United States. US Department of Agriculture, Home Economics Research Report No 14.
- 32. Sargent, D.W. (1963) Weight-Height Relationship of Young Men and Women. American Journal of Clinical Nutrition, 13, 318-325.
- 33. Newens, E.M. and Goldstein, H. (1972) Height, Weight, and the Assessment of Obesity in Children. British Journal of Preventive & Social Medicine, 26, 33-39.
http://dx.doi.org/10.1136/jech.26.1.33 - 34. Rolland-Cachera, M.F., Deheeger, M., Bellisle, F., Sempé, M., Guilloud-Bataille, M. and Patois, E. (1984) Adiposity Rebound in Children: A Simple Indicator for Predicting Obesity. American Journal of Clinical Nutrition, 39, 129-135.
- 35. Billewicz, W.Z., Kemsley, W.F. and Thomson, A.M. (1962) Indices of Adiposity. British Journal of Preventive & Social Medicine, 16, 183-188.
http://dx.doi.org/10.1136/jech.16.4.183 - 36. Fung, K.P., Lee, J., Lau, S.P., Chow, O.K., Wong, T.W. and Davis, D.P. (1990) Properties and Clinical Implications of Body Mass Indices. Archives of Disease in Childhood, 65, 516-519.
http://dx.doi.org/10.1136/adc.65.5.516 - 37. Flegal, K.M., Wei, R. and Ogden, C. (2002) Weight-for-Stature Compared with Body Mass Index-for-Age Growth Charts for the United States from the Centers for Disease Control and Prevention. American Journal of Clinical Nutrition, 75, 761-766.
- 38. Perrin, E.M., Flower, K.B. and Ammerman, A.S. (2004) Body Mass Index Charts: Useful Yet Underused. The Journal of Pediatrics, 144, 455-460.
http://dx.doi.org/10.1016/j.jpeds.2004.01.047 - 39. Davy-Jow, S.L., Lees, D.M.B. and Russell, S. (2013) Virtual Forensic Anthropology: Novel Applications of Anthropometry and Technology in a Child Death Case. Forensic Science International, 224, e7-e10.
http://dx.doi.org/10.1016/j.forsciint.2012.11.002 - 40. Hamill, P.V., Drizd, T.A., Johnson, C.L., Reed, R.B. and Roche, A.F. (1977) NCHS Growth Curves for Children Birth-18 Years: United States. Vital and Health Statistics, 11, 1-74.