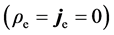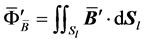Open Access Library Journal
Vol.02 No.09(2015), Article ID:68642,13 pages
10.4236/oalib.1101955
Magnetic Monopole Cannot Be Incorporated into the Dual Framework of Electromagnetic Theory
Qiankai Yao1,2
1School of Physics and Engineering, Zhengzhou University, Zhengzhou, China
2College of Science, Henan University of Technology, Zhengzhou, China
Email: yaoqk@zzu.edu.cn
Copyright © 2015 by author and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 2 September 2015; accepted 18 September 2015; published 23 September 2015

ABSTRACT
Through reexamining the intention of duality in classical physics, we will develop the electromagnetic field equations (EFEs) into a new dualized form. In the process, we will see 1) the dual symmetry does not represent the counterpart of electricity and magnetism, but a technique of expression, that is, any dualized equation will be equivalent to its originality. This symmetry can naturally lead to a conserved quantity (called the dual spin), and meanwhile is responsible for charge quantization; 2) magnetic monopole is not compatible with the classical physical laws. Such an opinion can be summarized as no-reality theorem, namely, any Dirac typical dual object will have no reality, such as, no realities of magnetic monopole and permanent electrics, so that the final conclusion is magnetic monopole which does not exist.
Keywords:
Magnetic Monopole, 5-D Field Equations, Dual Symmetry, Dual Spin
Subject Area: Theoretical Physics

1. Introduction
Regarding the originality of magnetic charge, we could go back to the 19th century. At that time Helmholtz used the concept to calculate the force exerted on a “magnetic particle” by electric current [1] . Meanwhile, based on the fact that the magnetic flux across a closed surface was always zero, Maxwell pointed out that no evidence indicated the possible existence of magnetic charge [2] . Nevertheless, a set of symmetrised MEs was first obtained by Heaviside in 1893 [3] , but Heaviside himself didn’t trust magnetic charge. Thus, he called it “fictitious”, and even thought that its sole worth was providing a convenient way to describe electromagnetic phenomena. In 1931, Dirac presented an idea of magnetic monopole to symmetrise Maxwell equations (MEs) as
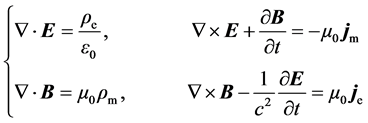 (1.1)
(1.1)
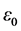 and
and 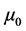 denote the dielectric permittivity and magnetic permeability. At the same time, Dirac also asserted that magnetic monopole would be responsible for the separate property of charge [4] . Importantly, Dirac’s idea could guide people to pursue the natural symmetry. This kind of symmetry is not only in mathematical form but also in physical connotation.
denote the dielectric permittivity and magnetic permeability. At the same time, Dirac also asserted that magnetic monopole would be responsible for the separate property of charge [4] . Importantly, Dirac’s idea could guide people to pursue the natural symmetry. This kind of symmetry is not only in mathematical form but also in physical connotation.
Essentially, what Dirac formulation led to was a Coulomb-like magnetic field with a flux going along a kind of unique string as a channel, but no actual magnetic monopole (at least no experiment could confirm its existence) [5] [6] . After all, breaking two poles (North and South) of a magnet always produced two smaller dipoles, rather than monopoles. Therefore, in Dirac theory, MEs have not really been symmetrised [6] - [8] . This is so- called magnetic monopole question.
Here, by the re-explanation of duality we will highlight that the duality doesn’t imply the existence of magnetic monopole, but a more extensive symmetry: MEs are not our only choice, whose dualized form will have the same effectiveness, and thus express the proper dual symmetry of electromagnetic movement. Finally, we will verify that magnetic monopole is impossible.
2. A General Form of Field Equations
In modern notation, MEs in Heaviside-Lorentz units read [4] [9]
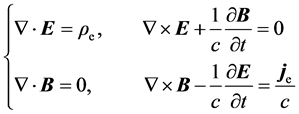 (2.1)
(2.1)
Applying this equation system in simple medium gives the following non-covariant form
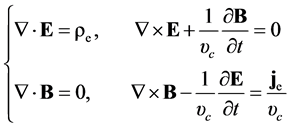 ,
,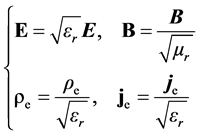 (2.2)
(2.2)
with a speed  defined by relative permittivity
defined by relative permittivity  and permeability
and permeability 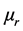 as
as
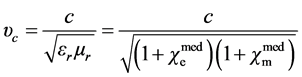 (2.3)
(2.3)
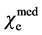 and
and  denote the electric and magnetic susceptibilities of medium.
denote the electric and magnetic susceptibilities of medium.
A set of covariant equations we want to introduce to replace Equation (2.2), is massive electromagnetic equations (described in Minkowski coordinate system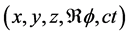 ) [10]
) [10]
 (2.4)
(2.4)
but need to redefine the polarized vector field 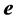 and scalar field
and scalar field 
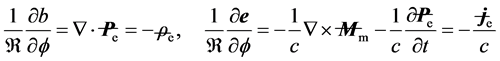 (2.5)
(2.5)
with
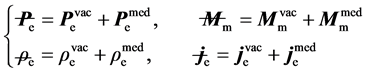
where, the characteristic length 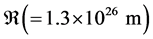
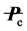
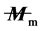
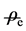
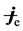
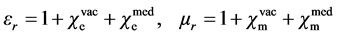
Now, if consider the charge fluctuation, we are allowed to write the flow equation
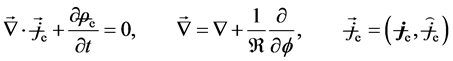
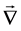
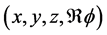
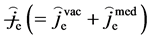
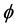
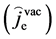
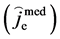
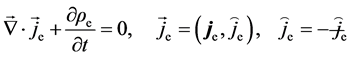
To illustrate (2.4) covariant, it is sufficient to show that the contained equations can be written entirely in terms of Lorentz tensors. The covariant path will begin with the introduction of electromagnetic field tensor
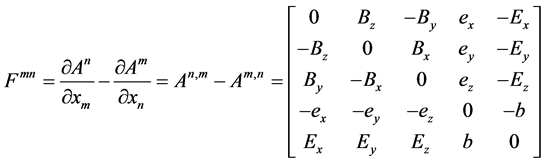
with a 5-dimensional potential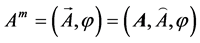
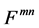
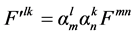
with transformation matrix
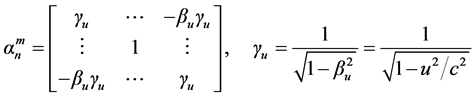
which reproduces the field transformation formulae
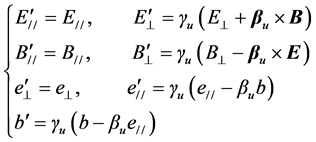
By
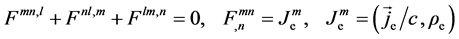
including the generalized continuity equation 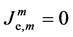
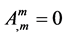
In the case of neglecting vacuum effect and added current (i.e.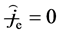
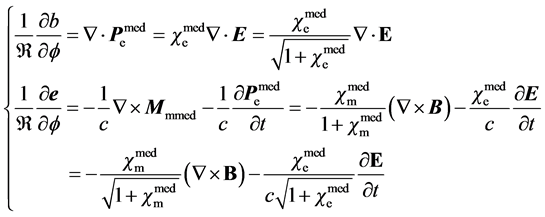
Substituting them into Equation (2.4), we find its first four equations (a) - (d) just reduce to Equation (2.2), implying the two are completely equivalent. Meanwhile, Equation (e) becomes the bounded charge conservation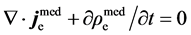
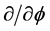
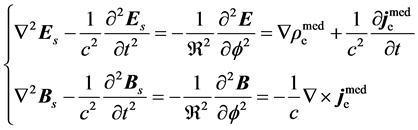
Correspondingly, the free part obeys
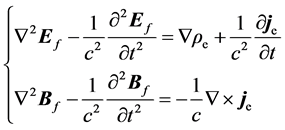
Pulsing (2.16) and (2.17) together gives
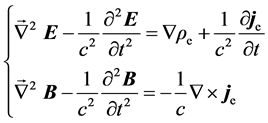
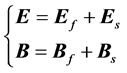
Which have the following free wave solutions
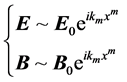
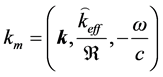
with an effective angular wave number 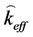
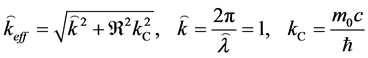
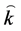
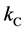
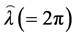
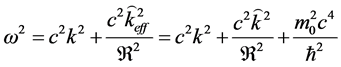
This dispersion relation can help us to get the group and phase velocities
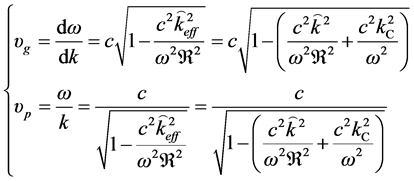
The former represents the project of generalized light speed c (propagating in space
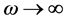
Especially, neglecting magnetization effect (due to 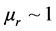
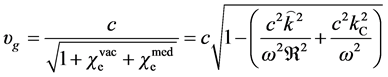
For vacuum case, the group velocity of photon becomes
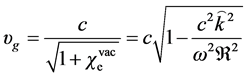
which can help us to estimate the vacuum susceptibility for the radiation of 
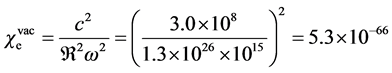
being a very small value. When traveling through a medium of refractive index
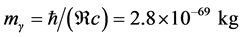
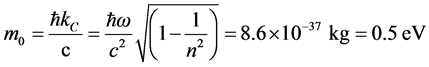
only about one-millionth of electron mass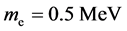
3. The Dualized Form of Field Equations
Notice that, by introducing the displacement current 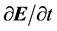
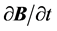
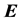
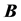
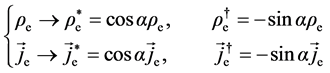
for dual current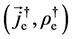
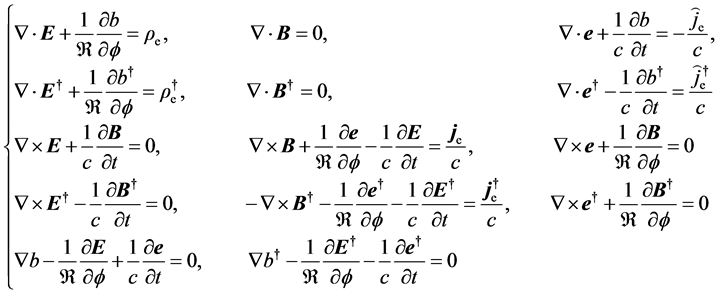
with the dual fields 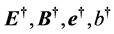
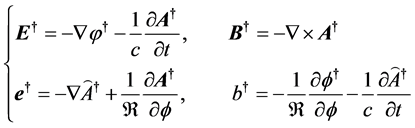
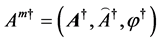
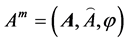
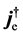
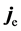
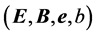
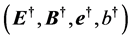
the here defined two groups of field quantities completely different from the original idea of duality, must be required to satisfy different equations: the former obeys the ones without superscript 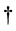
The dual symmetry of Equation (3.2) can be understood as invariance under dual transformation. Thus, by defining the 2-component arrays [11]
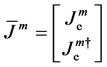
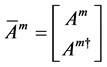
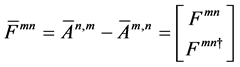
and a matrix
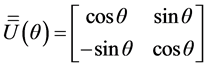
we have the transformation relation
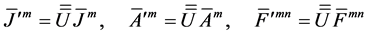
It shows that, the essence of dual transformation actually reflects a kind of rotation by angle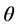
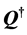
In the presented, the electromagnetic fields and their dual objects are treated in the same way, and there some consequences arise. For example, a moving dual charge 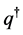
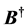
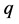
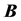
The dualized tensor 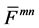
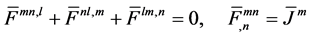
accompanied with the dualized continuity equation 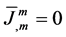
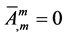
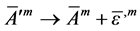
Figure 1. Dual transformation can be illustrated by the translation of dualized vector 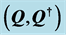

Figure 2. The fields induced by moving charged particles: (a) A pure electric charge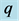
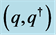
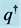
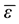
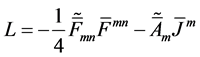
whose variation with respect to 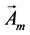
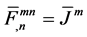
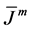
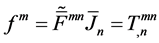
with the electromagnetic stress-energy tensor given by
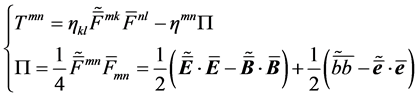
Applying dual transformation to Equation (3.10), we find
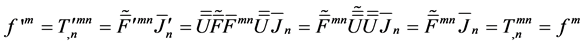
It shows that, the transformation doesn’t change the form of Equation (3.2), and the electromagnetic interaction also keeps the same. In this way, the electrodynamics displays its unique dual invariance. The invariance means, any one would obtain the same results, when he wish to adopt dualized equations to describe the electromagnetic phenomena.
It should be pointed that, due to dual symmetry, the ratio between two dual charges can be arbitrarily chosen, while the physical results will keep the same. So that we say, Equations (2.4) and (3.2) have the equivalent description efficacy; the only difference between them is that, the latter is understanding a charged particle as a dyon of carrying two mutual dual charges, rather than pure electric charge. In other words, regardless of whether an electron is a particle with unit negative charge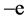
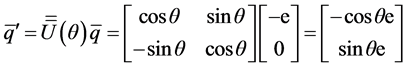
as long as assuming all particles in the universe have the same ratio
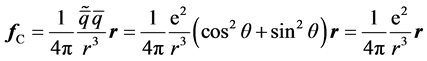
just equal to that between two conventional electrons. This means, Maxwell’s theory itself does not be short of symmetry, it can be dualized at any time. After all, we have no absolute reason to say, an electron only carries an unit negative charge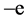
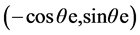
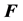
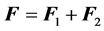
To examine the elements of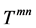
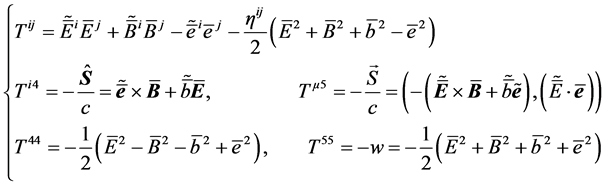
With this tensor in hand, it is straightforward to confirm that Equation (3.10) contains two conservation laws. The first is a statement of momentum conservation
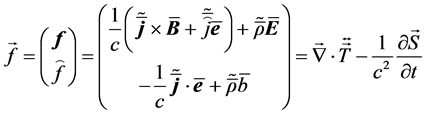
The second gives Poynting’s theorem of energy conservation
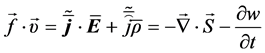
When no polarized fields 
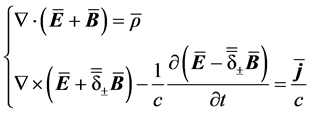
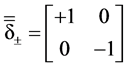
followed by a 4-force
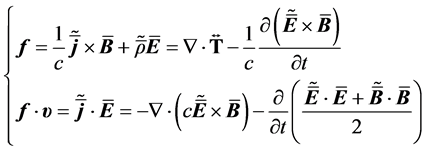
In absence of dual charge, we get back Maxwell theory.
4. Conserved Quantity and Charge Quantization
A celebrated theorem due to Noether makes a general connection: every invariance (or symmetry) of variable transformation would determine a conserved quantity [13] . What is the conserved quantity of dual transformation? It is the dual spin. So that, we focus our interest on the covariant electromagnetic action, and vary an action with the general form
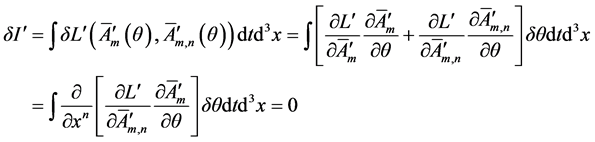
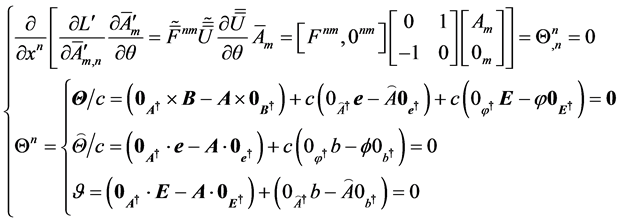
and hence, there be the following differential form
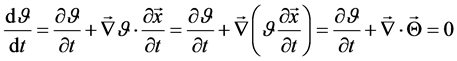
which provides a conserved quantity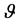
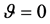
strict, this condition is nothing but the conversation form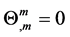
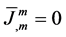
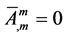
To demonstrate charge quantization, we look upon an electrically charged particle with 
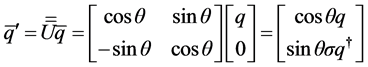
here, a proportional relation of 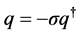
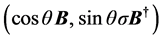
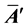
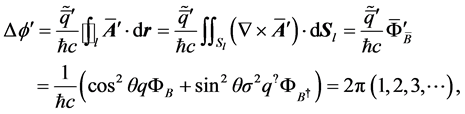
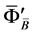
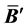
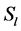
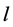
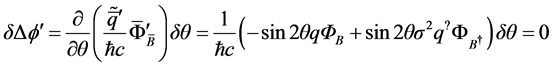
Then, based on the independency of two fluxes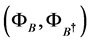
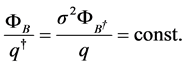
Due to the adjustability of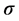
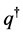
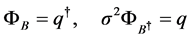
So that, putting the obtained into (4.5) gives the quantization relationship
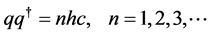
This derivation implies, not have to get help from Dirac monopole, the dual covariance would naturally lead to the charge quantization. In other words, the root of charge quantization is not at the existence of magnetic monopole, but the dual symmetry of electromagnetic movement.
5. Magnetic Monopole Does Not Exist
Right now, if suppose the dual object of electric charge were Dirac magnetic monopole (i.e.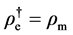
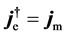
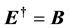
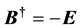
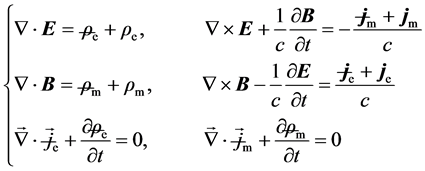
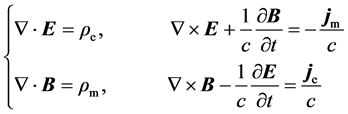
From which, we see that, the electric and magnetic quantities have been put in perfectly symmetrical position, and at present, there would be three kinds of way to produce magnetic field: magnetic charge, moving electric charge and changing electric field. So, the energy-momentum conservation for Maxwell-Dirac system needs to be derived from Equation (5.2), namely
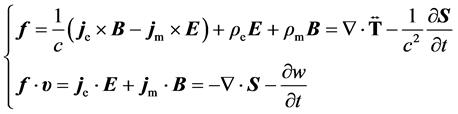
Just as our expectation, the electromagnetic energy-momentum changes into the mechanical form, in turn, the latter gets to balance by the former reducing. Ostensibly, it seems to imply, the law of energy-momentum conservation is still working well, and Maxwell-Dirac theory has no question, at least in mathematical form, not conflict with the classical physics. However, this is not the case; the involvement of magnetic monopole will completely change the trend of whole theory.
To illustrate this point, we suppose the existence of magnetic monopole, and conceive an electromagnetic system. As shown in Figure 3, the system is consisting of a permanent magnet and a magnetic circuit
Figure 3. An electromagnetic system is supposed to be composed of magnetic current 
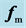
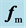
when there be a flux 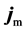
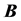
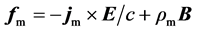
For unbounded space(modeled as a spherical volume tending to infinity), no momentum and energy in or out the closed boundary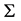
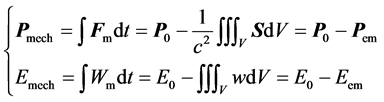
with the total magnetic force 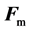
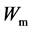
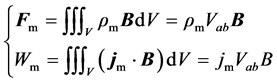
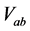
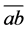
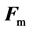
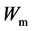
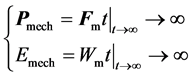
These results tell us that, the conceived system could unlimitedly transform its electromagnetic momentum and energy into the mechanical form, even like avalanche to an infinite negative value region(with imaginary fields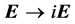
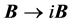
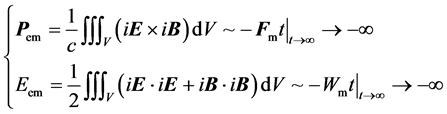
This is impossible by energy-momentum conservation. Therefore, as long as no physical experiment could detect the above transform, the assumption of that the magnetic monopole exists in universe cannot be true.
Hereby, it can be concluded that, the notion of magnetic monopole is not compatible with the classical physical laws. In other words, the magnetic field is not suitable to be understood as the dual target of electric one, since the magnetism is completely staying in an unequal position to electricity (see Table 1).
From the table we see that, any two supposed dual objects are actually antithetical each other, that is, if either is true (false), the other must be false (true). This situation can be stated as two equivalent statements:
1) There are no physical objects dual each other in Dirac mode, or any Dirac typical dual object has no reality (called no-reality theorem);
2) Any static vortex field is impossible to be an active one, or any field with source is impossible to possess simultaneously a static vortex structure (called no-vortex theorem).
Their equivalence can be proved by showing that if either is false, so is the other. Specifically, if the former were violated, namely magnetic monopole exist, magnetic field will become an active field. At the same time, the rotational magnetostatic field caused by permanent magnet also exists, and thus violates the second statement. In turn, the conclusion remains the same.
The key point is that, due to possessing a vortex structure, magnetic field lines do not begin or end in any volume of space(reflected completely by
In short, Maxwell theory itself does not require or forbid magnetic monopole exists, as well as the impossibility of perpetual mobile of the first kind states that, magnetic monopole has no reality. Although magnetic monopole has no reality, it still does not negate the usefulness of duality as a tool for studying the electromagnetic movement from a viewpoint of symmetry.
6. Conclusions
In conclusion, our acquisitions can be summed up as follows:
1) The developed 5-dimensional EFEs can provide us with a unified formalism; this formalism describing the medium effect by independent polarized fields has led to some meaningful results, such as the propagation and dispersion of light in matter;
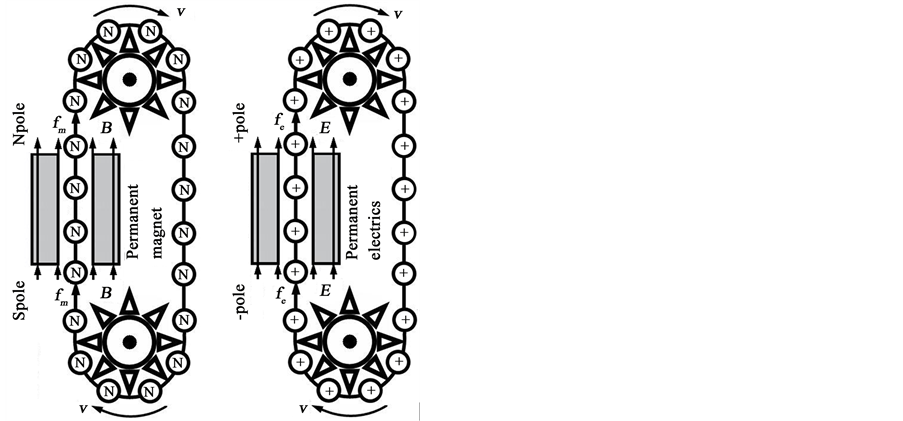
Figure 4. The existence of magnetic monopole or permanent electrics (the electric analog of permanent magnet) implies the feasibility of perpetual mobile of the first kind. Specifically, when moving through a rotational magnetostatic (a) (electrostatic (b)) field caused by permanent magnet (electrics), the magnetic (electric) charge system will work as a perpetual mobile of outputting the power unlimitedly. This is impossible.
Table 1. Some electromagnetic objects and their statuses (√ and × denote reality and no reality).
2) Due to possessing different natures, the electric and magnetic fields are not dual each other, whereas the dual quantities must be independent mutually. Based on the decision, we have developed EFEs into a 2-com- ponent dualized form. This form emphasizes that all the dualized equations should have the equivalent description efficacy to its originality. Especially, the dual spin of photon is essentially related to the electromagnetic dual symmetry, which also can provide us with a natural explanation for charge quantization;
3) Magnetic monopole is impossible, since it allows the electromagnetic energy-momentum to be transformed unlimitedly into the mechanical form. Crucially, the motivation of Dirac proposing magnetic monopole is to symmetrise MEs, but here it is no longer an indispensable concept. Eventually, Maxwell theory can be symmetrised at any time; it originally represents a particular form of 2-component dualized EFEs.
Cite this paper
Qiankai Yao, (2015) Magnetic Monopole Cannot Be Incorporated into the Dual Framework of Electromagnetic Theory. Open Access Library Journal,02,1-13. doi: 10.4236/oalib.1101955
References
- 1. Helmholtz, H.V. (1858) Ueber Integrale der hydrodynamischen Gleichungen, welche der Wirbelbewegung entsprechen. Journal für die reine und angewandte Mathematik, 55, 25. (In German)
- 2. Maxwell, J.C. (1865) A Dynamical Theory of the Electromagnetic Field. Philosophical Transactions of the Royal Society of London, 155, 459-512.
http://dx.doi.org/10.1098/rstl.1865.0008 - 3. Heaviside, O. (1893) Electromagnetic Theory. Chelsea Publishing Co., London.
- 4. Dirac, P.A.M. (1931) Quantized Singularities in the Electromagnetic Field. Proceedings of the Royal Society A, 133, 60.
http://dx.doi.org/10.1098/rspa.1931.0130 - 5. Dirac, P.A.M. (1948) The Theory of Magnetic Poles. Physical Review Letters, 74, 817.
http://dx.doi.org/10.1103/PhysRev.74.817 - 6. Preskill, J. (1984) Magnetic Monopoles. Annual Review of Nuclear and Particle Science, 34, 461-530.
http://dx.doi.org/10.1146/annurev.ns.34.120184.002333 - 7. Milton, K.A. (2006) Theoretical and Experimental Status of Magnetic Monopoles. Reports on Progress in Physics, 69, 1637.
http://dx.doi.org/10.1088/0034-4885/69/6/R02 - 8. Rajantie, A. (2012) Introduction to Magnetic Monopoles. Contemporary Physics, 53, 195-211.
- 9. Fryberger, D. (1985) Magnetic Monopole. IEEE Transactions on Magnetics, 21, 84-101.
http://dx.doi.org/10.1109/TMAG.1985.1063877 - 10. Yao, Q.K. (2015) The Unified Theoretical Form of Massive Electrodynamics. Open Access Library Journal, 2, e1372.
http://dx.doi.org/10.4236/oalib.1101732 - 11. Gonano, C.A. (2011) Estensione in N-D di prodotto vettore e rotore e loro applicazioni. M.S. Thesis. (In Italy)
https://www.politesi.polimi.it/bitstream/10589/34061/1/2011_12_Gonano.pdf, Dec. 2011. - 12. Schwinger, J. (1969) A Magnetic Model of Matter. Science, 165, 757-761.
http://dx.doi.org/10.1126/science.165.3895.757 - 13. Barut, A.O. (1964) Electrodynamics and Classical Field Theory of Fields and Particles. Macmillan, New York.