Open Access Library Journal
Vol.02 No.09(2015), Article ID:68639,16 pages
10.4236/oalib.1101715
Comparison between Modeling of Cetirizine Solubility Using Different Approaches: Semi-Empirical Density Based Correlations vs. Peng-Robinson EoS
Mostafa Lashkarbolooki, Ali Zeinolabedini Hezave*
Islamic Azad University, Dashtestan Branch, Borazjan, Iran
Email: *Zeinolabedinihezave.ali@gmail.com
Copyright © 2015 by authors and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 1 September 2015; accepted 16 September 2015; published 22 September 2015

ABSTRACT
The tunable nature of the solubility of various compounds, including molecules of pharmaceutical and biological interest, in supercritical fluids (SCFs) makes SCF extraction technology attractive for many separation and purification processes. Among the different influencing parameters, the most important one in the supercritical based processes is the knowledge of solubility of model solute. But, experimental measurement of the solubility of all pharmaceuticals in wide ranges of temperature and pressure is not only cost effective but also impossible in some cases. Regarding this fact, during the past decades, several approaches are proposed to model the solubility of the compounds in the supercritical fluids especially carbon dioxide. In this way, in the current investigation, two different approaches including five semi-empirical density based correlations (Mendez-Santiago and Teja (MST), Bartle et al., Chrastil, Kumar and Johnston (KJ) and Hezave et al.) and Peng-Robinson equation of state are used to find if it is possible to correlate the solubility of cetirizine with acceptable deviation as a function of temperature and pressure. The results reveal that among the examined approaches Hezave and Lashkarbolooki model leads to better overall correlative capability with average absolute relative deviation of 5.04% although Peng-Robinson EoS leads to lower AARD % of 3.85 % in 338 K isotherm.
Keywords:
Solubility, Supercritical Fluid, Cetirizine, Correlation, EoS, Semi-Empirical
Subject Areas: Medicinal Chemistry, Theoretical Chemistry, Thermochemistry

1. Introduction
Supercritical fluid (SCF) technologies have been gaining an increasing attention in different chemical processes during the past decades due to its applicable advantages. In this way, supercritical fluid (SCF) technology has been continuously developed for the processing of food, pharmaceuticals, and polymeric and specialty chemicals [1] .
SCFs are advantageous since they introduce desired properties of both liquids (good solvating strength) and gases (good diffusivity) make them a good alternative for conventional solvents. Among the different possible solvents for supercritical fluid technologies, carbon dioxide is most commonly used due to its mild critical pressure and temperature which make it a good candidate for processing of thermal labile compounds. In addition, carbon dioxide is non-toxic, green, available, cheap and non-toxic solvent. Also, since carbon dioxide introduces a mild critical condition, after expansion which occurs mostly into the ambient condition, it is vaporized from the matrix of the process material which remains no contamination. Due to this unique advantages, one of the most common applications of SCF technologies can be considered in pharmaceutical engineering for different applications such as drug delivery [1] [2] , extractions [3] [4] , purification [5] , solubilization [6] - [11] and crystal growth (particle size reduction and particle engineering) [12] - [20] .
Among the different parameters affecting the efficiency of the supercritical based technologies, solubility of pharmaceutical compounds is the major criterion for choosing appropriate process. In this way, several literatures reported the experimental measured solubility of different compounds as a function of temperature and pressure [5] - [11] . But the crucial point is that not only it is an expensive approach but also it is not possible to measure the solubility of all compounds in the supercritical carbon dioxide in wide ranges of temperature and pressure.
As a way out, during the past decades, different predictive approaches are proposed by different researchers to correlate the solubility of different compounds as a function of temperature and pressure as simply as possible [21] - [28] . Among the different predictive methods, Equations of State (EoS’s) are one of the first predictive methods applied to calculate the solubility of different compounds in SCFs at different temperatures and pressures and even at the presence of co-solvents. For example, Housaindokht and Bozorgmehr [29] have used different equations of state including Peng-Robinson (PR), Pazuki and others and a modified PR equation. Besides, they have used several mixing rules namely van der Waals 1 (VDW1), VDW2 and Adachi-Sugie. Undoubtedly, the most widely used model is cubic EoS’s from the VDW family, like PR, Soave-Redlich-Kwong (SRK) and Patel-Teja-Valderrama (PTV), together with several mixing and combining rules, like classical VDW mixing rules [30] . All EoS models require one or more temperature-dependent interaction parameters which must be correlated from experimental solubility data. With respect to this limitation, more complicated EoS models (e.g. statistical associating fluid theory (SAFT) [31] and mixing rules (e.g. Wong and Sandler [32] ) were developed which were difficult to be applied. Because of the large number of EoS’s and mixing rules available in the literature, researchers have to select the appropriate EoS and mixing rule for each system. But, in practice, each model cannot treat and reproduce effectively the solubility of all the compounds of interest. Besides, unfortunately, EoS based models require parameters such as critical constants and sublimation pressure of the complex pharmaceutical compounds, which are not always available experimentally.
Due to several limitations of EoS models, researchers proposed a new generation of predictive methods called semi-empirical density based correlations which used only the density of pure SCF and operational temperatures and pressures [21] [25] [26] [33] . Numerous studies were performed to investigate and predict the solubility of the systems SC-CO2-solutes using these semi-empirical equations. For example, Hojjati et al. [34] used six different equations to correlate the solubility data of three aromatase inhibitors finding the best fit with KJ’s model and Gordillo’s model. Later, those researchers determined the solubility of five statin compounds and correlated the experimental data with four semi-empirical equations [35] . They had reported that MST and Bartle models led to more accurate results. In addition, Sparks et al. [36] evaluated five density-based models with six solids and then developed a new model where the prediction of the solubility data was improved compared to other studied equations. After that, MST [33] fitted experimental data of 47 solids with two equations which led to accurate prediction of solubility data.
Regarding these progresses, it seems possible to use predictive tools for correlating solubility data and reduce the experimental measurement which consequently decreases the operational costs. In this way, in the current investigation, two different approaches including equation of sate (Peng-Robinson model) and semi-empirical density based correlations (including Mendez-Santiago and Teja (MST), Bartle et al., Chrastil, Kumar and Johnston (KJ) and Hezave and Lashkarbolooki) are used to compare their capability for correlating the solubility of cetirizine in supercritical carbon dioxide in wide range of temperature (308 - 338 K) and pressure (160 - 400 bar).
2. Modeling of Solubility Data
2.1. Semi-Empirical Correlation Method
The measured solubility data were correlated using four semi-empirical density-based correlations namely MST, KJ, Bartle et al. and Chrastil models. A brief description of the used correlations is given as follows. In the first stage, the Bartle et al. model [21] was used to correlate the solubility of fluvoxamine maleate. The general form of the Bartle et al. [21] model is as below:
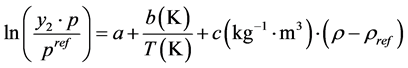 (1)
(1)
where a, b and c are fitting parameters, Pref, y and ρ are the reference pressure of 1 bar, the solute solubility and the density of carbon dioxide at a specific pressure and temperature modified by subtracting 700 kg∙m−3 considering as the reference density, ρref, respectively.
The second utilized model was Mendez Santiago and Teja (MST) which is one of the most popular one due to its accuracy and simplicity. In brief, MST has presented an empirical model based on the theory of infinitely dilute solutions [33] . An equation that follows a simple relationship for the solubility of solids in SCFs was deduced:
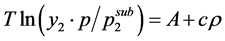 (2)
(2)
where T is the temperature, y2 is the solubility of the compound in terms of mole fraction, p is the pressure, 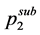 is the sublimation pressure of solid at temperature T,
is the sublimation pressure of solid at temperature T,  isthe density of the fluid, and A and c are constants independent of temperature.
isthe density of the fluid, and A and c are constants independent of temperature.
Since the sublimation pressures are not often available, the proposed model was combined with a Clausius-Clapeyron type expression for the sublimation pressure and a semi-empirical relation, with three adjustable parameters, for the solid solubility was derived:
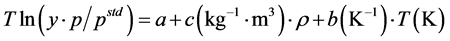 (3)
(3)
The adjustable parameters of the MST correlation including a, b, and c obtained by performing a simple graphical data fitting to  as a function of (
as a function of (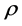 and T).
and T).
Finally, solubility data were correlated using Kumar and Johnston method (KJ) and Chrastil model (see Equations (4) and (5)).
 (4)
(4)
where y is the solubility of the solid, a, b and c are the fitting parameters and 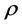 is the density of the supercritical fluid.
is the density of the supercritical fluid.
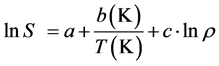 (5)
(5)
where, a, b and c are the fitting parameters and S is the solute solubility in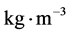 . Also, the b parameter can be utilized to estimate the solute heat of sublimation (ΔHsublimation= −Rb).
. Also, the b parameter can be utilized to estimate the solute heat of sublimation (ΔHsublimation= −Rb).
Among the above mentioned models, Chrastil method which is one of the oldest semi-empirical density-based correlations proposed in 1980s. This correlation was based on this assumption that the solute molecules surrounded by c molecules of a solvent form a solute-solvent complex. In other words, in the Chrastil model (Equation (5)), the fitting parameter c indicates the number of solvent molecules surrounding the solute molecule.
Finally, the correlation proposed by the authors [37] is used to compared wiuth the other predictive methods.
The proposed correlation was considered as a function of temperature, pressure and density of pure SC-CO2 (see Equation (6)) to not only into account the nature of the involved compounds but also to account the effects of system pressure and temperature on the solubility of the pharmaceutical in SC-CO2 [37] .
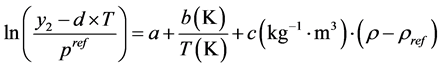 (6)
(6)
The optimization of the coefficient of the proposed correlation was obtained using a genetic algorithm. In the recent years, several computer-based methods for simulating and modeling of the different chemical phenomena have been proposed and examined [38] - [41] . Among the di®erent available predictive methods, genetic algorithms (GAs) are one of the widely used methods considered as a computational analogy of adaptive systems by John Holland in the 60 s [42] . GAs are modeled loosely on the principles of the evolution via natural selection, employing a population of individuals that undergo selection in the presence of variation-inducing operators such as mutation and recombination (crossover). A fitness function is used to evaluate individuals, and reproductive success varies with fitness. In other words, GAs are a way of solving problems by mimicking the processes mother nature uses based on the principles first laid down by Charles Darwin of survival of the fittest [43] [44] . In the light of its great fiexibility and capabilities, GA has been widely studied, experimented and applied in many fields in engineering worlds. Not only GAs provide alternative methods to solving problem, it consistently out-performs other traditional methods in most of the problems link. Many of the real world problems involved finding optimal parameters, which might introduce several difficulties to the traditional methods while the GAs can work willingly to find those optimal parameters. However, because of its outstanding performance in optimization, GAs have been wrongly regarded as an optimizer which is not fair enough [42] . By the way, due to the unique advantages of the GAs and its capability for optkmization of coefficients, it was used to find the optimum values of the Hezave and Lashakrbolooki [37] correlation.
2.2. Equation of State
As aforementioned, besides the semi-empirical correlations, Peng-Robinson EoS was used to model the measured solubility data. Regarding this purpose, the Peng-Robinson EoS coupled with conventional van der Waals mixing rule was used to evaluate the fugacity coefficient of solid in compressed fluid phase.
The solubility of a pure solid (component 2) in a supercritical fluid was estimated using the classical expression:
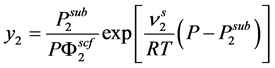 (7)
(7)
where, 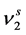 is the molar volume of the solid component 2,
is the molar volume of the solid component 2, 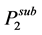 is the sublimation pressure of solute, T and P are the temperature and pressure of the system, respectively and
is the sublimation pressure of solute, T and P are the temperature and pressure of the system, respectively and 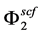 is the fugacity of the solid. In this work, the fugacity coefficient of solute in SC-CO2
is the fugacity of the solid. In this work, the fugacity coefficient of solute in SC-CO2 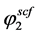 was calculated by means of using the Peng?Robinson EoS [45] combined with VDW1 mixing rule.
was calculated by means of using the Peng?Robinson EoS [45] combined with VDW1 mixing rule.
In addition, the lij and kij parameters were optimized using a differential evolution technique using MATLAB software. Differential evolution (DE) is a method optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. In brief, differential evolution is capable of handling non-differentiable, nonlinear and multimodal objective functions. It has been also used to train neural networks having real and constrained integer weights. This kind of solver works iteratively in which at each iteration, called a generation, new vectors are generated by the combination of vectors randomly chosen from the current population (mutation). The resultant vectors are then mixed with a predetermined target vector. This operation is called recombination and produces the trial vector. Finally, the trial vector is accepted for the next generation if and only if it yields a reduction in the value of the objective function. This last operator is referred to as a selection. This procedure continued until the desired error obtained.
3. Data Collection
In the current investigation, the solubility of cetirizine measured by the co-authors is gathered from the previously published literature [46] .
4. Results and Discussion
In the first stage of the current investigation, the solubility of cetirizine was correlated using Peng-Robinson EoS using VDW1 mixing rules as previously described. The two adjustable parameters (kij and lij) were optimized using the DE method using the following objective function:
where 

A closer examination in the listed results in Table 1 demonstrated that PR-EoS was not able to correlate the solubility of cetirizine in supercritical carbon dioxide willingly, although as the temperature increases the accuracy of the Peng-Robisnon EoS increases. The worst result of modeling was obtained for temperature of 308 K which is not far enough from the critical temperature of carbon dioxide (~304 K). In other words, this observed high AARD % for 308 K can be related to the transient behavior of the supercritical carbon dioxide at that temperature.
A closer examination of the listed results in Table 1 demonstrated that PR-EoS was not able to correlate the solubility of cetirizine in supercritical carbon dioxide willingly compared with the semi-empirical density based correlations.
Also, comparing the results obtained for Peng-Robinson EoS using two different mixing rules including VDW1 (see Table 1) and VDW2 (see Table 2) revealed that using VDW1 mixing rule leads to more accurate overall correlative capability of Peng-Robinson EoS.
In the second stage, five different semi-empirical density based correlations were used to find if it is possible to correlate the solubility if cetirizine with better accuracy compared with the results obtained by Peng-Robin- son EoS correlative approach (see Table 2). The results tabulated in Table 2 revealed that the overall results of the used correlations are better than Peng-Robinson EoS although Peng-Robinson EoS leads to more accurate results as the temperature increases. In addition, digging on the results listed in Table 2 revealed that these correlations are highly capable to correlate the solubility of cetirizine as a function of temperature and pressure. In more details, four of these correlations including Chrastil [26] , Bartle et al. [21] , MST [33] and KJ [25] models are rather the same while the proposed correlation by Hezave and Lashakrbolooki [37] leads to more accurate results of 5.03 % AARD (see Table 3, Figure 1 and Figure 2).
Besides the accurate correlative capability of the examined semi-empirical correlations, it is possible to extrapolate the solubility of cetirizine since the self-consistency test of these correlations leads to a straight line which means it is extrapolative capability of these correlations.
In details, as demonstrated in Figure 3, all of these correlations are able to satisfy the self-consistency test although it is completely clear that there is higher deviation among the measured solubility data and those correlated by these semi-empirical correlations when the temperature increases.
Table 1. The binary interaction parameters for cetirizine sc-CO2 system (VDW1 mixing rule).
Table 2. The binary interaction parameters for cetrizine-sc-CO2 system (VDW2 mixing rule).
Figure 1. The plotted experimental data and those obtained with the Chrastil model.
Figure 2. The plotted experimental data and those obtained with the Kumar and Johnston model.
Figure 3. Test of self-consistency for solubility of cetrizine in supercritical CO2 using the MST model.
Table 3. The obtained fitting constants for four density based correlations.
This observed trend can probably relate to the following fact that at the higher pressures which the density of compressed CO2 amounts to a value of 972.3 kg∙m−3 which is not so far away from water at ambient conditions can lead to a phenomenon called “squeezing out”. In other words, at higher pressure and liquid-like densities, the effect of “squeezing out”, that is a retrograde solubility, can often be observed leads to this fact that the density-based models do no longer work willingly in that regions. This phenomenon previously was reported by Kurnik and Reid [49] while further similar behavior was observed by Kraska et al. [50] for β-carotene solubility. They have been described this observed trend based on this fact that the deviation of the experimental data at pressures above 125 MPa can be due to a special isomerization occurred by an enrichment of cis-isomers in the solution while the all-trans β-carotene is squeezed out of the solution and crystallizes.
Finally, based on the obtained results it can be concluded that among the examined approaches, semi-empir- ical density based correlations are well able to satisfactorily correlate the solubility of cetirizine. In addition, among the examined semi-empirical density based correlations correlation proposed by Hezave and Lashakrbolooki correlate the solubility of cetirizine with acceptable level of accuracy with AARD % of 5.03%. At last, the worth mentioning point is that the semi-empirical density based correlations are not only able to well correlate the solubility of cetirizine in wide range of temperature and pressure but also they are able to extrapolate the solubility of compounds in supercritical carbon dioxide only as a function of temperature, pressure ans density of supercritical carbon dioxide which introduce them as an efficient tool for solubility interpolation and extrapolation.
5. Conclusions
In the current investigation, two different approaches were used and compared to find if it was possible to correlate the solubility of cetirizine as a function of temperature and pressure. In this way, one EoS namely Peng-Ro- binson Eos and five semi empirical density based correlations namely Mendez-Santiago and Teja (MST), Bartle et al., Chrastil, Kumar and Johnston (KJ) and Hezave and Lashkarbolooki were used and the obtained results were compared. The obtained result revealed that among the different predictive methods the semi-empirical density based correlations not only were easier to be used but also led to more accurate results compared with the Peng- Robinson EoS. In addition, the results of self-consistency test revealed that the semi-empirical density based correlations not only were able to correlate the solubility of cetirizine but also were able to extrapolate the solubility of the cetirizine. Finally, the results illustrated that among the different semi-empirical density based correlations, Hezave and Lashkarbolooki model led to more accurate results with minimum AARD % of 5.04%.
Finally, based on the obtained results one can conclude that although these predictive methods suffer from inaccuracies in some cases, it is possible to propose correlations which are able correlate the solubility of compounds in the supercritical carbon dioxide as a function of temperature and pressure with acceptable level of accuracy.
Cite this paper
Mostafa Lashkarbolooki,Ali Zeinolabedini Hezave, (2015) Comparison between Modeling of Cetirizine Solubility Using Different Approaches: Semi-Empirical Density Based Correlations vs. Peng-Robinson EoS. Open Access Library Journal,02,1-16. doi: 10.4236/oalib.1101715
References
- 1. Soares da Silva, M., Viveiros, R., Morgado, P.I., Aguiar-Ricardo, A., Correia, I.J. and Casimiro, T. (2011) Development of 2-(Dimethylamino)ethyl Methacrylate-Based Molecular Recognition Devices for Controlled Drug Delivery Using Supercritical Fluid Technology. International Journal of Pharmaceutics, 416, 61-68.
http://dx.doi.org/10.1016/j.ijpharm.2011.06.004 - 2. Rita, A., Duarte, C., Sousa Costa, M., Luísa Simplício, A., Margarida Cardoso, M. and Duarte, C.M.M. (2006) Preparation of Controlled Release Microspheres Using Supercritical Fluid Technology for Delivery of Anti-Inflammatory Drugs. International Journal of Pharmaceutics, 308, 168-174.
- 3. Papamichail, I., Louli, V. and Magoulas, K. (2000) Supercritical Fluid Extraction of Celery Seed Oil. Original Research Article. The Journal of Supercritical Fluids, 18, 213-226.
http://dx.doi.org/10.1016/S0896-8446(00)00066-8 - 4. Rajaei, H., Golchehreh, A.A., Zeinolabedini Hezave, A. and Esmaeilzadeh, F. (2013) Regeneration of Catalyst Clay Soils (Tonsil CO 610 G) by Supercritical Carbon Dioxide. Korean Journal of Chemical Engineering, 30, 842-851.
http://dx.doi.org/10.1007/s11814-013-0006-y - 5. Lee, Y.-N., Chen, C.-R., Yang, H.-L., Lin, C.-C. and Chang, C.-M.J. (2007) Isolation and Purification of 3,5-Diprenyl-4-hydroxycinnamic Acid (Artepillin C) in Brazilian Propolis by Supercritical Fluid Extractions. Separation and Purification Technology, 54, 130-138.
http://dx.doi.org/10.1016/j.seppur.2006.08.028 - 6. Esmaeilzadeh, F. and Goodarznia, I. (2005) Supercritical Extraction of Phenanthrene in the Crossover Region. Journal of Chemical & Engineering Data, 50, 49-51.
http://dx.doi.org/10.1021/je049872x - 7. Su, Ch.-Sh. and Chen, Y.-P. (2008) Measurement and Correlation for the Solid Solubility of Nonsteroidal Anti-Inflammatory Drugs (NSAIDs) in Supercritical Carbon Dioxide. The Journal of Supercritical Fluids, 43, 438-446.
http://dx.doi.org/10.1016/j.supflu.2007.08.006 - 8. Macnaughton, S.J., Kikic, I., Foster, N.R., Alessi, P., Cortesi, A. and Colombo, I. (1996) Solubility of Anti-Inflammatory Drugs in Supercritical Carbon Dioxide. Journal of Chemical & Engineering Data, 41, 1083-1086.
http://dx.doi.org/10.1021/je960103q - 9. Hezave, A.Z., Aftab, S. and Esmaeilzadeh, F. (2012) Solubility of Sulindac in the Supercritical Carbon Dioxide: Experimental and Modeling Approach. The Journal of Supercritical Fluids, 68, 39-44.
http://dx.doi.org/10.1016/j.supflu.2012.04.006 - 10. Hezave, A.Z., Khademi, M.H. and Esmaeilzadeh, F. (2012) Measurement and Modeling of Mefenamic Acid Solubility in Supercritical Carbon Dioxide. Fluid Phase Equilibria, 313, 140-147.
http://dx.doi.org/10.1016/j.fluid.2011.09.031 - 11. Hezave, A.Z. and Esmaeilzadeh, F. (2012) Solubility Measurement of Diclofenac Acid in the Supercritical CO2. Journal of Chemical & Engineering Data, 57, 1659-1664.
http://dx.doi.org/10.1021/je200012x - 12. Hezave, A.Z. and Esmaeilzadeh, F. (2012) Recrystallization of Micro Particles of Fenoprofen Using Rapid Expansion of Supercritical Solution. Journal of Dispersion Science and Technology, 33, 1106-1115.
http://dx.doi.org/10.1080/01932691.2011.599231 - 13. Hezave, A.Z. and Esmaeilzadeh, F. (2012) Precipitation of Micronized Piroxicam Particles via RESS. Journal of Dispersion Science and Technology, 33, 990-999.
http://dx.doi.org/10.1080/01932691.2011.590438 - 14. Hezave, A.Z. and Esmaeilzadeh, F. (2012) Fabrication of Micron Level Particles of Amoxicillin by Rapid Expansion of Supercritical Solution. Journal of Dispersion Science and Technology, 33, 1419-1428.
http://dx.doi.org/10.1080/01932691.2011.620883 - 15. Hezave, A.Z. and Esmaeilzadeh, F. (2010) Micronization of Drug Particles via RESS Process. The Journal of Supercritical Fluids, 52, 84-98.
http://dx.doi.org/10.1016/j.supflu.2009.09.006 - 16. Hezave, A.Z. and Esmaeilzadeh, F. (2010) Investigation of the Rapid Expansion of Supercritical Solution Parameters Effects on Size and Morphology of Cephalexin Particles. Journal of Aerosol Science, 41, 1090-1102.
http://dx.doi.org/10.1016/j.jaerosci.2010.08.004 - 17. Hezave, A.Z., Aftab, S. and Esmaeilzadeh, F. (2010) Micronization of Ketoprofen by the Rapid Expansion of Supercritical Solution Process. Journal of Aerosol Science, 41, 821-833.
http://dx.doi.org/10.1016/j.jaerosci.2010.01.006 - 18. Hezave, A.Z. and Esmaeilzadeh, F. (2010) Crystallization of Micro Particles of Sulindac Using Rapid Expansion of Supercritical Solution. Journal of Crystal Growth, 312, 3373-3383.
http://dx.doi.org/10.1016/j.jcrysgro.2010.07.033 - 19. Hezave, A.Z., Aftab, S. and Esmaeilzadeh, F. (2010) Micronization of Creatine Monohydrate via Rapid Expansion of Supercritical Solution RESS. The Journal of Supercritical Fluids, 55, 316-324.
http://dx.doi.org/10.1016/j.supflu.2010.05.009 - 20. Jung, J. and Perrut, M. (2001) Particle Design Using Supercritical Fluids: Literature and Patent Survey. The Journal of Supercritical Fluids, 20, 179-219.
http://dx.doi.org/10.1016/S0896-8446(01)00064-X - 21. Bartle, K.D., Clifford, A.A. and Jafar, S.A. (1991) Solubilities of Solids and Liquids of Low Volatility in Supercritical Carbon Dioxide. Journal of Physical and Chemical Reference Data, 20, 713-757.
http://dx.doi.org/10.1063/1.555893 - 22. Gordillo, M.D., Blanco, M.A., Molero, A. and de la Ossa, E.M. (1999) Solubility of the Antibiotic Penicillin G in Supercritical Carbon Dioxide. The Journal of Supercritical Fluids, 15, 183-190.
http://dx.doi.org/10.1016/S0896-8446(99)00008-X - 23. del Valle, J.M. and Aguilera, J.M. (1988) An Improved Equation for Predicting the Solubility of Vegetable Oils in Supercritical CO2. Industrial & Engineering Chemistry Research, 27, 1551-1553.
http://dx.doi.org/10.1021/ie00080a036 - 24. Adachi, Y., Lu, B.C.Y. and Sugie, H. (1983) Three Parameter Cubic Equations of State. Fluid Phase Equilibria, 13, 133-142.
http://dx.doi.org/10.1016/0378-3812(83)80087-9 - 25. Kumar, S. and Johnston, K.P. (1988) Modelling the Solubility of Solids in Supercritical Fluids with Density as the Independent Variable Supercrit. Fluids, 27, 1551-1553.
- 26. Chrastil, J. (1982) Solubility of Solids in Supercritical Gases. The Journal of Physical Chemistry, 86, 3016-3021.
http://dx.doi.org/10.1021/j100212a041 - 27. Sparks, D.L., Hernandez, R. and Estévez, L.A. (2008) Evaluation of Density-Based Models for the Solubility of Solids in Supercritical Carbon Dioxide and Formulation of a New Model. Chemical Engineering Science, 63, 4292-4301.
http://dx.doi.org/10.1016/j.ces.2008.05.031 - 28. Tabernero, A., del Valle, E.M.M. and Galan, M.A.A. (2010) A Comparison between Semiempirical Equations to Predict the Solubility of Pharmaceutical Compounds in Supercritical Carbon Dioxide. The Journal of Supercritical Fluids, 52, 161-174.
http://dx.doi.org/10.1016/j.supflu.2010.01.009 - 29. Housaindokht, M.R. and Bozorgmehr, M.R. (2008) Calculation of Solubility of Methimazole, Phenazopyridine and Propranolol in Supercritical Carbon Dioxide. The Journal of Supercritical Fluids, 43, 390-397.
http://dx.doi.org/10.1016/j.supflu.2007.07.013 - 30. Coimbra, P., Duarte, C.M.M. and de Sousa, H.C. (2006) Cubic Equation-of-State Correlation of the Solubility of Some Anti-Inflammatory Drugs in Supercritical Carbon Dioxide. Fluid Phase Equilibria, 239, 188-199.
http://dx.doi.org/10.1016/j.fluid.2005.11.028 - 31. Chapman, W.G., Gubbins, K.E., Jackson, G. and Radosz, M. (1989) SAFT: Equation of State Model for Associating Fluids. Fluid Phase Equilibria, 52, 31-38.
http://dx.doi.org/10.1016/0378-3812(89)80308-5 - 32. Wong, D.S.H. and Sandler, S.I. (1992) A Theoretically Correct Mixing Rule for Cubic Equations of State. AIChE Journal, 38, 671-680.
http://dx.doi.org/10.1002/aic.690380505 - 33. M’endez-Santiago, J. and Teja, A.S. (1999) The Solubility of Solids in Supercritical Fluids. Fluid Phase Equilibria, 158, 501-510.
http://dx.doi.org/10.1016/S0378-3812(99)00154-5 - 34. Hojjati, M., Vatanara, A., Yamini, Y., Moradi, M. and Najafabadi, A.R. (2009) Supercritical CO2 and Highly Selective Aromatase Inhibitors: Experimental Solubility and Empirical Correlation. The Journal of Supercritical Fluids, 50, 203-209.
http://dx.doi.org/10.1016/j.supflu.2009.06.015 - 35. Hojjati, M., Yamini, Y., Khajeh, M. and Vatanara, A. (2007) Solubility of Some Statin Drugs in Supercritical Carbon Dioxide and Representing the Solute Solubility Data with Several Density Based Correlations. The Journal of Supercritical Fluids, 41, 187-194.
http://dx.doi.org/10.1016/j.supflu.2006.10.006 - 36. Sparks, D.L., Hernandez, R. and Estevez, L.A. (2008) Evaluation of Density-Based Models for the Solubility of Solids in Supercritical Carbon Dioxide and Formulation a New Model. Chemical Engineering Science, 63, 4292-4301.
http://dx.doi.org/10.1016/j.ces.2008.05.031 - 37. Hezave, A.Z. and Lashkarbolooki, M. (2013) A New Simple Correlation for Calculating Solubility of Drugs in Supercritical Carbon Dioxide. Journal of Theoretical and Computational Chemistry, 12, Article ID: 1350062.
http://dx.doi.org/10.1142/S0219633613500624 - 38. Ghalami-Choobar, B., Ghiami-Shomami, A. and Nikparsa, P. (2012) Theoretical Calculation of pKb Values for Anilinies and Sulfonamide Drugs in Aqueous Solution. Journal of Theoretical and Computational Chemistry, 11, 283-295.
http://dx.doi.org/10.1142/S0219633612500307 - 39. Zhang, X., Han, X. and Xu, W. (2011) A Computer Simulation Study on Lewis Acid-Base Interactions and Cooperative and C-H Center Dot Center Dot Center Dot O Weak Hydrogen Bonding in Various CO2 Complexes. Journal of Theoretical and Computational Chemistry, 10, 483-508.
http://dx.doi.org/10.1142/S0219633611006591 - 40. Lashkarbolooki, M., Sadat Shafipour, Z., Zeinolabedini Hezave, A. and Farmani, H. (2013) Use of Artificial Neural Networks for Prediction of Phase Equilibria in the Binary System Containing Carbon Dioxide. The Journal of Supercritical Fluids, 75, 144-151.
http://dx.doi.org/10.1016/j.supflu.2012.12.032 - 41. Lashkarbolooki, M., Zeinolabedini Hezave, A. and Ayatollahi, S. (2012) Artificial Neural Network as an Applicable Tool to Predict the Binary Heat Capacity of Mixtures Containing Ionic Liquids. Original Research Article. Fluid Phase Equilibria, 324, 102-107.
http://dx.doi.org/10.1016/j.fluid.2012.03.015 - 42. http://www.doc.ic.ac.uk/-nd/surprise 96/journal/vol4/tcw2/report.html
- 43. http://www.cs.cmu.edu/Groups/AI/html/faqs/ai/genetic/part2/faq-doc-2.html
- 44. http://www.ai-junkie.com/ga/intro/gat1.html
- 45. Robinson, D.B. and Peng, D.Y. (1976) A New Two-Constant Equation of State Industrial and Engineering Chemistry: Fundamentals. Industrial & Engineering Chemistry Fundamentals, 15, 59-64.
http://dx.doi.org/10.1021/i160057a011 - 46. Hezave, A.Z., Mowla, A. and Esmaeilzadeh, F. (2011) Cetirizine Solubility in Supercritical CO2 at Different Pressures and Temperatures. The Journal of Supercritical Fluids, 58, 198-203.
http://dx.doi.org/10.1016/j.supflu.2011.05.017 - 47. Joback, K.G. and Reid, R.C. (1987) Estimation of Pure-Component Properties from Group-Contributions. Chemical Engineering Communications, 57, 233-243.
http://dx.doi.org/10.1080/00986448708960487 - 48. Constantinou, L. and Gani, R. (1994) New Group Contribution Method for Estimating Properties of Pure Compounds. AIChE Journal, 40, 1697-1710.
http://dx.doi.org/10.1002/aic.690401011 - 49. Kurnik, R.T. and Reid, R.C. (1981) Solubility Extrema in Solid-Liquid Equilibria. AIChE Journal, 27, 861-863.
http://dx.doi.org/10.1002/aic.690270528 - 50. Kraska, T., Leonhard, K.O., Tuma, D. and Schneider, G.M. (2002) Correlation of the Solubility of Low Volatile Organic Compounds in Near- and Supercritical Fluids. Part I: Applications to Adamantane and β-Carotene. The Journal of Supercritical Fluids, 23, 209-224.
http://dx.doi.org/10.1016/S0896-8446(02)00003-7
NOTES
*Corresponding author.







