Received 27 August 2015; accepted 12 September 2015; published 17 September 2015

ABSTRACT

In this article we have considered Fredholm integro-differential equation type second-order boundary value problems and proposed a rational difference method for numerical solution of the problems. The composite trapezoidal quadrature and non-standard difference method are used to convert Fredholm integro-differential equation into a system of equations. The numerical results in experiment on some model problems show the simplicity and efficiency of the method. Numerical results showed that the proposed method is convergent and at least second-order of accurate.

Keywords:

Composite Trapezoidal Method, Fredholm Integro-Differential Equations, Boundary Value Problem, Non-Linear Equation, Non-Standard Difference Method, Quadrature Formulas

Subject Areas: Numerical Mathematics, Ordinary Differential Equation

1. Introduction

The occurrences of differential equations and integral equations are common in many areas of studies in particular sciences and engineering. However, there are many mathematical formulations in science where both differential and integral operators appear together in the same equation. These equations were termed as integro-dif- ferential equations. The integro-differential equations have gained importance in the literature for the variety of their applications and in general it is impossible to obtain solutions of these problems using analytical methods. So it is required to obtain an efficient approximate solution. There are different methods and approaches for approximate numerical solution such as difference and compact finite difference method [1] - [3] , Tau method [4] , an extrapolation method [5] , Taylor series method [6] , method of regularization [7] [8] , variational method [9] , adomian decomposition method [10] , variational iterations method [11] and references therein.

In this article we consider a method for the numerical solution of the following linear Fredholm integro-dif- ferrential equations of the form

(1)

subject to the boundary conditions

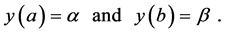
where and are real constant. The functions 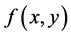and the kernel are known. The solution 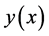is to be determined.

The emphasis in this article will be on the development of an efficient numerical method to deal with approximate numerical solution of the integro-differential equation and then to prove theoretical concepts of convergence and existence. The theorems of uniqueness, existence and convergence are important and can be found in the literature [1] [12] [13] . The specific assumption to ensure existence and uniqueness of the solution to problem (1) will not be considered. Thus the existence and uniqueness of the solution to problem (1) are assumed. We further assumed that problem (1) is well posed.

Last few decades have seen substantial progress in the development of approximate solution by non-conven- tional methods. One such method, a non-standard finite difference method has increasingly been recognized as a efficient method for the numerical solution of initial value problems in ordinary differential equation [14] - [16] . The non-standard finite difference method is simple and generates impressive numerical result with high accuracy. Hence, the purpose of this article is to develop a non-standard finite difference method similar to [16] for numerical solution of the second-order boundary value problems of Fredholm integro-differential Equation (1).

We have presented our work in this article as follows. In the next section we derived a non-standard finite difference method. In Section 3, we have discussed local truncation error in propose method and convergence under appropriate condition in Section 4. The applications of the proposed method to the model problems and illustrative numerical results have been produced to show the efficiency in Section 5. Discussion and conclusion on the performance of the new method are presented in Section 6.

2. The Non-Standard Finite Difference Method

Let us assume that is smooth and separable kernel otherwise by using the Taylor series expansion for the kernel, reduce it to separable kernel. Let further assume that 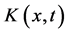is bounded by for at all points of i.e..

We define N finite nodal points of the domain [a, b], in which the solution of the problem (1) is desired, as using uniform step length h such that. Suppose that we wish to determine the numerical approximation of the theoretical solution of the problem (1) at the nodal point. We denote the numerical approximation of 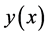at node as. Let us denote as the approximation of the theoretical value of the source function at node. Thus the integro-differential Equation (1) at node may be written as

(2)

where.

We approximate the integral that appeared in Equation (2) by the repeated/composite trapezoidal quadrature method [17] which will yield the following

(3)

where using uniform step length h such that , is the truncation error in interval and quadrature nodes are numerical coefficients such that

and do not depend on the function. The term in (3) depends on N and large N reduces considerably. Let us define a function node after neglecting the error terms in (3) such that

(4)

Thus with the application of (4), the considered problem (1) at node may be written as,

(5)

subject to the given boundary conditions.

Let us assume a local assumption as in [18] that no truncation errors have been made i.e.

and following the ideas [19] , we propose non-standard finite difference method for the approximation of the analytical solution of the problem (5) at node as,

(6)

where. Thus we will obtain the system of nonlinear equations at each nodal point

For the computational purpose in Section 4, we have used the following finite difference approximation in place of in (6),

(7)

Thus from (7) we can write (6) as,

(8)

which is a nonlinear system of equations. We have to solve a nonlinear system with a large number of equations. So there is some complexity in the system and computation is difficult. However we have applied an iterative method to solve above system of nonlinear Equation (8).

3. Local Truncation Error

The local truncation error at the node using the exact arithmetic, is given as:

At the nodal point, , the truncation error in Method (5) may be written [17] ,

writing the Taylor series expansion for at nodal point and binomial expansion under appropriate conditions for above equation. Simplify the expression so obtained by using and we have following expression

(9)

Thus we obtain a truncation error at each node of.

4. Convergence of the Non-Standard Difference Method

Consider the difference Method (6),

Let us ignore the third and other terms on right side of the above expression. After replacing by the second order difference approximation, we have

Thus

(10)

Let us define

So we can write (10) as,

(11)

Let us define

Let us define column matrix and as

The difference Method (11) represents a system of nonlinear equations in unknown Let us write (11) in matrix form as,

(12)

where

is tridiagonal matrix. Let Y be the exact solution of (11), so it will satisfy matrix equation

(13)

where Y is column matrix of order which can be obtained replacing y by Y in matrix y and T is truncation error matrix in which each element has.

Let us define

After linearization of, we have

where. Let us define Thus we have

(14)

Similarly, we can linearize, and obtained the following results :

(15)

(16)

By Taylor series expansion of. about, and from (14)-(16), we can write

(17)

where is a tri-diagonal matrix defined as

Let us assume that the solution of difference Equation (11) has no round off error. So from (12), (13) and (17) we have

(18)

Let us define

Then

We further define.

Let there exist some positive constant such that. So it is possible for very small,

Let, denotes the row sum of the matrix where

Neglecting the higher order terms i.e. in then it is easy to see that is irreducible [20] . Also by row sum criterion matrix is for sufficiently small h monotone [21] . For the bound of, we define [22] - [24] ,

where

It is easy to prove after neglecting higher order terms i.e. in the above expressions that matrix is diagonally dominant. Thus matrix is nonsingular [25] i.e. exist and [21] . Let and

Then

(19)

Thus from (18) and (19), we have

(20)

It follows from (9) and (20) that as. Thus we conclude that Method (6) converges and the order of the convergence of Method (6) is at least quadratic.

5. Numerical Experiments

To illustrate our method and demonstrate its computational efficiency, we have considered four model problems. In each model problem, we took uniform step size h. In Tables 1-4, we have shown MAY the maximum absolute error in the solution y of the problems (1) for different values of N. We have used the following formula in computation of MAY,

The order of convergence of the Method (8) is estimated by the formula

where m can be estimated by considering the ratio of different values of N.

We use Newton-Raphson iteration method to solve the system of nonlinear equations arising from Equation (9). All computations are performed on a Windows 2007 Ultimate operating system in the GNU FORTRAN environment version 99 compiler (2.95 of gcc) on Intel Core i3-2330M, 2.20 Ghz PC. The solutions are computed on N nodes and iteration is continued until either the maximum difference between two successive iterates is less than 10⁻¹⁰ or the number of iterations reaches 10³.

Problem 1. The model linear problem given by

subject to boundary conditions

where is calculated so that the analytical solution of the problem is. The MAY computed by Method (8) for different values of N and no. of iterations Iter. are presented in Table 1.

Problem 2. The model linear problem given by

subject to boundary conditions

The analytical solution is. The MAY computed by Method (8) for different values of N and number of iterations Iter. are presented in Table 2.

Problem 3. The model nonlinear problem [26] given by

subject to boundary conditions

The analytical solution is. The MAY computed by Method (8) for different values of N and number of iterations Iter. are presented in Table 3.

Problem 4. The model nonlinear problem given by

subject to boundary conditions

where is calculated so that the analytical solution of the problem is. The MAY computed by Method (8) for different values of N and number of iterations Iter. are presented in Table 4.

We have described a numerical method for numerical solution of Fredholm integro-differential type boundary value problem and four model problems considered to illustrate the preciseness and effectiveness of the proposed method. Numerical results for example 1 which is presented in Table 1, for different values of N show decreases with step size maximum absolute errors in our method decrease. Similar observation can be found in result of example 2, 3 and 4. Over all Method (6) is convergent and convergence of the method does not depends on choice of step size h.

6. Conclusion

A non-standard difference method to find the numerical solution of Fredholm integro-differential equation type boundary value problems has been developed. This method has been used for transforming Fredholm integro- differential equation into system of algebraic equations i.e. each nodal point We will obtain a system of algebraic equations given by (6). So we have obtained a nonlinear system of equations that is always difficult to be solved, which is the disadvantage of the proposed method. The proposed method produces good approximate numerical value of the solution for variety of model problems with uniform step size. The numerical results for the model problems showed that the proposed method is computationally efficient. The rate of convergence of the present method is quadratic. The idea presented in this article leads to the possibility to develop non-standard difference methods for the numerical solution of higher-order integro-differential equations. Works in these directions are in progress.

Cite this paper

Pramod Kumar Pandey, (2015) Non-Standard Difference Method for Numerical Solution of Linear Fredholm Integro-Differential Type Two-Point Boundary Value Problems. Open Access Library Journal,02,1-10. doi: 10.4236/oalib.1101465

References