Open Access Library Journal
Vol.02 No.09(2015), Article ID:68591,5 pages
10.4236/oalib.1101838
An Improved “Interference Collapse Rule” of Quantum Mechanics
Hans H. Diel
Diel Software Beratung und Entwicklung, Sindelfingen, Germany
Email: diel@netic.de
Copyright © 2015 by author and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 10 August 2015; accepted 27 August 2015; published 2 September 2015

ABSTRACT
The double-slit (gedanken-) experiment is the most famous experiment in quantum theory (QT). The explanation of the strange behavior of the electron in this experiment is used as a key example in QT in general. The description of the experiment includes a rationalization of when in quantum mechanics interference occurs and (most importantly) when it “collapses”. The aforementioned rule, here called the “interference collapse rule”, is contained in almost all textbooks of QT with only slight variations. However, this rule makes sense only with additional assumptions which apparently are not generally agreed upon among physicists. The paper proposes an improved interference collapse rule that connects the interference collapse to the QT measurement and a functional interpretation of QT measurement.
Keywords:
Double-Slit Experiment, Measurement Problem, Interference
Subject Areas: Modern Physics

1. Introduction
When the author began the development of his computer model of quantum theory (QT) (see [1] ), with the goal of supporting the simulation of the major QT (gedanken-) experiments, the double-slit experiment (see section 2) was one of the first samples whose modeling was attempted. Soon it was realized that the double-slit experiment cannot be supported by a computer model, at least if the canonical interpretation of the double-slit experiment presented in QT textbooks was used. It turned out that the source of the problem was neither the indeterminism of QT (it is easy to simulate indeterminism), nor the often-mentioned strangeness of QT. The problem was that the typical explanation of the double-slit experiment and the rule for when the interference occurs and when it “collapses” is given in terms of objects and conditions which can neither be transformed to proper mathematics, nor can it be mapped to a facts-driven decision algorithm.
When the author discussed the problem with physicists, his problem was not properly acknowledged. He instead was presented with interpretations and rephrasings of the standard textbook formulations which did not substantially help to solve the issue (from the author’s perspective). Typically, the attempts to generate an improved formulation included assumptions that were pretended implied by the original standard formulation. Indeed, the addition of further assumptions (which may be claimed to be implied by the original standard formulation) results in the generation of an improved formulation. From the abovementioned discussions there were only two problems remaining, namely 1) the proposed additional clarifying assumptions were divergent, and 2) the attempts at clarification led to the subject of QT which in itself does not have a generally agreed-upon solution (i.e., the QT measurement problem). Nevertheless, the author believes that these obstacles should not prevent attempts to improve the interpretation of the double-slit experiment by the explicit addition of the current implied assumptions.
In Section 2, a very brief description of the double-slit experiment is presented. Section 3 contains the standard explanation for when in QT interference occurs and when it does not occur. Section 4 lists the problems, questions and possible answers associated with the standard formulation. Sections 5 to 7 contain a proposal for an adaptation of the standard formulation to a “functional interpretation”. A functional interpretation (or functional description) specifies the dynamic evolution of the system in terms of state transitions and explicit actions and events.
2. The Double-Slit Experiment
Under the assumption that the reader is already familiar with the double-slit experiment, only a very short description is given:
The double-slit experiment demonstrates one of the most important features of QT, the relationship between the wave-like and the particle-like characteristics. In technical terms, the experiment shows the superposition of wave functions. To also show the destruction of the superposition, two variants of the double-slit experiment are typically discussed: 1) an experiment with photon source near the slits, and 2) an experiment without the photon source. Figure 1 contains the photon sources, but is used as a reference for both cases.
2.1. Double-Slit Experiment without the Photon Sources near the Slits
The electron starts at the source with a spatial distribution such that the wave function propagates the electron through both slits.
The two paths partly reunite again behind the splits, producing the interference pattern at the electron detector.
2.2. Double-Slit Experiment with the Photon Sources near the Slits
In addition to the process description given above, the electron wave passing the photon source may interact with a photon emitted by the photon source in such a way that the electrons wave function “collapses” and interference ceases.
Figure 1. Double-slit experiment.
3. The Standard Explanation
In textbooks of QT, the double-slit experiment is often used to explain one of the key principles of QT which in this paper is called the “interference rule”. Here, we refer to the formulation of R. Feynman. The interference rule,in the context of explaining the double-slit experiment,is explained by Feynman in [2] as follows:
“When an event can occur in several alternative ways, the probability amplitude for the event is the sum of the probability amplitudes for each way considered separately”. There is interference:

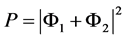
If an experiment is performed which is capable of determining whether one or another alternative is taken, the probability of the event is the sum of the probabilities for each alternative. The interference is lost.
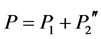
This interference (collapse) rule or slight variations of it, is contained in all textbooks on basic QT, either as an explanation of the double slit experiment. Or vice versa the double slit experiment is used to illustrate the rule. Without the photon sources near the slits, interference occurs. The inclusion of the photon source aborts the interference.
4. Attempting to Understand the “Interference Rule”
Currently, when one attempts to map the interference rule to a computer program that has the objective of simulating the double-slit experiment it turns out that this simulation is not possible. The problem is that a condition such as that of an experiment capable of determining whether one or another alternative is taken can neither reasonably be mapped to any mathematical constructs, nor to a physical facts-driven decision algorithm because it does not refer to elements of a physical state, but to some “capability of determining”. With a closer examination of the situation, it becomes clear that this is not a problem of writing a specific computer program; rather, the lack of comprehension is more general in nature.
The lack of comprehension can be expressed in the following list of question that can be asked with respect to the interference collapse rule:
1) Why is it said “capable of determining” as opposed to “is determined”?
2) What are the precise rules that allow me (or a computer program) to decide whether my experiment is capable of determining?
3) Does the condition “capable of determining” always refer to an observation or event (e.g. measurement) during the movement of the waves during the waves towards the observation of the interference pattern? Or are other capabilities of determining imaginable?
4) In QT it is often the case that the capability to decide between A and B is a matter of probability. Does the interference rule apply also to probabilistic decisions? Or does the rule assume decisions with certainty?
5) Does the rule state a logical implication (i.e., IF a THEN b) or a logical identity (i.e., IF a THEN b AND IF b THEN a)? In other words, if interference ceases, does this also imply that it should be in principle possible to determine which alternative was taken?
5. A Functional Interpretation of the Double-Slit Experiment
Attempts to defend and explain the standard QT interference rule typically focus on an answer to question 3 above (“Does the condition ‘capable of determining’ always refer to an observation or event (e.g. measurement)... ?”). Therefore let us attempt a modification of the standard QT interference rule which clarifies which types of events may occur that are capable of causing a collapse of the interference in regard to the electron wave on its way to the screen.
The proposed modification is the following:
“Interference is lost (i.e., the probabilities must be added) if through a measurement it is possible to determine that a particular path is taken”.
This phrasing still requires that the term “measurement” be more precisely defined. However, when a situation may be considered to exactly represent a measurement is one of the open questions of the unresolved measurement problem. At minimum, it is controversial whether the addition of the photon source in the double-slit experiment represents a measurement.
6. A Functional Interpretation of the QT Measurement Process
In [3] an explanation of the QT measurement and of the QT measurement problem is given that may also serve as a basis for an improved interference collapse rule. The concept described in [3] may be summarized as follows:
1. A measurement always implies interactions between the measured quantum object and the measurement environment. Measurements of QT observables can be performed using a variety of measurement devices, apparatuses, and processes. All such measurement processes must include at least one interaction in which the measured object exchanges information with some other entity belonging to the measurement apparatus.
2. The model of measurement is based on “QFT interactions”. QFT interactions are “normal” interactions between the measured QT object and the measurement apparatus that adhere to the laws of quantum field theory (QFT) and must be treated using methods of QFT.
3. In general, the interacting particles/waves consist of multiple “paths” with different associated probability amplitudes. The interaction always occurs at a definite position. Only the paths that cover the interaction position determine the result of the (measurement) interaction.
4. The measurement process includes a collapse of the wave function. After the interacting paths are determined and used to generate the interaction result (i.e., measurement result), all of the remaining paths are discarded. This process may be considered to be the “collapse of the wave function”.
5. Interactions support only a non-bijective mapping of the “in” state to the “out” state and thus only the limited exchange of information. This limited exchange of information is the cause of some of the limitations and peculiarities of QT measurements.1
7. A Functional Formulation of the Interference Collapse Rule
With the above described functional interpretation of the QT measurement process, it is possible to unify the collapse of the interference (as it may, for example, occur in the double-slit experiment) with the collapse of the wave function associated with QT measurement and to reformulate the interference collapse rule as follows:
Interference is lost (i.e., the probabilities must be added) if the particle/wave becomes involved in a QFT interaction on its way to the observation target.
8. Discussion
8.1. Alternative Collapse or No-Collapse Theories
The above proposed improved interference collapse rule is based on a functional model of QT measurement as described in [3] . This functional model of QT measurement contains as a major ingredient the assumption of the collapse of the wave function. The collapse of the wave function, however, is not generally agreed upon among physicists. Many physicists believe in the many worlds theory (see [5] ) which denies a collapse of the wave function and instead assumes branching into (many) new worlds. Because the many worlds theory replaces the discontinuity (i.e., the collapse) of the wave function progression by another type of discontinuity (the branching into many worlds), the proposed interference collapse rule is also compatible with the many worlds theory.
The same holds true for alternative collapse theories, such as, for example, the GRW theory (see [6] and [7] ). (The GRW theory achieves the collapse of the wave function through a modification of the (linear) Schrödinger equation, such that it becomes non-linear). The specific collapse mechanism (or no-collapse theory) does not necessarily prevent prevent the generation of unique models for the collapse of the wave function and the interference collapse rule. Rather, it can be said, that a specific collapse (or no-collapse) theory is the more plausible, if it is not restricted to the QT measurements, but also applies to general QT interferences.
8.2. What Is a QFT Interaction?
The proposed interference collapse rule associates the collapse of the interference (as well as the collapse of the wave function) with the occurrence of a “QFT interaction”. In [4] a QFT-interaction is defined as an interaction whose results must be computed with the techniques of quantum field theory (e.g. scattering matrix, Feynman diagrams and Feynman rules). There are other types of interactions (mostly appearing in classical QT (gedanken-) experiments) which can be handled without QFT. A more precise and formal differentiation between QFT-interactions and non-QFT-interactions would be desirable, but can currently not be provided (at least not by the author).
9. Conclusions
The traditional interference collapse rule in quantum theory appears to be simple, albeit mysterious. Upon closer examination, as necessitated by the attempt to map the rule to a computer program, it turns out that the traditional interference collapse rule does not provide satisfactory answers to a number of questions regarding its precise meaning.
An alternative to, or at least modification of the traditional interference collapse rule is proposed by the author unifying of the collapse of interference as it occurs in the double-slit experiment and the collapse of the wave function associated with QT measurements. Unfortunately this alternative leads to the QT measurement problem for which there exists apparently no generally agreed upon theory. Nevertheless, the proposed “interference collapse rule” is considered by the author to be an improvement, because (a) it refers to criteria that have well-defined meanings within QT, and (b) it is compatible with a variety of interpretations of QT measurement, including the authors functional model of the QT measurement process described in [3] and the many-worlds theory described in [5] .
Cite this paper
Hans H. Diel, (2015) An Improved “Interference Collapse Rule” of Quantum Mechanics. Open Access Library Journal,02,1-5. doi: 10.4236/oalib.1101838
References
- 1. Diel, H.H. (2013) A Computer Model of Quantum Field Theory. Proceedings of World Academy of Science, Engineering and Technology, Vol. 80, 77-84.
- 2. Feynman, R.P., Leighton, R.B. and Sands, M. (1971) The Feynman Lectures on Physics, Volume 3: Quantum Mechanics. Addison-Wesley, London.
- 3. Diel, H.H. (2014) A Model of the Measurement Process in Quantum Theory.
http://arxiv.org/abs/1405.5982v1 - 4. Diel, H.H. (2015) A Functional Model of Interactions in Quantum Theory.
http://arxiv.org/abs/1405.6099v2 - 5. Everett III, H. (1957) “Relative State” Formulation of Quantum Mechanics. Reviews of Modern Physics, 29, 454.
http://dx.doi.org/10.1103/RevModPhys.29.454 - 6. Girardi, G.C., Rimini, A. and Weber, T. (1985) A Model for a Unified Quantum Description of Macroscopic and Microscopic Systems. In: Accardi, L. and von Waldenfels, W., Eds., Quantum Probability and Applications II, Springer, Berlin, 223-232.
http://dx.doi.org/10.1007/BFb0074474 - 7. Diosi, L. (2015) Is Spontaneous Wave Function Collapse Testable at All? Journal of Physics: Conference Series, 626, Article ID: 012008.
http://dx.doi.org/10.1088/1742-6596/626/1/012008
NOTES
1This point is explained in more detail in [4] . For the present paper this point is not important.



