Open Access Library Journal
Vol.02 No.08(2015), Article ID:68575,6 pages
10.4236/oalib.1101805
Can Von Neumann’s Theory Meet Quantum Computation?
Koji Nagata1, Tadao Nakamura2
1Department of Physics, Korea Advanced Institute of Science and Technology, Daejeon, Korea
2Department of Information and Computer Science, Keio University, Yokohama, Japan
Email: ko_mi_na@yahoo.co.jp, nakamura@pipelining.jp
Copyright © 2015 by authors and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 28 July 2015; accepted 21 August 2015; published 24 August 2015

ABSTRACT
Recently, it is shown that there is a crucial contradiction within von Neumann’s theory [K. Nagata and T. Nakamura, Int. J. Theor. Phys. 49, 162 (2010)]. We derive a proposition concerning a quantum expected value under the assumption of the existence of the directions in a spin-1/2 system. The quantum predictions within the formalism of von Neumann’s projective measurement cannot coexist with the proposition concerning the existence of the directions. Therefore, we have to give up either the existence of the directions or the formalism of von Neumann’s projective measurement. Hence, there is a crucial contradiction within von Neumann’s theory. We discuss that this crucial contradiction makes the theoretical formulation of Deutsch’s algorithm questionable. Especially, we systematically describe our assertion based on more mathematical analysis using raw data. Our discussion, here, improves previously published argumentations very much.
Keywords:
Quantum Measurement Theory, Quantum Computer, Formalism
Subject Areas: Applied Physics

1. Introduction
Von Neumann introduces the Hilbert space and he tries to present axioms of quantum mechanics [1] . He introduces projective measurement theory. For example, the values of the result of quantum measurements are  (in
(in 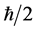 unit) in spin-1/2 system. An important note here, von Neumann’s theory does not say that we can measure non-commuting observables, simultaneously. Therefore, each value of measurement depends time even though we do not indicate any suffix concerning time. The detail argument can be seen in Ref. [2] where we indicate a suffix concerning time. von Neumann’s theory is necessary to perform quantum computer. It is said that there is not any quantum computer without von Neumann’s theory.
unit) in spin-1/2 system. An important note here, von Neumann’s theory does not say that we can measure non-commuting observables, simultaneously. Therefore, each value of measurement depends time even though we do not indicate any suffix concerning time. The detail argument can be seen in Ref. [2] where we indicate a suffix concerning time. von Neumann’s theory is necessary to perform quantum computer. It is said that there is not any quantum computer without von Neumann’s theory.
A quantum computer is a device for computation that makes direct use of quantum mechanical phenomena, such as superposition and entanglement, to perform operations on data. Quantum computers are different from digital computers based on transistors. Whereas digital computers require data to be encoded into binary digits (bits), quantum computation utilizes quantum properties to represent data and perform operations on these data [3] . A theoretical model is the quantum Turing machine, also known as the universal quantum computer. Quantum computers share theoretical similarities with non-deterministic and probabilistic computers, like the ability to be in more than one state simultaneously. The field of quantum computing was first introduced by Richard Feynman in 1982 [4] [5] .
Here we review to discuss that there is a crucial contradiction within von Neumann’s formalism of the quantum theory [2] [6] [7] . Especially, we reexamine the quantum-theoretical formulation of Deutsch’s algorithm [8] as the earliest quantum computer. We result in the fact that the formulation is questionable despite the fact that we indeed have raw experimental data. We systematically describe our assertion based on more mathe- matical analysis using raw data. This point gives us new important insight rather than the argumentations presented in Refs. [2] [6] [7] .
We review the contradiction as follows. We derive a proposition concerning a quantum expected value under the assumption of the existence of the directions in a spin-1/2 system. The quantum predictions within the formalism of von Neumann’s projective measurement (the results of measurements are ) cannot coexist with the proposition concerning the existence of the directions. Therefore, there is a crucial contradiction in the set of propositions of von Neumann’s theory in a spin-1/2 system.
) cannot coexist with the proposition concerning the existence of the directions. Therefore, there is a crucial contradiction in the set of propositions of von Neumann’s theory in a spin-1/2 system.
2. There Is a Contradiction within Von Neumann’s Theory
First, we review that there is a contradiction within von Neumann’s theory along with the argumentation of Ref. [7] .
Assume a pure spin-1/2 state 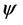 lying in the x-y plane. Let
lying in the x-y plane. Let 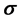 be
be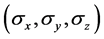 , the vector of Pauli ope- rators. The measurements (observables) on a spin-1/2 state lying in the x-y plane of
, the vector of Pauli ope- rators. The measurements (observables) on a spin-1/2 state lying in the x-y plane of 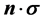 are parameterized by a unit vector
are parameterized by a unit vector  (its direction along which the spin component is measured). Here,
(its direction along which the spin component is measured). Here, 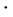 is the scalar product in
is the scalar product in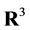 .
.
We have a quantum expected value  as
as
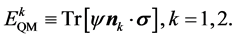 (1)
(1)
We have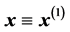 ,
,  , and
, and  which are the Cartesian axes relative to which spherical angles are measured. Let us write the two unit vectors in the plane defined by
which are the Cartesian axes relative to which spherical angles are measured. Let us write the two unit vectors in the plane defined by 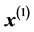 and
and 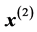 in the following way:
in the following way:

Here, the angle 

We derive a necessary condition for the quantum expected value for the system in a pure spin-1/2 state lying
in the x-y plane given in (1). We derive the possible values of the product

the quantum expected value given in (1). We see that
introduce simplified notations as 


where we use the orthogonality relation
sphere (the directions) with the value of 

the Bloch sphere 
value under the assumption of the existence of the directions (in a spin-1/2 system), that is,


when the system is in a pure state lying in the x-y plane


On the other hand, let us assume von Neumann’s projective measurement. In this case, the quantum mean value, which is the average of the results of projective measurements, is given by

We can assume as follows by Strong Law of Large Numbers,

where 




where






And

By using these facts, we derive a necessary condition for the quantum mean value for the system in a pure spin-1/2 state lying in the x-y plane given in (5). The quantum mean value 

Clearly, the above inequality can be saturated since, as we have said,

and

We derive the possible values of the product
proposition concerning a quantum mean value under the assumption that von Neumann’s projective mea-
surement is true (in a spin-1/2 system), that is,

of Large Numbers, we have

Thus, we have

Hence we derive the following proposition concerning von Neumann’s projective measurement

Clearly, we cannot assign the truth value “1” for two propositions (4) (concerning the existence of the directions) and (15) (concerning von Neumann’s projective measurement), simultaneously, when the system is in a pure state lying in the x-y plane. Therefore, we are in the contradiction when the system is in a pure state lying in the x-y plane.
3. Deutsch’s Algorithm
Next, we review Deutsch’s algorithm along with Ref. [9] .
Quantum parallelism is a fundamental feature of many quantum algorithms. It allows quantum computers to evaluate the values of a function 




modulo 2. We give the transformation defined by the map 

Deutsch’s algorithm combines quantum parallelism with a property of quantum mechanics known as interference. Let us use the Hadamard gate to prepare the first qubit 


state

see what happens in this circuit. The input state

is sent through two Hadamard gates to give

A little thought shows that if we apply 





The final Hadamard gate on the first qubit thus gives us

Realizing that 


So by measuring the first qubit we may determine



4. A Problem of Deutsch’s Algorithm
In what follows, we discuss a problem of Deutsch’s algorithm. We see that the implementation of Deutsch’s algorithm is not possible if we give up either observability of a quantum state or controllability of a quantum state.
We introduce the following quantum proposition concerning controllability:

We may consider the following non-quantum-theoretical proposition:

The proposition (22) implies the validity of von Neumann’s projective measurement (observability). The proposition (22) implies

However, the validity of von Neumann’s projective measurement does not imply the proposition (22). We see that the proposition (21) is not equivalent to von Neumann’s projective measurement (observability). We see that we can assign the truth value “1” for von Neumann’s projective measurement (observability) and we can assign the truth value “0” for the proposition (21) concerning controllability.
The proposition (21) implies that 
the x-y plane. The reason is as follows: Assume a pure state lying in the x-y plane as 



and

proposition (21) implies that there are directions in the Hilbert space formalism of the quantum theory.
From the discussion presented in the previous, we see that the quantum proposition (21) concerning con- trollability (the directions) cannot coexist with the validity of von Neumann’s projective measurement (obser-
vability), which states
Deutsch’s algorithm shows the importance of the ability of the Hadamard gate (controllability and the existence of the directions) for quantum computation. The ability of the Hadamard gate is valid only when we assign the truth value “1” for the proposition (21) (the directions). We see that the quantum state 

only when we assign the truth value “1” for the proposition (21) concerning controllability (directions) and we give up the validity of von Neumann’s projective measurement (observability). The validity of the proposition (21) implies that

We conclude that the step in which transforms the state 

5. Conclusions
In conclusion, we have reviewed that there is a crucial contradiction within von Neumann’s theory. We have reexamined the quantum-theoretical formulation of Deutsch’s algorithm as the earliest quantum computer. We have resulted in the fact that the formulation has been questionable despite the fact that we have indeed had raw experimental data. We have questioned what makes observability if we accept the ability of the Hadamard gate (controllability and the directions). We have questioned what makes controllability if we accept the validity of von Neumann’s projective measurement (observability). Especially, we have systematically described our asser- tion based on more mathematical analysis using raw data. This point improves previously published argumen- tations very much.
What are new physical theories? We cannot answer it at this stage. However, we expect that our discussion in this thesis could contribute to creating new physical theories in order to explain the handing of raw experimental data, to create new information science, and to predict new unknown physical phenomena efficiently.
Cite this paper
Koji Nagata,Tadao Nakamura, (2015) Can Von Neumann’s Theory Meet Quantum Computation?. Open Access Library Journal,02,1-6. doi: 10.4236/oalib.1101805
References
- 1. von Neumann, J. (1955) Mathematical Foundations of Quantum Mechanics. Princeton University Press, Princeton.
- 2. Nagata, K., Ren, C.-L. and Nakamura, T. (2011) Whether Quantum Computation Can Be Almighty. Advanced Studies in Theoretical Physics, 5, 1.
- 3. Gershenfeld, N. and Chuang, I.L. (1998) Quantum Computing with Molecules.
- 4. Deutsch, D. (1992) Quantum Computation. Physics World.
- 5. Quantum Computer—Wikipedia, the Free Encyclopedia.
- 6. Nagata, K. and Nakamura, T. (2010) Can von Neumann’s Theory Meet the Deutsch-Jozsa Algorithm? International Journal of Theoretical Physics, 49, 162-170.
http://dx.doi.org/10.1007/s10773-009-0189-5 - 7. Nagata, K. (2009) There Is No Axiomatic System for the Quantum Theory. International Journal of Theoretical Physics, 48, 3532-3536.
http://dx.doi.org/10.1007/s10773-009-0158-z - 8. Deutsch, D. (1985) Quantum Theory, the Church-Turing Principle and the Universal Quantum Computer. Proceedings of the Royal Society of London A, 400, 97.
http://dx.doi.org/10.1098/rspa.1985.0070 - 9. Nielsen, M.A. and Chuang, I.L. (2000) Quantum Computation and Quantum Information. Cambridge University Press, Cambridge.


