Open Access Library Journal
Vol.02 No.08(2015), Article ID:68573,4 pages
10.4236/oalib.1101803
Do the Two Operations Addition and Multiplication Commute with Each Other?
Koji Nagata1, Tadao Nakamura2
1Department of Physics, Korea Advanced Institute of Science and Technology, Daejeon, Korea
2Department of Information and Computer Science, Keio University, Yokohama, Japan
Email: ko_mi_na@yahoo.co.jp, nakamura@pipelining.jp
Copyright © 2015 by authors and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 30 July 2015; accepted 21 August 2015; published 24 August 2015

ABSTRACT
We study about the metamathematics of Zermelo-Fraenkel set theory with the axiom of choice. We use the validity of Addition and Multiplication. We provide an example that the two operations Addition and Multiplication do not commute with each other. All analyses are performed in a finite set of natural numbers.
Keywords:
Set Theory, Formalism
Subject Areas: Applied Physics

1. Introduction
Zermelo-Fraenkel set theory with the axiom of choice, commonly abbreviated ZFC, is the standard form of axiomatic set theory and as such is the most common foundation of mathematics. It has a single primitive ontological notion, that of a hereditary well-founded set, and a single ontological assumption, namely that all individuals in the universe of discourse are such sets. ZFC is a one-sorted theory in first-order logic. The signature has equality and a single primitive binary relation, set membership, which is usually denoted Î. The formula 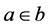 means that the set a is a member of the set b (which is also read, “a is an element of b” or “a is in b”). Most of the ZFC axioms state that particular sets exist. For example, the axiom of pairing says that given any two sets a and b there is a new set
means that the set a is a member of the set b (which is also read, “a is an element of b” or “a is in b”). Most of the ZFC axioms state that particular sets exist. For example, the axiom of pairing says that given any two sets a and b there is a new set 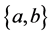 containing exactly a and b. Other axioms describe properties of set membership. A goal of the ZFC axioms is that each axiom should be true if interpreted as a statement about the collection of all sets in the von Neumann universe (also known as the cumulative hierarchy). The me- tamathematics of ZFC has been extensively studied. Landmark results in this area that is established the in- dependence of the continuum hypothesis from ZFC, and of the axiom of choice from the remaining ZFC axioms [1] . Mach literature concerning above topic can be seen in Refs. [2] - [18] .
containing exactly a and b. Other axioms describe properties of set membership. A goal of the ZFC axioms is that each axiom should be true if interpreted as a statement about the collection of all sets in the von Neumann universe (also known as the cumulative hierarchy). The me- tamathematics of ZFC has been extensively studied. Landmark results in this area that is established the in- dependence of the continuum hypothesis from ZFC, and of the axiom of choice from the remaining ZFC axioms [1] . Mach literature concerning above topic can be seen in Refs. [2] - [18] .
We use the validity of Addition and Multiplication. Here we aim to provide an example that the two opera- tions Addition and Multiplication do not commute with each other. All analyses are performed in a finite set of natural numbers.
2. The Two Operations Addition and Multiplication Do Not Commute with Each Other
Assume all axioms of Zermelo-Fraenkel set theory with the axiom of choice is true.
Let us start with a singleton set
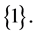 (1)
(1)
We treat here Addition. We have
 (2)
(2)
Thus we obtain 2. By using the obtained 2, we have
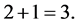 (3)
(3)
Thus we obtain 3. By repeating this method for an even number time, we have
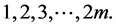 (4)
(4)
By repeating this method, we have
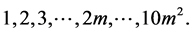 (5)
(5)
Thus we have the following finite set of natural numbers
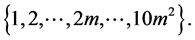 (6)
(6)
By using the set (6), we discuss that the two operations Addition and Multiplication do not commute with each other.
We consider a value V which is the sum of the results of trials. Result of trials is 1 or 2. We assume the number of 2 is equal to the number of 1. The number of trials is 2 m. We have
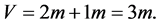 (7)
(7)
We derive the possible value of the product  of the value V. It is
of the value V. It is
 (8)
(8)
We assign the truth value “1” for the following proposition
 (9)
(9)
We have
 (10)
(10)
The value  which is the sum of the results of trials is given by
which is the sum of the results of trials is given by
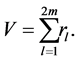 (11)
(11)
We assume that the possible value of the actually happened results 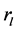 is 1 or 2. We have
is 1 or 2. We have
 (12)
(12)
The same value is given by

We only change the labels as 



and

Here







The step (16) to (17) is OK. The step (17) to (18) is valid under the assumption that the two operations Addition and Multiplication commute with each other. The step (18) to (19) is true since we have only changed the label as
The above inequality (19) is saturated since

and

We derive a proposition concerning the value given in (11) under the assumption that the possible value of the actually happened results is 1 or 2, that is

We do not assign the truth value “1” for the two propositions (10) and (24) simultaneously. We are in a contradiction. Thus we have to give up the assumption that the two operations Addition and Multiplication commute with each other.
3. Conclusion
In conclusions, we have used the validity of Addition and Multiplication. We have provided an example that the two operations Addition and Multiplication do not commute with each other. All analyses have been performed in a finite set of natural numbers.
Cite this paper
Koji Nagata,Tadao Nakamura, (2015) Do the Two Operations Addition and Multiplication Commute with Each Other?. Open Access Library Journal,02,1-4. doi: 10.4236/oalib.1101803
References
- 1. Zermelo-Fraenkel Set Theory—Wikipedia, the Free Encyclopedia.
- 2. Abian, A. (1965) The Theory of Sets and Transfinite Arithmetic. W B Saunders.
- 3. Abian, A. and LaMacchia, S. (1978) On the Consistency and Independence of Some Set-Theoretical Axioms. Notre Dame Journal of Formal Logic, 19, 155-158.
http://dx.doi.org/10.1305/ndjfl/1093888220 - 4. Devlin, K. (1984) The Joy of Sets. Springer.
- 5. Fraenkel, A., Bar-Hillel, Y. and Levy, A. (1958) Foundations of Set Theory. Fraenkel’s Final Word on ZF and ZFC, North Holland.
- 6. Hatcher, W. (1968) The Logical Foundations of Mathematics. Pergamon.
- 7. Jech, T. (2003) Set Theory: The Third Millennium Edition, Revised and Expanded. Springer.
- 8. Kunen, K. (1980) Set Theory: An Introduction to Independence Proofs. Elsevier.
- 9. Montague, R. (1961) “Semantic Closure and Non-Finite Axiomatizability” in Infinistic Methods. Pergamon, London, 45-69.
- 10. Suppes, P. (1960) Axiomatic Set Theory. Dover Reprint. Perhaps the Best Exposition of ZFC before the Independence of AC and the Continuum Hypothesis, and the Emergence of Large Cardinals. Includes Many Theorems.
- 11. Takeuti, G. and Zaring, W.M. (1971) Introduction to Axiomatic Set Theory. Springer Verlag.
- 12. Tarski, A. (1939) On Well-Ordered Subsets of Any Set. Fundamenta Mathematicae, 32, 176-183.
- 13. Tiles, M. (1989) The Philosophy of Set Theory. Dover Reprint. Weak on Metatheory; the Author Is Not a Mathematician.
- 14. Tourlakis, G. (2003) Lectures in Logic and Set Theory. Vol. 2, Cambridge University Press, Cambridge.
- 15. van Heijenoort, J. (1967) From Frege to Godel: A Source Book in Mathematical Logic, 1879-1931. Harvard Univ. Press. Includes Annotated English Translations of the Classic Articles by Zermelo, Fraenkel, and Skolem Bearing on ZFC.
- 16. Zermelo, E. (1908) Untersuchungen uber die Grundlagen der Mengenlehre I. Mathematische Annalen, 65, 261-281.
http://dx.doi.org/10.1007/BF01449999 - 17. van Heijenoort, J. (1967) Investigations in the Foundations of Set Theory. From Frege to Godel: A Source Book in Mathematical Logic, 1879-1931. Source Books in the History of the Sciences, Harvard University Press, 199-215.
- 18. Zermelo, E. (1930) Uber Grenzzablen und Mengenbereiche. Fundamenta Mathematicae, 16, 29-47.


