Open Access Library Journal
Vol.02 No.08(2015), Article ID:68567,14 pages
10.4236/oalib.1101623
Applications of Clustering Algorithms in Academic Performance Evaluation
Jyotirmay Patel1, Ramjeet Singh Yadav2
1Department of Computer Science and Engineering, Meerut Institute of Technology, Meerut, India
2Department of Computer Science and Engineering, Ashoka Institute of Technology and Management, Varanasi, India
Email: jyotirmaypatel@gmail.com
Copyright © 2015 by authors and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 31 July 2015; accepted 18 August 2015; published 21 August 2015

ABSTRACT
In this paper, we explore the applicability of K-means and Fuzzy C-Means clustering algorithms to student allocation problem that allocates new students to homogenous groups of specified maximum capacity, and analyze effects of such allocations on the academic performance of students. The paper also presents a Fuzzy set and Regression analysis based Dynamic Fuzzy Expert System model which is capable of dealing with imprecision and missing data that is commonly inherited in the student academic performance evaluation. This model automatically converts crisp sets into fuzzy sets by using C-Means clustering algorithm method. The comparative performance analysis indicates that the student group formed by Fuzzy C-Means clustering algorithm performed better than groups formed by K-Means, classical fuzzy logic clustering algorithms and Bayesian classifications.
Keywords:
Student Allocation Problem, Academic Performance, Fuzzy C-Means, K-Means, Clustering Algorithms
Subject Areas: Computer Engineering

1. Introduction
Student academic performance evaluation involves several components, each based on number of imprecise judgments arising due to human (teacher/tutor) interpretation. Both arithmetical and statistical methods have been used for aggregating information from these assessment components in educational domain. These commonly used methods have some limitations. For example, in a scenario, two student’s scores are 50, 60, 70, and 70, 60, 50 in three tests, respectively. The average mark obtained by each is 60 without any indication of their intelligence level. However, data indicate that one student is improving while other is deteriorating consistently (i.e. one student is learning consistently). Recently, methods have been developed for the application of fuzzy set theory in student performance evaluation and concept maps construction which provides adaptive learning guidance to students. Learning achievement evaluation needs solution of subjective judging problem, difficulty and complexity of questions faced by the teachers [1] . Concept maps construction for adaptive learning guidance to students requires consideration of achievement similarity between concepts [2] .
The main aim of educational institutions is to provide student with the evaluation reports regarding their test/ examination as best as possible with minimum errors. Some factors other than academic have been reported to creates/pose barrier to students attaining and maintaining their high performance [3] . Grouping or clustering of students using cognitive as well as affective factors and then defining the performance measure may be a realistic approach. Fuzzy evaluation method (FEM) for applying fuzzy sets in students’ answer script evaluation [4] may serve the purpose. The fuzzy marks awarded to student’s answer scripts can be represented by fuzzy sets. In a fuzzy set, the grade of membership of an element ui in the universe of discourse U belonging to a fuzzy set is represented by a real value between zero and one. The present study argued that the arithmetical and statistical techniques for classification and grading student academic performance have several limitations and are least appropriate to evaluate knowledge and skills. The present paper includes the role of fuzzy logic, fuzzy system, various characteristics of fuzzy logic system, linguistic variables, rules and membership functions and the implementation of performance analysis methodology with the help of fuzzy logic system. Reasoning based on fuzzy models and fuzzy clustering methods may yield alternative methods having potential to handle various kinds of imprecise data and improve the degree of judgments.
Some works related to academic performance evaluation based on Fuzzy sets and other soft computing techniques have been developed. Methods based on fuzzy sets and fuzzy rule base to assign grades to students and calculate the students’ academic performance are available [5] [6] . Non-classical performance evaluation methods (such as fuzzy logic, a mathematical technique of set-theory) can also be applied to many forms of decision-making including research on engineering and artificial intelligence [7] . A fuzzy system, a mathematical model, that analyzes input values in terms of logical values in addition to numerical values. In fuzzy logic applications non-numeric linguistic variables are often used to facilitate the expression of rules and facts. The performance appraisal system can be examined using Fuzzy Logic Approach [8] as in the present study. Cascaded fuzzy inference system based on specific performance appraisal has been used to generate the performance qualities of some non-teaching staff of Universities [9] [10] . A novel fuzzy qualitative classification system for academic performance evaluation using the link analysis methodology has been developed. Unlike the conventional approach, fuzzy rules based model involve variables, classes and their relations as elements of social network that can be modeled as a weighted graph [11] . Hameed has presented a more reliable system of student evaluation based on Gaussian membership functions [12] where three fuzzy nodes system (each nodes applies fuzzification, fuzzy inference, and defuzzification) has been considered (i.e. difficulty, importance and complexity of questions). Expert system technology using Fuzzy Logic is very interesting for qualitative facts evaluation; model of fuzzy expert system based on various key performance attributes is available to evaluate teacher’s performance [13] . Also the fuzzy method has been applied in evaluation of student’s oral presentation which involves application of membership function graph to identify the membership value of each satisfaction level [14] [15] . Fuzzy logic based engineering student’s evaluation for practical is studied in [16] [17] . Such student’s performance in three sub-components showed difference in outcome compared to classical approach. The fuzzy based approach to circumvent the performance evaluation of the student based purely upon the numeric grading without entailing the human judgmental component [18] . Evaluations of Government officer’s performance with the help of various parameters have been carried out by applying fuzzy inference system (FIS) [19] . This help in formulation of mapping from a given input. The fuzzy logic systems enable one to validly predict distance student’s performance according to the expert opinion [20] [21] . FIS for student academic performance evaluation is based on Fuzzy Logic Techniques where performance depends on exam results and it is evaluated as success or failure [22] . Methods to measure the performance of the students in junior high school [23] , performance of teachers [24] , and determination of grades to the students [25] are available. System considering the difficulty, the importance and the complexity of each question before determining a final grade [26] has also been worked out. Considerable attention has been given to adopt fuzzy approaches for evaluation of teaching performance by using computer particularly in Intelligent Tutoring Systems (ITS) and Computer Assisted Instruction (CAI) [27] [28] . Fuzzy approaches have been proposed for determination of student’s understanding level of certain subjects in context of ITS, and student performance based on several criteria with a strong suggestion that the method be applied to CAI. Currently, much attention has been given to such aspects globally. This includes evaluation of journal grades, evaluation of vocational education performance, collaborative assessment, and performance appraisal system of academic in higher education. Data Mining (DM) or Knowledge Discovery in Databases (KDD) is an approach for shorting useful information from large data [29] . DM applies various methods in order to discover and extract patterns from stored data, and is widely used in educational field to find out hidden patterns. Educational data mining is focus of research for studying the behavior of students based upon their past performance [30] - [33] .
2. Fuzzy Logic
Fuzzy logic is branch of logic specially designed for representing knowledge and human reasoning in such a way that it is amenable to processing by a computer. Thus, it is applicable to artificial intelligence, control engineering, and expert systems. The more traditional propositional and predicate logic do not allow for degrees of imprecision, indicated by words of phrases such as poor, average and good. Instead of truth values such as true or false, it is possible to introduce a multivalued logic consisting of Unsatisfactory, Satisfactory, Average, Good, and Excellent. Fuzzy systems implement fuzzy logic, which uses sets and predicates of this kind. As the classic logic is the basic of ordinary expert logic, fuzzy logic is also the basic of fuzzy expert system. Fuzzy expert systems, in addition to dealing with uncertainty, are able to model common sense reasoning which is very difficult for general systems. One of the basic limitations of classic logic is that it is restricted to two values, true or false and its advantage is that it is easy to model the two-value logic systems and also we can have a precise deduction. The major shortcoming of this logic is that, the number of the two-value subjects in the real world is few. The real world is an analogical world not a numerical one. We can consider fuzzy logic as an extension of a multi-value logic, but the goals and application of fuzzy logic is different from multi-value logic since fuzzy logic is a relative reasoning logic not a precise multi-value logic. In general, approximation or fuzzy reasoning is the deduction of a possible and imprecise conclusion out of a possible and imprecise initial set.
Fuzzy Set
A fuzzy set A in a universe of discourse X is defined as the following set pairs
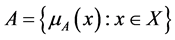 (1)
(1)
where, 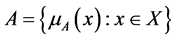 is a mapping called the membership function of fuzzy set A and
is a mapping called the membership function of fuzzy set A and 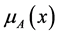 is called the degree of belongingness or membership value or degree of membership of
is called the degree of belongingness or membership value or degree of membership of 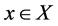 in the fuzzy set A. We write (1) in the following form:
in the fuzzy set A. We write (1) in the following form:
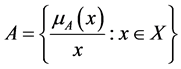 (2)
(2)
For brevity; however, we often equate fuzzy sets with their membership functions, i.e., we will often say fuzzy sets.
Example: Suppose X = {6, 2, 0, 4}. A fuzzy set of X may be given by A = {0.2/6, 1/2, 0.8/0, 0.1/4}.
3. K-Means Clustering Technique
The K-means clustering technique is an iterative algorithm in which items are moved among sets of clusters until the desired set is related. A high degree of similarity among elements in clusters is obtained, while a high degree of dissimilarity among elements in different clusters is achieved simultaneously. The K-Means clustering technique is used to classify data in a crisp sense. Define a family of sets 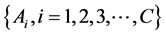 as a partition of X, where the following set-theoretic forms apply to those partitions:
as a partition of X, where the following set-theoretic forms apply to those partitions:
 (1)
(1)
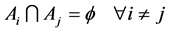 (2)
(2)
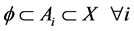 (3)
(3)
Again, where 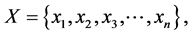 a finite set space is comprised of the universe of data samples, and C is the number of cases, or partitions, or clusters, into which we want to classify the data. We note the obvious,
a finite set space is comprised of the universe of data samples, and C is the number of cases, or partitions, or clusters, into which we want to classify the data. We note the obvious,
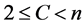 (4)
(4)
where C = n classes just places each data sample into its own class.
Here the objective function (or classification criteria) to be used to classify or cluster the data. The objective function 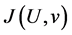 is given by:
is given by:
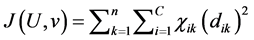 (5)
(5)
where U is the partition matrix, v is a vector of cluster centers and 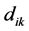 is a Euclidean distance measure between the kth data sample
is a Euclidean distance measure between the kth data sample 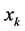 and ith cluster centre
and ith cluster centre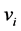 , is given by
, is given by
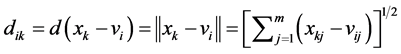 (6)
(6)
The algorithm is given below:
Step-I: Start with some initial configuration of prototypes 
Step-II: We compute the value for 


Step-III: Construct a partition matrix by assigning numeric values to U according to the following rule:

Step-IV: Update the prototype by computing the weighted average, which involves the entries of the partition matrix:

Until convergence criteria is met.
4. Fuzzy C-Means (FCM) Clustering Technique
The fuzzy C-Means algorithm (FCM) generalizes the classical fuzzy logic algorithm to allow a point to partially belong to multiple clusters. It produces a constrained soft partition. The extended objective function, denoted J, is

where U is a fuzzy partition of the dataset X formed by
to search for membership functions 




Bases on these formulae, FCM updates the prototypes and the membership function iteratively using Equations (10) and (11) until a convergence criterion is reached. The algorithm is given below:
FCM (X, c, m,
X: An unlabeled data set.
C: the number of clusters to form.
m: the parameter in the objective function.

Initialize prototype
Repeat
Compute membership function using Equation (10).
Update the prototype, vi in V using Equation (11).
Until
Until convergence criteria is met.
5. Bayesian Classification
Bayesian Classifiers are statistical classifiers. They can predict class membership probabilities, such as the probability that a given tuple belongs to a particular class. Bayesian classifiers assume that the effect of an attribute value on a given class is independent of the values of the other attributes. This assumption is called class conditional independence. Bayesian classification is based on Bayes’ theorem, described below: Let X be a data tuple. In Bayesian terms, X is considered evidence. It is described by measurements made on a set of n attributes. Let H be some hypothesis, such as that the data tuple X belongs to a specified class C. For classification problems, we want to determine



The Bayesian classifier works as follows:
1) Let D be a training set of tuples and their class labels. Each tuple is represented by n-dimensional attributes vector, 
2) Suppose that there are m classes, 






3) As 



4) Given data sets with many attributed, it would be extremely computationally expensive to compute 


5) In order to predict the class label of X, 






6. Fuzzy Logic, K-Means, Fuzzy C-Means and Bayesian Methods
This section includes implementation and testing of the student’s academic performance evaluation to achieve the objective(s) of research work proposed by using classical Fuzzy Logic based expert system, Bayesian, K- Means and Fuzzy C-Means and hybrid clustering (Subtractive Clustering, Subtractive Clustering-Fuzzy C-Means and Subtractive Clustering-Adaptive Neuro Fuzzy Inference System) methods. The proposed methods for student academic performance evaluation have been implemented in MATLAB. The marks, their associated original grade and level of achievement (i.e. very high, high, average, low and very low) are shown in Table 1. The dataset used for training and testing is a data set of 2050 student’s marks for Semester-1, Semester-2 and Semester-3 (Table 2 and Table 3). Out of total data sets, 2000 data sets have been used for training purpose and rest 50 used for testing purpose. These data sets have been collected from affiliated colleges of Uttar Pradesh Technical University, UP, Lucknow, India. We are considering grade and level of achievement as our own convention.
The proposed model was tested with the 17 new student’s marks for testing purpose (Table 4).
Table 1. Students marks, associated original grade and level of achievement.
Table 2. Student’s training data set.
Table 3. Student testing data set.
Table 4. Semester scores of 17 new students.
7. Fuzzy Logic Based Fuzzy Expert System
The rule based Fuzzy Expert System (FES) model (fuzzy-1 and fuzzy-2) for academic performance evaluation has been proposed. This model is based on classical fuzzy logic. The inputs (three) showed same triangular membership functions which indicate replacement of Semester-1 with Semester-3 would not change performance value (0.35, 0.45, and 0.75) and (0.75, 0.45, and 0.35) in Fuzzy-1 (see Table 5 of 16th and 17th students). If, symmetry or value range of the membership functions is dissimilar, one semester shows greater influence on performance value than the other. For example, let’s change the membership functions and value range of Semester-3, while retaining the original criteria for Semester-1 and Sem-2 examination (Fuzzy-2). Aim of this study arrangement in Sem-3 examination is penalize scores below 0.50 and to reward scores above 0.50. Comparisons of classical, fuzzy-1 and fuzzy-2 methods for student academic performance evaluation are given in Table 5. A student successful in the classical assessment method will also be successful in the fuzzy-1. Comparison of the classical method with fuzzy-2 revealed differences in the performance values. In case of scores <0.50, the performance value of fuzzy-2 is smaller than that of classical method; however, for scores >0.50, the performance value is greater than that of classical method (e.g. 7th student scoring 0.45 in sem-1, 0.433 in sem-2 and 0.54 in Sem-3 and unsuccessful in the classical and Fuzzy-1 methods, got success in the fuzzy-2). There is no change for scores of 0.50, because this is the boundary of the limit values (e.g. 8th student). The linear relationship among classical, fuzzy-1 and fuzzy-2 can be seen in the Figure 1.
The accuracy of proposed model for both training and testing data has been tested by the Root Mean Square Error (RMSE) (Table 6). Noticeable are the RMSE of fuzzy-2 model (0.1217) and RMSE of fuzzy-1 model (0.1312) for training data sets demonstrating benefits of fuzzy-2, obviously. In case of testing data, the lower RMSE for fuzzy-2 model compared to fuzzy-1 model further demonstrates the benefits of fuzzy-2.
Figure 1. Comparison of classical method, Fuzzy-1 and Fuzzy-2.
Table 5. Comparison of performance evaluation methods.
*Improved value.
Table 6. RMSE of training and testing data sets.
8. K-Means and FCM Methods
The data sets are divided into various clusters using K-Means and FCM methods with the help of MATLAB software. The students have been classified in five groups (Clusters): very high, high, average, low and very low. K-means and FCM methods work on finding the cluster centers by trying to minimize objective function. An error measure is then calculated for model validation. The root mean square error (RMSE) is used for this purpose. Comparison of Statistical, Fuzzy-2, K-Means and FCM method are shown in Table 7.
Noticeable is the 16th student, getting 0.35 marks in sem-1, 0.45 marks in sem-2 and 0.75 marks in sem-3 and assigned performance index as 0.52 in statistical method (Table 9). Similarly 17th student getting 0.75 marks in sem-1, 0.45 marks in sem-2 and 0.55 marks in sem-3 assigned performance index 0.52. These two students assigned performance index (0.54 and 0.45 in fuzzy-2 method; 0.68 and 0.42 in FCM method, respectively). It may be concluded that 16th student has improved consistently, while 17th student has deteriorated consistently. Therefore, the fuzzy C-Means clustering technique method is more suitable than the statistical, classical fuzzy and K-Means methods for academic performance evaluation. In this model, the numbers of fuzzy rules are very less in comparison to existing classical Fuzzy Expert System. Root Mean Square Error (RMSE) is employed to evaluate the accuracy of the model identification. The RMSE of FCM is 0.1012, RMSE of K-Means model goes to 0.1191, RMSE of fuzzy-2 model goes to 0.1217 and RMSE of fuzzy-1 model goes to 0.1312 for training data sets (Table 8), which demonstrates the benefits of FCM model obviously. RMSE of FCM is 0.1073, RMSE of K-Means model goes to 0.1099, RMSE of fuzzy-2 model goes to 0.1182 and RMSE of fuzzy-1 model goes to 0.1401 for testing data sets, which demonstrates the benefits of FCM model obviously.
The performances of objective function (K-Means and FCM Methods) for students’ academic performance evaluation are shown in Figure 2 and Figure 3. The objective function evolutions suggest that FCM method is better than K-means method.
Table 7. Comparison of Statistical, Fuzzy-2, K-Means and FCM Method.
*Improved value.
Figure 2. Objective function values of the K-Means method.
Figure 3. Performance of objective function of FCM Method.
Table 8. RMSE of training and testing data set.
9. Bayesian Approach
The predicted class label of students using Bayesian classification with the help of training data is given in Table 9. There are 14 data sets belonging to the class first, 14 data sets belonging to class second, 14 data sets belonging to class third and 8 data sets belonging to class fail. The training data sets are described by attributes like end semester marks, class test grade, seminar performance, assignment, general proficiency, attendance, and lab work. The class label attributes and class types have four distinct values namely first, second, third and fail. The allocation of any new student is shown in Table 10.
Table 9. Class-labeled training tuples from the student’s data set.
Table 10. Data set for a new student.
The need to maximize


puted based on the training data set. The Bayesian classifier more reliably predicts the new student belonging to class “first”. In the same manner any new student can be fitted to their respective class based on the performance. This research work focuses on the development of fuzzy logic and fuzzy C-means based fuzzy expert system to determine academic performance. Also presented is a new method for a new student allocation based on Bayesian approach. A difference in outcomes is seen between the classical and proposed fuzzy logic based expert systems methods when results are evaluated from fuzzy expert system. While the classical method adheres to a constant mathematical rule, evaluation with fuzzy logic has great flexibility and reliability. The proposed fuzzy C-Means based Fuzzy Expert System automatically converted the crisp data into fuzzy set and also calculates the total marks of a student who appeared in semsester-1, semester-2 and semester-3 examination. A simple and qualitative methodology to compare the predictive power of clustering algorithm and the Euclidean distance is evident as result of this work. The Fuzzy C-Means clustering models have improved on some limitation of the existing traditional methods, such as average method and statistical method. The Fuzzy C-Means algorithm is best model for modeling academic performance in an educational domain. However, due to multiple iterations and various Eigen vectors the FCM method suffers from heavy computational burdens and is time-consuming. Apart from this, it is also highly sensitive to the initialization which usually requires a priori knowledge of the cluster numbers to form the initial cluster centers. Such limitations can be mitigated by the Subtractive clustering based Tskagi-Sugeno (T-S) fuzzy model and combined Subtractive clustering with FCM called hybrid SC-FCM method.
10. Conclusion/Advantages and Disadvantages of the Proposed Algorithm
This research work focuses on the development of fuzzy logic based expert system and fuzzy C-means based fuzzy expert system to academic performance. We devised a new method to new student allocation based on Bayesian approach. A difference in outcomes is seen between the classical and proposed fuzzy logic based expert systems methods when results are evaluated from fuzzy expert system. While the classical method adheres to a constant mathematical rule, evaluation with fuzzy logic has great flexibility and reliability. The proposed FCM based Fuzzy Expert System automatically converted the crisp data into fuzzy set and also calculated the total marks of a student appeared in semsetr-1, semester-2 and semester-3 examination. A simple and qualitative methodology to compare the predictive power of clustering algorithm and the Euclidean distance is evident as result of this work. The FCM clustering models have improved on some limitation of the existing traditional methods, such as average method and statistical method. The FCM method is best model for modeling academic performance in educational domain compared the classical fuzzy logic. However, due to multiple iterations and various Eigen vectors, the FCM method suffers heavy computational burdens and is time-consuming.
Cite this paper
Jyotirmay Patel,Ramjeet Singh Yadav, (2015) Applications of Clustering Algorithms in Academic Performance Evaluation. Open Access Library Journal,02,1-14. doi: 10.4236/oalib.1101623
References
- 1. Bai, S.M. and Chen, S.M. (2006) Automatically Constructing Grade Membership Functions for Evaluating Students’ Evaluation for Fuzzy Grading. Proceeding of the 6th International Symposium on Soft Computing for Industry, Budapest, 24-26 July 2006, 1-6.
- 2. Bai, S.M. and Chen, S.M. (2008) Automatically Constructing Concept Maps Based on Fuzzy Rules for Adaptive Learning Systems. Expert System with Applications, 35, 41-49.
http://dx.doi.org/10.1016/j.eswa.2007.06.013 - 3. Sansgiry, S.S., Bhosle, M. and Sail, K.K. (2006) Factors That Affect Academic Performance among Pharmacy Students. American Journal of Pharmaceutical Education, 70, 1-9.
http://dx.doi.org/10.5688/aj7005104 - 4. Biswas, R. (1995) An Application of Fuzzy Sets in Students’ Evaluation. Fuzzy Sets and System, 74, 187-194.
http://dx.doi.org/10.1016/0165-0114(95)00063-Q - 5. Malvezzi, W.R., Mourao, A.M. and Bressan, G. (2010) Learning Evaluation in Classroom Mediated by Technology Model Using Fuzzy Logic at the University of Amazonas State. Proceeding of 40th ASEE/IEEE Frontiers in Education Conference, Washington DC, 27-30 October 2010, S2C-1-S2C-6.
http://dx.doi.org/10.1109/fie.2010.5673494 - 6. Udoinyang, Inyang, G. and Joshua, E.E. (2013) Fuzzy Clustering of Students’ Data Repository for At-Risks Students Identification and Monitoring. Computer and Information Science, 6, 37-50.
- 7. Gokmen, G., Akinci, T.C., Tekta, M., Onat, N., Kocyigit, G. and Tekta, N. (2010) Evaluation of Student Performance in Laboratory Applications Using Fuzzy Logic. Procedia Social and Behavioral Sciences, 2, 902-909.
http://dx.doi.org/10.1016/j.sbspro.2010.03.124 - 8. Saxena, N. and Saxena, K.K. (2010) Fuzzy Logic Based Students Performance Analysis Model for Educational Institutions. VIVECHAN International Journal of Research, 1, 79-86.
- 9. Neogi, A., Mondal, A.C. and Mandal, S.K. (2011) A Cascaded Fuzzy Inference System for University Non-Teaching Staff Performance Appraisal. Journal of Information Processing Systems, 7, 595-612.
http://dx.doi.org/10.3745/JIPS.2011.7.4.595 - 10. Bhosale, G.A. and Kamath, R.S. (2013) Fuzzy Inference System for Teaching Staff Performance Appraisal. International Journal of Computer and Information Technology, 2, 381-385.
- 11. Boongoen, T., Shen, Q. and Price, C.J. (2011) Fuzzy Qualitative Link Analysis for Academic Performance Evaluation. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 19, 559-585.
http://dx.doi.org/10.1142/S0218488511007131 - 12. Hameed, I.A. (2011) Using Gaussian Membership Functions for Improving the Reliability and Robustness of Students’ Evaluation System. International Journal of Expert System with Applications, 38, 7135-7142.
http://dx.doi.org/10.1016/j.eswa.2010.12.048 - 13. Khan, A.R., Amin, H.U. and Rehman, Z.U. (2011) Application of Expert System with Fuzzy Logic in Teachers’ Performance Evaluation. International Journal of Advanced Computer Science and Applications, 2, 51-57.
- 14. Daud, W.S.W., Aziz, K.A.A. and Sakib, E. (2011) An Evaluation of Students’ Performance in Oral Presentation Using Fuzzy Approach. Proceedings of Universiti Malaysia Terengganu 10th International Annual Symposium on Empowering Science, Technology and Innovation towards a Better Tomorrow, Kuala Terengganu, 11-13 July 2011, 157-162.
- 15. Gangadwala, H. and Gulati, R.M. (2012) Grading & Analysis of Oral Presentation—A Fuzzy Approach. International Journal of Engineering Research and Development, 2, 1-4.
- 16. Bhatt, R. and Bhatt, D. (2011) Fuzzy Logic based Student Performance Evaluation Model for Practical Component of Engineering Institution Subjects. International Journal of Technology and Engineering Education, 5, 1-7.
- 17. Jamsandekar, S.S. and Mudholkar, R.R. (2013) Performance Evaluation by Fuzzy Inference Technique. International Journal of Soft Computing and Engineering, 3, 158-164.
- 18. Patil1, S., Mulla, A. and Mudholkar, R.R. (2012) Best Student Award—A fuzzy Evaluation Approach. International Journal of Computer Science and Communication, 3, 9-12.
- 19. Gangadhar, P.V.S.S. (2012) Evaluation of Government Officer Performance Using Fuzzy Logic Techniques. Indian Journal of Computer Science and Engineering, 3, 319-328.
- 20. Yildiz, O., Bal, A. and Gulsecen, S. (2013) Improved Fuzzy Modelling to Predict the Academic Performance of Distance Education Students. The International Review of Research in Open and Distance Learning, 14, 144-165.
- 21. Yildiz, Q., Bal, A., Gulsecen, S. and Kentli, F.D. (2014) Rules Optimization Based Fuzzy Model for Predicting Distance Education Students’ Grades. International Journal of Information and Education Technology, 4, 59-62.
http://dx.doi.org/10.7763/IJIET.2014.V4.369 - 22. Sakthivel, E., Kannan, K.S. and Arumugam, S. (2013) Optimized Evaluation of Students Performances Using Fuzzy Logic. International Journal of Scientific and Engineering Research, 4, 1128-1133.
- 23. Chang, D.F. and Sun, C.H. (1993) Fuzzy Assessment Learning Performance of Junior High School Students. Proceedings of the 1993 First National Symposium on Fuzzy Theory and Applications, Hsinchu, 1-10.
- 24. Chiang, T.T. and Lin, C.H. (1994) Application of Fuzzy Theory to Teaching Assessment. Proceedings of the 1994 Second National Conference on Fuzzy Theory and Applications, Taipei, 15-17 September 1994, 92-97.
- 25. Law, C.K. (1996) Using Fuzzy Numbers in Education Grading System. Fuzzy Sets and Systems, 83, 311-323.
http://dx.doi.org/10.1016/0165-0114(95)00298-7 - 26. Weon, S. and Kim, J. (2001) Learning Achievement Evaluation Strategy Using Fuzzy Membership Function. Proceedings of the 31st ASEE/IEEE Frontiers in Education Conference, Vol. 1, Reno, 10-13 October 2001, 19-24.
- 27. Gamboa, H. (2001) Designing Intelligent Tutoring Systems: A Bayesian Approach. Proceedings of the 3rd International Conference on Enterprise Information System, Setúbal, 7-10 July 2001, 452-458.
- 28. Hwang, G.J. (2003) A Conceptual Map Model for Developing Intelligent Tutoring Systems. International Journal of Computers and Education, 40, 217-235.
http://dx.doi.org/10.1016/S0360-1315(02)00121-5 - 29. Aziz, A.A., Ismail, N.H. and Ahmad, F. (2013) Mining Students’ Academic Performance. Journal of Theoretical and Applied Information Technology, 53, 485-495.
- 30. Shah, K.N., Kothuru, S. and Vairamuthu, S. (2013) Clustering Students’ Based on Previous Academic Performance. International Journal of Engineering Research and Applications, 3, 935-939.
- 31. Ramanathan, L., Dhanda, S. and Kumar, D.S. (2013) Predicting Students’ Performance using Modified ID3 Algorithm. International Journal of Engineering and Technology, 5, 2491-2497.
- 32. Pandey, M. and Sharma, V.K. (2013) A Decision Tree Algorithm Pertaining to the Student Performance Analysis and Prediction. International Journal of Computer Applications, 61, 1-5.
http://dx.doi.org/10.5120/9985-4822 - 33. Borkar, S. and Rajeswari, K. (2013) Predicting Students Academic Performance Using Education Data Mining. International Journal of Computer Science and Mobile Computing, 2, 273-279.










