Received 15 June 2015; accepted 1 July 2015; published 8 July 2015

ABSTRACT

The homogeneous system of the equations of the linear theory of elasticity for the isotropic environment with one-dimensional continuous heterogeneity is considered. Bidimensional transformation Fourier is applied and the problem for images is led to the ordinary differential equations. Generally, the differential equations are transformed in integro-differential and the algorithm of such transformation is resulted. Solutions of specific problems are resulted.

Keywords:

Continuous Heterogeneity, The Integro-Differential Equation, Bidimensional Fourier’s Transformation

Subject Areas: Geophysics

1. Introduction

The elastic half-space is considered inhomogeneous along depth. Such problems were investigated in many works (for example, [1] - [3] ). The detailed review is not the purpose of this paper, but the technique applied in the paper does not meet in publications. Let’s note that problems for an elastic half-space are especially important in a science about the Earth as the Earth’s crust is usually modelled by a half-space.

Research is made with application of bidimensional transformation Fourier which leads to the ordinary differential equations. The method of transition to integral equations [4] is applied to their solution. Such technique expands a circle of problems for which it is possible to find the satisfactory approached solution. The concrete example is resulted.

2. Statement of the Problem

In cartesian coordinates (x, y, z) it is considered isotropic inhomogeneous on z an elastic half-space z ≥ 0 with the shear modulus μ(z) and coefficient of Poisson ν(z). In this case the homogeneous system of the equations of the theory of elasticity in displacements (u, v, w) looks like

(2.1)

where is a volume strain, ω = 1 − 2ν, Δ is Laplace operator on three variables, the comma in an inferior index means a derivative on corresponding variable.

In [5] it is shown, that the system (2.1) is equivalent to system for two functions

(2.2)

where η = d(lnμ)/dz. β = 1 − ν, Δ_xy is Laplace operator on two variables.

Displacements are expressed by formulas

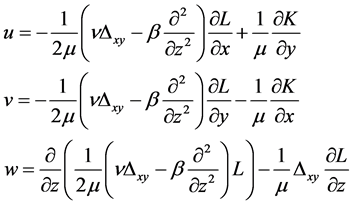(2.3)

and stresses are

. (2.4)

Formulas (2.1)-(2.4) are received in the monograph [5] . Here it have undergone to some transformations.

To a half-space (or a lay) we shall apply bidimensional transformation Fourier in the form of

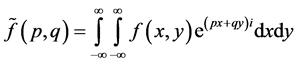(2.5)

where i is imaginary unit.

Then the basic operators will be transformed by formulas

. (2.6)

For functions and the system (2.2) gets an aspect

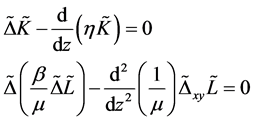. (2.7)

Transformations of stresses on a plane z = const are

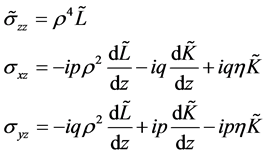. (2.8)

The problem is reduced to a solution of the ordinary linear differential equations for functions 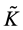and 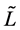with corresponding boundary conditions. The reversion of transformation of Fourier (calculation of definite integrals) does not cause difficulties for modern mathematical programs.

3. The Equation for

The first equation from (2.7) we will write down in a kind

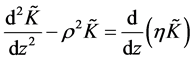. (3.1)

One of ways of search of the approached the general solution of the Equation (3.1) for any smooth function μ(z) is transition to the integro-differential equation on algorithm [4] . In so doing an operator is chosen by the basic operator, because for a homogeneous environment (μ = const) the Equation (3.1) has form.

For a finite segment we use the general solution of the inhomogeneous equation. The homogeneous equation has a Green function limited on infinity [6]

. (3.2)

It allows to construct the equation for a semi-infinite segment.

As a result we come to two integro-differential equations of the II kind:

for layer

(3.3)

and for a half-space

. (3.4)

By integration by parts (3.3) and (3.4) will be transformed to integral equations

, (3.5)

. (3.6)

If for the equation it is possible to construct a Green function for the chosen boundary conditions, then for Equation (3.1) corresponding integral equations are possible to construct for these conditions with its help. Equation (3.4) is an example.

4. The Equation for

Let’s note the second equation of system (2.7) in the form

, (4.1)

where.

If to apply to the Equation (4.1) operator, inverse to, (as it is made in the previous section) then we receive two integral equations:

For a layer

(4.2)

And for a half-space

. (4.3)

At μ = 1/(az+b) function Q(z) = 0 and Formulas (4.2) and (4.3) give the exact general solution of the equation (4.1).

5. Solution of the Specific Problem

We shall consider a problem about unit force on a surface of a half-space z ≥ 0 in the origin of coordinates. Apparently from system (2.8), in this case (and, in general, for problems with axial symmetry) it is possible to put = 0. For function boundary conditions receive the form

. (5.1)

Let’s put

. (5.2)

Then the Equation (4.1) has the solution limited on infinity

. (5.3)

Here C₁ and C₂ are arbitrary constants, ζ = ρ(1 + z), Ψ(α, β; x) is degenerate hypergeometric function of 2-nd sort or Kummer’s function of 2-nd kind. In computer program Maple this function is designated as Kummer U (α, β, z) and it has integral representation

(5.4)

where Γ(a) is the gamma-function.

It is simple to receive the solution of the problem (5.1)-(5.3) in Fourier transformations, but to carry out the inverse Fourier transform through known functions is not receive. However it is possible to approximate special functions by combinations of elementary functions. Approximation can be made with a demanded exactitude and simplifies the further calculations. In particular for (5.3) we have

. (5.5)

The error of this approximation does not exceed 0.5 %.

Level lines of stress σ_zz are shown on Figure 1. The narrow layer at the half-space surface is empty because it is necessary to show it in larger scale though qualitative behaviour of level lines in this layer to present simply. Existence of a zone of small tensile stresses is the basic singularity of this graph. In a homogeneous half-space

(the Boussinesq’s problem) such zone does not arise.

It is interesting to compare the received solution to the approximate solution. As the approximate solution we take the zero approximation for the Equation (4.3). Such solution turns out at Q = 0 and it has the form

. (5.6)

Using boundary conditions (5.1) we receive function

. (5.7)

According to (2.8) transformation of stress σ_zz gets the form

. (5.8)

To receive stress σ_zz it is necessary to calculate integral

, (5.9)

where and is Bessel’s function.

To calculate (5.9) we will allocate the whole part in the integrand.

. (5.10)

The integral (5.9) is calculated in elementary functions for first three items from a right part of (5.10). The fourth item leads to the integral

, (5.11)

which is not expressed in known functions.

However by means of approximation

(5.12)

integral (5.11) also can be calculated in elementary functions. This operation is easily supervised because the integral (5.11) can be found in separate points numerically by means of known mathematical programs (for example, Maple or Mathematica).

Level lines of stress σ_zz calculated by the described algorithm are shown on Figure 2. Figure 1 and Figure 2

basically are similar. In the approximate solution the area of small tensile stresses remains but it becomes more extensive and moves further from an origin of coordinates.

6. Conclusion

Transition to integro-differential (or integral) equations is an effective method of a solution of problems for a half-space (or a layer) with arbitrary heterogeneity. It is very important that the solution of an integral equation gives the approximate general solution of the ordinary differential equation. Procedure of transition to integro- differential (or integral) equations allows constructing such equations for the inhomogeneous differential equations.

Cite this paper

Igor Petrovich Dobrovolsky, (2015) Unidimensional Inhomogeneous Isotropic Elastic Half-Space. Open Access Library Journal,02,1-6. doi: 10.4236/oalib.1101670

References