Open Access Library Journal
Vol.02 No.07(2015), Article ID:68482,6 pages
10.4236/oalib.1101345
Of a Fatigued Thick-Walled Cylindrical Pipe on the Brink of Yielding
Nzerem Francis Egenti
Department of Mathematics and Statistic, University of Port Harcourt, Port Harcourt, Nigeria
Email: frankjournals@yahoo.com
Copyright © 2015 by author and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 14 June 2015; accepted 30 June 2015; published 7 July 2015

ABSTRACT
The response to stress delivered by a non-isochoric hollow cylinder is critical to its future life and integrity. The design of cylinders must emphasize durability; therefore, the knowledge of the yield stress of the constituent material is essential. The stress component of a pressurized compressible circular cylinder made of non-linearly elastic material was considered here and the yield stress was determined.
Keywords:
Compressible, Pressure, Deformation Tensor, Elasto-Plastic Material, Strain
Subject Areas: Continuum Mechanics

1. Introduction
Numerous literatures have considered stress onaxisymmetrically pressurized cylinders. When internally pressurized hollow circular cylinder is being considered, it is customary to assume that the cylinder has to contend with radial, hoop (circumferential) and axial stresses. The magnitude of the response to stress is related to the material constitution of the cylinder. In recent times several works [1] - [3] have considered the elasto-plastic materials as being able to meet the exigencies of modern times. The recourse to the elasto-plastic approach may be borne out of the relative availability and cost effectiveness of the plastic component. This approach is, however, not a paradigm shift from completely elastic materials.
The works done by Blatz and Ko [4] , Chung et al. [5] , Hills and Ariggo [6] dealt on materials of nonlinear elasticity. The question of stress-induced fatigue is a sine qua non for the design of conduit pipes. Although static response to stress immanent in materials accounts for the life span and integrity of pipes, relative longevity resides in those made of materials of (non-)linear elasticity, all else being equal. The need to increase the life span of conduits dominates every argument. It is this need that gives rise to the autofrettage process being adopted in present times. The process applies a sufficiently high pressure to the cylinder before it is put in use. The withdrawal of the internally applied pressure induces a residual stress on the part of the cylinder thickness which has become plastic. This would in effect help the cylinder to cushion the effect of high pressures in event of use. This process means well for elasto-plastic cylinders. It is gaining currency, as can be seen in literatures [1] [7] [8] . In any case, repeated or prolonged stress is usually implicated in material fatigue. Fatigue is a grave engineering liability, together with its attendant economic implications. The aforesaid underscores the need to determine the measure of stress applicable to a cylindrical medium under consideration. This paper therefore presented a theoretical formulation of pressure limits of a thick-walled cylinder, made of a non-linearly elastic material. This was done in the following order: Section 2 proposed the model of an axially symmetric hollow cylinder, of Blatz-Ko material, subjected to plane strain. The Cauchy-Green deformation tensors were used in determining the components of stress on the cylinder. Section 3 formulated a boundary-value problem (b.v.p) in which pressure p accounted for the radial stress in the cylinder. The emerging equation, together with boundary conditions, was transformed with the aid of a suitable transformation equation (see Equation (21)). The transformation successfully linearized the boundary conditions and facilitated the solution to the b.v.p. In event of this, the components of stress, with pressure content, were determined. Section 4 furnished the yield criterion. It supplied the critical stresses with the aid of Tresca yield criterion. Previous literatures may have sought a compact expression for the yield stress on the material under consideration; perhaps this is the missing link.
2. Deformation of the Cylinder
We consider a hollow cylinder whose reference configuration is
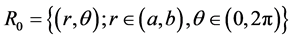 (1)
(1)
where a is the inner radius and b is the outer radius of the cylinder. Its deformed configuration is given by the mapping
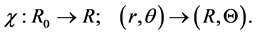 (2)
(2)
For this axisymmetric plane strain, it suffices to assume that R(r) is twice continuously differentiable, and we write
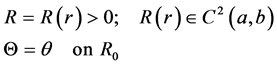 (3)
(3)
The deformation gradient tensor F associated with (3) is
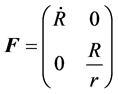 (4)
(4)
where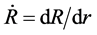 . The tensor F is required to satisfy the non-singularity condition by virtue of the local invertibility of χ. Moreover, we suppose detF > 0. The assumption of the existence of strain at some point X Î Ro ensues that
. The tensor F is required to satisfy the non-singularity condition by virtue of the local invertibility of χ. Moreover, we suppose detF > 0. The assumption of the existence of strain at some point X Î Ro ensues that
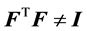 , (5)
, (5)
where I is the identity tensor, the superscripted T indicates the transpose of F. (Note that X are position vectors of points in Ro). A class of materials under consideration is characterized by the strain energy density function W(I, J), whose related Blatz-Ko model is given by [5]
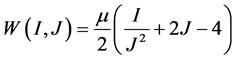 (6)
(6)
where μ is the initial shear modulus of the material. The function W is just one among the scalar functions of strain tensors used in determining stress components. In terms of the second Piola-Kirchhoff’s (PK-2) stress tensor Sij, we have
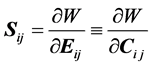 (7)
(7)
where Sij is the component of the PK-2 stress tensor, W is the strain energy function per unit undeformed volume, Eij is the component of the Lagrangean strain tensor and Cij is the Cauchy-Green deformation tensor.
The associated right Cauchy-Green deformation tensors is
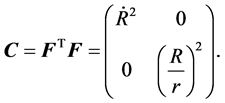 (8)
(8)
With the invariants, I and J as
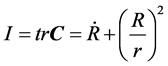
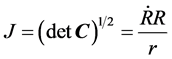 . (9)
. (9)
With the principal stretches
 (10)
(10)
The stress tensor σ associated with this deformation is given by
 (11)
(11)
where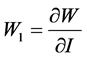 ,
, 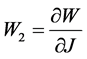 and I is the identity tensor.
and I is the identity tensor.
From Equation (6) we get
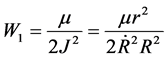 (12)
(12)
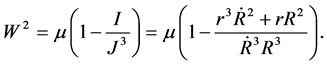 (13)
(13)
Using equation (8), (12) and (13) in (11) we get the following stress component



3. Boundary-Value Problem
When uniform pressure is applied at the boundaries, the circumferential component of displacement is zero, and the radial component will depend on the radial distance r only. The stress components will therefore depend on r only. If body force is absent, the equilibrium equation is given by

Using Equations (14) and (15) in Equation (17) we get the equation for R(r) as

with the constraints

The Equations (19) may be rewritten, using (14) and (15), as

We apply the transformation similar to Ejike and Erumaka [9] , (also see [10] [11] )

Equation (18) becomes

and the line arized boundary conditions (20) are


The series solution approach of the form

was employed rigorously by Nzerem [11] which yielded

where

The resulting stress components are


4. Yield Criterion
Yielding becomes imminent when the maximum shear stress in the material equals the maximum shear stress. Thus, Tresca yield criterion [12] specifies that

where

σmax and σmin are the maximum and minimum principal stresses respectively. From the foregoing we get

Thus, we get

where

Equations (33) and (34) contain pressure (see Equation (27)); therefore, the non-dimensionalized inner and outer surface pressure limit can be obtained by solving for p.
5. Conclusion
The need to ascertain the fatigue point of a thick-walled cylinder under stress is crucial in estimating the life span of the cylinder. The stress component must be known before determining the yield stress. In this work, the stress component was determined. The cylinder under consideration was made of compressible non-linearly elastic (Blatz-Ko) material. The yield stress was determined with the aid of Tresca criterion.
Acknowledgements
The author is grateful to the reviewers of this paper for their useful comments.
Cite this paper
Nzerem Francis Egenti, (2015) Of a Fatigued Thick-Walled Cylindrical Pipe on the Brink of Yielding. Open Access Library Journal,02,1-6. doi: 10.4236/oalib.1101345
References
- 1. Ayob, A.B., Tamin, M.N. and Elbasheer, M.K. (2009) Pressure Limits of Thick-Walled Cylinders. Proceedings of the International Multi-Conference of Engineers and Computer Scientists 2009, Vol. II IMECS, 18-20 March 2009.
- 2. Wang, Z. (1995) Elastic-Plastic Fracture Analysis of a Thick-Walled Cylinder. International Journal of Pressure Vessels and Piping, 63, 165-168.
http://dx.doi.org/10.1016/0308-0161(94)00048-N - 3. Chaaban, A. and Barake, N. (1993) Elasto-Plastic Analysis of High Pressure Vessels with Radial Cross Bores. High Pressure Technology, 263, 67-123.
- 4. Blatz, P.D. and Ko, W.L. (1962) Application of Finite Elasticity to the Deformation of Rubbery Materials. Transactions of the Society of Rheology, 6, 223-251.
http://dx.doi.org/10.1122/1.548937 - 5. Chung, D.T., Horgan, C.O. and Abeyaratne, R. (1986) The Finite Deformation of Internally Pressurized Hollow Cylinders and Spheres for a Class of Compressible Elastic Materials. International Journal of Solids and Structures, 22, 1557-1570.
http://dx.doi.org/10.1016/0020-7683(86)90062-4 - 6. Hills, J.M. and Arrigo, D.J. (1996) On Axially Symmetric Deformation of Perfectly Elastic Compressible Material. Quarterly Journal of Mechanics Applied Mathematics, 49, 19-28.
http://dx.doi.org/10.1093/qjmam/49.1.19 - 7. Perry, T. and Aboudi, J. (2003) Elastic-Plastic Stresses in Thick-Walled Cylinders. Journal of Pressure Vessel Technology, 125, 248.
http://dx.doi.org/10.1115/1.1593078 - 8. Zhao, W., Seshadri, R. and Dubey, R.N. (2003) On Thick-Walled Cylinder under Internal Pressure. Journal of Pressure Vessel Technology, 125, 267-273.
http://dx.doi.org/10.1115/1.1593082 - 9. Ejike, U.B.C.O. and Erumaka, E.N. (2006) Finite Deformation of Rotating Circular Cylinder of Blatz-Ko Material. Journal of Mathematical Sciences, 17, 63-71.
- 10. Nzerem, F.E. (2007) The Component of Stress on an Internally Pressurized Circular Cylinder of the Blatz-Ko Material. Research Journal of Applied Sciences, 2, 420-423.
- 11. Nzerem, F.E. (2007) Stresses Resulting from Fluid Flow in Pipes. M.Sc. Thesis, Federal University of Technology, Owerri.
- 12. Andri, A. (2008) Failure Criteria for Yielding.
http://andriandriyana.files.wordpress.com/2008/03/yield_criteria.pdf


