Open Access Library Journal
Vol.02 No.06(2015), Article ID:68463,7 pages
10.4236/oalib.1101620
Special Matrices in Constructing Mutually Unbiased Maximally Entangled Bases in 
Jun Zhang, Qiang Yang, Hua Nan, Yuanhong Tao*
Department of Mathematics, College of Sciences, Yanbian University, Yanji, China
Email: *taoyuanhong12@126.com
Copyright © 2015 by authors and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 2 June 2015; accepted 20 June 2015; published 25 June 2015

ABSTRACT
Some special matrices can really help us to construct more than two mutually unbiased maximally entangled bases in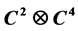 . Through detailed analysis of the necessary and sufficient conditions of two maximally entangled bases to be mutually unbiased, we find these special matrices. Taking one such kind of matrix, we present the steps of constructing five mutually unbiased maximally entangled bases in
. Through detailed analysis of the necessary and sufficient conditions of two maximally entangled bases to be mutually unbiased, we find these special matrices. Taking one such kind of matrix, we present the steps of constructing five mutually unbiased maximally entangled bases in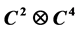 .
.
Keywords:
Maximally Entangled States, Mutually Unbiased Bases, Pauli Matrices
Subject Areas: Algebra, Quantum Mechanics, Theoretical Physics

1. Introduction
Mutually unbiased maximally entangled bases (MUMEBs) are an interesting topic combining mutually unbiased bases (MUBs) and maximally entangled states. Mutually unbiased bases play an central role in quantum kinematics [1] , quantum state tomography [2] - [4] and many tasks in quantum information processing, such as quantum key distribution [5] , cryptographic protocols [6] [7] , mean king problem [8] , quantum teleportation and superdense coding [9] - [11] . Maximally entangled state is central both to the foundations of quantum mechanics and to quantum information and computation [12] - [24] .
A state 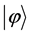 is said to be a
is said to be a 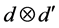 (
(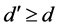 ) maximally entangled state if and only if for an arbitrary given orthonormal complete basis
) maximally entangled state if and only if for an arbitrary given orthonormal complete basis  of subsystem A, there exists an orthonormal basis
of subsystem A, there exists an orthonormal basis  of subsystem B such that
of subsystem B such that 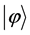 can be written as
can be written as 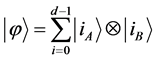 [24] . Two orthonormal bases
[24] . Two orthonormal bases 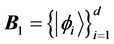 and
and 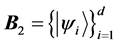 of
of  are mutually unbiased if and only if
are mutually unbiased if and only if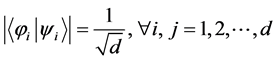 . A set of
. A set of
orthonormal bases 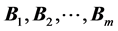 in
in 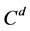 are said to be a set of mutually unbiased bases if every pair of bases in the set is mutually unbiased.
are said to be a set of mutually unbiased bases if every pair of bases in the set is mutually unbiased.
Mutually unbiased bases are recently combined with other bases, such as product basis (PB) [25] , unextendible product basis (UPB) [26] , unextendible maximally entangled basis (UMEB) [27] - [32] and maximally entangled basis (MEB) [33] - [35] . The MEB is a set of orthonormally maximally entangled states in 

MUMEBs in bipartite systems 
In this note, we study the problem of constructing more than two mutually unbiased maximally entangled bases in bipartite spaces

2. Main Results
We first recall the sufficient and necessary conditions of two maximally entangled bases to be mutually unbiased in
Let 







We first consider two MEBs in 


where 

From [33] , the above two MEBs (1) and (2) in 

where 


To visualize the conditions (3), we divide the transition matrix A into 4 submatrices of 2 × 2 from left to right, then the conditions (3) hold if and only if each 2 × 2 submatrix satisfying the similar conditions as follows (we might take the upper left submatrix as a representative):

From [33] , it is easy to find matrices satisfying the above conditions (4) such as
In this note, we want to find more than two MUMEBs, so how to find the third MEB mutually unbiased with the above two MEBs (1) and (2), it depends on the property transit matrix satisfied. Suppose that







cording to [33] , we have the third MEB as follows

Then, the above three MEBs in 
Since the transit matrix A is easy to choose, we really want to know the way to construct matrix B. Assume that
where P is a 2 × 2 matrix, if A is known, how can we choose the matrix P to assure B and BA all satisfy the conditions (4)? For simplicity, we can first assume that P be a diagonal block matrix

then we have

Since B satisfy the conditions (4), then we have

thus we must have
It follows from the unitarity of matrix P that

Similarly, we can have

so there are many choices about the values of


We first discuss the case I. Obviously, there are many forms of P satisfying the above property, such as

No loss of generality, we first choose

then we have
It is direct to verify that the transformation matrix B and BA both satisfy the conditions (4), then the MEBs (1), (2) and (5) in 
Let
Denoting 





structed as follows:

Obviously, 

It is easy to check the above matrices C, 


Moreover, let
Denoting 







Obviously, 


One can directly check that the above matrices




Furthermore, let
Denoting 






Since 


Next, we discuss Case II of
If we take the same A in (12) and choose the following form of P:
similar to the above analysis, we can get the five MUMEBs in 
3. Conclusion
In this note, we have constructed five mutually unbiased maximally entangled bases in bipartite spaces 


Cite this paper
Jun Zhang,Qiang Yang,Hua Nan,Yuanhong Tao, (2015) Special Matrices in Constructing Mutually Unbiased Maximally Entangled Bases in C C4. Open Access Library Journal,02,1-7. doi: 10.4236/oalib.1101620
C4. Open Access Library Journal,02,1-7. doi: 10.4236/oalib.1101620
References
- 1. Durt, T., Englert, B.-G., Bengtsson, I. and Zyczkowski, K. (2010) On Mutually Unbiased Bases. International Journal of Quantum Information, 8, 535.
http://dx.doi.org/10.1142/S0219749910006502 - 2. Ivanovic, I.D. (1981) Geometrical Description of Quantal State Determination. Journal of Physics A: Mathematical and General, 14, 3241.
http://dx.doi.org/10.1088/0305-4470/14/12/019 - 3. Wootters, W.K. and Fields, B.D. (1989) Optimal State-Determination by Mutually Unbiased Measurements. Annals of Physics, 191, 363-381.
http://dx.doi.org/10.1016/0003-4916(89)90322-9 - 4. Englert, B.-G., Kaszlikowski, D., Kwek, L.C. and Chee, W.H. (2008) Wave-Particle Duality in Multi-Path Interferometers: General Concepts and Three-Path Interferometers. International Journal of Quantum Information, 6, 129-157.
- 5. Cerf, N.J., Bourennane, M., Karlsson, A. and Gisin, N. (2002) Security of Quantum Key Distribution Using d-Level Systems. Physical Review Letters, 88, Article ID: 127902.
http://dx.doi.org/10.1103/PhysRevLett.88.127902 - 6. Xiong, Z.-X., Shi, H.-D., Wang, Y.-N., Jing, L., Lei, J., Mu, L.-Z. and Fan, H. (2012) General Quantum Key Distribution in Higher Dimension. Physics Review A, 85, Article ID: 012334.
- 7. Brierley, S. (2009) Quanturn Key Distribution Highly Sensitive to Eavesdropping. arXiv: 0910.2578.
- 8. Aharonov, Y. and Englert, B.G. (2001) The Mean King’s Problem: Spin 1. Zeitschrift Fur Naturforsch, 56a, 16.
- 9. Durt, T. (2004) e-pnnt arXiv: quant-ph/0401046.
- 10. Klimov, A.B., Sych, D., Sanchez-Soto, L.L. and Leuchs, G. (2009) Mutually Unbiased Bases and Generalized Bell States. Physical Review A, 79, Article ID: 052101.
http://dx.doi.org/10.1103/PhysRevA.79.052101 - 11. Revzen, M. (2010) Maximally Entangled States via Mutual Unbiased Collective Bases. Physical Review A, 81, Article ID: 012113.
http://dx.doi.org/10.1103/PhysRevA.81.012113 - 12. Vedral, V. (2002) The Role of Relative Entropy in Quantum Information Theory. Reviews of Modern Physics, 74, 197-234.
http://dx.doi.org/10.1103/RevModPhys.74.197 - 13. Plenio, M.B. and Virmani, S. (2007) An Introduction to Entanglement Measures. Quantum Information and Computation, 7, 1-51.
- 14. Horodecki, R., Horodecki, P., Horodecki, M. and Horodecki, K. (2009) Quantum Entanglement. Reviews of Modern Physics, 81, 865-942.
http://dx.doi.org/10.1103/RevModPhys.81.865 - 15. Benhelm, J., Kirchmair, G., Roos, C.F. and Blatt, R. (2008) Towards Fault-Tolerant Quantum Computing with Trapped Ions. Nature Physics, 4, 463-468.
http://dx.doi.org/10.1038/nphys961 - 16. Bennett, C.H., Brassard, G., Crepeau, C., Jozsa, R., Peres, A. and Wootters, W.K. (1993) Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels. Physical Review Letters, 70, 1895-1899.
http://dx.doi.org/10.1103/PhysRevLett.70.1895 - 17. Zhang, Q., Goebel, A., Wagenknecht, C., Chen, Y.A., Zhao, B., Yang, T., Mair, A., Schmied-Mayer, J. and Pan, J.W. (2006) Experimental Quantum Teleportation of a Two-Qubit Composite System. Nature Physics, 2, 678-682.
http://dx.doi.org/10.1038/nphys417 - 18. Modlawska, J. and Grudka, A. (2008) Non-Maximally Entangled States Can Be Better for Multiple Linear Optical Teleportation. Physical Review Letters, 100, Article ID: 110503.
http://dx.doi.org/10.1103/PhysRevLett.100.110503 - 19. Ishizaka, S. and Hiroshima, T. (2009) Quantum Teleportation Scheme by Selecting One of Multiple Output Ports. Physical Review A, 79, Article ID: 042306.
http://dx.doi.org/10.1103/PhysRevA.79.042306 - 20. Noh, C., Chia, A., Nha, H., Collett, M.J. and Carmichael, H.J. (2009) Quantum Teleportation of the Temporal Fluctuations of Light. Physical Review Letters, 102, Article ID: 230501.
http://dx.doi.org/10.1103/PhysRevLett.102.230501 - 21. Bennett, C.H. and Wiesner, S.J. (1992) Communication via One- and Two-Particle Operators on Einstein-Podolsky-Rosen States. Physical Review Letters, 69, 2881-2884.
http://dx.doi.org/10.1103/PhysRevLett.69.2881 - 22. Barreiro, J.T., Wei, T.C. and Kwiat, P.G. (2008) Beating the Channel Capacity Limit for Linear Photonic Superdense Coding. Nature Physics, 4, 282-286.
http://dx.doi.org/10.1038/nphys919 - 23. Bennett, C.H. and Di Vincenzo, D.P. (2000) Quantum Information and Computation. Nature, 404, 247-255.
http://dx.doi.org/10.1038/35005001 - 24. Li, Z.G., Zhao, M.J., Fei, S.M., Fan, H. and Liu, W.M. (2012) Mixed Maximally Entangled States. Quantum Information & Computation, 12, 63-73.
- 25. McNulty, D. and Weigert, S. (2012) The Limited Role of Mutually Unbiased Product Bases in Dimension 6. Journal of Physics A: Mathematical and Theoretical, 45, Article ID: 102001.
http://dx.doi.org/10.1088/1751-8113/45/10/102001 - 26. Bennett, C.H., Divincenzo, D.P., Mor, T., Shor, P.W., Smolin, J.A. and Terhal, B.M. (1999) Unextendible Product Bases and Bound Entanglement. Physical Review Letters, 82, 5385-5388.
http://dx.doi.org/10.1103/PhysRevLett.82.5385 - 27. Bravyi, S. and Smolin, J.A. (2011) Unextendible Maximally Entangled Bases. Physical Review A, 84, Article ID: 042306.
http://dx.doi.org/10.1103/PhysRevA.84.042306 - 28. Chen, B. and Fei, S.M. (2013) Unextendible Maximally Entangled Bases and Mutually Unbiased Bases. Physical Review A, 88, Article ID: 034301.
http://dx.doi.org/10.1103/PhysRevA.88.034301 - 29. Nan, H., Tao, Y.H., Li, L.S. and Zhang, J. (2014) Unextendible Maximally Entangled Bases and Mutually Unbiased Bases in ℂd ⊗ ℂd′. International Journal of Theoretical Physics, 54, 927-932.
http://dx.doi.org/10.1007/s10773-014-2288-1 - 30. Li, M.S., Wang, Y.L. and Zheng, Z.J. (2014) Unextendible Maximally Entangled Bases in ℂd ⊗ ℂd′. Physical Review A, 89, Article ID: 062313.
http://dx.doi.org/10.1103/PhysRevA.89.062313 - 31. Wang, Y.L., Li, M.S. and Fei, S.M. (2014) Unextendible Maximally Entangled Bases in ℂd ⊗ ℂd′. Physical Review A, 90, Article ID: 034301.
http://dx.doi.org/10.1103/PhysRevA.90.034301 - 32. Nizamidin, H., Ma, T. and Fei, S.M. (2014) A Note on Mutually Unbiased Unextendible Maximally Entangled Bases in C2 ⊗ C3. International Journal of Theoretical Physics, 54, 326-333.
http://dx.doi.org/10.1007/s10773-014-2227-1 - 33. Tao, Y.H., Nan, H., Zhang, J. and Fei, S.M. (2015) Mutually Unbiased Maximally Entangled Bases in Cd ⊗ Ckd. Quantum Information Processing, 14, 2291-2300.
http://dx.doi.org/10.1007/s11128-015-0980-6 - 34. Zhang, J., Tao, Y.H., Nan, H. and Fei, S.M. (2015) Construction of Mutually Unbiased Bases in Cd ⊗ C2ld′. Quantum Information Processing, 14, 2635-2644.
http://dx.doi.org/10.1007/s11128-015-0961-9 - 35. Tao, Y.H., Yang, Q., Zhang, J., Nan, H. and Li, L.S. (2015) The Concrete Construction of Mutually Unbiased Maximally Entangled Bases in Cd ⊗ Ckd. Scientia Sinica Physica, Mechanica & Astronomica, 45, Article ID: 060302.
http://dx.doi.org/10.1360/SSPMA2015-00056
NOTES
*Corresponding author.















