Received 25 May 2015; accepted 12 June 2015; published 23 June 2015

ABSTRACT

Initial value ordinary differential equations arise in formulation of problems in various fields such as physics and Engineering. The present paper shows the method how to solve the initial value ordinary differential equation on some interval by using finite difference method in a very accurate manner with the formulation of error estimation.

Keywords:

Ordinary Differential Equation, Finite Difference Method, Interpolation, Error Estimation

Subject Areas: Mathematical Analysis, Ordinary Differential Equation

1. Introduction

Differential equations are used to model problems in science and engineering that involve the change of some variable with respect to the other. Most of these problems require the solution of an initial-value problem, that is, the solution to a differential equation that satisfies a given initial condition. In common real-life situations, the differential equation that models the problem is too complicated to solve exactly [1] . There are numerical methods which simplify such problems and the one is finite difference method which is a numerical procedure that solves a differential equation by discrediting the continuous physical domain into a discrete finite difference grid [2] . Finite difference methods are very suitable when the functions being dealt with are smooth and the differences decrease rapidly with increasing orderas discussed by Colletz, L. [3] : calculations with these methods are best carried out with fairly small length of step. Suppose that the first order IV differential equation

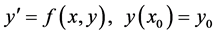(1.1)

is integrated numerically by dividing the interval 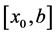on which the solution is desired, into a finite number of sub intervals

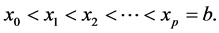
The points are called mesh points or grid points. The spacing between the points is given by

If the spacing is uniform, then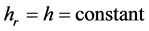,. For this discussion, consider the case of uniform mesh only. Let the range of integration be covered by the equally spaced points 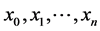with the constant difference 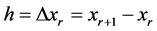(the step length) and let 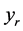be an approximation to the value 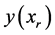of the exact solution at the point. The finite difference methods are based on the integrated form

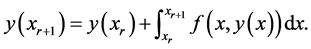(1.2)

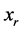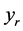That is obtained by integrating Equation (1.1) in the interval then the aim of the finite difference method is to approximate this integral more accurately. Let denote the numerical solution and the exact solution at by and 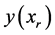respectively. Suppose that the integration has already been carried as far as the point so that approximations and hence also approximate values, are known. The aim is to calculate.

Since cannot be integrated without knowing, which is the solution to the problem, instead integrate an interpolating polynomial, determined by some of the previously obtained data points

. Assuming, in addition, and, then,

(1.3)

This takes the values at a certain number of points and then integrates this polynomial over the interval to. We need to have a sequence of approximations. If the solution at any point is obtained using the solution at only the previous points, then the method is called an explicit method. If the right hand side of (1.2) depends on also, then it is called an implicit method. According to [4] , a general p-step explicit method can be written as

And a general p-step implicit method can be written as

The objective of finite difference method for solving an ordinary differential equation is to transform a calculus problem to an algebra problem [5] . Consequently the finite-difference methods consist of two distinct stages:

I) Approximations, the “starting values” (we reserve the “initial values” for values at the initial point) sufficiently many to calculate the values required for the first application of the finite difference formula, are obtained by some other means.

II) The solution is continued step by step by the finite-difference formulae; these give the values of y at the point once the values at are known “main calculation”.

The approximate solution in finite difference method is converging to the true solution (convergence). If

satisfies the Lipschitz condition i.e.. L being a constant, then the se-

quence of approximations to the numerical solution converges to the exact solution [6] . A finite difference method is convergent if the numerical solution approaches the exact solution as.

2. Calculation of Starting Values

The starting values needed for the main calculation can be obtained in a variety of ways. Particular care must be exercised in the calculation of these starting values, for the whole calculation can be rendered useless by inaccuracies in them. Several possible ways of obtaining starting values are mentioned below:

2.1. Using Some Other Method of Integration

Provided that it is sufficiently accurate, any method of integration which does not require starting values (as distinct from initial values) can be used. Bearing in mind the high accuracy desired, one would normally choose the Runge-Kutta method: further one would work preferably with a step of half the length to be used in the main calculation and with a great number of decimals.

2.2. Using the Taylor Series for y(x)

If the function is of simple analytical form, the derivatives can determined by differentiation of the differential equation; starting values can be calculated from the Taylor series

(1.4)

of which as many terms are taken as are necessary for the truncation not to affect the last decimal carried (always assuming that the series converges).Several of the finite difference methods needs three starting values, and for these it suffices to use (1.4) for; this usually posses advantages over using (2.4) for v =1, 2, particularly as regards convergence.

2.3. Using Quadrature Formulae

Using the forward difference relation, we have

⤇

Here the procedure which is suitable for the construction of two or three starting values can be given. The procedure is completely described by the following formulae.

1), consequently

2)

Again we have the following formulae

⤇ From these there is also

3),

Improving these, the following three starting values can be obtained as;

4)

5)

(1.6)

Generally for (or)

(1.7)

Thus alternatively three y values can be improved and the function values can be revised. and their differences. This starting process should be carried out with a sufficiently small step length.

3. Formulae for the Main Calculation

The next approximate value can be obtained once the values at the points have been computed. To do this the following methods are used.

3.1. The Adams Extrapolation Method

In the extrapolation methods we consider first the function is reduced by the interpolation poly-

nomial P(x) which takes the values at the points [where]. In effect the integral can be evaluated and with and replacing and, (1.1) becomes

(1.8)

The exact solution satisfies the corresponding exact form

(1.9)

where is the remainder term and it is estimated by integrating Newton forward interpolation formula for, we have the following.

3.2. The Adams Interpolation Method

Here the integrand in the Equation (1.1) is replaced by the polynomial P^*(x) which takes the values at the points then from the quadrator formula, it follows that

(1.10)

For the exact solution y(x) we have the following formula

(1.11)

With the remainder term, for which an estimate is given by

3.3. Central Difference Interpolation Method

If we integrate both sides of Equation (1.3) over the interval to, using Stirling’s interpolation formula, we obtain (with p even)

In the remainder term is neglected, the approximations, is

(1.12)

Usually this formula is truncated after the term in, which gives Simpson’s rule:

(1.13)

An estimate for the remainder term in the corresponding formula

(1.14)

for the exact solution the remainder term is calculated as

4. Recursive Error Estimates

This section describes how error is estimated for the finite difference methods. Care must be taken that the number of decimals carried in the calculation is sufficient for rounding errors to be neglected.

I) Taylor series method: If the necessary starting values are calculated by Taylor series method, the error can

usually be estimated very easily; the maximum rounding error, i.e. for a d decimal number, will often provide a suitable upper bound [7] .

II) Quadrature formulae: If the iteration method quadrature formula (1.6) is used to obtain the starting values, the error can be estimated as follows. For the exact solution we have

(1.15)

In which there is have the from at three points (p = 3)

(1.16)

Similarly,

, (1.17)

III) Adams interpolation method: Let us investigate the Adams interpolation method, which is based on the formula (1.11).

A similar relation, but with a remainder term, holds for the exact solution

The truncation error is then

For this remainder term, or “truncation error”, there exists the estimate

5. Conclusion

In this research, finite difference approximate methods for solving initial value ordinary differential equation have been studied. Even if the method is long, it is shown that finite difference method is fundamental to get very accurate solution. Basically the solution method is based on Equation (1.2) by some rearrangement of Equation (1.1). Finite-difference methods are very suitable when the functions being dealt with are smooth and the differences decrease rapidly with increasing order; calculations with these methods are best carried out with a fairly small length of step. On the other hand, if the functions are not smooth, perhaps given by experimental results, or if we want to use a large step, then the Runge-Kutta method is to be preferred; it is also advantageous to use this method when we have to change the length of step frequently, particularly when this change is a decrease. Clearly we should not choose too large a step even for the Runge-Kutta method.

Cite this paper

Negesse Yizengaw, (2015) Numerical Solutions of Initial Value Ordinary Differential Equations Using Finite Difference Method. Open Access Library Journal,02,1-7. doi: 10.4236/oalib.1101614

References