Open Access Library Journal
Vol.02 No.05(2015), Article ID:68406,8 pages
10.4236/oalib.1101507
Classification and Novel Class Detection in Data Streams Using Strings
Rimjhim Singh1, Manoj B. Chandak2
1CSE Department, SRCOEM, Nagpur, India
2CSE Department, Nagpur, India
Email: rimjhimsingh1012@gmail.com, chandakmb@gmail.com
Copyright © 2015 by authors and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 May 2015; accepted 21 May 2015; published 28 May 2015
ABSTRACT
Data streams are continuous and always keep evolving in nature. Because of these reasons it becomes difficult to handle such data with simple and static strategies. Data stream poses four main challenges to researchers. These are infinite length, concept-evolution, concept-drift and feature evolution. Infinite-length is because of the amount of data having no bounds. Concept-drift is due to slow changes in the concept of stream. Concept-evolution occurs due to presence of unknown classes in data. Feature-evolution is because of new features continuously keeping appearing in the stream and older ones start disappearing. For performing any analysis on such data we first need to convert it into some knowledgeable form and also need to handle the above mentioned challenges. Various strategies have been proposed to tackle these difficulties. But most of them focus on handling the problem of infinite-length and concept-drift. In this paper, we make efforts to propose a string based strategy to handle infinite-length, concept-evolution and concept-drift.
Keywords:
Data Stream, Data Mining, Concept-Drift, Concept-Evolution, Novel, Features
Subject Areas: Big Data Search and Mining

1. Introduction
Nowadays the amount of data is increasing very rapidly. In data mining, we deal with such huge amount of data which can be of any type and any volume. Earlier it was quite difficult to store and handle such bulky data. But these days’ remarkable strategies have enabled researchers to store huge amount of data and then process it. Stream data is the most important part of it. Stream data is a continuous process and is dynamic in nature. Its features keep on changing regularly. Such data usually come in a raw format and is of no use to researchers. Hence in order to utilize the data in an efficient manner we first need to convert it into some knowledgeable form. Only then we can process it and apply operations on it.
Data streams are difficult to process also because of the four main challenges posed by them. These are infinite-length, concept-evolution, concept-drift and feature-evolution. Since data stream is a fast and an ongoing process, it is assumed to be of infinite length. Hence, it becomes impractical to store such large volume of historical data for processing and training. Concept drift is said to be present when the underlying concept of the streams change with the time duration. Due to this the features of the classes show a drift towards the new features. Third one, concept-evolution occurs due to occurrence of new classes in the data stream. Altogether new classes that are unknown to our system or for which our system has not been trained start occurring in the stream. Our system will never be able to handle such classes. Final and the last one is the feature-evolution. This says that new features start appearing in the stream and the earlier features start to fade away and slowly after long period of time the feature set of the system changes to a great extent. Due to the above mentioned challenges and properties of the data streams, static data classification techniques cannot be used to handle stream data. Hence new efficient techniques have been proposed and are yet to be proposed to handle stream data. Like for handling infinite-length problem, researchers have proposed various incremental learning models. In order to handle the problem of concept-drift we need to identify the changes occurring in the concept of the steam. The model also needs to be regularly updated with these changes. Several models have been generated to handle this problem efficiently. Many of the models generated till now assume that the number of classes is fixed in a stream and they are not aware of the new classes occurring in the data. But in real time scenarios this is not the case. Altogether new classes occur frequently in the stream. So such models are not able to process the streams efficiently. Hence the need to train the classifier or the model with these new classes arises. As an example, in the intrusion detection mechanism, our model is trained with several different attacks. When the attacker tries to attack with a new strategy, our model cannot classify or detect it. So we need to update our model with this new type of attack. This problem has not been tackled by many researchers but some have proposed to handle it also. Traditional classifiers that work with labeled data will not be able to detect novel classes when they arrive until they are trained with the labeled instances of the novel class. Hence in order to detect novel classes the classifier model must be able to mechanically detect the novel classes before it is trained with the instances of novel class. For last challenge i.e. feature-evolution we make our model more efficient by keeping track of new features arriving in the data set. In this paper we make efforts to handle the problems using the string comparison operations. We use an ensemble of models. First we detect the outliers from each model and then we find the final outliers. Then we work to separate instances based upon the cause of their occurrence i.e. concept-evolution, concept- drift or noise. And then we update the model with the new features.
2. Related Work
Infinite-length and concept-drift have been effectively solved by researchers but much work has not been done to handle the other two problems. Researchers have proposed various incremental approaches. These approaches are of two types. Single model incremental approach (like in [1] ), here only one model is used for classification and the same model is updated dynamically and regularly with time. Second one is Hybrid-batch incremental approach (proposed in [2] [3] ). It uses an ensemble of models and the batch learning technique. Each model is generated from recent data using batch learning and the outdated and obsolete models are discarded on the basis of their efficiency. The advantage of using hybrid approach is that it is easy and simple to update the models. The occurrence of outliers (explained below) in a data stream is due to several reasons like noise, concept-evo- lution or concept-drift. Our main task is to distinguish among the cause for the occurrence of an outlier. Otherwise an instance belonging to an existing class, because of concept-drift, may be misclassified as an outlier. Hence, false alarm rate will be high (misclassifying an existing class instance as novel class instance).
Another technique is proposed by Spinosa et al. (in [4] ) that handles concept-evolution also along with concept-drift and infinite-length. Its approach uses a clustering technique to detect novel classes. It creates a model by applying clustering on normal data and this model is encompassed by a specified hyper-sphere. As the stream progresses, model is continuously updated. If a cluster formed lies outside the hyper-sphere and if its density is considerable then the cluster is declared as a novel class. But the problem with this approach is that it assumes only one class a normal and rest classes are novel. It behaves like a one class classifier. So this approach cannot be used with the data having multiple classes. It also makes an assumption that the shape of instances of normal class in the feature space is convex. But in real time situation this might not be the case.
Also many of the novel class detection strategies are of two main types: parametric and non-parametric. Parametric approaches assume some distribution of data and then it calculates the parameters of the distribution by using the normal data. And if any instance doesn’t follow the distribution parameters, it is declared as novel instance. Hence such strategies are restricted to the data distributions. Non-parametric techniques (in [5] - [7] ) never assume any data distribution and hence are not restricted. Our technique is also non-parametric. Also majority of the approaches developed for detecting the novel classes are able to detect the presence of only one novel class. If more than one novel class is present in the data, the models fail to identify two different novel classes. Our model is able to detect multiple novel classes present in the data and is a multi class classifier.
3. Proposed Approach
In our approach we generate a classifier that is an ensemble of three models. That is the number of models in the ensemble are three.
While dealing with data streams, we must first clear certain facts about it. First of all, these have two types of classes viz, an existing class and a novel class. Let’s assume that L is an ensemble of models consisting of models {M1, M2, ∙∙∙, Mn}.
Definition 1: Existing Class: If a model Mi that belongs to ensemble is trained by a class “C” and defines it, then class “C” is called an existing classes. In other words at least one model belonging to ensemble M must be trained on class C.
Definition 2: Novel Class: if there is a class “N” that is not known to any of the models Mi belonging to ensemble M, then “N” is a novel class. No model of the ensemble has been trained on novel class.
Definition 3: Outliers: if x is a test instance and if doesn’t match the specifications of any of the class “C” of the model Mi then “x” is an outlier of the model Mi. Outliers don’t belong to any of the class defined by the model.
3.1. Training Phase
In the training phase we first divide the data into equal sized chunks. The size of the chunks is set to be 2000. Each chunk contains different number of classes. We then apply K-medoid clustering technique on each chunk to obtain the different classes in the chunks. We used K-medoid clustering technique because it is performs well when the data contains outliers. Each chunk in the training phase generates a separate model. We store the summary of the classes or the clusters created. In it we store the number of clusters created and the set of words (Si) defining the cluster. Also the training is done on the recent data chunks. Classification is done by the ensemble as follows: If “X” is a test instance, it will first be sent to each model Mi in the ensemble to check whether if it is an outlier for that model. If it is not an outlier (OUT), it will be classified by model Mi that contains its class and if it is detected as an outlier by all the three models then it will be considered as a final outlier i.e. FOUT.
3.2. Outlier Detection
Once the three models have been generated and their summaries have been stored in the form of number of clusters and the set of words defining the clusters. We take a next step to detect outliers. When a test instance arises, it is sent to each model Mi for classification. We collect the words present in the test instance and check whether those words are present in the set of words “Sj” defining the any of the class “C” of the model. If say those words are present in the Sj of class “Cj” then it is classified as the instance belonging to the class “Cj” of model “Mi”. If the test instance does not belong to any of the class defined by the model “Mi”, it is declared as an outlier (OUT) for that model “Mi”.
Second step in outlier detection is to get the final outliers of the ensemble. In the above step, we store the outliers of each model “Mi” in a separate vector “OUTi”. To get the final outliers “FOU”, we see whether a particular instance in the “OUTi” is present in the other outlier arrays or not. If there are instances that are present in all the outlier arrays i.e. “OUTi”, then it is declared as final outlier “FOUT”. We store these final outliers in an array say “FOUTVECTOR”.
Algorithm 1. F_OUTVECTOR
Input: Models Mi and instances “X”.
Output: FOUTVECTOR (Vector containing outliers of the model).
1: For each model “Mi” in M
2: If 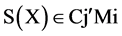 then
then
3: Append “Cj” to “X”.
4: else
5: Add “X” to OUTi.
6: End if.
7: End for.
8: FOUTVECTOR = Intersection (OUT1, OUT2, ∙∙∙, OUTi);
3.3. Handling Concept-Drift
3.3.1. Detecting Concept-Drift
Once FOUTVECTOR has been obtained, we must know that it contains three types of outliers. There are outliers due to concept-drift, outliers due to concept-evolution and outliers due to noise. Our next task is to separate these instances based on the cause of their occurrence. We first look for the concept-drift and try to handle it. For an instance OUTk from FOUTVECTOR, we obtain its set of words “Sk”, we now compare “Sk” with the word set of different clusters belonging to the model Mi and perform the set intersection operation on Sk and word set “Sj” of different classes “Cj”. We then check the result obtained against the word set “Sk” of instance. If more than 50% of the words in both the sets are same then we say that the outlier occurred due to concept-drift in the data. We then store such instances in the VECTOR named CONDRIFT.
3.3.2. Handling Concept-Drift
For handling Concept-Drift we obtain the cluster or the class to which the instance OUTk originally belongs to. Then we perform the set difference operation on word set “Sk” of each instance in CONDRIFT and the word set “Sk” of the class to which it belongs. The result contains the set of newly occurring words. We store the result of this set difference in the vector called DRIFTWORD along with the class information from which the instance drifted. And then all the new unique words are obtained. Then a matrix is constructed with all its initial values set to 1. Rows of the matrix denote the new unique words and the columns of the matrix denote the classes “Cj” of the model “Mi”. For each occurrence of new drift word “Wm” of class “Cj” we increment the value in the matrix at position CHKMAT [m, j] by 1. At the end we set the threshold value and if the count CHKMAT [m, k] is greater than the specified threshold, we then append the word ‘Wm’ to the word set “Sj” of class “Cj”. In this way the problem of concept-drift is handled.
Algorithm 2. CONCEPT_DRIFT
Input: FVECTOR and Model ‘Mi’
Output: CONDRIFT (Instances having concept-drift and updated Model)
1: For each OUTk in FOUTVECTOR
2: For each cluster Cj in model Mi
3: Result ← Set-Intersection (Sk, Sj)
4: If ((OUT(Cj)) and (S(Result) ≥ (50% of Cj))) then
5: CONDRIFT ← OUTk.
6: Store information about Cj in JCOUNT.
7: End if
8: End for.
9: End for.
10: For each instance “X” in CONDRIFT belonging to cluster Cj
11:DRIFTWORD←Set-Difference (Xi, Sj)
12: End for.
13: Unique_driftword ← Unique (DRIFTWORD).
14: For each “Wm” in Unique_driftword
15: For each Class Cj in Mi
16: CHKMAT[m,j] ← CHKMAT[m, j] + 1.
17: End for
18: End for
19: If (CHKMAT[m, j] > Threshold) then
20: Append word Wm to “Sj” of Class “Cj”
21: End if.
21: End algorithm.
3.4. Concept-Evolution
3.4.1. Detecting Concept-Evolution
Here we again consider the vector FOUTVECTOR. If the instance OUTk the vector does not meet the above set criteria of concept-drift, i.e. if it does not belong to any of the classes “Cj” of any of the models “Mi” then we say that it occurred due to concept-evolution and we store such instances in the vector CONEVO. The main criteria here required to be satisfied is that if more than 50% words of the instance and any of the class don’t match then it is due to concept-evolution.
3.4.2. Handling Concept-Evolution
While handling concept-evolution, we not only need to form a new class but we also need to differentiate between more than one novel classes occurring in the stream. We can obtain these different classes by applying the clustering algorithm on the CONEVO vector. It will provide us as many clusters as the number of classes in the CONEVO vector. After obtaining these classes we simply append these clusters to the models Mi of our ensemble. In this way our model now can detect new classes also.
Algorithm 3: CON_EVOLUTION.
Input: FVECTOR and Model “Mi”
Output: CONEVO (vector having instances due to concept_evolution)
1: For each OUTk in FOUTVECTOR.
2: For each cluster Cj in model Mi
3: Result ← Set Intersection (Sk, Sj)
4: If ((OUT(Cj)) and (S(Result) < (50% of Cj))) then
5: CONEVO ← OUTk.
6: End if
7: End for
8: End for
9: Apply K-medoid clustering on CONEVO.
10: Obtain new clusters.
11: Append these new clusters to any of the previous models Mi.
12: End algorithm.
4. Data Sets
The main requirement of our algorithm is that the data set used must not contain data that are multi-labeled. Each instance must belong to one class only.
4.1. 4 University Data Set
We first started working on the “4 university data set”. It contains the data from the four different universities. We applied preprocessing to the data set. After obtaining the final data we found that the dataset contained multi- valued and multi-labeled data that are unfit for our strategy. So we could not work on it.
4.2. NASA Aviation Safety Reporting System
NASA ASRS dataset contains the information about the various accidents that took place in the air industry. This data set is available online on NASA’s official website. Each instance represents an accident and the possible reasons and outcomes related to them. Each event has a related anomaly. Each one of the event anomalies is considered as a different class, like Aircraft problem: less severe, Aircraft problem: more critical, etc. The data also contains various multi-labeled and multi-valued attributes. It also contained rows and columns having incomplete information. We applied preprocessing to it and deleted all such rows and columns from the data set. The number of features and classes were reduced. It contained six normal classes and two novel classes. It contained both concept-drift and concept-evolution.
5. Result and Discussion
5.1. Techniques
SCND: This is the approach developed by us in this paper.
O-F Approach: OLINNDA-FAE approach is the combination of OLINNDA Approach discussed in [8] and FAE approach discussed in [9] . In this combined approach OLINNDA works as a novel class detector and FAE is used for classification. Mine-class is an existing approach developed by M. Masud et al. and is discussed in detail in [10] . MCM i.e. Multi Class Miner scheme is also an existing approach developed by M. Masud et al. in [11] .
5.2. Experiments
Number of models in the ensemble = 3
Number of instances in chunk = 2000
While handling all these problems we can say that in our strategy no instance belonging to novel class was declared as an existing class instances (discussed below with table). And very few instances belonging to existing class were declared as novel class instances. That is the false alarm rate will be negligible (Refer Table 1 and Table 3). The problem here was that there were instances, that belonged to existing class and that met our set criteria also remained unclassified due to some unknown reason. There were some instances that had drifted from the classes but because the count of the new features due to which they drifted was small and did not meet our criteria of threshold were also not classified by our model. So those new features could not be handled. Such features can be classified as noise (Refer Table 1). We are mentioning this here because the total count of those unhandled features was considerable in the complete dataset but it was not sufficient in individual chunk. They will be handled when their count will be considerable in individual chunk. This result is obtained due to the thresholding process that we used in our algorithm. This proves that the classification would have been better if the threshold is set to some lower value. It would have given more fine classification then. We can also get better classification if the chunk size is chosen smaller. Also our approach is not able to handle the feature-evolu- tion efficiently.
Table 1 shows the ERROR rate of the model. Here ERROR rate is defined as the percentage of outliers in the data that cannot be classified. Misclassification gives the percentage of the instances detected that could not be classified. False Alarm rate provides us the percentage of the instances that were wrongly classified (i.e. novel instances were detected as drifting instances and drifting instances were classified as novel instances).
Now we try to find out the timing requirements of our system. We also compare it with some other approaches. Here the time calculated is in seconds and is for one thousand instances of the dataset. In our approach the major portion of the time is utilized in loading the instances or data set i.e. about 20 seconds per thousand instances while the running time of the algorithm is about 13 seconds only. Lesser time is required for classification. We can see the results in Table 2.
We also compare the experimental results obtained with the previously developed approaches. Here ERROR is the total error rate of the classifier. Fnew here provides us the percentage of existing class instances defined as novel class instances. Mnew provides us the percentage of the novel class instances declared as existing class instances. Here we can see that in our approach no novel class instance is declared as an existing class instance.
In short, we can say that other existing approaches (in [12] ) had certain novel class instances that were classified as existing class instances but our approach did not classify any novel class instance as an existing class instance. This can be seen in Table 3 that Mnew entry is empty. Also, the running time our algorithm is lesser than the running time of other techniques as shown in Table 2.
6. Conclusion and Future Scope
In this paper we try to propose a strategy based on string or pattern matching to handle data streams. This strategy can handle infinite-length, concept-evolution and concept-drift. It is also able to detect multiple novel
Table 1. Summary of results.
Table 2. Running time (in seconds).
Table 3. Comparison of results.
classes occurring simultaneously. This strategy is different from all other strategies, as they use distances to handle these problems. But we used string matching to handle it. We didn’t work on distances. The false alarm rate in the strategy was quite low and was negligible. Also no novel class instance was classified as existing class instance. But this strategy is not able to handle feature-evolution effectively. Further work can be done to handle to feature-evolution effectively. Moreover this strategy considers the chunk size to be fixed. We could not handle dynamic size of chunk. Good research can be done to handle dynamic chunk size also.
Cite this paper
Rimjhim Singh,Manoj B. Chandak, (2015) Classification and Novel Class Detection in Data Streams Using Strings. Open Access Library Journal,02,1-8. doi: 10.4236/oalib.1101507
References
- 1. Aggarwal, C.C., Han, J., Wang, J. and Yu, P.S. (2006) A Framework for On-Demand Classification of Evolving Data Streams. IEEE Transactions on Knowledge and Data Engineering, 18, 577-589.
http://dx.doi.org/10.1109/TKDE.2006.69 - 2. Masud, M.M., Gao, J., Khan, L., Han, J. and Thuraisingham, B.M. Classification and Novel Class Detection in Data Streams with Active Mining.
- 3. Yang, Y., Wu, X. and Zhu, X. (2005) Combining Proactive and Reactive Predictions for Data Streams. In: Proceedings of the 11th ACM SIGKDD International Conference on Knowledge Discovery in Data Mining, ACM, New York 710-715.
- 4. Spinosa, E.J., de Leon F. de Carvalho, A.P. and Gama, J. (2008) Cluster-Based Novel Concept Detection in Data streams Applied to Intrusion Detection in Computer Networks. In: Proceedings of the 2008 ACM Symposium on Applied Computing, ACM, New York, 976-980.
- 5. Masud, M.M., Gao, J., Khan, L., Han, J. and Thuraisingham, B.M. (2009) Integrating Novel Class Detection with Classification for Concept-Drifting Data Streams. Proceedings of the European Conference on Machine Learning and Knowledge Discovery in Databases (ECML PKDD), 79-94.
- 6. Masud, M.M., Chen, Q., Gao, J., Khan, L., Han, J. and Thuraisingham, B.M. (2010) Classification and Novel Class Detection of DataStreams in a Dynamic Feature Space. Lecture Notes in Computer Science, 6322, 337-352.
http://dx.doi.org/10.1007/978-3-642-15883-4_22 - 7. Masud, M.M., Chen, Q., Khan, L., Aggarwal, C., Gao, J., Han, J. and Thuraisingham, B.M. (2010) Addressing Concept-Evolution in Concept-Drifting Data Streams. Proceedings of the IEEE International Conference on Data Mining (ICDM), 929-934.
- 8. Spinosa, E.J., de Leon F.de Carvalho, A.P. and Gama, J. (2007) OLINDDA: A Cluster Based Approach for Detecting Novelty and Concept-Drift in Data Stream. In: Proceedings of the 2007 ACM Symposium on Applied Computing, ACM, New York, 448-452.
- 9. Wenerstrom, B. and Giraud-Carrier, C. (2006) Temporal Data Mining in Dynamic Feature Spaces. Sixth International Conference on Data Mining (ICDM), Hong Kong, 18-22 December 2006, 1141-1145.
http://dx.doi.org/10.1109/ICDM.2006.157 - 10. Masud, M.M., Gao, J., Khan, L., Han, J. and Thuraisingham, B.M. (2011) Classification and Novel Class Detection in Concept-Drifting Data Streams under Time Constraints. IEEE Transactions on Knowledge and Data Engineering, 23, 859-874.
- 11. Masud, M.M., Gao, J., Khan, L., Han, J. and Thuraisingham, B.M. (2013) Classification and Novel Class Detection in Feature Based Stream Data. IEEE Transactions on Knowledge and Data Engineering, 25, No. 7.
- 12. Bopche, A., Nagle, M. and Gupta, H. (2014) A Review of Method of Stream Data Classification through Optimized Feature Evolution Process. International Journal of Engineering and Computer Science, 3, 3778-3783.


