Journal of Signal and Information Processing, 2011, 2, 178-183
doi:10.4236/jsip.2011.23024 Published Online August 2011 (http://www.SciRP.org/journal/jsip)
Cosine Modulated Non-Uniform Filter Banks
Jyotsna Ogale1, Samrat Ashok2
1Department of Electronics and Communication Engineering, Samrat Ashok Technological Institute, Vidisha, India; 2Department of
Electronics and Instrumentation Engineering, Samrat Ashok Technological Institute, Vidisha, India.
Received April 13th, 2011; revised May 19th, 2011; accepted May 29th, 2011.
ABSTRACT
Traditional designs for non-uniform filter bank (NUFB) are usually complex; involve complicated nonlinear optimiza-
tion with a large number of parameters and lack of linear phase (LP) property. In this paper, we describe a simple de-
sign method for multirate near perfect reconstruction (NPR) cosine modulated filter banks with non-uniform frequency
spacing and linear phase property that involves optimization of only single parameter. It is derived from the uniform
cosine modulated filter bank (CMFB) by merging some relevant band pass filters. The design procedure and the struc-
ture of the uniform CMFB are mostly preserved in the non-uniform implementation. Compared to other design methods
our method provides very good design and converges very rapidly but the method is applicable, only if the upper band
edge frequency of each non-uniform filter is an integral multiple of the bandwidth of the corresponding band. The de-
sign examples are presented to show the superiority of the proposed method over existing one.
Keywords: Cosine Modulation, Merging, Non-Uniform Filter Bank, Near Perfect Reconstruction
1. Introduction
Multirate filter bank find wide applications in many areas
of digital signal processing such as sub-band coding,
transmultiplexer, image, video and audio compression,
adaptive signal processing [1-3]. On the basis of time-
frequency resolution, filter bank can be classified in two
categories, i.e., uniform and non-uniform filter bank.
Uniform filter bank provides fixed and uniform time
frequency decomposition [1]. However in some applica-
tions like audio analysis and coding, broadband array
signal processing non-uniform and variable time-fre-
quency resolution may lead to better performance and
reduced arithmetic complexity, which is provided by
non-uniform filter bank [NUFB] [4-6]. Therefore effi-
cient structure and design procedures for NUFB are
highly desirable. Over the years, a number of design me-
thods have been proposed by different authors [6-10].
Among these, only few of them possess linear phase (LP)
property. The tree structure method [1] is an easy way to
design LP-NUFB via cascading uniform filter bank.
However, the limitation of decimation factors and the
long system delay are two major drawbacks of using this
method. Most of the available approaches [6-10] for
NUFBs, use standard constrained or unconstrained opti-
mization techniques to obtain the design, which tend to
be computationally expensive, when high order filters are
used. In wideband audio signal analysis and coding, filter
banks with high stop band attenuation greater than 100
dB is required. Moreover, it is difficult to design NUFBs
with high stop band attenuation and LP property. In [11],
a simple design method for NUFBs was proposed. It is
based on the design of a uniform cosine modulated filter
bank and is applicable only to non-uniform integer- de-
cimated filter banks. Moreover, it still involves compli-
cated nonlinear optimization with large number of pa-
rameters. Recently, Zing et al. [12] proposed interpolated
FIR prototype filter to design the NUFB.
In this work, a simple design approach for linear phase
NUFB is presented. The approach is based on uniform
CMFBs] as shown in Figure 1. The constituent NUFB as
shown in Figure 2 is obtained by merging some relevant
uniform filters in the associated uniform CMFB. The
design procedure is therefore reduced to the design of the
prototype filter in the associated uniform CMFB. With
this approach NUFBs with high stop band attenuation up
to 110 dB can be easily designed. A single variable opti-
mization is used to obtain minimum value of amplitude
(Emax) and aliasing (Ea) distortions [1].
2. Cosine Modulated Filter Bank
2.1. Uniform
Cosine modulation is a cost effective technique for M-

Cosine Modulated Non-Uniform Filter Banks179
-band filter bank [1]. In this approach all the filters of
analysis and synthesis section are obtained by cosine
modulation of single linear phase prototype low pass
filter which normally has linear phase and a finite length
impulse response as shown in Figure 1. Let H(z) be the
transfer function of the prototype filter. It is given as:
 
1
0
Nn
n
H
zhnz


 (1)
The impulse responses of filters of analysis and syn-
thesis sections are obtained from the closed form expres-
sions as given by [1]:
 
 
π
()2cos 21(1)
22
π
()2cos 21(1)
22
for 01, 01
k
k
k
k
N
hn hnkn
M
N
fn hnkn
M
kM nN



 





 


 
π
4
π
4






(2)
The required prototype filter is designed by window
technique using Kaiser Window function.
2.2. Non-uniform
In the case of non-uniform NPR filter banks, the concept
of cosine modulating low pass filters is applied [11,13].
After designing the required uniform CMFB, the corre-
sponding NUFB is obtained by merging the relevant
band pass filters of analysis and synthesis section of the
uniform filter bank as described below [13].
We define

i
H
z, 0,1, 2,,1iM, to be the filters
obtained by merging the adjacent analysis filters,
i.e.,

1
i
l

k
H
z’s, for i = ni through () in a uniform
M-channel CMFB. More specifically,
1
ii
ln
 
1
01
ii
i
nl
ik
kn
HzH zi M



 (3)
where ni+1 = ni + li .We define

i
F
z,
0,1, 2,,1iM in a similar manner for the synthesis
filters

k
F
z’s of the M-channel CMFB. That is,
 
1
1 01
ii
i
nl
ik
kn
i
FzF ziM
l



 (4)
x
(n)

0
H
z
M

M


0
F
z
M

M

M

M


1
H
z

1M
H
z

1
F
z

1M
F
z


ˆ
x
n
Figure 1. M-channel uniform filter bank.
Then


i
H
z and ()
i
F
z, 0,1,2,,1iM, form a
new set of analysis and synthesis filters in the
M
-
channel non-uniform CMFB. Note that 2
M
01
0nn n
nM

, and 012 1M llll M


 . Figure
2 shows the resulting overall structure of the
M
-chan-
nel non-uniform CMFB where

ii
lMM ,
0,1, 2,,1iM

, amounts to the decimation ratio for
the ith channel.
3. Optimization Technique
In NPR, perfect reconstruction condition is relaxed by
allowing small amount of distortion. Three types of dis-
tortions occur at the reconstructed output, i.e, amplitude
(Emax), phase and aliasing (Ea) [1]. The aliasing and
phase distortion can be eliminated by careful design of
the linear phase FIR filter. However, amplitude distortion
can not be eliminated completely but can be minimized
by applying optimization technique [14]. Initially; John-
ston [15] developed a nonlinear optimization technique.
Later on many prominent authors such as Creusere et al.
[16], Lin et al. [17], Jain et al. [18], have simplified it
using linear optimization technique with objective func-
tion as given below:
 
22
(/)
max 1
for 0π
jjM
aHe He
M







(5)
In this work same objective function in modified form
is used for the design of non-uniform filter bank, as given
below vaidynathan [1]:

12
0
1
max 1
for π
Mj
i
i
He
MM









 (6)
where,
M
is number of channels in non-uniform filter
bank and


j
i
H
e

is the frequency responses of the
filters of the non-uniform section. Initially, input pa-
rameters, i.e., sampling rate, number of band, pass band
and stop band frequencies, pass band ripple and stop
nd attenuation of prototype filter are specified. Cutoff ba
x
(n)

0
H
z

0
M

0
M



0
F
z
1
M

1M
M


1
M

1M
M



1
H
z


1M
H
z




1
F
z


1M
F
z



ˆ
x
n
Figure 2. -channel nonuniform filte r bank.

M

Cosine Modulated Non-Uniform Filter Banks 180
freque itioeter- ncy, transn band and filter length is than d
mined. Initialize, different optimization pointers like step
size, search direction, flag and initial (perror) as well as
expected minimum possible values (terror) of the objec-
tive function. Inside the optimization loop, design the
prototype low pass filter and determine the band pass
filters for analysis and synthesis sections using cosine
modulation. Obtain the desired NUFB using merging of
relevant band pas filters. In optimization routine cutoff
frequency of the prototype filter is gradually changed as
per the search direction and calculates the corresponding
value of the objective function. Algorithm halts when it
attains the minimum value of the objective function. The
flowchart of optimization Figure 3 is given below and
Specify stop band attenuation
(A
s
), number of bands (M)
Initialize: passband (ω
p
)
,
stopband freq (ω
s
),
terror, perror, step, dir, and flag
Calculate cutoff frequency (ω
c
). Filter order (N) and
design the prototype filter. Obtained filters of
analysis section using cosine modulation. Obtain
NUFB using merging filters.
obtain absolute value of objective function. φ
׀perror׀ =׀φ׀
(ω
c
= ω
c
+ dir.step) and determine φ at
new cutoff frequency.
Step = step/2
dir = -dir
Yes
No
Yes
No
Is ׀φ׀ ≤ terror׀
or
׀perror׀ =׀φ׀
Is ׀φ׀ ≤ terror׀
or
׀perror׀ =׀φ׀
Stop
Figure 3. Flow chart of optimization algorithm.
simul
d 5-channel NUFBs are de-
n
fa
ated on MATLAB 7.0.
4. Design Examples
In this section 3-channel an
signed and the performance of proposed technique is
compared with the earlier reported work [5,11,12,19].
In this example a 3-channel NUFB with decimatio
ctor (4, 4, 2) has been designed using same specifica-
tions as given in Xie et al. [5] and Li et al. [11]. The de-
sign specifications of the filter are: stop band attenuation
100
s
A

dB, N = 63, 01l

, 11l, 22l and 00n

,
11n

, 22n

. Thndeuencie e ba edg freqs are
14


,22



NUFB,
. The magnitude responses of proto-
optimized value of amplitude distor-
tion is shown in Figures 4-6. The obtained value of
maximum amplitude distortion is Emax = 2.99 × 10–3.
This example is quoted to compare the performa
type filter,
nce
with recent work of Zing et al. [12]. In the work of [12],
5-channel NUFB with integer decimation factors (4, 4, 8,
8, 4) is designed using IFIR based prototype filter. The
reported length of model and interpolator filters are Nm =
00.1 0.2 0.3 0.4 0.50.5
-200
-160
-120
-80
-40
00
Norm alized fr e quency
Magnit ude (dB)
Figure 4. Magnitude response of optimized prototype filter.
00.1 0.2 0.3 0.4 0.50.5
-15 0
-12 0
-90
-60
-30
00
Normalized f r eq uency
M agnitude (dB)
Figure 5. Magnitude response of three- channel filter bank.

Co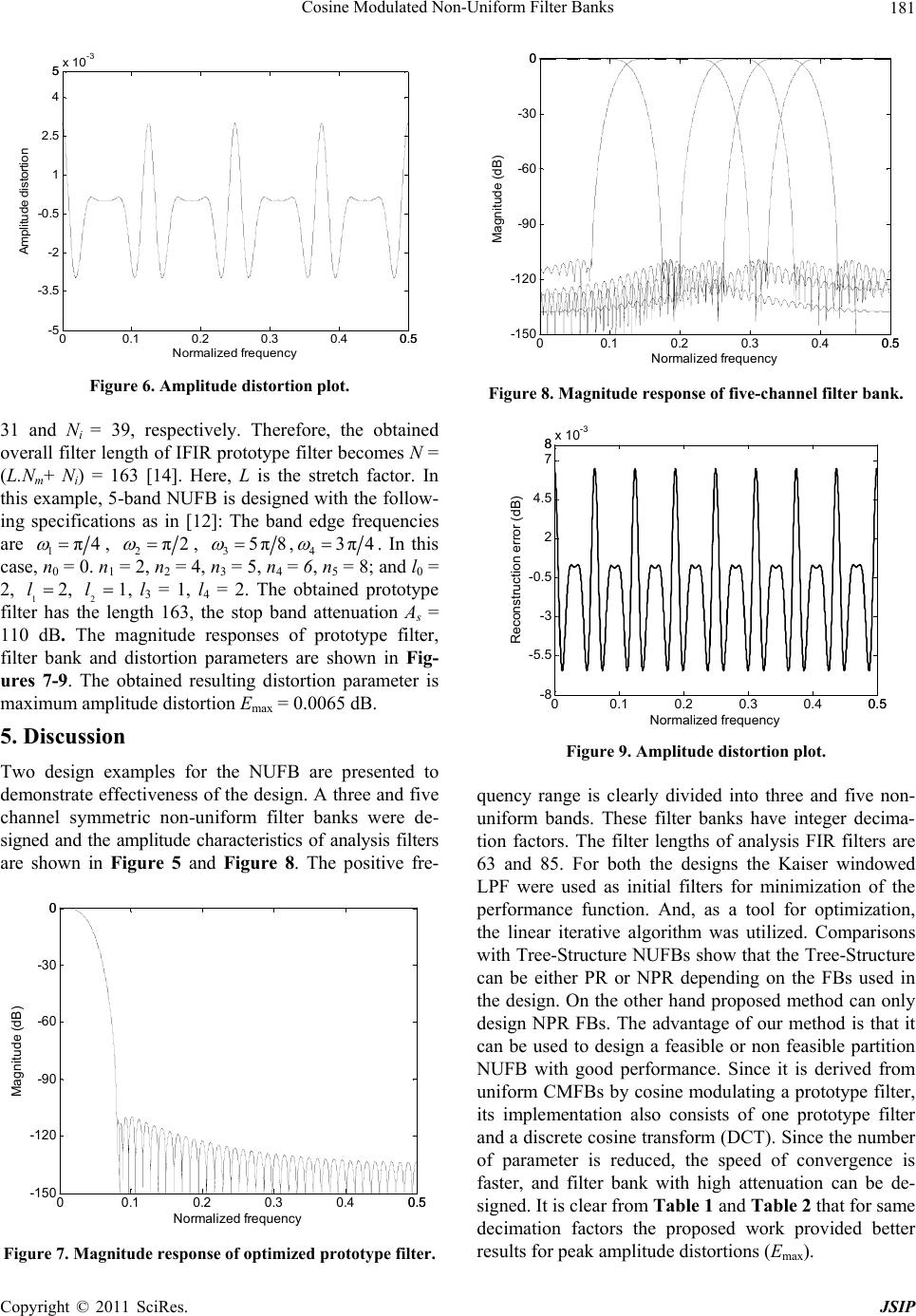sine Modulated Non-Uniform Filter Banks181
00.1 0.2 0.3 0.4 0.50.5
-5
-3.5
-2
-0.5
1
2.5
4
55 x 10-3
Norm a lized fr eq uen cy
Amp litude distort ion
Figure 6. Amplitude distortion plot.
1 and N= 39, respectively. Therefore, the obtained 3i
overall filter length of IFIR prototype filter becomes N =
(L.Nm+ Ni) = 163 [14]. Here, L is the stretch factor. In
this example, 5-band NUFB is designed with the follow-
ing specifications as in [12]: The band edge frequencies
are 1π4

, 2π2

, 35π8


,43π4

. In this
case 0n1 = 2, 234=5 and l0 =
2, 1
l2, 2 l1, l3 = 1, l4 = 2. The obtained prototype
filts tngth 163, the stop band attenuation As =
110 dB. The magnitude responses of prototype filter,
filter bank and distortion parameters are shown in Fig-
ures 7-9. The obtained resulting distortion parameter is
maximum amplitude distortion Emax = 0.0065 dB.
, n = 0. n = 4, n = 5, n 6, n = 8;
ples for the NUFB are presented to
er hahe le
5. Discussion
Two design exam
demonstrate effectiveness of the design. A three and five
channel symmetric non-uniform filter banks were de-
signed and the amplitude characteristics of analysis filters
are shown in Figure 5 and Figure 8. The positive fre-
00.1 0.20.3 0.4 0.50.5
-150
-120
-90
-60
-30
00
Normalized fr e quen cy
Magnitude (dB)
00.1 0.2 0.3 0.40.50.5
-150
-120
-90
-60
-30
00
Norma lized fr equency
M agnitu de ( dB)
Figure 8. Magnitude response of five-channel filter bank.
00.1 0.2 0.3 0.4 0.50.5
-8
-5.5
-3
-0.5
2
4.5
7
88x 10
-3
Normalized frequency
Reconstruction er ror (dB)
Figure 9. Amplitude distortion plot.
quncy range is clearly divided into three and five non- e
uniform bands. These filter banks have integer decima-
tion factors. The filter lengths of analysis FIR filters are
63 and 85. For both the designs the Kaiser windowed
LPF were used as initial filters for minimization of the
performance function. And, as a tool for optimization,
the linear iterative algorithm was utilized. Comparisons
with Tree-Structure NUFBs show that the Tree-Structure
can be either PR or NPR depending on the FBs used in
the design. On the other hand proposed method can only
design NPR FBs. The advantage of our method is that it
can be used to design a feasible or non feasible partition
NUFB with good performance. Since it is derived from
uniform CMFBs by cosine modulating a prototype filter,
its implementation also consists of one prototype filter
and a discrete cosine transform (DCT). Since the number
of parameter is reduced, the speed of convergence is
faster, and filter bank with high attenuation can be de-
signed. It is clear from Table 1 and Table 2 that for same
decimation factors the proposed work provided better
results for peak amplitude distortions (Emax).
Figure 7. Magnitude response of optimized prototype filter.

Co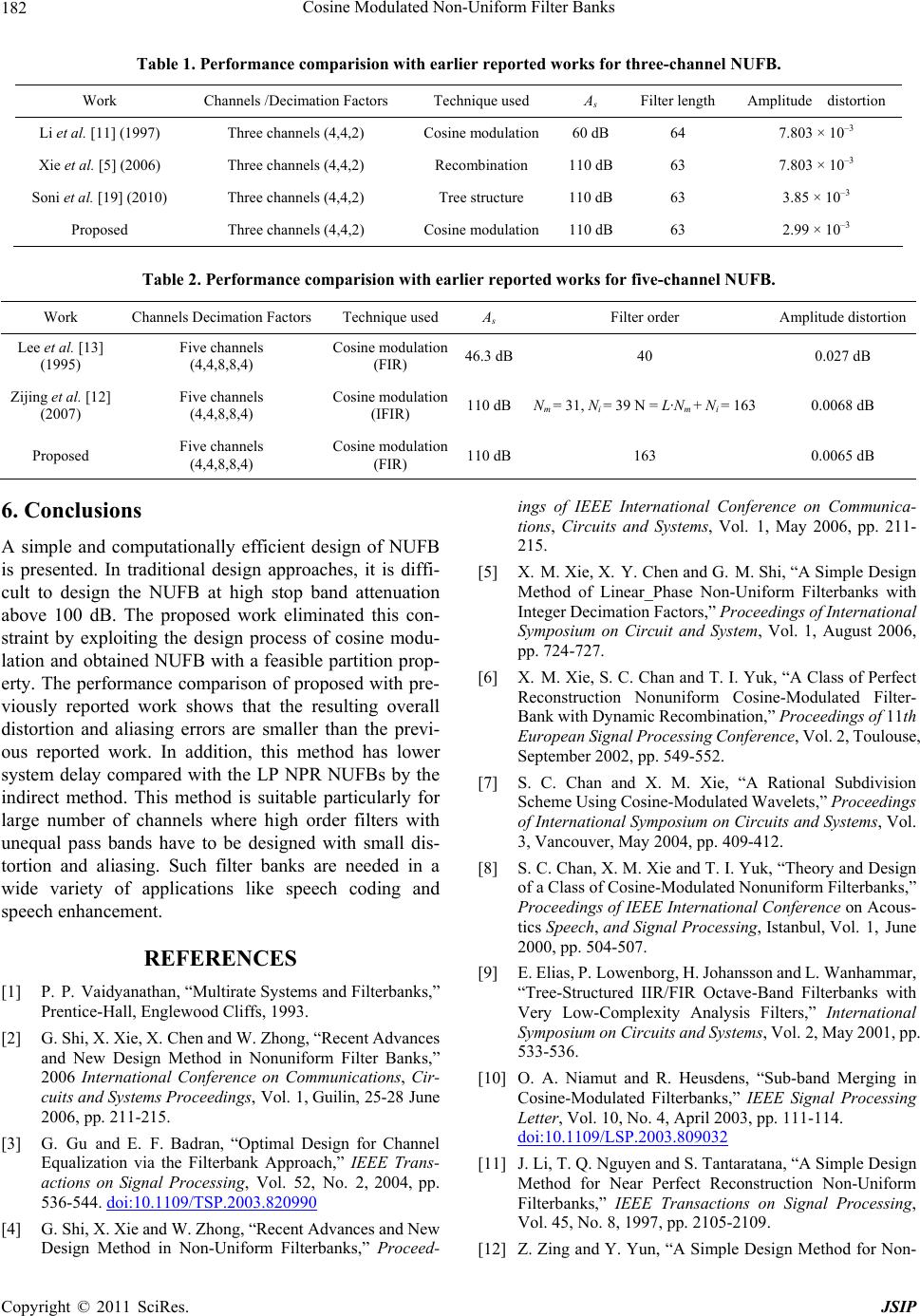sine Modulated Non-Uniform Filter Banks 182
ision with earlier reported works for three-channel NUFB.
Work Channels /Decimation Factors Technique used As Filter length Amplitude distortion
Table 1. Performance compar
Li et a1997) Cosine 60 dB l. [11] (Three channels (4,4,2) modulation 64 7.803 × 10–3
Xie et al. [5] (2006) Three channels (4,4,2) Recombination 110 dB63 7.803 × 10–3
S
Cn
oni et al. [19] (2010) Three channels (4,4,2) Tree structure 110 dB63 3.85 × 10–3
Proposed Three channels (4,4,2) osine modulatio110 dB63 2.99 × 10–3
Table 2. Performance comparision with earlier reported works for five-channel NUFB.
Work Channels DecimsAmplitude distortionation Factors Technique used A Filter order
Lee 3] C46.3 dB40 0.027 dB et al. [1
(1995)
Five channels
(4,4,8,8,4)
osine modulation
(FIR)
Zijin Five channels Cosination 110 dBNm = 31, Ni = 39 N = L·Nm + Ni = 163 0.0068 dB
Proposed Five channels Cosine m110 dB163 0.0065 dB
g et al. [12]
(2007) (4,4,8,8,4)
e modul
(IFIR)
(4,4,8,8,4)
odulation
(FIR)
. Conclusions
ationally efficient design of NUFB
REFERENCES
[1] P. P. Vaidyans and Filterbanks,”
Recent Advances
dran, “Optimal Design for Channel
6
A simple and comput
is presented. In traditional design approaches, it is diffi-
cult to design the NUFB at high stop band attenuation
above 100 dB. The proposed work eliminated this con-
straint by exploiting the design process of cosine modu-
lation and obtained NUFB with a feasible partition prop-
erty. The performance comparison of proposed with pre-
viously reported work shows that the resulting overall
distortion and aliasing errors are smaller than the previ-
ous reported work. In addition, this method has lower
system delay compared with the LP NPR NUFBs by the
indirect method. This method is suitable particularly for
large number of channels where high order filters with
unequal pass bands have to be designed with small dis-
tortion and aliasing. Such filter banks are needed in a
wide variety of applications like speech coding and
speech enhancement.
athan, “Multirate System
Prentice-Hall, Englewood Cliffs, 1993.
[2] G. Shi, X. Xie, X. Chen and W. Zhong, “
and New Design Method in Nonuniform Filter Banks,”
2006 International Conference on Communications, Cir-
cuits and Systems Proceedings, Vol. 1, Guilin, 25-28 June
2006, pp. 211-215.
[3] G. Gu and E. F. Ba
Equalization via the Filterbank Approach,” IEEE Trans-
actions on Signal Processing, Vol. 52, No. 2, 2004, pp.
536-544. doi:10.1109/TSP.2003.820990
[4] G. Shi, X. Xie and W. Zhong, “Recent Advances and New
ings of IEEE International Conference on Communica-
d of Linear_Phase Non-Uniform Filterbanks with
Nonuniform Cosine-Modulated Filter-
ed Wavelets,” Proceedings
orm Filterbanks,”
/FIR Octave-Band Filterbanks with
dulated Filterbanks,” IEEE Signal Processing
Design Method in Non-Uniform Filterbanks,” Proceed-
tions, Circuits and Systems, Vol. 1, May 2006, pp. 211-
215.
[5] X. M. Xie, X. Y. Chen and G. M. Shi, “A Simple Design
Metho
Integer Decimation Factors,” Proceedings of International
Symposium on Circuit and System, Vol. 1, August 2006,
pp. 724-727.
[6] X. M. Xie, S. C. Chan and T. I. Yuk, “A Class of Perfect
Reconstruction
Bank with Dynamic Recombination,” Proceedings of 11th
European Signal Processing Conference, Vol. 2, Toulouse,
September 2002, pp. 549-552.
[7] S. C. Chan and X. M. Xie, “A Rational Subdivision
Scheme Using Cosine-Modulat
of International Symposium on Circuits and Systems, Vol.
3, Vancouver, May 2004, pp. 409-412.
[8] S. C. Chan, X. M. Xie and T. I. Yuk, “Theory and Design
of a Class of Cosine-Modulated Nonunif
Proceedings of IEEE International Conference on Acous-
tics Speech, and Signal Processing, Istanbul, Vol. 1, June
2000, pp. 504-507.
[9] E. Elias, P. Lowenborg, H. Johansson and L. Wanhammar,
“Tree-Structured IIR
Very Low-Complexity Analysis Filters,” International
Symposium on Circuits and Systems, Vol. 2, May 2001, pp.
533-536.
[10] O. A. Niamut and R. Heusdens, “Sub-band Merging in
Cosine-Mo
Letter, Vol. 10, No. 4, April 2003, pp. 111-114.
doi:10.1109/LSP.2003.809032
[11] J. Li, T. Q. Nguyen and S. Tantaratana, “A Simple
Method for Near Perfect Rec
Design
onstruction Non-Uniform
Filterbanks,” IEEE Transactions on Signal Processing,
Vol. 45, No. 8, 1997, pp. 2105-2109.
[12] Z. Zing and Y. Yun, “A Simple Design Method for Non-

Cosine Modulated Non-Uniform Filter Banks183
International
ns on C
ew Delhi, 2001.
rbanks,” Proceedings of IEEE In-
ers for M-Band
Uniform Cosine Modulated Filterbank,”
Symposium on Microwave, Antenna, Propagation and
EMC Technologies, 2007, pp. 1052-1055,
[13] J. Lee and B. G. Lee, “A Design of Nonuniform Cosine
Modulated Filterbanks,” IEEE Transactioircuits
and System-II, Vol. 42, No. 1, November 1995, pp. 732-
737.
[14] S. K. Mitra, “Digital Signal Processing,” Tata Mc-Graw
Hill, N
[15] J. D. Johnston, “A Filter Family Designed for Use in
Quadrature Mirror Filte
ternational Conference on Acoustics, Speech and Signal
Processing, Denver, 1980, pp. 291-294.
[16] C. D. Cresure and S. K. Mitra, “A Simple Method for
Designing High-Quality Prototype Filt
Pseudo QMF Banks,” Transactions on Signal Processing,
Vol. 43, No. 4, 1995, pp. 1005-1007.
doi:10.1109/78.376856
[17] Y. P. Lin and P. P. Vaidyanathan, “
Approach for the Desi
A Kaiser Window
gn of Prototype Filters of Co-
sine-Modulated Filterbanks,” IEEE Signal Processing
Letter, Vol. 5, No. 6, 1998, pp. 132-134.
doi:10.1109/97.681427
[18] A. Jain, R. Saxena and S. C. Saxena, “An
Simplified Design of C
Improved and
osine Modulated Pseudo QMF
Filterbanks,” Digital Signal Processing, Vol. 16, No. 3,
2006, pp. 225-232. doi:10.1016/j.dsp.2005.11.001
[19] R. K. Soni and A. Jain, “An Optimized Design of Non-
Uniform Filterbank Using Blackman Window Family,”
International Journal of Signal and Image Processing, Vol.
1, No. 1, 2010, pp. 18-23.