Journal of Signal and Information Processing, 2011, 2, 218-226
doi:10.4236/jsip.2011.23030 Published Online August 2011 (http://www.SciRP.org/journal/jsip)
A Dual Tree Complex Discrete Cosine Harmonic
Wavelet Transform (ADCHWT) and Its
Application to Signal/Image Denoising
M. Shivamurti, S. V. Narasimhan
Digital Signal Processing and Systems Group Aerospace Electronic and Systems Division, National Aerospace Laboratories,
Bangalore, India.
Received March 23rd, 2011; revised April 30th, 2011; accepted May 11th, 2011.
ABSTRACT
A new simple and efficient dual tree analytic wa velet transform ba sed on Discrete Cosine Harmonic Wa velet Tran sform
DCHWT (ADCHWT) has been proposed and is applied for signal and image denoising. The analytic DCHWT has been
realized by applying DCHWT to the original signal and its Hilbert transform. The shift invariance and the envelope
extraction properties of the ADCHWT have been found to be very effective in denoising speech and image signals,
compared to that of DCHWT.
Keywords: Analytic Discrete Cosine Harmonic Wavelet Transform, Analytic Wavelet Transform, Dual Tree Complex
Wavelet Transform, DCT, Shift Invariant Wavelet Transform, Wavelet Transform Denoising
1. Introduction
The wavelet transform (WT) provides signal compres-
sion, denoising and many more desirable processing fea-
tures. In spite of these advantages, the WT suffers from
many major problems. The WT coefficients oscillate
about the zero value around the singularities. This will
reduce the magnitude of WT coefficients near singularity
where their values are expected to be large, making the
singularity extraction and signal modeling difficult. Fur-
ther, the WT is shift variant, i.e., around singularities,
even for a small shift in input signal, there will be a large
variation in the energy distribution among WT coeffi-
cients at different scales resulting in different WT pat-
terns which have to be considered for further processing
[1]. This is due to aliasing caused by decimation at each
wavelet level. Such a shift variant nature of WT not only
affects detection of transients but also denoising as signal
is reconstructed by decimated modified samples resulting
in strong glitches [2]. Also at low signal to noise ratio
like below 0dB, the conventional denoising fails. How-
ever the signal compression achieved by WT is not af-
fected by its shift variant property.
The WT is realized by a perfect reconstruction filter
bank which involves analysis filter bank, down sampling,
interpolation and synthesis filter bank. Here the aliasing
caused by the use of non-ideal filters is cancelled by the
synthesis filter bank. However the reconstructed signal
by such a filter bank is highly sensitive to coefficient
errors and may get affected severely. Further such a WT
suffers from poor directional selectivity for diagonal
features. The WT filters being real, separable and their
frequency response symmetric about zero in four quad-
rants in the 2D frequency space, cannot distinguish be-
tween two opposing diagonal directions, i.e. and
edge orientations [3,4].
o
45
o
45
The undecimated WT solves the shift variance with
additional computational load. However the directional-
ity problem remains unsolved as undecimated WT cannot
distinguish the two opposing diagonals as it uses separa-
ble filters. This blindness to such a directionality makes
the processing and modeling of image features like
ridges and edges difficult. For separable filters to have
proper directionality, their frequency responses should be
asymmetric for positive and negative frequencies and can
be achieved by using complex wavelet filters [4]. How-
ever the difficulty involved in the design of complex fil-
ters satisfying perfect reconstruction prohibits their use in
image processing.
The sinusoids in the Fourier transform in higher di-
mensions provide highly directional plane waves. The FT

A Dual Tree Complex Discrete Cosine Harmonic Wavelet Transform (ADCHWT) and 219
Its Application to Signal/Image Denoising
magnitude does not oscillate and provides a smooth en-
velope. Further the FT magnitude is shift invariant and
also it does not suffer from aliasing and the signal recon-
struction (inverse FT) does not involve any critical re-
construction criterion. These benefits are due to its com-
plex exponential basis instead of real basis of WT. Thus
realization of complex/analytic WT has become impor-
tant. This approach has been applied to image segmen-
tation, classification, deconvolution, image sharpening,
motion estimation, coding, water marking [4,5], texture
analysis and synthesis, seismic imaging and extraction of
evoked potentials in EEG [6]. The analytic WT (AWT)
has the features of both WT and FT and is appropriate for
time-frequency analysis like STFT [7].
The complex/analytic WT been realized using dual
tree filter bank structure and Hilbert transform (HT).
Many variations of this structure have been achieved
with various degrees of advantages and limitations. The
absence of negative frequencies for an analytic signal not
only reduces aliasing but also accounts for the decima-
tion by a factor of 2 at each DWT stage resulting in shift
invariance. But the global nature of HT (infinite both
time and frequency extent) converts the finite support
wavelet function to that of an infinite support and this
makes the shift invariance and alias free nature as ap-
proximate. The WT realized by a two channel perfect
reconstruction filter bank is computationally expensive
and complicated due to explicit decimation, interpolation,
associated filtering and involved delay compensation in
reconstruction.
The harmonic wavelet transform (HWT) proposed by
Newland [8] is simple and does not require explicit
decimation, interpolation and associated filtering. The
decimated components are achieved in the frequency
domain by taking the inverse transform of each group of
FT coefficients. The signal reconstruction is achieved by
the inverse FT of properly concatenated FT coefficient
groups. Here also, the WT coefficients become complex
due to lack of DFT real symmetry. Further, the DFT val-
ues will be generally affected by the leakage due to sig-
nal truncation resulting in poor quality signal decomposi-
tion. To overcome these, the DCT based harmonic
wavelet transform (DCHWT) has been proposed [9,10].
The real nature and the symmetrical signal extension of
DCT respectively result in a real and more exact WT
coefficients as the leakage is very much reduced [11].
The DCHWT has been used for signal/image compres-
sion and spectral estimation both with computational and
performance advantage. For speech and image signals,
the compression provided an adaptive wavelet packet
algorithm based on DCHWT has been found to be not
only better than that by DCHWT but also that by adap-
tive Daubechies-2 wavelet packet. Further it has been
used for efficient and accurate signal decomposition to
overcome the cross-terms in Wigner-Ville time fre-
quency distribution Also the DCTHWT has been extended
to realize its shift invariant version. [12] which reduces
the glitches when applied for denoising.
In the present work, a new dual tree analytic wavelet
transform based on DCHWT (ADCHWT) has been pro-
posed and is applied for signal and image denoising. The
analytic DCHWT has been realized by applying DC-
HWT to the original signal and its HT. The shift invari-
ance property of the ADCHWT has been illustrated and
its contribution in association with its envelope extrac-
tion property has been found to be very effective in de-
noising compared to that of DCHWT [13].
2. Dual Tree Analytic Discrete Cosine
Harmonic Wavelet Transform (ADCHWT)
In this section, the discrete cosine harmonic wavelet tran-
sform and the development of the new dual tree analytic
discrete cosine harmonic wavelet transform (ADCHWT)
will be considered.
2.1. Discrete Cosine Harmonic Wavelet
Transform (DCHWT)
The filter bank realization of WT, involves down sam-
pling of the components obtained by the individual ban-
dpass filters. The restoration of the processed signal cor-
responding to overall spectrum at the original sampling
rate, involves summation of the components after their
upsampling and image rejection filtering. The harmonic
wavelet transform based on DFT (DFHWT) realizes the
subband decomposition in the frequency domain by
grouping the Fourier transform (FT) coefficients and the
inverse of these groups results in decimated signals. Fur-
ther after processing, the FT of the subband signals can
be repositioned in their corresponding positions to re-
cover the overall spectrum, with the original sampling
rate. Therefore, this will not involve explicit decimation
and interpolation operations. As a consequence, no band
limiting and image rejection filters are necessary. Also,
while reconstruction, there are no delay compensations
as the subband groups are synthesized in frequency do-
main by repositioning them. In view of this, the harmonic
subband decomposition is very attractive due to its sim-
plicity. However in the DFHWT, the grouping of the
DFT coefficients with lack of conjugate symmetry makes
the WT coefficients complex. For reconstruction after
concatenation of the groups, the conjugate symmetry is
restored to get the real signal.
The DFHWT is very attractive as long as no process-
ing of the components is involved prior to inverse trans-

A Dual Tree Complex Discrete Cosine Harmonic Wavelet Transform (ADCHWT) and 220
Its Application to Signal/Image Denoising

formation. However, for a signal segment obtained with-
out using any window function, there can be a severe
leakage effect from one subband of the signal into an-
other. If different subbands have to be processed differ-
ently, this is not achieved as the signal energy from one
to another has already leaked. The DFHWT may be tol-
erable for a signal with well-separated frequency com-
ponents of sufficiently high magnitude. But for closely
spaced components of significantly different magnitudes,
during the computation of the FT itself, the energy will
leak from the higher amplitude component to the lower
one (and vice versa). This results in a large bias in the
spectral magnitude and may even totally eclipse smaller
amplitude spectral peaks. In such a case, decomposing
the signal based on DFHWT and processing the sub-
bands may not be very effective. Further leakage in
DFHWT will also limit its use in signal or image com-
pression application. The reason for this is that it is not
possible to get a good signal reconstruction by omitting
the lower scales (corresponding to high frequencies) in
WT as the leaked energy cannot be recovered unless all
the scales are considered. Therefore to utilize the attrac-
tive features of the harmonic wavelet transform, DCT is
used instead of DFT, which has a comparatively reduced
leakage effect. This is due to symmetrical data extension
which results in a smooth transition from one DCT pe-
riod to the other without any discontinuity.
The wavelet transform characterizes the
correlation or similarity between the signal

,
x
Wab


x
t

to be
analyzed and the wavelet function


tba

 . Such a
correlation is given by
 
*
12
1
,d
xtb
Wab xtt
aa







 (1)
where is the prototype/mother wavelet. By shift-
ing and scaling

t 


t  by the parameters and ,
respectively; all the basis functions
ba
  
tb

12
ta a 


,ab are obtained. Equation (1)
can be realized in the frequency domain using Parseval’s
theorem as
  
12
*
,
2π
jb
xa
WabXa e

d







(2a)
Therefore the, the wavelet transform can be derived by
windowing the spectrum


X

with

*a


 and
inverse Fourier transforming the product.



12 1*
,
x
Wab aFXa




 
(2b)


 and

X

are the FT of the mother wavelet
and the signal

t 

x
t. That is, for a
particular scale ‘a’ can be computed by the Equation (4b)
using

,
x
Wab



X

and


a

 by FFT algorithm.
For a real symmetric signal

S
x
t and a real sym-
metric wavelet


t
S
 function, Equation (2a) becomes
[9]
 
xs
X
 
12
,cosd
2πs
aa bCab

 


 (3a)
(x)
S

and


S

 are the Fourier transform of


S
x
t
and


St
 respectively. (Generally the wavelet func-
tion is a symmetrical one but to have consistency in the
notation


S is used). In other words, they are the
cosine transforms of
t 


S
x
t and the mother wavelet


St
 .


,b
x is the wavelet transform in cosine
domain instead of Fourier domain. Hence the corre-
sponding equation for Equation (2b) is
Ca

 
12 1
,
xs
b aC XaCas







 (3b)
Therefore the cosine wavelet transform coefficient


,b
x for a particular scale “a” can be computed by
the Equation (3b) using
Ca

s
X

and

sa


 by a fast
cosine transform algorithm which indirectly uses FFT
algorithm.


s



is very simple for the Harmonic
cosine wavelet transform (CHWT), and it is zero at all
frequencies except constant over a small frequency band.
00
00
1, ,
,
0,
cc
s
cc
otherwise


 







(3c)
For this the wavelet


St
 is,

0
sin cos
π
cc
Sc
t
tt
t





Representing sin c
c
t
t


by

sin c ct

,
 
0
cos sin
π
c
Sc
ttc


t

  (3d)
Hence the mother wavelet is a cosine modulated sinc
function. Here the decomposition of the signal in the
frequency domain is simple but suffers from the problem
of poor time localization due to slow decaying of the sinc
function. Though a spectral weighing other than rectan-
gular improves the localization in time it results in a
non-orthogonal wavelet set. The type of spectral weigh-
ing will determine the wavelet as it is the cosine trans-
form of the wavelet.
For the cosine harmonic wavelet transform, the spec-
tral weighing is a symmetrical rectangular function and
for a discrete signal it is zero except over symmetrical

A Dual Tree Complex Discrete Cosine Harmonic Wavelet Transform (ADCHWT) and 221
Its Application to Signal/Image Denoising
finite bands


π,πpq and


π,πpqwhere
can be real numbers, not necessarily integers.
,pq
For an orthogonal CHWT, the wavelet function is
fixed and corresponds to a rectangular weighing in the
frequency domain which results in such a wavelet trans-
form.
The Discrete cosine transform (DCT) enables the im-
plementation of the above cosine transform discussed as
it forms the symmetric signals

S
x
t and


St
 by
itself (for the given non-symmetric

x
t and


t  ).
For a sampled signal

x
n, , the
DCT of points, is defined as the DFT of a
point symmetrically extended signal

1nN0,1, 2

, ,

N2N
y
n.
 

,0
21, 21
xnn N
yn xNnNn N
  

 


1

y
n is even symmetric with respect to the

12N 
 
point . This leads to DCT and is given by
  

1
0
π21
2cos, 01
2
2, 21
N
n
x
x
kn
xnk N
Ck N
CNk NkN


  


 



(4)
Using the above

S


N
in the CHWT, the subband
decomposition is done in frequency domain unlike in
time domain by a filter bank. This is achieved by group-
ing the coefficients of a discrete cosine transform
(DCT) of length and this is equivalent to applying
a window or weighing by a constant in the frequency
domain.
2N
2
The DCT coefficients can be grouped in a way similar
to that of DFT coefficients and the DCT being real, there
is no necessity to do the conjugate operation in placing
the coefficients symmetrically [9]. The symmetrical
placement is also not necessary due to the very definition
of the DCT as it provides only half the number of coeffi-
cients and the inverse DCT definition takes care of the
symmetry. The grouped coefficients for each band have
to be treated as if they are the DCT coefficients of that
subband.
In the Figure 1 DCTHWT for a DCT size of 16 is il-
lustrated and the only one side of the symmetrical coeffi-
cient sequence is shown, i.e. (0 - 7). The last half part of
the coefficients correspond to scale-
. The lower half of the coefficients
xx
are split into two groups and the upper
group correspond to scale-1, .
 
4to 7
xx
CC

3

3
xx
CC



0,
x
CC 
0
0,. .,ie C

0Ct

oC

2,
1
Further the group x

is split into two
groups 2 and3 each having single coefficients
and x
C, respectively. The inverse DCT of
each of the groups ; result in WT coeffi-
cients of the scales , respectively. For
. .,ie C


1
0123
,, ,CCCC
0,1, 2,3
C C

0

1
x
C
32Q

,
Decomposition of input to scales
)1(
x
C)2(
x
C)3(
x
C
)0(
x
C)4(
x
C)5(
x
C)6(
x
C)7(
x
C
)1(
x
C)0(
x
C
)1(
x
C )0(
x
C)2(
x
C)3(
x
C
C 0
C
1
C
3
C
2
IDCTIDCT
IDCT
IDCT
)1(
x
C)2(
x
C)3(
x
C)4(
x
C)5(
x
C)6(
x
C)7(
x
C)0(
x
C
Discrete Cosine Transform

3
cn

2
cn


0
cn
DCT


1
cn
DCT DCT DCT
3
C2 C1 C0 C
IDCT


x
n
For a 16 point DCT
WT scales: c
3(n)
, c
2(n)
, c
1(n)
, c
0(n)
Reconstruction of in
p
ut from scales


3
cn


2
cn


1
cn


0
cn


x
n
Figure 1. DCHWT for a 1-D signal.
the scales 01 correspond to grouping of
coefficients as
234
,, ,,CCCCC




81C5
xx
Cto ,


 
47
xx
CtoC ,






23
xx
oCCt ,




1
x
C,, respectively and
this process continues.
 
0
x
C

For the reconstruction, the DCTs of the subband sig-
nals are concatenated to get the DCT of the fullband
signal. For the first stage of inverse DCHWT illustrated
in Figure 1, the DCTs of the subband signals corre-
sponding to groups C3 and C4 are concatenated. The
resulting group of coefficients is concatenated with the
DCT of subband signal corresponding to group C2, in
the next stage. Again, the resulting group of coefficients
is concatenated with the DCT of subband signal corre-
sponding to group C1, to form the DCT of the fullband
signal.
2.2. Dual Tree Analytic Discrete Cosine
Harmonic Wavelet Transform (ADCHWT)
There are different methods of obtaining the AWT,
which uses the DWT. The straight forward post filtering
approach splits each filter bank output into positive and
negative frequency components using a complex PRFB
acting as a HT though looks simple suffers from nonzero
values in the negative frequency region.
The dual tree complex wavelet transform uses two
DWT trees one for the real part of the analytic signal and
the other for its imaginary part, the HT of the input. The
corresponding scales of the two trees are combined to
achieve the desired analytic WT. This does not require
any complex filters and suffer from any performance
limitation but its computational load is twice that of a
DWT as two DWT trees. The proposed ACHWT is also
realized by a dual tree approach and is shown in the Fig-
ure 2 for 4 scales. Here the DCHWT 4 scales for the
original signal are obtained in the method explained in
Subsection 2.1. The input signal is converted to its HT
and again its DCHWT 4 scales are obtained. Thus the
different scales and their HTs are obtained by simply

A Dual Tree Complex Discrete Cosine Harmonic Wavelet Transform (ADCHWT) and 222
Its Application to Signal/Image Denoising
Hilbert
Transform
()
x
n
ˆ()
x
n
j
j
j
j




DCHWT
DCHWT
()
0
cn
()
1
cn
()
2
cn
()
3
cn
ˆ()
0
cn
ˆ()
1
cn
ˆ()
2
cn
ˆ()
3
cn
ˆ () ()j
00
cn cn
ˆ () ()j
11
cn cn
ˆ () ()j

22
cn cn
ˆ () ()j

33
cn cn
Figure 2. Schematic of the dual tree ADCHWT for a 1D
signal.
converting the input to its HT. Further, Hilbert trans-
formed scales are weighted by j and are combined with
their corresponding scales by summation to get the ana-
lytic harmonic discrete cosine wavelet transform (AD-
CHWT). For reconstruction, the real part of the AD-
CHWT is taken and the procedure is same as given in
Subsection 2.1.
The HT forms an integral part of the ADCHWT and
hence its quality determines the performance of AD-
CHWT. The analytic signal can be realized in the fre-
quency domain by making the negative frequency com-
ponents of the original signal to zero and scaling the
positive components by a factor 2and taking its inverse
FT. The imaginary part of this analytic signal gives the
desired HT of the signal. However, this method suffers
from leakage problem of DFT as the energy from the
negative frequency components would have leaked into
the positive frequency region. Therefore, it is desirable to
realize HT the signal in time domain by convolving the
HT impulse response with the input signal [10]. The im-
pulse response


hn of the HT is given by
 
2
sin π2
2
π
n
hn n
n






(5)
In practice the length of the impulse response is same
as data length. Hence truncating the impulse response
results in Gibbs ripple effect in the frequency response of
the HT. This Gibbs ripple will introduce distortion due to
variation in gain in the passband of the signal. To over-
come this, the HT impulse response has to be windowed
by a smoothing window like Kaiser with an appropriate
smoothing factor.
The shift invariance performance for the proposed
ADCHWT is illustrated for two types of signals viz., an
impulse and a rectangular pulse. The magnitude differ-
ence of the WT coefficients (for different scales) be-
tween original signal and its shifted version are plotted
(Figure 3).
No. Samples
Mag
.
020 4060
-0. 5
0
0.5
010 20 30
-0.5
0
0. 5
0
5
10
15
-0.5
0
0.5
02468
-0.5
0
0.5
020 40 60
-1
-0. 5
0
0. 5
050 100
-0. 5
0
0. 5
01020 30
-1
-0.5
0
0.5
1
051015
-1
-0. 5
0
0.5
No. Samples
No. Samples
No. Samples
Mag
.
(a) (b)
(c) (d)
No. Samples
Mag
.
No. Sa mples
No. Samples
Mag
.
No. Samples
(e) (f)
(g) (h)
Figure 3. Difference in WT indicating energy for Impulse
and pulse. For impulse: (a) Scale-0, (b) Scale-1, (c) Scale-2
(d) Scale-3 For pulse: (e) Scale-0, (f) Scale-1 , (g )Scale-2, (h)
Scale-3 - - - DCHWT, _____ ADCHWT.
It is seen that for the higher scales the magnitude of
the difference between WT coefficients for the original
and shifted inputs (by 4 samples) is higher for the
DCHWT than for ADCHWT both for the impulse and
pulse inputs. Also the energy of this WT difference is
indicated in Table 1. It is seen that with the ADCHWT,
this difference energy is significantly small compared to
that of DCHWT as the latter gets affected by the shift
due to its shift variant nature.
2.3. Two Dimensional Dual Tree ADCHWT
For a 2D signal, the DCT coefficients for the columns are
split in to two groups and their inverse DCT results in
DCTHWT coefficients for the columns. The DCT along
the rows for each scale are taken and grouped. The in-
verse DCT of these groups will result in 2D DCTHWT
(Figure 4(a)). This procedure is repeated for further
scales considering the LL block as input. The procedure
holds good for the real part of ADCHWT of an image.
For the imaginary part of ADCHWT image on hand,

A Dual Tree Complex Discrete Cosine Harmonic Wavelet Transform (ADCHWT) and 223
Its Application to Signal/Image Denoising
Table 1. Error energy between the WT of original and
shifted signal.
WT Type DCHWT ADCHWT
Scale No. For Impulse For Pulse For Impulse For Pulse
0 1.0 0.916 1.0068 0.998
1 0.527 3.29 0.210 0.442
2 0.391 3.27 0.0037 0.231
3 0.069 2.59 0.005 0.204
(a)
02
/


L
H
L
H
2/


L
H
0
IDCT
L
L
LH
H
L
HH
H
L
IDCT
IDCT
IDCT
IDCT
IDCT
scalenextfor
Image
DCT along columns
DCT along
rows
(b)
02/


L
H
L
H
2/


L
H
0
IDCT
L
L
LH
H
L
HH
H
L
IDCT
IDCT
IDCT
IDCT
IDCT
DCT along rows
02/


L
H
L
H
2/


L
H
0
IDCT
L
L
LH
H
L
HH
H
L
IDCT
IDCT
IDCT
IDCT
IDCT
DCT along columns
HT along rows
HT along columns
DCT along rows
scalenextfor
scalenextfor
Figure 4. (a) Schematic for (a) the real part and (b) the
imaginary part of 2D-ADCHWT.
its HT has to be considered. For this to start with, prior to
along the columns of the image are taken and for these
Hilbert transformed columns, the DCTs are taken (Fig-
ure 4(b)).
Further the DCT coefficients are grouped in to two
groups and for each group, inverse DCT is applied to get
the WT scales corresponding to the image columns. For
each scale along the rows, the HTs are taken and for
Hilbert transformed rows, the DCTs are taken. Again
these DCT coefficients are grouped in to two groups and
for each group inverse DCT is applied to get ADCHWT
with scales HL, HH, LL and LH. As the HT has to be
applied column and row wise only once, for higher scales,
that is for splitting LL further, HT should not be applied
and this is indicated in the Figure 3(b) which shows the
absence column and row wise application of HT beyond
LL scale. That is further LL scale decomposition is simi-
lar to that of the real part decomposition.
3. Signal and Image Denoising Using
ADCHWT
Wavelet domain plays an important role in noise sup-
pression. This is because, unlike removal of frequency
components in FT based methods, here no (higher) fre-
quency component is removed which results in smooth-
ing of fast changes or edges. But in wavelet domain,
noise suppression is done in time domain and hence no
scale/frequency is removed unless it is totally not con-
tributing to the signal. In wavelet denoising, in each scale,
those values, which are below a certain threshold are
made zero/modified and the signal is reconstructed with
these modified scales. This is based on the assumption
that the noise is distributed over all scales and their mag-
nitudes will be small. But the problem with wavelet de-
noising is shift variant nature of WT (already been ex-
plained). In WT domain as the signal is reconstructed
with modified decimated scale samples, there will be
glitches as in between samples are removed especially at
higher scales. The solution to this is to use shift invariant/
undecimated WT but this is at the expense of additional
computational load. In view of this, the analytic WT,
which provides shift invariance due to its reduced band-
width by a factor of half, is an appropriate solution. Here
in performing denoising, the threshold for each scale is
found by considering the absolute values of ADCHWT
coefficients. Further, the absolute values of ADCWT are
compared with the estimated threshold to make a deci-
sion about whether a particular WT coefficient has to be
retained/modified. This decision is applied to DCHWT
(real domain) and the different modified scales are used
for the signal reconstruction. In decision making not only
the shift invariant nature of analytic WT but also its good
envelope extraction property also contributes to it. Hence
in some cases, the analytic WT based denoising performs
better than those of shift invariant WT.
4. Simulation Results
The performance of the ADCHWT is shown for a dis-
continuous signal (SNR = 9 dB) of 2048 points, speech
segment (SNR = 10 dB) and an image (SNR = 22 dB).
The noise associated with these is zero mean white
Gaussian noise.
For the discontinuous signal, ADCHWT with 11
scales is considered and the denoising is done for lower 5
scales. For this, hard thresholding is done by using the
standard deviation of the first scale scaled by a factor 6
as the threshold. The hard thresholding is given by
 
real ,
0,
HT
xx
fx x









A Dual Tree Complex Discrete Cosine Harmonic Wavelet Transform (ADCHWT) and 224
Its Application to Signal/Image Denoising
where

HT
f
x is the modified DCHWT for denoising,

is the threshold and
x
is the analytic WT coeffi-
cient value which is complex. ADCHWT showed im-
proved performance as its O/P-SNR as 13.7 dB as against
13.1 dB for DCHWT and the glitches are of reduced
magnitude compared to that of DCHWT (Figures 5(c)
and (d)).
The speech, used is “Kaveriya Ugama Sthana Ko-
dagu” sampled at 22050 Hzand quantized with 16 bits. A
length of 1024 samples is used to generate frames with
50% overlap between successive frames. A 10 scale
ADCHWT is considered for each frame. Further denois-
ing by hard thresholding is done for lower 5 scales using
the standard deviation of the first scale scaled by a factor
7 as the threshold. ADCHWT extracts the signal enve-
lope well (Figures 6 (a), (c) and (d), a typical signal part
is shown by encircling in Figure 6(d)). This results in a
01000 200
0
-1
-0.5
0
0. 5
1
(c)
0 1000 2000
-1
-0.5
0
0.5
1
(a)
No. Samples
01000 200
0
-1
-0.5
0
0.5
1
(b)
Mag
.
0 1000 2000
-1
-0.5
0
0.5
1
(d)
No. Samples
Mag
.
Figure 5. Denoising comparison for discontinuous signal (a)
Clean, (b) Noisy (10 dB), (c) by DCHWT, (d) ADCHWT.
05 10 15
-0.5
0
0. 5
05 10 15
-0. 5
0
0. 5
05 10 15
-0.5
0
0. 5
No. Samples ×10
4 No. Sampl es ×10
4
05 10 15
-0.5
0
0.5
(a)
Mag.
(b)
(c) (d)
Mag.
Figure 6. Denoising Comparison for speech (a) Clean, (b)
Noisy (9dB), (c) DCHWT, (d) ADCHWT.
better output. SNR by 4dB compared to that of DCHWT.
From hearing point of view, both sound somewhat simi-
lar, however DCHWT is having some glitches.
The image is decomposed into three scales with each
scale consisting of four levels (LL, LH, HL and HH). So
for three scales there are 12 levels. Denoising is carried
out for all levels except scale-3, LL level assuming that it
contains sufficiently large wavelet coefficients to repre-
sent the image. For image, a threshold value of 70 which
corresponds to minimum error energy between the origi-
nal and reconstructed image, is found experimentally as
indicated in Table 2. Further, as seen from the Table 2,
the optimum threshold point for DCHWT and ADCHWT
occur at 60 and 70, respectively The output SNR with
threshold value 60 is 18.7128 and 19.2958 for DCHWT
and ADCHWT, respectively. But the output SNR for
threshold value 70 is 18.3551 and 19.50 for DCHWT and
ADCHWT, respectively and for ADCHWT, the output
SNR is better by 1.2 dB compared to that of DCHWT.
This also evident from Figures 7(a), (c) and (d) as the
overall denoising is better for ADCHWT specially in
bringing out the details.
5. Conclusions
A new dual tree Analytic Cosine Harmonic Wavelet
transform was proposed. The analytic DCHWT was re-
alized by applying DCHWT to the original signal and its
Hilbert transform.
For both impulse and pulse input signals, its shift in-
variant property was found to be superior to that of
DCHWT. Its application to noisy discontinuous signal,
speech and image; indicated that due to its shift invariant
and envelope preserving properties in deciding the modi-
fication of WT has resulted in a superior denoising per-
formance than those of DCHWT. The real nature and the
Table 2. Threshold selection criteria for image denoising.
Threshold CHWT RMS Error AHWT RMS Error
10 0.1859 0.1874
20 0.1745 0.1818
30 0.1538 0.1660
40 0.1323 0.1424
50 0.1188 0.1207
60 0.1160 0.1084
70 0.1208 0.1059
80 0.1281 0.1092
90 0.1363 0.1146
100 0.1428 0.1208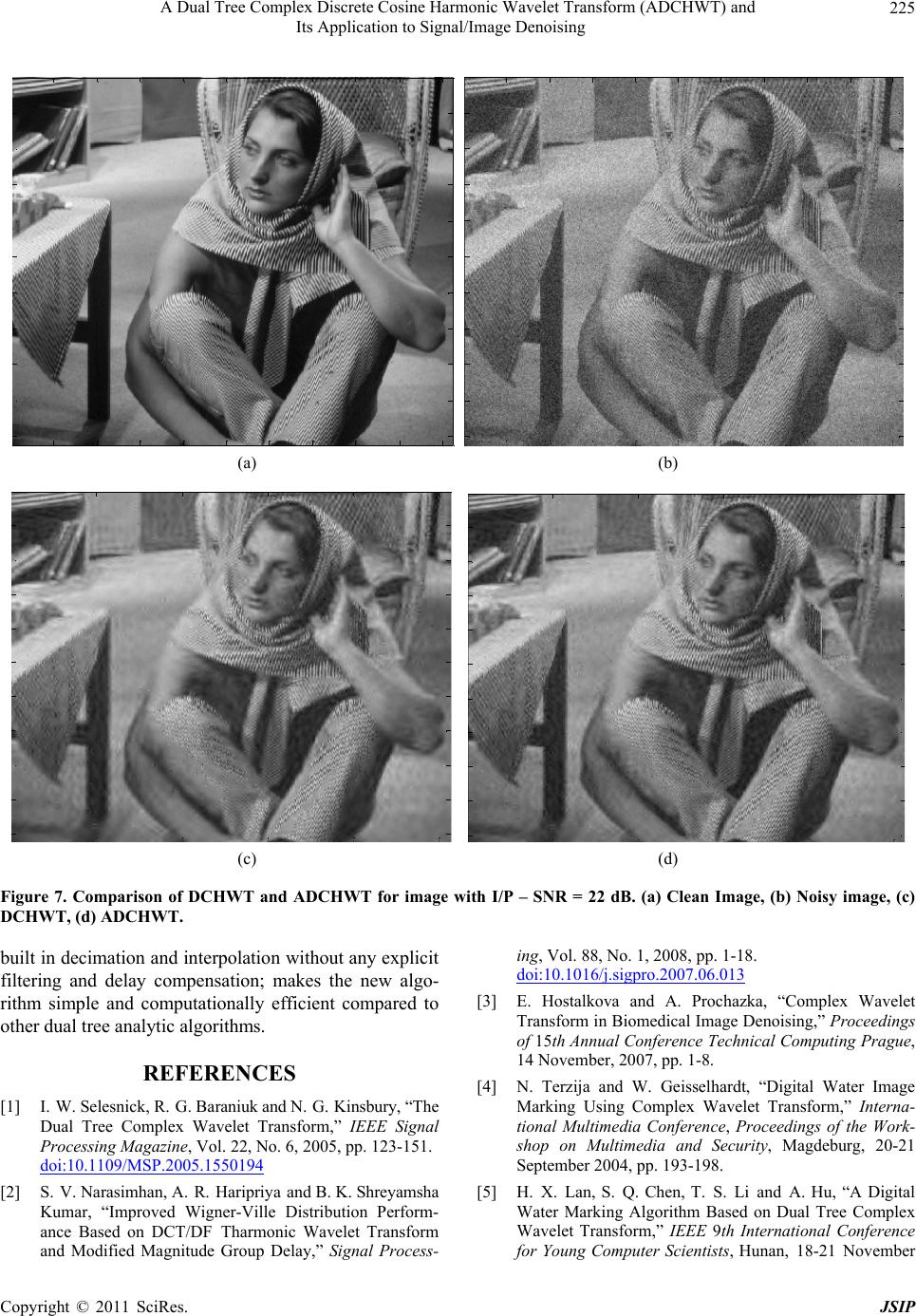

A Dual Tree Complex Discrete Cosine Harmonic Wavelet Transform (ADCHWT) and
Its Application to Signal/Image Denoising
225
(a) (b)
(c) (d)
Figure 7. Comparison of DCHWT and ADCHWT for image with I/P – SNR = 22 dB. (a) Clean Image, (b) Noisy image, (c)
DCHWT, (d) ADCHWT.
built in decimation and interpolation without any explicit
filtering and delay compensation; makes the new algo-
rithm simple and computationally efficient compared to
other dual tree analytic algorithms.
REFERENCES
[1] I. W. Selesnick, R. G. Baraniuk and N. G. Kinsbury, “The
Dual Tree Complex Wavelet Transform,” IEEE Signal
Processing Magazine, Vol. 22, No. 6, 2005, pp. 123-151.
doi:10.1109/MSP.2005.1550194
[2] S. V. Narasimhan, A. R. Haripriya and B. K. Shreyamsha
Kumar, “Improved Wigner-Ville Distribution Perform-
ance Based on DCT/DF Tharmonic Wavelet Transform
and Modified Magnitude Group Delay,” Signal Process-
ing, Vol. 88, No. 1, 2008, pp. 1-18.
doi:10.1016/j.sigpro.2007.06.013
[3] E. Hostalkova and A. Prochazka, “Complex Wavelet
Transform in Biomedical Image Denoising,” Proceedings
of 15th Annual Conference Technical Computing Prague,
14 November, 2007, pp. 1-8.
[4] N. Terzija and W. Geisselhardt, “Digital Water Image
Marking Using Complex Wavelet Transform,” Interna-
tional Multimedia Conference, Proceedings of the Work-
shop on Multimedia and Security, Magdeburg, 20-21
September 2004, pp. 193-198.
[5] H. X. Lan, S. Q. Chen, T. S. Li and A. Hu, “A Digital
Water Marking Algorithm Based on Dual Tree Complex
Wavelet Transform,” IEEE 9th International Conference
for Young Computer Scientists, Hunan, 18-21 November

A Dual Tree Complex Discrete Cosine Harmonic Wavelet Transform (ADCHWT) and 226
Its Application to Signal/Image Denoising
2008, pp. 1488-1492.
[6] A. Jacquin, E. Causevic, R. John and J. Kovacevic,
“Adaptive Complex Wavelet Based Filtering of EEG for
Extraction of Evoked Potential Responses,” International
Conference on Acoustics, Speech and Signal Processing,
Philadelphia, 18-23 March 2005, pp. 393-396.
[7] X. Zhu and J. Kim, “Application of Analytic Wavelet
Transform to Analysis of Highly Impulsive Noises,”
Journal of Sound and Vibration, Vol. 294, No. 4-5, 2006,
pp. 841-855. doi:10.1016/j.jsv.2005.12.034
[8] D. E. Newland, “Harmonic Wavelet Analysis,” Proceed-
ings of Royal Society—Series A, Vol. 444, 1993, pp. 203-
225.
[9] S. V. Narasimhan, M. Harish, A. R. Haripriya and N.
Basumallick, “Discrete Cosine Harmonic Wavelet Trans-
form and Its Application to Signal Compression and Sub-
band Spectral Estimation Using Modified Group Delay,”
Signal, Image and Video Processing, Vol. 3, No. 1, 2009,
pp. 85-99. doi:10.1007/s11760-008-0062-7
[10] N. Basumallick and S. V. Narasimhan, “A Discrete Cosine
Adaptive Harmonic Wavelet Packet and Its Application to
Signal Compression,” Journal of Signal and Information
Processing, Vol. 1, No. 1, 2010, pp. 63-76.
[11] S. V. Narasimhan and M. Harish, “A New Spectral Esti-
mator Based on Discrete Cosine Transform and Modified
Group Delay,” Signal Processing, Vol. 86, No. 7, 2006, pp.
1586-1596. doi:10.1016/j.sigpro.2005.09.002
[12] S. V. Narasimhan and A. Adiga, “Shift Invariant Discrete
Cosine Harmonic Wavelet Transform and Its Application
to Denoising,” IEEE INDICON, Bangalore, 6-8 Septem-
ber 2007.
[13] M. Shivamurti and S. V. Narasimhan, “Analytic Discrete
Cosine Harmonic Wavelet Transform (ADCHWT) and Its
Application to Signal/Image Denoising,” IEEE Interna-
tional Conference on Signal Processing and Communica-
tion, Bangalore, 18-21 July 2010, pp. 1-5.