Open Access Library Journal
Vol.02 No.04(2015), Article ID:68341,13 pages
10.4236/oalib.1101401
Optimization of Force and Power Imposed on Continuous Tandem Cold Rolling Rollers Using a Multiple-Function Genetic Algorithm
Mehdi Safari1*, Mohammadreza Moghoomi2
1Department of Mechanical Engineering, Arak University of Technology, Arak, Iran
2Department of Mechanical Engineering, Daneshpajoohan Higher Education Institute, Isfahan, Iran
Email: *m.safari@arakut.ac.ir, *ms_safari2005@yahoo.com
Copyright © 2015 by authors and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 April 2015; accepted 23 April 2015; published 28 April 2015
ABSTRACT
The amount of energy consumed in the production lines such as cold rolled process is one of the fundamental problems in the energy infrastructure of manufacturing sectors. Accordingly, much attention should be directed towards optimizing the power consumption of production lines using reasonable methods. Furthermore, the powers exerted on such equipment must be modified to find an optimized energy consumption level. This study tries to examine the optimization of forces and powers imposed on the continuous tandem cold rolling rollers of metal sheets using MATLAB and genetic algorithm. Firstly, some relationships and calculations of rolled metal sheets are analyzed. Then parameters, such as percentage of thickness reduction, mean pressure, yield stress, power of rollers and exerted torque, are calculated. All the governing relationships are programmed using MATLAB software. Having compared the mentioned two methods, genetic algorithm is used to determine the optimal required power. The results show that the optimized powers generated by genetic algorithm method are in good agreement with experimental observations. Also, the powers of rolling rollers and standard deviations of powers are calculated and, then, the two functions are compared and the optimum point between them is optimized.
Keywords:
Tandem Cold Rolling, Power of Roller, Genetic Algorithm, Optimization of Force
Subject Areas: Mechanical Engineering

1. Introduction
The main purpose of the cold rolling process, in addition to obtaining good mechanical properties, is to achieve precision and very low thicknesses, the subject which is not possible in the hot rolling process. Nowadays, most cold rolling lines are designed continuously that are made up usually from 4 to 6 rolling shelves with four-roller. Surface of obtained cold-rolled sheets is harder and more smoothly than obtained hot-rolled sheets [1] . Sheets and belts obtained from cold rolling are manufactured in various thickness of less than 0.1 mm to 6 mm as coils or sheets, by mutual rolled or consecutive shelves. Also, in the cold rolling process, 25% to 90% reduction in thickness can be achievable [2] . In the cold rolling process, the main parameters such as thickness reduction at each stage of rolling, the size of the total reduction in thickness, width and thickness of the current sheet, constant thickness across the sheet, straightness of sheet surface, lubricate operations, tensile stresses of behind and front of the sheet, torque and each shelf rollers force, speed and coordination between the shelves should be carefully controlled in order to achieve a high quality sheet [3] . So far, many efforts have been made for metal forming, especially for cold-rolled steel sheets. In 2001, Venkada et al. [4] calculated the power consumption of rollers in the cold rolled process. Their results showed that the calculated reduction percentage in thickness of the sheet with 6 shelves roller, was in good agreement with report of Roberts. In 2000, Venga et al. [5] tried to achieve optimal planning design for continuous cold rolling process. They designed an algorithm based on the genetic optimization with the aim of optimizing the stress and speed. The results of distribution of power, stress and sheet flatness showed that optimized results were in good agreement with experimental observations. In 2008, Yang et al. [6] showed that the results of optimization algorithms were satisfied and good in comparison with other programs. In 2009, Vining et al. [7] considered the amount of carbon and carbide and reduction in the amount of rolling work as inputs of calculations to design a model that was able to predict at the same time and faster in an engineering environment. The output obtained from their studies suggested a set of parameters that were in a good agreement with experimental results. In 2004, Nivowski et al. [8] suggested an approximate analytical solution by introducing a nonlinear mathematical model for oscillation system of continuous rolling racks. Their study showed that the results of proposed analytical solution were comparable with rolling experimental parameters. In 2005, Weng et al. [9] by introducing an intelligent search mechanism for optimizing the planning with the assessment limitation of roll and the combination function of stress and distribution of power, achieved the maximum amount of rolling-work sheet safety. The model presented in this study, was able to solve multi-objective problems. In 2008, Pitner et al. [10] proposed a new method that used the Rikaty equation to control rolling process. In 2008, Dean et al. [11] used point-to-point, linear, quadratic method for optimal control of continuous cold rolling. To control the rollers, they used a new strategy to overcome the existing limitations, by designing multi-input and multi-output functions. Their results showed that the thickness of the output rolled sheet was between 0.5 onto 0.8 percent less than other studies, and caused stability of the rolling process. In Figure 1, schematic of the cold rolling process is shown.
Figure 1. Schematics of the cold rolling process.
The amount of energy consumed in the production lines such as cold rolled process is one of the fundamental problems in the energy infrastructure of manufacturing sectors. Accordingly, much attention should be directed towards optimizing the power consumption of production lines using reasonable methods. Furthermore, the powers exerted on such equipment must be modified to find an optimized energy consumption level. This study tries to examine the optimization of forces and powers imposed on the continuous tandem cold rolling rollers of metal sheets using MATLAB and genetic algorithm. Firstly, some relationships and calculations of rolled metal sheets are analyzed. Then parameters, such as percentage of thickness reduction, mean pressure, yield stress, power of rollers and exerted torque, are calculated. All the governing relationships are programmed using MATLAB software. Having compared the mentioned two methods, genetic algorithm is used to determine the optimal required power. The results show that the optimized powers generated by genetic algorithm method are in good agreement with experimental observations. Also, the powers of rolling rollers and standard deviations of powers are calculated and, then, the two functions are compared and the optimum point between them is optimized.
2. Genetic Algorithm
Genetic algorithm is a learning approach based on biological evolution which is taken from Darwinian Theory of evolution in 1859. In 1970, the main idea of this method is introduced by Heland, Deyjon and Gowgeldberg. These methods are also called with the name of the evaluation algorithm too.
2.1. Characteristics of Genetic Algorithm
In genetic algorithms, populations of points are searched in parallel (instead of a point). Also probability transition rules are used (instead of deterministic transition rules). In the genetic algorithm, it does not require to information about the differentiable of the objective function (that is enough for the problem to define a fitness function). In addition, the genetic algorithm is useful for noisy environments and can be easily applied to multi- objective problems. This algorithm is located on the class of random optimization algorithms. It is especially used for complex optimization problems with an unknown search space. In general, we can say that the genetic algorithm has the following characteristics:
1) Instead of encoding parameters, encoding set of them.
2) Instead of searching for a spot, looking for population of points.
3) Instead of using derivations or other auxiliary information, directly using information available on existing results.
4) In this type of algorithms, instead of absolute rules, using the probability rules to change.
5) In the genetic algorithm, instead of searching particular hypothesis or simple and complete ones, makes the new hypothesis by changing and combining sequential components, into the best possible hypothesis.
6) At each step, a set of assumptions that are called population, are derived by replacing part of the current population with the children who have acquired the best available hypothesis.
7) In properties of a new generation, except in exceptional circumstances where mutations may occur, usually the new generations are more compatible with nature [12] .
2.2. Optimizing Method by Genetic Algorithms
Genetic algorithms approach to optimize problems through a processs similar to natural selection methods and natural genetic in the biological sciences. These algorithms are widely used in the past decade as search and optimization tools in various fields such as business, science and engineering. Flowchart of genetic algorithm to optimize is shown in Figure 2.
In the genetic algorithm that is used in this research, three key issues can be optimized including power consumption, standard deviation of power and optimization of these two functions together. Finally, the variables of the problem are the thicknesses of the entrance and existence of the five shelves continuous cold rolling and tensile forces between shelves. In genetic algorithms, it is necessary for optimizing that started a set of solutions (chromosomes) with initial value and investigated the problem again, and then by using a fitness function, evaluated the existing problem. Accordingly the best chromosomes are selected in the mating pool and treated on there with a mutation occurs, and then a series of solutions are presented. In this paper, for calculation of cold
Figure 2. Flowchart of genetic algorithm [13] .
rolling, initially the system inputs are defined as follows: Input thickness of sheet, output thickness of sheet, friction coefficient of rollers, radius of rollers, width of the sheet and tensile force between roller and shelf. Then all the parameters listed above have been considered the coming three basic purposes:
1) Optimizing rolling power of shelves.
2) Optimizing the standard deviation of the power consumption of rollers.
3) Finding optimum points between the above two functions.
3. The Analytical Relations of the Cold Rolling Process
Analytical calculations in this paper are based on the Ston, Parkinz and Okeland theories, and considered process is 5-shelfrolling. Using the relations, the value of power, torque and eventually power of rolling is calculated. The percent of reduction in sheet thickness in each shelf is calculated with Equation (1). Also, the average value of tensile yield stress comes out from Equations of (2) and (3).
 (1)
(1)
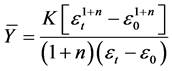 (2)
(2)
In Equation (1), r is assumed reduction percent in the thickness of sheet in each shelf. hin and h1 are the input and output thickness of sheet on the shelves respectively. Also, in Equation (2) 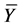 is the average value of tensile yield stress. It should be noted that in the rolling and other metal forming processes, for calculation of force and energy of deformation variable yield stress of the plate can be replaced with average yield stress. In the Equation (2), K and n are the coefficients of the resistance and work hardening of steel respectively that can be obtained from Ludovic equation which are available from charts of the stress-strain behavior of steels.
is the average value of tensile yield stress. It should be noted that in the rolling and other metal forming processes, for calculation of force and energy of deformation variable yield stress of the plate can be replaced with average yield stress. In the Equation (2), K and n are the coefficients of the resistance and work hardening of steel respectively that can be obtained from Ludovic equation which are available from charts of the stress-strain behavior of steels. 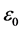 is primary strain and
is primary strain and  is plane strain.
is plane strain.
Equation (3) is used to calculate the average yield stress. In this equation, 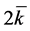 is the average yield stress, which in the plane strain conditions and its relationship to
is the average yield stress, which in the plane strain conditions and its relationship to  is as follows:
is as follows:
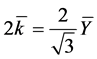 (3)
(3)
Equation (4) is used to calculate the mean pressure Pm of rollers. In this relation hm is the average value of the input thickness and output thickness of each shelf and μ is the friction coefficient of process and also Ld is the length of plastic region, and σm is the average stress.
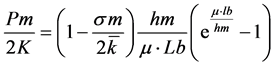 (4)
(4)
Ludovic equation is presented in Equation (5). In this equation, ε is the plane strain and the coefficients of K and n, are extracted from the stress-strain curve [14] .
 (5)
(5)
As the rolling process that is investigated in this paper has pre-tensile and post-tensile stresses, then average stress is calculated from Equation (6). In this equation, σft is the pre-tensile stress and σbt is the post-tensile stress.
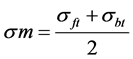 (6)
(6)
The roller force can be calculated from Equation (7).
 (7)
(7)
In the Equation (7) 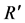 is the roller radius after deformation, Δh is difference between the entry and exit thickness of rolled sheet, W is plate width and Pm are the average pressure. According to Equation (8) power calculation is presented in terms of the width of sheet as follows:
is the roller radius after deformation, Δh is difference between the entry and exit thickness of rolled sheet, W is plate width and Pm are the average pressure. According to Equation (8) power calculation is presented in terms of the width of sheet as follows:
 (8)
(8)
In the Equation (8) 


Due to the presence of two rollers on each shelf (rolling stage), the torque created around the center of each rollers will be calculated as Equation (10).

In Equations (9) and (10), F is the force of Roller, W is the width of sheet, M is the torque and C is a constant that is considered to be 0.4 for cold rolling process.
Finally, in Equation (11) the power of rolling can be calculated. In this equation P is the Roller power, M is the torque and ω is the angular velocity.

In Figure 3 schematic of a continuous cold rolling process is shown.
4. Optimization Procedure
Main goal of this article is using a genetic algorithm to optimize the rolling process in 5-shelf cold rolling. In this study, the output thickness of each shelf and tensile forces between the shelves are assumed as variable parameters that should be optimized. In the optimization procedure, Equations of (12) and (13) are used as objec-
Figure 3. Schematic of a continuous cold rolling process.
tive functions and using genetic algorithm toolbox of Matlab software variable parameters are optimized. In the optimization investigations, the population and number of generations should be defined. In this paper combined population of 30 people and a maximum of 100 generations are assumed. Therefore, two objective functions are as follow:


In Equations (12) and (13) the power values and standard deviations of powers are considered to be optimized. In Equation (13), Pd is the roller power (KW) and the standard deviation is used to optimize it. The values of variable parameters of the cold rolling process are obtained from experimental tests. Therefore, the actual final amount of entry and exit thicknesses of the sheet, and the coefficients K and n are calculated as follows:
In Table 1, the actual radius of the rollers and in Table 2, the coefficients of friction in the rollers of each shelf are presented. In the continuous cold rolling process, the experimental Range of some basic parameters is as shown in Table 3 [16] . Since the variables of the problem are the characteristics such as input and output thicknesses in each shelf and tensile forces between shelves, therefore the percentage of reduction in sheet thickness at each cold rolled shelf is accessible through standard tables. In Table 3, reduction of sheet thickness in each shelf is presented. Upper limit is the maximum allowable reduction in thickness and lower limit indicates the minimum allowable thickness of shelves.
In Table 4, the tensile forces of the shelves that are taken from the standard are shown. Also, in Table 5, the maximum power consumption of each shelf is presented. After programming in MATLAB software, the results of average yield stress of the plate, sheet thickness, average distribution of tensile stress in each shelf, average thickness of the output and input sheets, distribution of tensile force between the shelves, the torques in rolling stages, average pressure of shelves, tensile force distribution between the shelves according to the Stone’s theory, actual (real) consumption power of each cold rolling shelf, average optimized power and a comparison between powers in both actual and optimized modes are presented in Figures 4-13. In these figures, the horizontal axis represents the five shelves of cold rolling process. In Figure 4, the distribution of the average yield stress can be seen in each shelf. The maximum stress is occurred in the last stage of rolling (the fifth shelf) and its value is 700 MPa. It should be mentioned that the average yield stress of sheet increases due to work hardening.
In Figure 5, the value of sheet thickness in each shelf is shown. As it is seen maximum value of thickness is in the first shelf and the minimum value of thickness is in the fifth shelf. In Figure 6, the average distribution of tensile stress in each shelf is presented. As it is seen maximum value of tensile stresses is occurred in the fifth shelf rollers with the value of 606 MPa.
Figure 7 represents the average thickness of the output and input sheets which the highest average thickness is seen in the first shelf (2.16 mm). In Figure 8 and Figure 9, the distributions of tensile force between the shelves and the torques in rolling stages are shown respectively. As can be seen, the maximum tensile force occurs in shelves 2 (6851.3 tones) and 3 (6771.9 tones). As the largest percentage of decrease in the thickness of the roller shelves is occurred in the first shelves then the torque created in the first shelf has the maximum value in Figure 9.
In Figure 10, the average pressure of shelves is shown. As can be seen, the minimum value is in the first shelf
Table 1. Actual radius of the rollers (mm).
Table 2. Coefficients of friction in the rollers.
Table 3. The reduction of sheet thickness in each shelf (%).
Table 4. Tensile forces of the shelves.
Table 5. Maximum power consumption of each shelf.
Figure 4. The distribution of the average yield stress in each shelf.
Figure 5. The value of sheet thickness in each shelf.
Figure 6. The average distribution of the tensile stress.
Figure 7. The average thickness.
Figure 8. The distribution of tensile force between the shelves.
Figure 9. The torque created in rolling.
Figure 10. The average pressure of shelves.
Figure 11. The tensile force distribution between the shelves according to the Stone’s theory.
Figure 12. The actual (real) consumption power of each cold rolling shelf (KW).
Figure 13. 
Figure 14. A comparison graph of powers in both actual and optimized.
(551 Mpa) and the maximum value is in the fifth shelf (1003 MPa). Figure 11 shows the tensile force distribution between the shelves according to the Stone’s theory. As can be seen in this figure, the maximum rotational torque is occurred in the first shelf and minimum rotational torque is occurred in the fifth shelf. Also Figure 12 shows the actual (real) consumption power of each cold rolling shelf. It can be seen in this figure that the maximum power is related to third shelf with a value of 3005 kW. Figure 12 and Table 6, are shown the actual and optimized consumption power in the continuous cold rolling factory.
In Figure 13 optimized consumption power and standard deviation is presented. As it is seen the average optimized power is 911 kW, and variance amount of optimized consumption power is 1660 kW, and accordingly, the results obtained of the genetic algorithm represents that standard deviation of power is 402 kW. The results show that by optimizing the consumption power, power of production line will be reduced by 48% and this result is in good agreement with experimental observations. Obviously, the average value of consumption power is reduced with the same value after optimization. In Figure 14, a comparison between actual and optimized powers is shown. As it is seen, in the shelves of 2, 3 and 4 which have the highest power for reducing the thickness of sheet under rolling process, the actual consumption powers are 2445, 2960 and 2047 kW respectively, while after optimization these values have been reduced to 1189, 1449 and 935 kW respectively.
To optimize consumption power and standard deviation of power, two functions are defined as bellow:
Minimum of power: Object 1.
Standard deviation of power: Object 2.
The relationship between these two functions is presented in Equation (14).

For using Equation (14) weighted coefficient of each function must be defined in the computing of Genetic Algorithm. In the Genetic Algorithm according to the importance of both functions (power and standard deviation), the weighted coefficient of 0.5 is selected for them. It should be noted that according to Equation (14), not only the power and standard deviation of power are optimized separately but also the two functions have been optimized comparatively. One of the important parameters that should be checked in the cold rolling process is the percentage of thickness reduction of output sheet from each shelf. In Table 7 the optimized thicknesses for each shelf that is extracted from the Genetic Algorithm are presented.
In Figure 15, a comparison of thickness of the sheet after rolling in each shelf between actual and optimized states is shown. In Figure 16, percentage of thickness reduction on each shelf before and after optimizing process is shown.
Table 6. The values of actual and optimized powers in the cold rolling process.
Table 7. The optimized thicknesses extracted from the Genetic Algorithm (in mm) are as following.
Figure 15. The comparison between the thicknesses of the sheets after rolling on each shelf in two actual and optimized modes.
Figure 16. The percentage of thickness reduction on each shelf, before optimizing (real).
5. Conclusion
Energy optimization in continuous cold rolling process is depending on factors such as optimization, the tensile force among shelves, consumption power, and percentage of thickness reduction in sheet. For this purpose in this paper, using cold-rolling production line variables of the integrated steel production of Mobarakeh Company (Isfahan, Iran), with rolling engineering relations and programming in MATLAB software, power consumption was calculated and then standard deviation of power was optimized. The result indicated that with optimizing the con- sumption power, the power was reduced as 48.24% in continuous cold-rolling (Tandem) production line of sheet.
Cite this paper
Mehdi Safari,Mohammadreza Moghoomi, (2015) Optimization of Force and Power Imposed on Continuous Tandem Cold Rolling Rollers Using a Multiple-Function Genetic Algorithm. Open Access Library Journal,02,1-13. doi: 10.4236/oalib.1101401
References
- 1. Moshksar, M. (2013) Rolling Engineering Principles. 3rd Edition, Shiraz University Press, Shiraz, 20.
- 2. Miyake, H., et al. (1985) Advanced Fully Continuos Tandem Cold Rolling Mill for Thin Gauge Steel Strip. Proceedings of the International Conference Organized by the Institute of Metal, Advances in Cold Rolling Technology, 38.
- 3. Yuen, W.Y., et al. (1985) Thermal Effects in Cold Rolling. Proceedings of the International Conference Organized by the Institute of Metal, Advances in Cold Rolling Technology, 57.
- 4. Venkata Reddya, N. and Suryanarayanaa, G. (2001) A Set-Up Model for Tandem Cold Rolling Mills. Journal of Materials Processing Technology, 116, 269-277.
http://dx.doi.org/10.1016/S0924-0136(01)01007-X - 5. Wanga, D.D. and Yuen, W.Y.D. (2000) Toward a Heuristic Optimum Design of Rolling Schedules for Tandem Cold Rolling Mills. Engineering Applications of Artificial Intelligence, 13, 397-406.
http://dx.doi.org/10.1016/S0952-1976(00)00016-6 - 6. Yang, J. and Che, H. (2008) Algorithm-Based Optimization Used in Rolling Schedule. International Journal of Iron and Steel Research, 15, 18-22.
http://dx.doi.org/10.1016/S1006-706X(08)60024-2 - 7. Winninga, M. and Brahmeb, A. (2009) Prediction of Cold Rolling Texture of Steels Using an Artificial Neural Network. Computational Materials Science, 46, 800-804.
http://dx.doi.org/10.1016/j.commatsci.2009.04.014 - 8. Świątoniowskib, A. and Bara, A. (2004) Interdependence between the Rolling Speed and Non-Linear Vibrations of the Mill System. Journal of Materials Processing Technology, 155-156, 2116-2212.
- 9. Wang, D.D. and Tieu, A.K. (2005) Computational Intelligence-Based Process Optimization for Tandem Cold Rollin. Materials and Manufacturing Processes, 3, 479-496.
http://dx.doi.org/10.1081/AMP-200053535 - 10. Pittner, J. and Simaan, M.A. (2008) Control of a Continuous Tandem Cold Metal Rolling Process. Control Engineering Practice, 16, 1379-1390.
http://dx.doi.org/10.1016/j.conengprac.2008.03.009 - 11. Pittner, J. and Simaan, M.A. (2008) Optimal Control of Tandem Cold Rolling Using a Pointwise Linear Quadratic Technique with Trims. Journal of Dynamic Systems, Measurement, and Control, 130, 11 p.
- 12. Zandieh, M. (2013) Genetic Algorithm. Version PDF, 31.
- 13. Safari, H. and Masuodi, A. (2012) Optimization of Plat-Fin Heat Exchanger with Genetic Algorithm. Journal of Aerospace Mechanics, 8, 55-68.
- 14. Aghadavoodi, F., Golestanian, H. and Negahbani, N. (2011) Optimization of Reduction Setting and Inter-Stand Tensions for Tandem Cold Mills Using Genetic Algorithm. Journal of Solid Mechanics in Engineering, 3, 55-67.
- 15. Moshksar, M. (2013) Rolling Engineering Principles. 3rd Edition, Shiraz University Press, Shiraz, 335.
- 16. Moshksar, M. (2013) Rolling Engineering Principles. 3rd Edition, Shiraz University Press, Shiraz, 9.
List of Symbols
F: Tensile force between the shelves (N)
hin: Input thickness of sheet on the shelves (mm)
K: Extracted from the graph of (Mpa) stress-real strain of stress experiment
M: The torque created in rolling N∙m
Pm: The average pressure of shelves (Mpa)
R: Radius of the roller (mm)

r: Percent reduction in the thickness
W: Plate width (mm)






ω: Angular velocity (Rad/s)
NOTES
*Corresponding author.




















