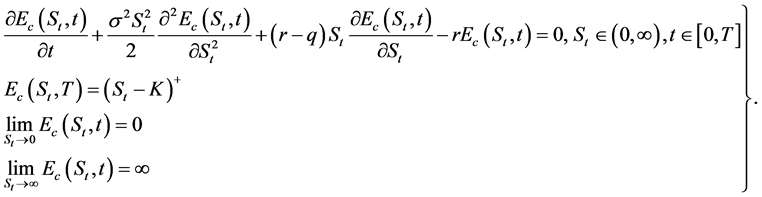Received 28 March 2015; accepted 13 April 2015; published 17 April 2015

ABSTRACT

In this paper we present an alternative approach for the solution of the Black-Scholes partial differential equation for European call option which pays dividend yield using the modified Mellin transform method. The approach used in this paper does not require variables transformation. We also extend the modified Mellin transform method for the valuation of European call option which pays dividend yield. The numerical results show that the modified Mellin transform is accurate, mutually consistent and agrees with the values of the Black-Scholes model.

Keywords:

Black-Scholes Partial Differential Equation, Dividend Yield, European Call Option, Modified Mellin Transform Method

Subject Areas: Mathematical Analysis, Mathematical Economics

1. Introduction

Option valuation has been studied extensively in the last three decades. An option on an underlying asset is defined as an asymmetric contract that entitles the holder to buy or sell the underlying asset at a specified price on or before a certain date. The underlying asset includes stocks, foreign currencies, and stock indices, just to mention a few.

European options give the holder the right to trade the underlying asset in the future at a previously agreed price. European options can be exercised only on the expiry date. American options give the holder more rights than their European equivalent and can therefore be more valuable, and they can never be less valuable. The main point of interest with American-style options is deciding when to exercise. Most of options traded on exchange are of American type and therefore the valuation problem for American options has received a lot of attention.

Until 1973, the valuation of an option was done by little more than guesswork. Black and Scholes [1] published their seminar work on options valuation, in which they described a mathematical frame work for finding the fair price of a European option by means of a non-arbitrage argument to describe a second order partial differential equation which governs the evolution of the option price with respect to the time to expiry and the price of the underlying asset. Since then, there has been an explosive growth, both in the trading and the study of options of various kinds. Despite the success of the Black-Scholes model on hedging and pricing contingent claims, Merton [2] noted early that options quoted on the markets differ systematically from their predicted values, which led up to questioning the distributional assumptions based on geometric wiener process.

The Mellin transform in the theory of option pricing was introduced by Panini and Srivastav [3] . They derived the expression for the free boundary and price of an American perpetual put as the limit of finite lived options. Nwozo and Fadugba [4] considered the Mellin transform method for the valuation of some vanilla power options with non-dividend yield. They extended the Mellin transform method to derive the price of European and Ame- rican power put options with non-dividend yield. They also derived the fundamental valuation formula known as the Black-Scholes model using the convolution property of the Mellin transform method. Jódar et al. [5] considered a new direct method for solving the Black-Scholes equation using the Mellin transforms. F. Al Azemi et al. [6] obtained an analytical solution of the Black-Scholes equation for the European and the American put options. For mathematical backgrounds, transform methods in the theory of options valuation and some numerical methods for options valuation see [7] - [12] just to mention a few.

In this paper, we shall consider a new approach which does not require variables transformation for the solution of homogeneous Black-Scholes partial differential equation for European call option with dividend yield using the modified Mellin transform proposed by Frontczak and Schöbel [13] .

The structure of the paper is organized as follows. In the next section, we give an overview of the most fundamental ideas and mathematical tools needed for the Mellin transforms. We also present the most relevant properties of the Mellin transforms. Section 3 presents a new approach for the solution of the homogeneous Black- Scholes partial differential equation for European call option which pays dividend yield. Section 4 presents the numerical experiments and discussion of results. Section 5 concludes the paper.

2. Mellin Transform and Its Fundamental Properties in the Theory of Option Valuation

Let be a function defined on the positive real axis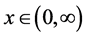. The Mellin transformation denoted by is the operation mapping the function into the function 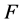defined on the complex plane by the relation

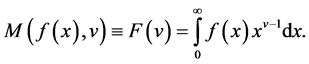(1)

The function 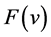is called the Mellin transform of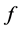. In general, the integral does exist only for complex values of 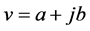such that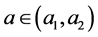, where 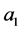and 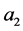depend on the function 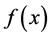to transform. This introduces what is called the strip of definition of the Mellin transform that will be denoted by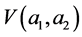. In some cases, this strip may extend to half-plane 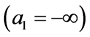or 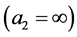or to the complex v-plane and.

Conversely, the inversion formula of (1) is defined as

(2)

where the integration is along a vertical line through.

Some of the basic fundamental properties of the Mellin transforms are detailed below.

If is defined on the positive real axis, then the following properties hold.

a) Shifting property

(3)

b) Scaling property

(4)

c) The Mellin transform of derivatives

(5)

where the symbol is defined for k integer by:

Equations (3) and (6) can be used in various ways to find the effect of linear combination of differential operator such that, k, m integers. The most remarkable results are

(6)

where, k a positive integer and.

3. The Homogeneous Black-Scholes Partial Differential Equation for European Call Option with Dividend Paying Stock in the Domain of the Modified Mellin Transform Method

Let us consider the homogeneous Black-Scholes partial differential equation for European call option which pays dividend yield with the initial and boundary conditions given by

(7)

where is the volatility, r is a risk-free interest rate, K is called the strike price, and T is the maturity date. It is a known fact that the partial differential equation in (7) has a closed form solution obtained after several change of variables and solving certain related diffusion equations. This procedure is not applicable in the vector framework where is a vector and, r are matrices.

Now, observe that

(8)

for any on where is called fundamental strip, the Mellin transform for European call option does not exist since the integral does not converge. Here we shall make use of the modified Mellin transform.

The modified Mellin transform for the price of European call option is defined as

(9)

and the inversion formula for the modified Mellin transform is given by

(10)

Taking the modified Mellin transform of the Black-Scholes partial differential equation for European call option in (7), we have that

(11)

Using the properties of the Mellin transforms, we have the following modified Mellin transforms

(12)

Substituting (12) into (11) and simplifying further yields

(13)

Integrating (13) yields

(14)

Setting, then (14) becomes

(15)

where is a constant of integration to be determined and it is defined as

(16)

can be obtained by taking the modified Mellin transform of the initial condition of the form

(17)

then we have

(18)

Using Equations (15), (16) and (18), we have that

(19)

The modified Mellin inversion of (19) is obtained as

(20)

A New Direct Approach for the Solution of the Black-Scholes Partial Differential Equation for European Call Option with Dividend Paying Stock

An alternative approach for the solution of the homogeneous Black-Scholes partial differential equation for the European call option with dividend paying stock is summarized in the theorem below:

Theorem 3.1.

Let the price of a European call option denoted by be Mellin transformable and continuous, then

for is a solution of the homogeneous Black-Scholes partial differential equation for the European call option with dividend yield given by

Proof: We want to prove that the expression (20) is a solution of the Black-Scholes partial differential equation for European call option given by (7). Let us assume that

(21)

Substituting (21) into (20) yields

(22)

Substituting into, then we have that

(23)

Since is Mellin transformable and continuous, setting then (22) becomes

(24)

Equation (22) is well defined and satisfies (24).

Using the definition of the modified Mellin transform, then

(25)

and for we have that

(26)

Using the differentiation theorem of parameter integrals [14] and the fact that

(27)

Then it follows that upon differentiation of (22), we have that

(28)

Substituting (22) and (28) into the Black-Scholes partial differential equation for European call option given by (7), we have

(29)

Hence the price of the European call option denoted by and given by (20) is a solution of (7) and the result is established.

4. Numerical Experiment

Experiment 1

We consider the valuation of European call option with nine months to expiration via the modified Mellin transform method. The stock index is 95, the exercise price is 90, the risk-neutral interest rate is 0.2 per year, the dividend yield is 0.06 per year and the volatility is 0.3 per year.

The parameters are:

The results obtained are displayed below.

The value of the analytic pricing formula is 16.943.

The modified Mellin transform put price is obtained as 16.943.

Experiment 2

We consider the performance of the modified Mellin transform method against the “true” Black-Scholes model and binomial model for the valuation of European calloption which pays dividend yield q with the following parameters.

The results obtained are shown in the Table 1 below.

Discussion of Results

From Experiment 1, we can see that the price of European call option via the modified Mellin transform method and analytic option pricing formula are the same. Table 1 shows the effect of dividend yield on the performance of the modified Mellin transform method against the “true” Black-Scholes model and binomial model for the valuation of European call option. The results obtained show that the higher the dividend yield, the smaller the values of the three methods. The modified Mellin transform is more accurate than the binomial model when pricing European call option with dividend yield. Hence the modified Mellin transform is mutually consistent and agrees with the values of the Black-Scholes model.

5. Conclusion

Financial modeling in the area of option valuation involves detailed knowledge about stochastic processes describing the asset payoffs. In this paper, we developed an alternative approach for the solution of the homogeneous Black-Scholes partial differential equation for European call option with dividend yield using the modified Mellin transform method. The approach used in this paper does not require variables transformation. The modified Mellin transform method seems likely to be quick and accurate when pricing European call option with dividend yield.

Cite this paper

Sunday Emmanuel Fadugba,Adedoyin Olayinka Ajayi, (2015) Alternative Approach for the Solution of the Black-Scholes Partial Differential Equation for European Call Option. Open Access Library Journal,02,1-8. doi: 10.4236/oalib.1101466

References