Open Access Library Journal
Vol.02 No.04(2015), Article ID:68298,8 pages
10.4236/oalib.1101404
Transient Solution of M/M/2/N System Subjected to Catastrophe cum Restoration
Dhanesh Garg
Department of Mathematics, Maharishi Markandeshwar University, Mullana, India
Email: dhaneshgargind@gmail.com
Copyright © 2015 by author and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 March 2015; accepted 9 April 2015; published 14 April 2015
ABSTRACT
In this paper, we study the distribution of the number of times that a finite capacity with equal servers Markovian queuing model catastrophic-cum-restorations reaches its capacity in time t. The occurrence of a catastrophe makes the system empty instantly but the system takes its own time to be ready to accept new customers. This time is referred to as “restoration time”. The aforesaid distribution is obtained as a marginal distribution of the joint distribution of the number of customers in the system at time t and the number of times system reaches its capacity in time t under the conditions of catastrophes and restorations.
Keywords:
Catastrophes, Markovian Queue, Restoration, Transient State, Laplace Transform
Subject Areas: Mathematical Statistics, Operational Research, Statistics

1. Introduction
Catastrophe modeling and analysis had been playing a vital role in various areas of science and technology. Chao [1] has modeled computer networks with a virus by queuing networks with catastrophes. Kumar et al. [2] and [3] studied the transient behaviour of the M/M/2 queue with catastrophes. Di Crescenzo et al. [4] made a continuous approximation of M/M/1 queue with catastrophe. Jain and Kumar [5] and [6] obtained the transient solution of a catastrophic-cum-restorative queueing problem with correlated arrivals and variable service capacity and special case of [7] - [10] . In all the above mentioned studies, the researchers have obtained the state probabilities in one way or the other and have computed various measures of performance. In this paper, the occurrence of a catastrophe makes the system empty instantly whenever the system is not empty but the system takes its own time to ready to accept new customers. This time is referred to as “the restoration time”. The system subjected to catastrophes must take some time for its restoration after the occurrence of a catastrophe. We have obtained explicitly the distribution of the number of times the system reaches its capacity in time t under the effects of catastrophe and restoration.
2. The Queue Model
We consider an M/M/2/N queueing system having two homogenous servers with FCFS discipline subject to catastrophes and restorations. The customers arrive at a counter in accordance with a Poisson process with mean arrival rate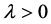 . Each server serves one customer at a time if available. The service time distribution of a customer is negative exponential with mean rate
. Each server serves one customer at a time if available. The service time distribution of a customer is negative exponential with mean rate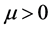 . The queuing process starts at time zero with zero state of the system. Catastrophes occur according to Poisson process with mean rate
. The queuing process starts at time zero with zero state of the system. Catastrophes occur according to Poisson process with mean rate 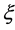 only when the system is not empty. The occurrence of a catastrophe destroys all the customers in the instants and affects the system as well. The system will require some sort of time to restarts in a normal way, which is taken as restoration time. The restoration times are independently, identically exponentially distributed with parameter
only when the system is not empty. The occurrence of a catastrophe destroys all the customers in the instants and affects the system as well. The system will require some sort of time to restarts in a normal way, which is taken as restoration time. The restoration times are independently, identically exponentially distributed with parameter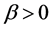 . The customers arrive in the system during the restoration time as usual.
. The customers arrive in the system during the restoration time as usual.
We define joint probability distribution
 (1)
(1)
where 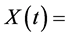 the number of times the system reaches its capacity in time t;
the number of times the system reaches its capacity in time t;
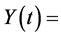 the number of customers in the system at time t;
the number of customers in the system at time t;
 the prob. that there are zero customers in the system at time t without the occurrence of catastrophe;
the prob. that there are zero customers in the system at time t without the occurrence of catastrophe;
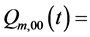 the prob. that there are zero customers in the system at time t with the occurrence of catastrophe destroying all the customers.
the prob. that there are zero customers in the system at time t with the occurrence of catastrophe destroying all the customers.
3. Time Dependent Probabilities
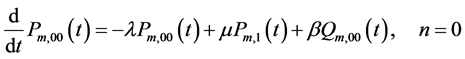 (2)
(2)
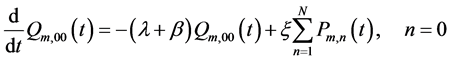 (3)
(3)
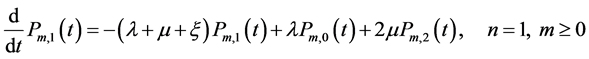 (4)
(4)
 (5)
(5)
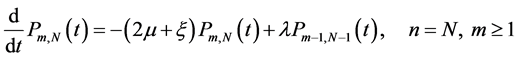 (6)
(6)
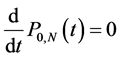 (7)
(7)
Taking Laplace transform of the Equations (2)-(6) w.r.t. t we have
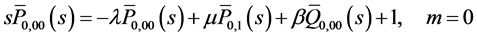 (8)
(8)






Since
where,
Define the probability generating functions by



Multiplying Equation (8) to (14) by





Multiplying Equation (18) to (21) by

The zeros of the denominator in (22) are given by

The existence of 




where
Now 



Applying the Leibniz differentiation theorem to (24), setting 



From (27), we have

where
We know that,
Using these identities in above equations, We are now in a position to complete the solution for the joint distribution of 

(30)

(32)

where,
4. Conclusion
This paper discussed the transient solution of M/M/2/N queuing system with catastrophic and restorations effects on the number of times system reached its capacity in time t. This model finds its application in computer- network communications, telecommunications etc.
Cite this paper
Dhanesh Garg, (2015) Transient Solution of M/M/2/N System Subjected to Catastrophe cum Restoration. Open Access Library Journal,02,1-8. doi: 10.4236/oalib.1101404
References
- 1. Chao, X. (1995) A Queuing Network Model with Catastrophes and Product form Solution. Operations Research Letters, 18, 75-79.
- 2. Kumar, B.K. and Arivudainambi, D. (2000) Transient Solution of an M/M/1 Queue with Catastrophes. Computers and Math with Applica, 40, 1233-1240.
- 3. Kumar, B.K. and Madheswari, S.P. (2002) Transient Behaviours of the M/M/2 Queue with Catastrophes. Statistica, Anno LXII, n1.
- 4. Di Crescenzo, A., Giorno, V. and Ricciardi, L.M. (2003) On the M/M/1 Queue with Catastrophes and Its Continuous Approximation. Queueing Systems, 43, 329-347.
- 5. Jain, N.K. and Kumar, R. (2007) Transient Solution of a Catastrophic-cum-Restorative Queueing Problem with Correlated Arrivals and Variable Service Capacity. Information and Management Sciences, 18, 461-465.
- 6. Jain, N.K. and Garg, D. (2011) Distribution of the Number of Times M/M/2/N Queuing System Reaches Its Capacity in Time t under Catastrophic Effects. International Journal of Computational Science and Mathematics, 3, 389-400.
- 7. Jain, N.K. and Garg, D. (2011) Distribution of the Number of Times M/M/2/N Queueing System with Heterogeneous Servers Reaches Its Capacity in Time t under Catastrophic Effects. International Journal of Computational and Applied Mathematics, 6, 169-192.
- 8. Garg, D. (2013) Distribution of the Number of Times M/M/2/N Queuing System with Heterogeneous Servers Reaches Its Capacity in Time t Subject to Catastrophes and Restorations. International Journal of Management Research and Development, 3, 31-61.
- 9. Garg, D. (2014) Approximate Analysis of an M/M/1 Markovian Queue Using Unit Step Function. Open Access Library Journal, 1, e973.
- 10. Garg, D. (2014) Two Server Queueing Systems Reaches Its Capacity in Time t. International Journal of Research in Advent Technology, 2, 417-421.
http://www.ijrat.org/downloads/may-2014/paper%20id-25201453.pdf - 11. Watson, G.N. (1959) A Treatise on the Theory of Bessel Function. 2nd Edition, Cambridge University Press, Cambridge.
- 12. Widder, D.V. (1946) The Laplace Transform. Princeton Mathematical Series.
- 13. Erdelyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F.G. (1954) Table of Integral Transform. Vol. 1, McGraw-Hill Book Company, New York.













