Received 24 March 2015; accepted 9 April 2015; published 13 April 2015

ABSTRACT

We will analyse perturbative quantum gravity on de Sitter spacetime. We propose a new type of inner product for modes on de Sitter spacetime. This inner product is used to mode decompose perturbations of the metric on de Sitter spacetime. Using this inner product, it is possible to calculate the two-point function for perturbative quantum gravity on de Sitter spacetime. This two- point function will be written in terms of a mode sum for various modes on de Sitter spacetime.

Keywords:

Perturbative Quantum Gravity, de Sitter Spacetime

Subject Areas: Applied Physics, Modern Physics

1. Introduction

Quantum field theory has been one of the greatest scientific achievements of the last centenary. The perturbative quantum theory has led to many important developments in high energy physics and condensed matter physics. These can include things like ghost condensation which causes the breaking of Lorentz symmetry [1] . It has also been used for analyzing the BRST and anti-BRST symmetries [2] . Most quantum field theories that are used in high energy physics are, gauge theories. Gravity can also be considered as a gauge theory of coordinate transformations [3] - [20] . As not all the degrees of freedom, in a theory with gauge symmetry are physical, so it such theories cannot be quantized without fixing a gauge. A gauge is fixed at the quantum level by adding a new term to the original action. This new term is called a gauge fixing term. However, apart from the gauge fixing term, we also need to add a ghost term to the original action. This ensures that the theory unitary to all orders in the perturbation theory. This term is called the ghost term. This term is composed of ghosts fields, which are not physical fields. But it is important to include these fields into the calculation to keep the theory unitarity [21] - [28] . Even though the perturbative quantum gravity is not renormalizable, it can be used in the framework of effective field theories. From an effective theory point of view there is no fundamental difference between renormalizable and non-renormalizable theories, except the way these theories depend on lower energy scale. The universe can be approximated by de Sitter spacetime in the inflationary era. The universe may also be approaching de Sitter spacetime asymptotically. So, we will study perturbative quantum gravity on de Sitter spacetime. Quantum field theory on has had some interesting applications [29] - [92] . The Hawking radiation was arrived at by studding quantum field theory in the back ground of a black hole. We will define an inner product for perturbative quantum gravity in de Sitter spacetime. The de Sitter spacetime is defined to be a spacetime of constant curvature. This curvature is always positive for de Sitter spacetime. This is because it is generated from a positive cosmological constant. This cosmological constant sets the rate of expansion of the universe.

2. de Sitter Spacetime

As this rate is measured by the Hubble’s constant H, so we can write

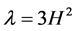(1)

The Hubble’s constant can be written in terms of the radius of de Sitter spacetime r,

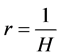(2)

Furthermore, we can write

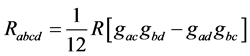(3)

So we get

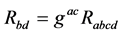(4)

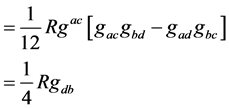(5)

Now we can also write

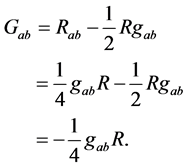(6)

As we know,

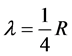(7)

So we can also write

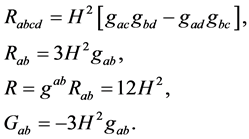(8)

The metric in de Sitter spacetime can be written as

(9)

Furthermore, we can write it using the metric on a three-sphere,

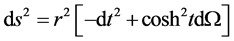(10)

Here 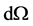is the metric on a three dimensional sphere,

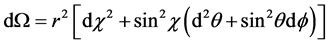(11)

Now using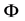, which is given by

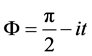(12)

we can write

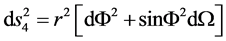(13)

3. Perturbative Quantum Gravity

We now start with pure gravity with a cosmological constant. The Lagrangian for pure gravity with a cosmological constant is

(14)

We adopt units, such that

(15)

We now split the metric into a background metric and small perturbations of of that metric. Then we treat the perturbation as a classical field and try to quantize it,

(16)

Now we have

(117)

and

(18)

If is the original Riemann tensor and is the background Riemann tensor then we have up to second order in,

(19)

where we have define

(20)

and

(21)

along with

(22)

We can now write,

(23)

So we have

(24)

This operator has a zero eigenvalue and it is not invertible. However, we can fix a gauge. This will be done by adding a ghost term and a gauge fixing term to the original action. Now if the sum of this term is given by, then we can define as the momentum current,

(25)

for perturbative quantum gravity are and. So, we can define as,

(26)

We have

(27)

Furthermore, the inner product on a space-like hyper-surface is gain by

(28)

Now we have

(29)

This inner product is conserved. Now by using a complete set of solutions and, we get

(30)

So we have

(31)

We also have

(32)

and

(33)

So, we can write

(34)

Now we can write

(35)

where

(36)

Thus we have

(37)

and

(38)

In Matrix notation, this can be written as

(39)

So we have

(40)

and

(41)

4. Conclusion

In this paper, we analysed the inner product for perturbative quantum gravity in de Sitter spacetime. In doing our calculations, we proposed a general kind of inner product for modes on de Sitter spacetime. Using this general inner product, we were able to calculate the two-point function on de Sitter spacetime. The de Sitter spacetime is important as the universe is expected to be approaching de Sitter spacetime. This two-point function can be written as a mode sum of the graviton modes on de Sitter spacetime. It may be noted that quantum gravity correction to quantum field theory has been studied [93] - [107] . It will be interesting to analyse such effects in de Sitter spacetime.

Cite this paper

Ashaq Hussain Sofi,Shabir Ahmad Akhoon,Asloob Ahmad Rather,Anil Maini, (2015) Perturbative Quantum Gravity on de Sitter Spacetime. Open Access Library Journal,02,1-9. doi: 10.4236/oalib.1101422

References