Open Access Library Journal
Vol.02 No.04(2015), Article ID:68288,8 pages
10.4236/oalib.1101421
Chern-Simons-Matter Theory in Superspace Formalism
Ashaq Hussain Sofi1, Sajad Ul Majeed2
1Department of Physics, National Institute of Technology, Srinagar, India
2Department of Physics, University of Kashmir, Srinagar, India
Email: shifs237@gmail.com, mohammadsajadullah99@gmail.com
Copyright © 2015 by authors and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 March 2015; accepted 9 April 2015; published 13 April 2015
ABSTRACT
In this letter, we will study the Chern-Simons-matter theory in Harmonic superspace. It will be shown that this superspace is well suited to write theories with high amount of supersymmetry. This will be done using harmonic variables. The harmonic superspace will have 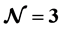 supersymmetry. It will be argued that it will be possible to analyse this theory in non-anticommutative superspace. The non-anticommutative superspace for this theory will be explicitly constructed.
supersymmetry. It will be argued that it will be possible to analyse this theory in non-anticommutative superspace. The non-anticommutative superspace for this theory will be explicitly constructed.
Keywords:
Chern-Simons-Matter Theory, Harmonic Superspace, Supersymmetry, Analytic Superspace
Subject Areas: Applied Physics, Modern Physics

1. Introduction
Harmonic superspace is well suited for analysing theories that have eight real generators of supersymmetry [1] . After complexification eight generators of supersymmetry correspond to the tensor product of a four dimensional Dirac spinors with the fundamental representation of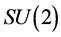 . The quotient space
. The quotient space 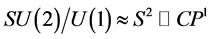 is a 2-sphere. This is because
is a 2-sphere. This is because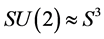 , and we get
, and we get 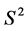 after a projection over
after a projection over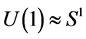 . Harmonic superspace describes theories with
. Harmonic superspace describes theories with 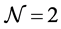 supersymmetry in four dimensions, in a manifestly covariant manner [2] - [4] . It also describes theories with
supersymmetry in four dimensions, in a manifestly covariant manner [2] - [4] . It also describes theories with 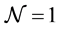 supersymmetry in five dimensions, in a manifestly covariant manner [5] - [8] . In three dimensions it can be used to describe theories with
supersymmetry in five dimensions, in a manifestly covariant manner [5] - [8] . In three dimensions it can be used to describe theories with 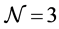 supersymmetry [9] [10] . If we view
supersymmetry [9] [10] . If we view 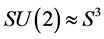 as a
as a 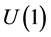 principle bundle over S2 with nonzero first Chern class, then the fields over S2 are characterized by an integral charge. Thus, harmonic variables,
principle bundle over S2 with nonzero first Chern class, then the fields over S2 are characterized by an integral charge. Thus, harmonic variables, 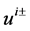 parameterizing the coset
parameterizing the coset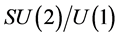 , satisfy the the following constraints
, satisfy the the following constraints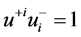 ,
,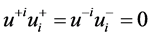 . Now the coordinates of harmonic superspace can be written as
. Now the coordinates of harmonic superspace can be written as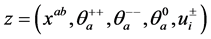 , where
, where 





where

We will now construct a harmonic superspace suitable for dealing with three dimensional theories. It will be shown that this harmonic superspace has 
2. Harmonic Superspace
We need to define harmonic superspace derivatives using harmonic variables, 


and

where the derivatives



They satisfy the following algebra

The conjugation in the harmonic superspace is defined by

The measure in full harmonic superspace is given by

and the measure in analytic superspace is given by

So, the analytic superspace measure is real 

3. Deformation
It is now possible to break a part of this supersymmetry by imposing the following anticommutation relationship,

where

Here this start product maps the non-anticommutative superspace to the usual harmonic superspace. This is a standard technique in non-anticommutativity and it is like the superspace version of Moylar star product. This will break a part of the supersymmetry of the theory. This could have been imposed by a background field, 


will modify the add the addition term to the star product by the inclusion of
from the previous factor. However, this new term does not break any supersymmetry.
We will study the Chern-Simons-matter theory in the harmonic superspace. Let the gauge fields corresponding to 


The action for the Chern-Simons-matter theory can now be written as

Not all the degrees of freedom of this theory are physical as it is invariant under gauge transformations [11]

4. Conclusion
We analysed a Chern-Simons theory in harmonic superspace. This superspace had 

Cite this paper
Ashaq Hussain Sofi,Sajad Ul Majeed, (2015) Chern-Simons-Matter Theory in Superspace Formalism. Open Access Library Journal,02,1-8. doi: 10.4236/oalib.1101421
References
- 1. Galperin, A.S., Ivanov, E.A., Ogievetsky, V.I. and Sokatchev, E.S. (2001) Harmonic Superspace. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9780511535109 - 2. Galperin, A., Ivanov, E., Ogievetsky, V. and Sokatchev, E. (1984) Harmonic Superspace: Key to N = 2 Supersymmetry Theories. JETP Letters, 40.
- 3. Zupnik, B.M. (1998) Supersymmetries and Quantum Symmetries. In: Wess, J. and Ivanov, E., Eds., Springer Lect. Notes in Phys, 524, 116.
- 4. Zupnik, B.M. and Hetselius, D.V. (1988) Three-Dimensional Extended Supersymmetry in Harmonic Superspace. Sov. J. Nucl. Phys. (Engl. Transl.) (United States), 47.
- 5. Kuzenko, S.M. and Linch III, W.D. (2006) On Five-Dimensional Superspaces. Journal of High Energy Physics, 2006, Article ID: 038.
http://dx.doi.org/10.1088/1126-6708/2006/02/038 - 6. Kuzenko, S.M. (2006) On Compactified Harmonic/Projective Superspace, 5D Superconformal Theories, and All That. Nuclear Physics B, 745, 176-207.
http://dx.doi.org/10.1016/j.nuclphysb.2006.03.019 - 7. Kuzenko, S.M. (2007) Five-Dimensional Supersymmetric Chern-Simons Action as a Hypermultiplet Quantum Correction. Physics Letters B, 644, 88-93.
http://dx.doi.org/10.1016/j.physletb.2006.11.035 - 8. Hatsuda, M. and Siegel, W. (2003) New Holographic Limit of AdS 5 S 5. Physical Review D, 67, Article ID: 066005.
http://dx.doi.org/10.1103/PhysRevD.67.066005 - 9. Ketov, S.V. (2000) Anomalous N = 2 Superconformal Ward Identities. Nuclear Physics B, 582, 119-138.
http://dx.doi.org/10.1016/S0550-3213(00)00266-2 - 10. Galperin, A., Ivanov, E., Kalitzin, S., Ogievetsky, V. and Sokatchev, E. (1984) Unconstrained N = 2 Matter, Yang-Mills and Supergravity Theories in Harmonic Superspace. Classical and Quantum Gravity, 1, 469.
http://dx.doi.org/10.1088/0264-9381/1/5/004 - 11. Buchbinder, I.L., Ivanov, E.A., Lechtenfeld, O., Pletnev, N.G., Samsonov, I.B. and Zupnik, B.M. (2009) ABJM Models in Script N = 3 Harmonic Superspace. Journal of High Energy Physics, 2009, 096.
http://dx.doi.org/10.1088/1126-6708/2009/03/096 - 12. Soloviev, M.A. (2013) Algebras with Convergent Star Products and Their Representations in Hilbert Spaces. Journal of Mathematical Physics, 54, Article ID: 073517.
http://dx.doi.org/10.1063/1.4815996 - 13. Soloviev, M.A. (2014) Wedge Locality and Asymptotic Commutativity. Physical Review D, 89, Article ID: 105020.
http://dx.doi.org/10.1103/PhysRevD.89.105020 - 14. Faizal, M. and Tsun, T.S. (2014) Monopoles in Superloop Space. EPL (Europhysics Letters), 107, Article ID: 20008.
http://dx.doi.org/10.1209/0295-5075/107/20008 - 15. You, Y. and Fradkin, E. (2013) Field Theory of Nematicity in the Spontaneous Quantum Anomalous Hall Effect. Physical Review B, 88, Article ID: 235124.
http://dx.doi.org/10.1103/PhysRevB.88.235124 - 16. Faizal, M. (2014) Multiverse in the Third Quantized Formalism. Communications in Theoretical Physics, 62, 697.
- 17. Piatek, M. (2014) Classical Torus Conformal Block, N = 2* Twisted Super-Potential and the Accessory Parameter of Lamé Equation. Journal of High Energy Physics, 2014, 124.
http://dx.doi.org/10.1007/JHEP03(2014)124 - 18. Faizal, M. and Kruglov, S.I. (2014) Deformation of the Dirac Equation. arXiv:1406.2653
- 19. Faizal, M. (2013) Chern-Simons-Matter Theory. International Journal of Modern Physics A, 28, Article ID: 1350012.
http://dx.doi.org/10.1142/S0217751X13500127 - 20. Faizal, M. (2013) Aspects of ABJ Theory. Journal of High Energy Physics, 2013, 156.
http://dx.doi.org/10.1007/JHEP01(2013)156 - 21. Papenbrock, T. and Weidenmüller, H.A. (2014) Effective Field Theory for Finite Systems with Spontaneously Broken Symmetry. Physical Review C, 89, Article ID: 014334.
http://dx.doi.org/10.1103/PhysRevC.89.014334 - 22. Stengel, M. (2013) Flexoelectricity from Density-Functional Perturbation Theory. Physical Review B, 88, Article ID: 174106.
http://dx.doi.org/10.1103/PhysRevB.88.174106 - 23. Faizal, M. and Upadhyay, S. (2014) Spontaneous Breaking of the BRST Symmetry in the ABJM Theory. Physics Letters B, 736, 288-292.
http://dx.doi.org/10.1016/j.physletb.2014.07.040 - 24. Faizal, M. Deformation of Second and Third Quantization. arXiv:1503.04797
- 25. Ali, A.F., Faizal, M. and Majumder, B. (2015) Absence of an Effective Horizon for Black Holes in Gravity’s Rainbow. EPL (Europhysics Letters), 109, Article ID: 20001.
http://dx.doi.org/10.1209/0295-5075/109/20001 - 26. Faizal, M. (2013) Superloop Space. EPL (Europhysics Letters), 103, Article ID: 21003.
http://dx.doi.org/10.1209/0295-5075/103/21003 - 27. Witten, E. (2012) Superstring Perturbation Theory Revisited. arXiv:1209.5461
- 28. Faizal, M. (2012) Some Aspects of Virtual Black Holes. Journal of Experimental and Theoretical Physics, 114, 400-405.
http://dx.doi.org/10.1134/S1063776112020045 - 29. Witten, E. (2000) Duality Relations among Topological Effects in String Theory. Journal of High Energy Physics, 2000, 031.
http://dx.doi.org/10.1088/1126-6708/2000/05/031 - 30. Faizal, M. (2011) BRST and Anti-BRST Symmetries in Perturbative Quantum Gravity. Foundations of Physics, 41, 270-277.
http://dx.doi.org/10.1007/s10701-010-9511-6 - 31. Witten, E. and Homology, K. (2011) Khovanov Homology and Gauge Theory. arXiv:1108.3103
- 32. Faizal, M. and Khan, M. (2011) A Superspace Formulation of the BV Action for Higher Derivative Theories. The European Physical Journal C-Particles and Fields, 71, 1-5.
http://dx.doi.org/10.1140/epjc/s10052-011-1603-8 - 33. Faizal, M. (2014) Deformation of the Wheeler-DeWitt Equation. International Journal of Modern Physics A, 29, Article ID: 1450106.
http://dx.doi.org/10.1142/S0217751X14501061 - 34. Witten, E. (2009) Branes, Instantons, and Taub-NUT Spaces. Journal of High Energy Physics, 2009, 067.
http://dx.doi.org/10.1088/1126-6708/2009/06/067 - 35. Witten, E. (2009) Geometric Langlands from Six Dimensions. arXiv:0905.2720
- 36. Faizal, M., Ali, A.F. and Nassar, A. (2014) AdS/CFT Correspondence beyond Its Supergravity Approximation.
arXiv:1405.4519 - 37. Witten, E. 2010) Analytic Continuation of Chern-Simons Theory. arXiv:1001.2933
- 38. Witten, E. (2008) The Problem of Gauge Theory. arXiv:0812.4512
- 39. Faizal, M. (2014) Consequences of Deformation of the Heisenberg Algebra. International Journal of Geometric Methods in Modern Physics, 12, Article ID: 1550022.
- 40. Zanon, D. (2001) Noncommutative Perturbation in Superspace. Physics Letters B, 504, 101-108.
http://dx.doi.org/10.1016/S0370-2693(01)00271-4 - 41. Faizal, M. and Tsun, T.S. (2015) Polyakov Loops for the ABJ Theory. International Journal of Theoretical Physics, 54, 896-909.
- 42. Terashima, S. and Yee, J.T. (2003) Comments on Noncommutative Super-Space. Journal of High Energy Physics, 2003, 053.
http://dx.doi.org/10.1088/1126-6708/2003/12/053 - 43. Setare, M.R. and Adami, H. The Entropy Formula of Black Holes in Minimal Massive Gravity and Its Application for BTZ Black Holes.
arxiv:1501.00920 - 44. Witten, E. (2008) Gauge Theory and Wild Ramification. Analysis and Applications, 6, 429-501.
http://dx.doi.org/10.1142/S0219530508001195 - 45. Faizal, M. (2013) Fourth Quantization. Physics Letters B, 727, 536-540.
http://dx.doi.org/10.1016/j.physletb.2013.10.069 - 46. Faizal, M. (2014) Noether’s Charge in the Super-Group Field Cosmology. Gravitation and Cosmology, 20, 132-137.
http://dx.doi.org/10.1134/S0202289314020030 - 47. Witten, E. (2007) Three-Dimensional Gravity Revisited. arXiv:0706.3359
- 48. Faizal, M. (2014) Boundary Effects in the BLG Theory. Modern Physics Letters A, 29, Article ID: 1450154.
http://dx.doi.org/10.1142/S0217732314501545 - 49. Berkovits, N. and Witten, E. (2004) Conformal Supergravity in Twistor-String Theory. Journal of High Energy Physics, 2004, 009.
http://dx.doi.org/10.1088/1126-6708/2004/08/009 - 50. Witten, E. (2004) Parity Invariance for String in Twistor Space. Advances in Theoretical and Mathematical Physics, 8, 799-796.
- 51. Witten, E. (2004) Perturbative Gauge Theory as a String Theory in Twistor Space. Communications in Mathematical Physics, 252, 189-258.
http://dx.doi.org/10.1007/s00220-004-1187-3 - 52. Seiberg, N. (2003) Noncommutative Superspace, Script N = 1/2 Supersymmetry, Field Theory and String Theory. Journal of High Energy Physics, 2003, 010.
http://dx.doi.org/10.1088/1126-6708/2003/06/010 - 53. Faizal, M. (2011) Spontaneous Breaking of Lorentz Symmetry by Ghost Condensation in Perturbative Quantum Gravity. Journal of Physics A: Mathematical and Theoretical, 44, Article ID: 402001.
http://dx.doi.org/10.1088/1751-8113/44/40/402001 - 54. Faizal, M. (2011) Perturbative Quantum Gravity on Complex Space-Time. Physics Letters B, 705, 120-123.
http://dx.doi.org/10.1016/j.physletb.2011.09.062 - 55. Beasley, C. and Witten, E. (2003) Residues and World-Sheet Instantons. Journal of High Energy Physics, 2003, 065.
http://dx.doi.org/10.1088/1126-6708/2003/10/065 - 56. Pourhassan, B. and Faizal, M. Thermal Fluctuations in a Charged AdS Black Hole. arXiv:1503.07418
- 57. Faizal, M. (2011) M Theory on Deformed Superspace. Physical Review D, 84, Article ID: 106011.
http://dx.doi.org/10.1103/PhysRevD.84.106011 - 58. Klebanov, I.R. and Witten, E. (2003) Proton Decay in Intersecting D-Brane Models. Nuclear Physics B, 664, 3-20.
http://dx.doi.org/10.1016/S0550-3213(03)00410-3 - 59. Cachazo, F., Seiberg, N. and Witten, E. (2003) Chiral Rings and Phases of Supersymmetric Gauge Theories. Journal of High Energy Physics, 2003, 018.
http://dx.doi.org/10.1088/1126-6708/2003/04/018 - 60. Faizal, M. (2012) Covariant Graviton Propagator in Anti-De Sitter Spacetime. Classical and Quantum Gravity, 29, Article ID: 035007.
http://dx.doi.org/10.1088/0264-9381/29/3/035007 - 61. Faizal, M. (2012) Multiverse in the Third Quantized Horava-Lifshitz Theory of Gravity. Modern Physics Letters A, 27, Article ID: 1250007.
http://dx.doi.org/10.1142/S0217732312500071 - 62. Witten, E. (2003) Chiral Ring of Sp(N) and SO(N) Supersymmetric Gauge Theory in Four Dimensions. Chinese Annals of Mathematics, 24, 403.
http://dx.doi.org/10.1142/S0252959903000402 - 63. Faizal, M. (2013) Noncommutative Quantum Gravity. Modern Physics Letters A, 28, Article ID: 1350034.
http://dx.doi.org/10.1142/S021773231350034X - 64. Witten, E. (2002) Singularities in String Theory. Proceedings of the ICM, Vol. 1, Beijing, 2002, 495-504.
- 65. Witten, E. (2002) Comments on String Theory. arXiv:hepth/0212247
- 66. Faizal, M. and Smith, D.J. (2012) Supersymmetric Chern-Simons Theory in the Presence of a Boundary. Physical Review D, 85, Article ID: 105007.
http://dx.doi.org/10.1103/PhysRevD.85.105007 - 67. Faizal, M. (2012) Noncommutativity and Non-Anticommutativity Perturbative Quantum Gravity. Modern Physics Letters A, 27, Article ID: 1250075.
http://dx.doi.org/10.1142/S0217732312500757 - 68. Friedmann, T. and Witten, E. (2003) Unification Scale, Proton Decay, and Manifolds of G2 Holonomy. Advances in Theoretical and Mathematical Physics, 7, 577-617.
http://dx.doi.org/10.4310/ATMP.2003.v7.n4.a1 - 69. Mir, F. (2012) M-Theory in the Gaugeon Formalism. Communications in Theoretical Physics, 57, 637-640.
http://dx.doi.org/10.1088/0253-6102/57/4/20 - 70. Witten, E. (2002) Quest for Unification. arXiv:hep-ph/0207124
- 71. Witten, E. (2002) Deconstruction, G2 Holonomy, and Doublet-Triplet Splitting. arXiv:hep-ph/0201018
- 72. Faizal, M. (2012) Gauge and Supersymmetric Invariance of a Boundary Bagger-Lambert-Gustavsson Theory. Journal of High Energy Physics, 2012, 17.
http://dx.doi.org/10.1007/JHEP04(2012)017 - 73. Witten, E. (2001) Multi-Trace Operators, Boundary Conditions, and AdS/CFT Correspondence.
arXiv:hep-th/0112258 - 74. Faizal, M. (2012) Deformation of the ABJM Theory. EPL (Europhysics Letters), 98, Article ID: 31003.
http://dx.doi.org/10.1209/0295-5075/98/31003 - 75. Faizal, M. (2012) Harmonic Superspace Gaugeon Formalism for the ABJM Theory. Modern Physics Letters A, 27, Article ID: 1250147.
http://dx.doi.org/10.1142/S0217732312501477 - 76. Faizal, M. (2012) The BV Formalization of Chern-Simons Theory on Deformed Superspace. Communications in Theoretical Physics, 58, 704.
http://dx.doi.org/10.1088/0253-6102/58/5/14 - 77. Ferrara, S., Lledó, M.A. and Maciá, O. (2003) Supersymmetry in Noncom-Mutative Superspaces. Journal of High Energy Physics, 2003, 068.
http://dx.doi.org/10.1088/1126-6708/2003/09/068 - 78. Faizal, M. (2014) Absence of Black Holes Information Paradox in Group Field Cosmology. International Journal of Geometric Methods in Modern Physics, 11, Article ID: 1450010.
http://dx.doi.org/10.1142/S0219887814500108 - 79. Nazaryan, V. and Carlson, C.E. (2005) Field Theory in Noncommutative Minkowski Superspace. Physical Review D, 71, Article ID: 025019.
http://dx.doi.org/10.1103/PhysRevD.71.025019 - 80. Nazaryan, V. and Carlson, C.E. (2005) A Field Theoretical Model in Noncommutative Minkowski Superspace. International Journal of Modern Physics A, 20, 3495-3501.
http://dx.doi.org/10.1142/S0217751X05026820 - 81. Faizal, M. (2012) Super-Group Field Cosmology. Classical and Quantum Gravity, 29, Article ID: 215009.
http://dx.doi.org/10.1088/0264-9381/29/21/215009 - 82. Sepehri, A., Faizal, M., Setare, M.R. and Ali, A.F. (2015) Holographic Cosmology from BIonic Solutions.
arXiv:1502.05218 - 83. Witten, E. (2001) Overview of K-Theory Applied to Strings. International Journal of Modern Physics A, 16, 693-706.
http://dx.doi.org/10.1142/S0217751X01003822 - 84. Witten, E. (2001) Lepton Number and Neutrino Masses. Nuclear Physics B-Proceedings Supplements, 91, 3-8.
http://dx.doi.org/10.1016/S0920-5632(00)00916-6 - 85. Faizal, M. (2013) Deformed Super-Yang-Mills in Batalin-Vilkovisky Formalism. International Journal of Theoretical Physics, 52, 392-403.
http://dx.doi.org/10.1007/s10773-012-1344-y - 86. Faizal, M. and Smith, D.J. (2013) Nonanticommutativity in the Presence of a Boundary. Physical Review D, 87, Article ID: 025019.
http://dx.doi.org/10.1103/PhysRevD.87.025019 - 87. Kobayashi, Y. and Sasaki, S. (2005) Nonlocal Wess-Zumino Model on Nilpotent Noncommutative Superspace. Physical Review D, 72, Article ID: 065015.
http://dx.doi.org/10.1103/PhysRevD.72.065015 - 88. Faizal, M., Mandal, B.P. and Upadhyay, S. (2013) Finite BRST Transformations for the Bagger-Lambert-Gustavsson Theory. Physics Letters B, 721, 159-163.
http://dx.doi.org/10.1016/j.physletb.2013.02.057 - 89. Kruglov, S.I. and Faizal, M. (2014) Wave Function of the Universe from a Matrix Valued First-Order Formalism.
arXiv:1408.3794 - 90. Garattini, R. and Majumder, B. (2014) Naked Singularities Are Not Singular in Distorted Gravity. Nuclear Physics B, 884, 125-141.
http://dx.doi.org/10.1016/j.nuclphysb.2014.04.014 - 91. Awad, A., Ali, A.F. and Majumder, B. (2013) Nonsingular Rainbow Universes. Journal of Cosmology and Astroparticle Physics, 2013, 052.
http://dx.doi.org/10.1088/1475-7516/2013/10/052 - 92. Awad, A. and Ali, A.F. (2014) Minimal Length, Friedmann Equations and Maximum Density. Journal of High Energy Physics, 2014, 93.
http://dx.doi.org/10.1007/JHEP06(2014)093 - 93. Witten, E. (2000) Supersymmetric index in Four-Dimensional Gauge Theories. Advances in Theoretical and Mathematical Physics, 5, 841-907.
- 94. Dolan, L. and Witten, E. (1999) Vertex Operators for AdS3 Background with Ramond Ramond flux. Journal of High Energy Physics, 1999, 003.
http://dx.doi.org/10.1088/1126-6708/1999/11/003 - 95. Faizal, M. (2013) Non-Anticommutative ABJ Theory. Nuclear Physics B, 869, 598-607.
http://dx.doi.org/10.1016/j.nuclphysb.2012.12.018 - 96. Faizal, M. Deformation of Second and Third Quantization. arXiv:1503.04797
- 97. Cook, J.S. (2006) Gauged Wess-Zumino Model in Noncommutative Minkowski Superspace. Journal of Mathematical Physics, 47, Article ID: 012304.
http://dx.doi.org/10.1063/1.2162330 - 98. Chang-Young, E., Kim, H. and Nakajima, H. (2008) Noncommutative Superspace and Super Heisenberg Group. Journal of High Energy Physics, 2008, 004.
http://dx.doi.org/10.1088/1126-6708/2008/04/004 - 99. Faizal, M. and Awad, A. (2015) Four Dimensional Supersymmetric Theories in Presence of a Boundary.
arXiv:1502.07717 - 100. Das, S., Robbins, M.P. and Walton, M.A. (2014) Generalized Uncertainty Principle Corrections to the Simple Harmonic Oscillator in Phase Space. arXiv:1412.6467
- 101. Balasubramanian, V., Das, S. and Vagenas, E.C. (2014) Generalized Uncertainty Principle and Self-Adjoint Operators.
arXiv:1404.3962 - 102. Garattini, R. Vacuum Energy Estimates in Quantum Gravity and the Wheeler-DeWitt Equation. arXiv:gr-qc/9604004
- 103. Majumder, B. (2013) Quantum Rainbow Cosmological Model with Perfect Fluid. International Journal of Modern Physics D, 22, Article ID: 1350079.
http://dx.doi.org/10.1142/S021827181350079X - 104. Faizal, M., Khalil, M.M. and Das, S. (2014) Time Crystals from Minimum Time Uncertainty. arXiv:1501.03111
- 105. Gangopadhyay, S., Dutta, A. and Faizal, M. (2015) Constraints on the Generalized Uncertainty Principle from Black Hole Thermodynamics. arXiv:1501.01482
- 106. Faizal, M. and Tsun, T.S. (2014) Supersymmetric Duality in Superloop Space. arXiv:1412.7594
- 107. Faizal, M., Ali, A.F. and Das, S. (2014) Discreteness of Time in the Evolution of the Universe. arXiv:1411.5675
- 108. Pramanik, S., Faizal, M., Moussa, M. and Ali, A.F. (2014) The Path Integral Quantization Corresponding to the Deformed Heisenberg Algebra. arXiv:1411.4979
- 109. Faizal, M. and Khalil, M.M. (2014) GUP-Corrected Thermodynamics for All Black Objects and the Existence of Remnants. arXiv:1411.4042
- 110. Ali, A.F., Faizal, M. and Khalil, M.M. (2014) Absence of Black Holes at LHC Due to Gravity’s Rainbow.
arXiv:1410.4765 - 111. Ali, A.F., Faizal, M. and Khalil, M.M. (2014) Remnants of Black Rings from Gravity’s Rainbow. Journal of High Energy Physics, 2014, 159.
http://dx.doi.org/10.1007/JHEP12(2014)159 - 112. Ali, A.F., Faizal, M. and Khalil, M.M. (2014) Remnant for All Black Objects Due to Gravity’s Rainbow.
arXiv:1410.5706 - 113. Majumder, B. and Sen, S. (2012) Do the Modified Uncertainty Principle and Polymer Quantization Predict Same Physics? Physics Letters B, 717, 291-294.
http://dx.doi.org/10.1016/j.physletb.2012.09.035

