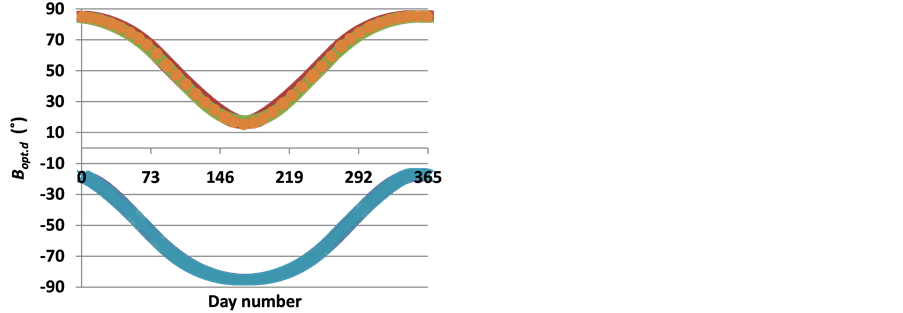Open Access Library Journal
Vol.03 No.02(2016), Article ID:68262,11 pages
10.4236/oalib.1102385
Solar Receivers Optimum Tilt Angle at Southern Hemisphere
Soulayman Soulayman1, Alhelou Mohammad2, Nouredine Salah3
1Department of Applied Physics, Higher Institute for Applied Sciences and Technology, Damascus, Syria
2Department of Electromechanical Systems, Higher Institute for Applied Sciences and Technology, Damascus, Syria
3Al-Andalus University for Medical Sciences, Qadmus, Syria

Copyright © 2016 by authors and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 9 February 2016; accepted 24 February 2016; published 29 February 2016

ABSTRACT
One of the important parameters that affects the performance of a solar collector is its tilt angle with the horizon. This is because the variation of tilt angle changes the amount of solar radiation reaching the collector surface. Meanwhile, is the rule of thumb, which says that solar collector should be orientated towards the Equator with a tilt equal to latitude, valid for high latitudes region? Thus, it is required to determine the optimum tilt for Equator facing collectors. In addition, the question may rise: how much adjustments of Equator facing solar collector tilt angle is reasonable to do during a year? A mathematical model was used for estimating the solar radiation on a tilted surface, and to determine the optimum tilt angle and orientation (surface azimuth angle) for the solar collector at any latitude. This model was applied for determining optimum tilt angle in the high latitudes zone in the Southern Hemisphere, on a daily basis, as well as for a specific period. The optimum angle was computed by searching for the values for which the radiation on the collector surface is a maximum for a particular day or a specific period. The results reveal that changing the tilt angle 12 times in a year (i.e. using the monthly optimum tilt angle) maintains approximately the total amount of solar radiation near the maximum value that is found by changing the tilt angle daily to its optimum value. This achieves a yearly gain in solar radiation up to 1.8 times of the case of a horizontal surface while the daily gain reaches 60 times approximately. Moreover, general formulas are proposed for predicting daily optimum tilt angle and optimum tilt angle over any number of days.
Keywords:
Southern Hemisphere, Optimum Tilt, Energy Gain, High Latitudes
Subject Areas: Environmental Sciences

1. Introduction
The performance of a solar collector is highly influenced by its orientation (with respect to the Equator) and its angle of tilt with the horizon (with respect to the ground). This is due to the fact that both the orientation and tilt angle change the solar radiation reaching the surface of the collector. Designing an installation to yield maximum annual energy minimizes the necessary installed capacity and reduces the cost of equipment. To achieve this, solar collector must be mounted at right angles to the Sun’s rays. The best way to collect maximum daily energy is to use tracking systems. A tracker is a mechanical device that follows the direction of the Sun on its daily sweep across the sky. The most effective tracking could be achieved by mounting the collector on a two-axis tracker that continuously tracks the Sun by the hour and through the seasons. As the trackers are expensive, and need energy for their operation, this method of tracking is quite cumbersome and inconvenient practically. Thus, the majority of installations are with fixed mountings. Therefore, it is often practicable to orient the solar collector at an optimum tilt angle, Bopt and to correct the tilt from time to time. For this purpose, one should be able to determine the optimum slope of the collector at any latitude, for any surface azimuth angle, and on any day or any period of the year. Various schemes have been proposed for optimizing the tilt angle and orientation of solar collectors designed for different geographical latitudes or possible utilization periods. However, as the goal of this work is to treat this question regarding the high latitudes region in Southern Hemisphere, it is reasonable to restrict ourselves to main available literature concerning this zone directly or indirectly.
In this context, Soulayman [1] proposed a general algorithm for calculating Bopt for south facing collector at any latitude from 0˚ to 60˚. Soulayman and Sabbagh [2] proposed an algorithm for determining Bopt at any latitude, L, and for any direction (surface azimuth angle, G). This algorithm could be used for treating Bopt in the high latitudes regions. Stanciu, and Stanciu [3] proposed a simple formula for determining the optimum tilt of south facing collector at latitudes from 0˚ to 80˚. Nijegorodov et al. [4] presented 12 equations (one for each month), for determining optimum tilt angle for any location that lies between latitude 60˚ south to 60˚ north. Mujahid [5] computed the optimum slope angle for latitude of 10˚ north to 50˚ north and concluded that if the collector adjusted by the seasonally optimum angles, 10% more energy is received compared with the zero slope angle. Calabrò [6] proposed an algorithm to calculate the optimum tilt angle of solar panels by means of global horizontal solar radiation data, provided from Earth-based meteorological stations. This mathematical modeling is based on the maximization of the theoretical expression of the global solar irradiation impinging on an inclined surface, with respect to the slope and orientation of the panel and to the solar hour angle. A set of transcendent equations resulted, whose solutions give the optimum tilt and orientation of a solar panel. A simulation was carried out using global horizontal solar radiation data from the European Solar Radiation Atlas and some empirical models of diffuse solar radiation. The optimum tilt angle resulted was related to latitude by a linear regression. The standard error of the mean values resulted increased significantly with latitude, suggesting that unreliable values can be provided at high latitudes. So, in the previous studies, no definite value or relation is accepted by all researchers for the optimum tilt angle. Therefore, several attempts were made to determine, or at least to estimate, optimum tilt angle Bopt theoretically and experimentally.
The main objective of this study is to develop a simple and easy way for finding daily, monthly, seasonally, half-yearly and fixed optimum tilt angles for any location in the high latitudes regions and to determine the yearly energy gain. As experimental data concerning the treated question in the studied region are not available to authors, the results of the present study could not be compared with the experimental results. However, the comparison with theoretical results of other researchers will be provided.
2. Main Formulae
Radiation data are the best source of information for estimating average incidence radiation. Lacking these data, it is possible to use empirical relationships to estimate radiation from hours of sunshine or cloudiness, relative humidity and ambiance temperature, which are widely available from many hundreds of stations in many countries. The main part of empirical relationships is restricted to hours of sunshine or cloudiness. However, these relationships could be written as:
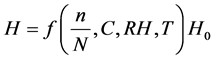 (1)
(1)
where H = monthly average daily radiation on a horizontal surface, H0 = the monthly average daily extraterrestrial solar radiation on a horizontal surface, n = monthly average daily hours of bright sunshine, N = monthly average of the maximum possible daily hours of bright sunshine (i.e., the day length of the average day of the month), C = monthly average daily cloud cover, RH = relative humidity and T = ambiance temperature. Supposing Equation (1) is applicable for daily values, it is to demonstrate that daily optimum tilt angle, Bopt,d is the solution of the following nonlinear algebraic equation:
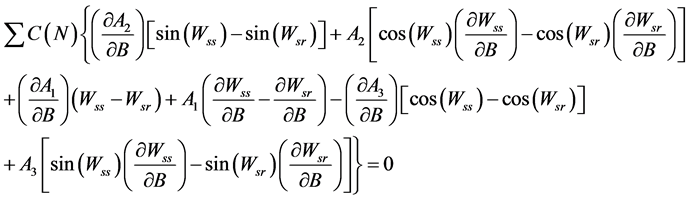 (2)
(2)
in relation to B where the summation should be ignored when dealing with daily period. In Equation (2) Wss and Wsr are the sunset and sunrise hour angle on tilted surface:
 (3)
(3)
 (4)
(4)
C(N) is the daily correction factor for Sun-Earth average distance:
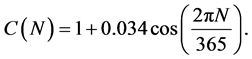 (5)
(5)
δ is the solar declination angle which could be calculated as below:
 (6)
(6)
A1, A2, A3 and A4 are functions of solar and collector angles:
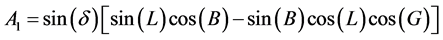 (7)
(7)
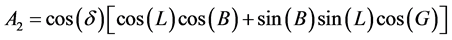 (8)
(8)
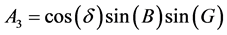 (9)
(9)
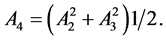 (10)
(10)
The geometric tilt factor Rb, the ratio of beam radiation on the optimum tilted surface to that on a horizontal surface at any time or period of time, can be calculated exactly in the case of extraterrestrial radiation by appropriate use of solar incidence angle on tilted surface and on horizon. A similar factor, Rb, could be introduced to express the solar energy gain on the optimum tilted surface to that tilted at angle equal to the latitude. For B = 0˚, B = Bopt, B = L daily extraterrestrial solar radiation is:
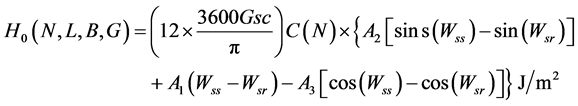 (11)
(11)
and summation by N should cover the length of period in consideration. For daily values no summation by N is used.
3. Results and Discussions
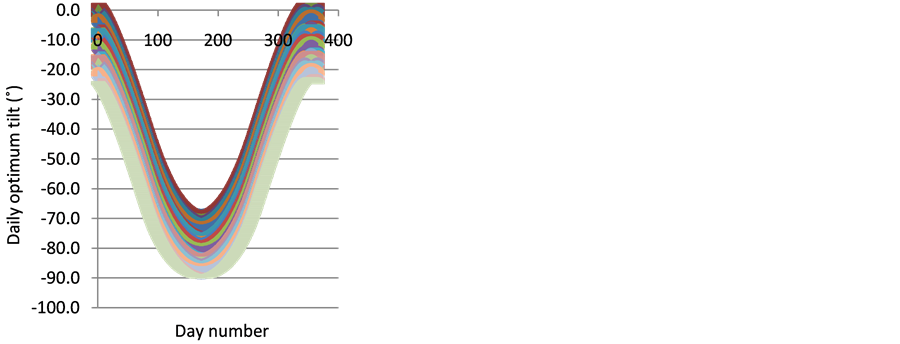
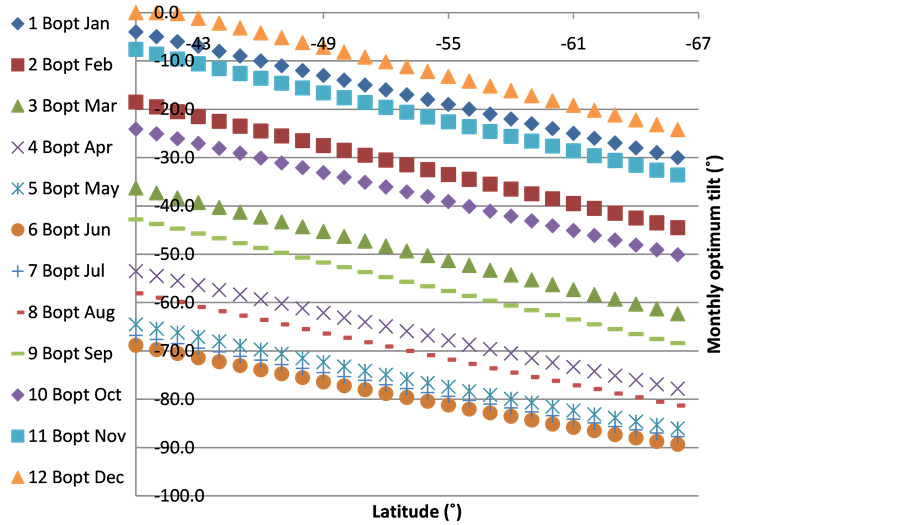
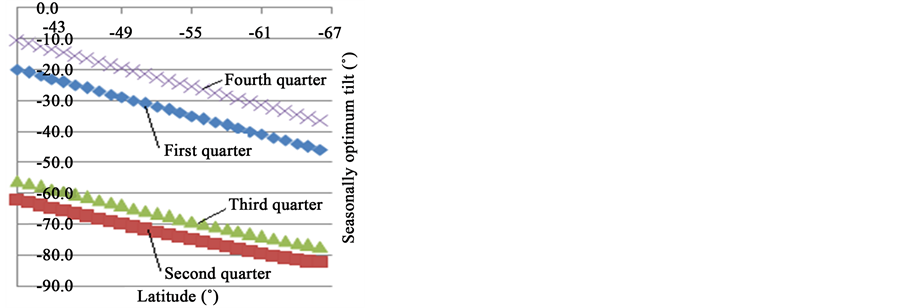
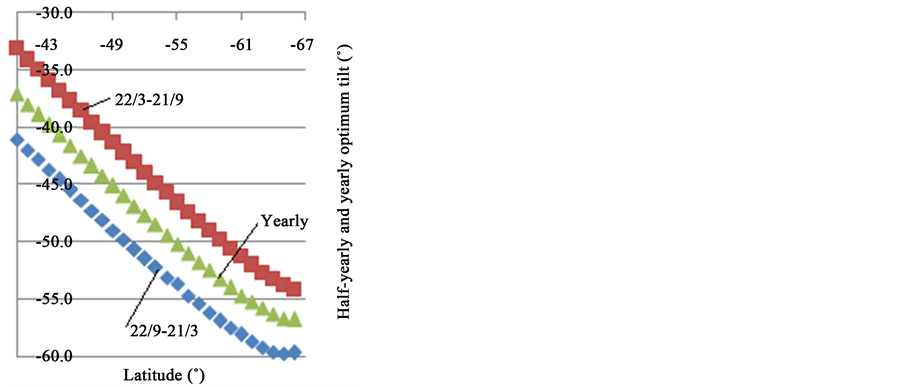
Soulayman [7] found that for latitudes which in absolute value are greater than 23.5˚ (outside of tropical region) the best orientation of the solar collector is Equator facing case (G = 0˚). Therefore, as the studied region is laid between 40˚S and 66˚S, the calculated results will be restricted to this case. Moreover, as the formula Bopt,d = L − δ proposed in [3] is a coarse approximation as proven in [7] , the comparison of the results of this work with those of [3] is meaningless. When solving Equation (2) for obtaining daily optimum tilt angle Bopt,d at latitudes from −40˚ to −66˚ the results presented in Figure 1 are obtained where the lower curve corresponds to −66˚ latitude and the upper curve corresponds to −40˚ latitude. It is seen from these results that collector orientation adjustment during the period started from 22/3 to 21/9 is more essential than during the other half-year. A similar result is obtained when solving Equation (2) for obtaining weekly optimum tilt angle Bopt,w, monthly tilt angle Bopt,m (see Figure 2), seasonally tilt angle Bopt,s (see Figure 3) and half-yearly (see Figure 4) at latitudes from −40˚ to −66˚. It is easy to conclude from Figure 1 that solar collector tilt adjustment is essential during the period started from 22/3 to 21/9 inclusively. Here it should be mentioned that, when comparing the results of this
Figure 1. Daily optimum tilt angle for latitudes [−40˚, −66˚] from up to down respectively.
Figure 2. Monthly optimum tilt angle for latitudes [−40˚, −66˚].
Figure 3. Seasonally optimum tilt angle for latitudes [−40˚, −66˚].
Figure 4. Half-yearly and yearly optimum tilt angle for latitudes [−40˚, −66˚].
work, concerning monthly optimum tilt angle at different latitudes, with those of [4] set of equations, it was observed that the results of [4] are in a good agreement with those of this work. However, the equations of [4] give a little bit higher values of optimum angle for the months of April, May, and August as compared with those obtained in this work while the agreement for other months is very good. Therefore, it should be noted that, the equations used in this work, as well as those used in [4] , were optimized using mathematical techniques without taking into account the localized patterns of solar radiation falling over a particular location (region). So, one or more assumptions of [4] are responsible for this disagreement.
Nijegorodov et al. [4] used mathematical models for calculating the hourly total radiation and then integrated them to obtain the total daily solar radiation. The main assumption of [4] is the clearness index is constant and equal to 0.7. As the clearness index is not generally constant and varies for each area between two values the slight difference could be because of this assumption.
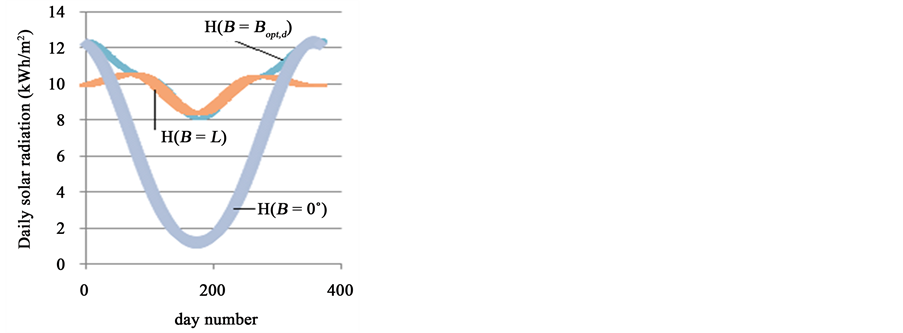
On the other hand, in order to evaluate the possible solar energy gain using tilt angle adjustment the total yearly extraterrestrial solar radiation at B = 0˚, B = Bopt, B = L should be calculated on a daily, monthly, seasonally as well as on a half-yearly and yearly basis. The results, for one example L = 55˚, are given on Figure 5 where H2 stands for solar radiation at B = Bopt, H1 stands for solar radiation at B = L and H0 stands for solar radiation at B = 0˚. It is seen from Figure 5 that solar radiation incident on a surface with optimum tilt angle has the maximum values all over the year. When comparing H2 with H1 it is seen from Figure 5 that H2 is greater than H1 remarkably over the period started from 22/9 to 21/3 while these values are near to each other during half a year started from 22/3 to 21/9.
By taking the ratio between the values related to surface with optimum tilt to those on a horizontal one and to
Figure 5. Daily extraterrestrial solar radiation received by a surface of different slopes at −55˚ latitude.
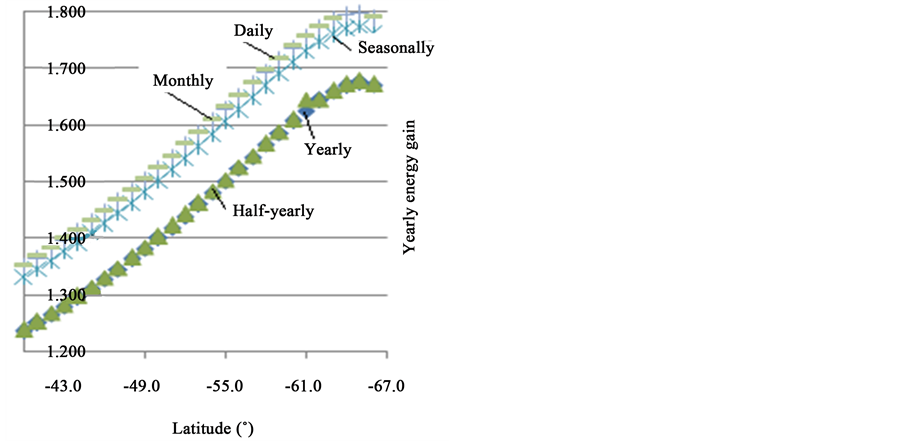
those tilted by latitude angle for the same period of time, the corresponded tilt factors, Rb = H2/H0 and Rb1 = H2/H1, could be calculated on daily, monthly, seasonally, half-yearly and yearly basis’s. These results are given in Figures 6-8.
It is seen from Figure 7 that solar collector tilt adjustment is essential during the period started from 22/3 to 21/9 where the daily solar energy gain can arrive about 60 times of solar radiation on horizontal plane while this gain is less than 2 times of solar radiation on horizontal plane during the period started from 22/9 to 21/3. Figures 6-8 show that the daily solar energy gain can arrive 1.3 times of solar radiation on latitude tilted plane during the period started from 22/9 to 21/3 while this gain is less than 1.15 times of solar radiation on latitude tilted plane during the period started from 22/3 to 21/9.
4. General Formulae for Determining Optimum Tilt Angles
When applying the algorithms proposed in [8] and [9] on the high latitude zones at Southern Hemisphere and analyzing the obtained results for each latitude as a function of δ, the following results were found.
4.1. Daily Tilt Angle
It was found that daily optimum tilt angle, Bopt,d, can be calculated effectively using the following equation:
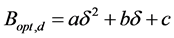
where “a”, “b” and “c” are functions of latitude L. These functions are of the following form:

El-Kassa by [10] proposed a formula for determining Bopt,d at latitudes up to 60˚ in Northern Hemisphere with verifying the applicability of his formula during the period starting from 22/9 to 21/3 but his formula suffers from uncertainty during period starting from 22/3 to 21/9 (see [1] for more details). Skeiker [11] presented his study aiming to develop an analytical procedure to obtain formula for determining Bopt,d for any chosen day at any latitude in Northern Hemisphere but he repeated the same formula of El-Kassaby [10] (see [2] for more details). So, no need to compare the results of the present work with those of [10] and [11] . Figure 9 shows the results of applying Equation (2) and Equation (12) for determining Bopt,d for 60˚S latitudes and Equation (2), the algorithm of [8] in addition to results of [1] for 60˚N. It is seen from Figure 9 that the results of the present work agree very well with those of [1] and the algorithm of [8] . Moreover, Equation (12) gives an excellent fit of the calculated results of the algorithm in this work.
When applying Equation (12), that of [3] , and the algorithm of [8] in calculating Bopt,d for L = −50˚ the
Figure 6. Yearly solar energy gain calculated basing on daily, monthly, seasonally, half-yearly and yearly optimum tilt angle for latitudes [−40˚, −66˚].
Figure 7. Daily solar energy gain in relation to horizontal surface for latitude −65˚.
Figure 8. Daily solar energy gain in relation to latitude tilted surface for latitude −65˚.
Figure 9. Daily optimum tilt angle for latitudes −60˚ (60S in SH) lower curve and 60˚ (60N in NH).
obtained results are given in Table 1. It is seen from Table 1 that regarding to the precise results of algorithm [8] , a) For Southern Hemisphere, the equation in [3] underestimates Bopt,d remarkably during the period starting from 22/9 to 21/3 and overestimates slightly Bopt,d during the period starting from 22/3 to 21/9 with an absolute deviation < 5˚; and b) Equation (12) gives the results of the algorithm with an absolute deviation < 1˚; So Equation (12) could be applied with a very good accuracy with regard to the algorithm [8] while the equation in [3] gives an acceptable evaluation of daily optimum tilt angle during half a year only.
4.2. Monthly Tilt Angle
When integrating Equation (12) for obtaining optimum tilt angle Bopt,p at any period of time one obtains the following formula:
where N1 and N2 are the day numbers of the period beginning and ending respectively.
When calculating monthly optimum tilt angle 60˚S latitude using Equation (16) and comparing the obtained results with those of set of equations in [4] and set of equations in [12] with taking into consideration the latitudes interval of the applicability of the mentioned references it was observed that in the Southern Hemisphere the results of the present work are in a very good agreement with those of [4] , and [12] (see Table 2). However, the equations of [4] give a little bit higher values of optimum angle for the months of April, May, and August as compared with those of [12] and present work while the agreement for other months is very good.
It could be noted that, the methodologies used in [4] [12] and present work are based on the optimization using mathematical techniques without taking into account the localized patterns of solar radiation falling over a particular location (region). So, one or more assumptions of [4] are responsible for this little disagreement. Nijegorodov et al. [4] used mathematical models for calculating the hourly total radiation and then integrated them to obtain the total daily solar radiation. The main assumption of [4] is the clearness index is constant and equal to 0.7. As the clearness index is not generally constant and varies for each area between two values the slight difference could be because of this assumption.
Statistical indicators used in Table 2 are:
a) The mean bias error (MBE) given by:
Table 1. A comparison between different approaches in calculating daily optimum tilt angle.
Table 2. A comparison between different approaches in calculating monthly optimum tilt angle.
b) The root mean square error (RMSE) given by:
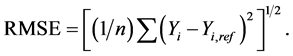
c) The t-statistic is given as:

n is the number of data pairs; 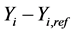
5. Conclusions
A mathematical model was applied for determining the optimum tilt angle of the solar collector at any latitude of the interval [−40˚, −66˚] in Southern Hemisphere. The optimum tilt angle was computed by searching for the values for which the radiation on the collector surface is a maximum for a particular day or a specific period. For an equator facing flat solar collector:
It is sufficient to adjust solar collectors tilt angle weekly (once/week) as this adjustment leads to the daily gain approximately.
It is sufficient to adjust solar collectors tilt angle 12 times (once/month) as this adjustment leads to the daily gain approximately.
It is practically sufficient to adjust solar collectors tilt angle twice a year: once from 22/3 to 21/9 and the other from 22/9 to 21/3 as the losses in the energy gain are not very important.
It is practically sufficient to orientate the solar collectors at tilt angle equal to the latitudes during the period started from 22/3 to 21/9 as the losses in the energy gain are less than 0.2.
The first part of the rule of thumb, which says that solar collector should be orientated towards the Equator is true for high latitudes in Southern Hemisphere while the second part, which says that solar collectors should be tilted at angle equal to latitude, is not valid during the started from 22/9 to 21/3 for high latitudes region.
General formulae were proposed for determining optimum daily tilt angle and optimum tilt angle for any number of days.
The applicability of the proposed formulae was verified.
This study will be hopefully expanded to cover northern high latitudes zone.
Acknowledgements
Authors thank Dr. R. Jabra for useful discussions and English reviewing.
Cite this paper
Soulayman Soulayman,Alhelou Mohammad,Nouredine Salah, (2016) Solar Receivers Optimum Tilt Angle at Southern Hemisphere. Open Access Library Journal,03,1-11. doi: 10.4236/oalib.1102385
References
- 1. Soulayman, S. (1991) On the Optimum Tilt of Solar Absorber Plates. Renewable Energy, 1, 551-554.
http://dx.doi.org/10.1016/0960-1481(91)90070-6 - 2. Soulayman, S. and Sabbagh, W. (2015) Comment on “Optimum Tilt Angle and Orientation for Solar Collectors in Syria” by Skeiker, K. Energy Conversion and Management, 89, 1001-1002.
http://dx.doi.org/10.1016/j.enconman.2014.10.023 - 3. Stanciu, C. and Stanciu, D. (2014) Optimum Tilt Angle for Flat Plate Collectors All over the World—A Declination Dependence Formula and Comparisons of Three Solar Radiation Models. Energy Conversion and Management, 81, 133-143.
http://dx.doi.org/10.1016/j.enconman.2014.02.016 - 4. Nijegorodov, N., Devan, K.R.S., Jain, P.K. and Carlsson, S. (1994) Atmospheric Transmittance Models and an Analytical Method to Predict the Optimum Slope on an Absorber Plate. Renewable Energy, 4, 529-543.
http://dx.doi.org/10.1016/0960-1481(94)90215-1 - 5. Mujahid, A.M. (1994) Optimum Tilt Angle for Solar Collection Systems. International Journal of Solar Energy, 14, 191-202.
http://dx.doi.org/10.1080/01425919408909810 - 6. Calabrò, E. (2013) An Algorithm to Determine the Optimum Tilt Angle of a Solar Panel from Global Horizontal Solar Radiation. Journal of Renewable Energy, 2013, Article ID: 307547.
http://dx.doi.org/10.1155/2013/307547 - 7. Soulayman, S. (2015) Comments on “Optimum Tilt Angle for Flatplate Collectors All over the World—A Declination Dependence Formula and Comparisons of Three Solar Radiation Models” by Stanciu, C., Stanciu, D. Energy Conversion and Management, 93, 448-449.
http://dx.doi.org/10.1016/j.enconman.2015.01.005 - 8. Soulayman, S. and Sabbagh, W. (2014) An Algorithm for Determining Optimum Tilt Angle and Orientation for Solar Collectors. Journal of Solar Energy Research Updates, 1, 19-30.
http://dx.doi.org/10.15377/2410-2199.2014.01.01.3 - 9. Despotovic, M. and Nedic, V. (2015) Comparison of Optimum Tilt Angles of Solar Collectors Determined at Yearly, Seasonal and Monthly Levels. Energy Conversion and Management, 97, 121-131.
http://dx.doi.org/10.1016/j.enconman.2015.03.054 - 10. El-Kassaby, M.M. (1988) Monthly and Daily Optimum Tilt Angle for South Facing Solar Collectors; Theoretical Model, Experimental and Empirical Correlations. Solar and Wind Technology, 5, 589-596.
http://dx.doi.org/10.1016/0741-983X(88)90054-9 - 11. Skeiker, K. (2009) Optimum Tilt Angle and Orientation for Solar Collectors in Syria. Energy Conversion and Management, 50, 2439-2448.
http://dx.doi.org/10.1016/j.enconman.2009.05.031 - 12. Soulayman, S. and Sabbagh, W. (2015) Solar Collector Optimum Tilt and Orientation. Open Journal of Renewable and Sustainable Energy, 2, 1-9.
Nomenclatures
B: Tilt angle (˚).
Bopt,d: Daily optimum tilt angle (˚).
Bopt,w: Weekly optimum tilt angle (˚).
Bopt,m: Monthly optimum tilt angle (˚).
Bopt,s: Seasonally optimum tilt angle (˚).
Bopt,y: Yearly optimum tilt angle (˚).
d: Solar declination angle (˚).
G: Collector azimuth angle (˚).
H0: Extraterrestrial solar radiation (J/m2).
H: Solar radiation on Earth surface (J/m2).
L: Latitude angle (˚) which is positive for Northern Hemisphere and negative for Southern Hemisphere.
N: Day number in the year.
Wsr: Sunrise hour angle on a tilted surface (rad).
Wss: Sunset hour angle on a tilted surface (rad).
Rb: Energy gain in relation to B = 0˚ case.
Rb1: Energy gain in relation to B = L case.