Open Access Library Journal
Vol.03 No.02(2016), Article ID:68245,4 pages
10.4236/oalib.1102334
Some Studies on the Lorentz Theory of Radiation Reaction in Relation to a Charged Particle Acted on by a Constant Force in a Finite Time Interval
Rajat Roy
Department of Electronics and Electrical Communication Engineering, Indian Institute of Technology, Kharagpur, India

Copyright © 2016 by author and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 17 January 2016; accepted 1 February 2016; published 4 February 2016

ABSTRACT
An attempt to predict some experimental verification of the Lorentz theory of radiation reaction using theoretical methods is being made. The dynamics of charged particles using the equations of motion of this theory is compared to that of uncharged particles. Some verifiable consequence of pre-acceleration is also worked out.
Keywords:
Lorentz Theory of Radiation Reaction, Experimental Verification
Subject Areas: Theoretical Physics

1. Introduction
It is well known fact that the theory of radiation reaction in electrodynamics as worked out by Lorentz [1] (actually by Lorentz, Abraham and Dirac) has solutions, which exhibits a runaway nature and/or non-causal pre- acceleration. In fact the non-causal pre-acceleration without runaway makes more sense and in this paper we will only be concerned with this solution of the equation of motion. It is generally believed that the non-causal pre-acceleration exists for a short duration (typically 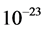 seconds for the electron) when it becomes comparable in magnitude to that of the actual acceleration and hence can never be detected in an experiment. Below we study the case of a charged particle when it is moving under the influence of a constant force preferably of a non-electromagnetic origin for a finite time duration and compare it with the dynamics of an uncharged particle of equal mass under the action of the same force. The second particle of course does not experience radiation reaction. Also we put a different initial condition and try to find out if there is some measurable parameter which detects pre-acceleration in an experiment. In the last section we discuss some difficulties with the attempts to eliminate pre-acceleration theoretically as they exist in literature [2] . Only non-relativistic dynamical equations have been used for the present and that too for one dimensional motion.
seconds for the electron) when it becomes comparable in magnitude to that of the actual acceleration and hence can never be detected in an experiment. Below we study the case of a charged particle when it is moving under the influence of a constant force preferably of a non-electromagnetic origin for a finite time duration and compare it with the dynamics of an uncharged particle of equal mass under the action of the same force. The second particle of course does not experience radiation reaction. Also we put a different initial condition and try to find out if there is some measurable parameter which detects pre-acceleration in an experiment. In the last section we discuss some difficulties with the attempts to eliminate pre-acceleration theoretically as they exist in literature [2] . Only non-relativistic dynamical equations have been used for the present and that too for one dimensional motion.
2. The Dynamical Equation of the Charged Particle with Some Initial Condition and Acted on by a Constant Force fext from 0 to t Seconds
From Equation (1.1) of ref. [1] we can write the equation of motion in one dimension as
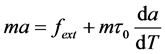 , (1)
, (1)
where 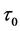 is about
is about 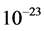 sec. for the electron and m is its mass. From Equations (1.2) and (1.3) of the same reference we can write the pre accelerated solution without runaway as
sec. for the electron and m is its mass. From Equations (1.2) and (1.3) of the same reference we can write the pre accelerated solution without runaway as
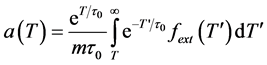 . (2)
. (2)
For the special case of 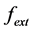 to be a constant
to be a constant 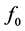 between
between 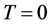 and
and 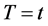 we can represent it mathematically in terms of the unit step function
we can represent it mathematically in terms of the unit step function 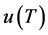 as
as
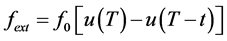 , (3)
, (3)
where 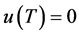 for
for 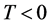 and
and 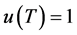 for
for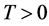 . We also prefer
. We also prefer 



The time derivative of acceleration and the velocity respectively are

and

The constant K will be zero if


where the subscript un of v denotes that it is the velocity of the uncharged particle. For 




Thus in the Lorentz theory of radiation reaction the change in kinetic energy of a radiating charged particle is equal to that of a non radiating uncharged particle when acted on by equal external forces in equal intervals of time. This fact can be determined in an experiment. The energy radiated out by the charged particle is given by the Larmor’s formula

One can easily show that this comes from the extra work done by 
3. Possible Means to Experimentally Detect Pre-Acceleration
In this section we study only the dynamics of charged particles so the restriction on 



In the non relativistic limit 



From these and using the values of 
kinetic energy from 

Since this change in kinetic energy of the particle beam before 


4. Theoretical Attempts to Cancel Pre-Acceleration in the Lorentz Theory of Radiation Reaction
Yaghjian [2] had tried to modify the existing equation of motion of the Lorentz theory of radiation reaction in a way such that pre-acceleration is excluded. He writes (see Equation (8.34) of Ref. [2] ) in place of Equation (1) of the present paper the following equation of motion expressed as per the notations used in this paper

This will first of all violate energy conservation as expressed by Equation (10) and there is no simple way to get around this difficulty if other aspects of Lorentz theory are to be kept intact after


has some features which makes it behave differently from the expression for acceleration as given by Equation (2) near


Cite this paper
Rajat Roy, (2016) Some Studies on the Lorentz Theory of Radiation Reaction in Relation to a Charged Particle Acted on by a Constant Force in a Finite Time Interval. Open Access Library Journal,03,1-4. doi: 10.4236/oalib.1102334
References
- 1. Gron, O. (2012) Electrodynamics of Radiating Charges. Advances in Mathematical Physics, 2012, Article ID: 528631.
http://dx.doi.org/10.1155/2012/528631 - 2. Yaghjian, A.D. (1992) Relativistic Dynamics of a Charged Sphere. Springer-Verlag, New York.



