Open Access Library Journal
Vol.02 No.03(2015), Article ID:68149,12 pages
10.4236/oalib.1101395
Dielectric Properties of Human Normal and Malignant Liver Tissue: A Non-Equilibrium Thermodynamics Approach
Francesco Farsaci1, Annamaria Russo2, Silvana Ficarra2, Ester Tellone2*
1Istituto per i Processi Chimico-Fisici IPCF-C.N.R., Messina, Italy
2Department of Chemical Sciences, University of Messina, Messina, Italy
Email: *etellone@unime.it
Copyright © 2015 by authors and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 March 2015; accepted 20 March 2015; published 25 March 2015
ABSTRACT
In this paper we will show the possibility of studying physical properties and irreversible phenomena that occur in biological tissues by applying the dielectric Kluitenberg’s non-equilibrium thermodynamic theory. Namely, we shall use some recent extensions of this theory that allows deducing its main characteristic parameters from experimental measurements. We determine frequency spectrum for phenomenological and state coefficients of the non-equilibrium thermodynamic approach. Applying these results to the study of human liver tumor and normal liver we show, for comparison, that it is possible to determine the difference, in some detail, of the amount of single irreversible phenomena occurring inside them.
Keywords:
Biothermodynamics, Dielectric, Spectroscopy
Subject Areas: Biophysics, Veterinary Medicine

1. Introduction
Liver cancer is the third most common cause of death from cancer worldwide. Hepatocellular carcinoma (HCC), a common cancer that typically occurs in the setting of cirrhosis and chronic hepatitis virus infections, is currently the fifth most common malignancy in men and the eighth in women worldwide [1] [2] .
The lack of distinctive pathological symptoms leads to a significant delay in the diagnosis of HCC; this often results in poor prognosis, with a median survival of a few months [3] [4] . Despite the progress in early diagnosis, the treatment options are limited, and the hepatic resection and liver transplantation are the main curative treatment [5] .
Multiple advances over the previous 30 years and the severe shortage of liver donors have expanded the indications for hepatic resection as the best treatment of this cancer, but unfortunately the vast majority of patients with liver tumors are not suitable for resection due to multifocal disease, anatomic limitations, inadequate functional liver reserve, extra-hepatic metastasis or medical co-morbidities [6] [7] .
In the last years alternative techniques have been developed, as ablation by radio frequencies, chemoembolization, radioembolization, magnetic chemotherapy and cryo-ablation, for local treatment of the liver tumour [8] - [12] .
In particular by means of new microwave ablation (MWA) techniques good results have been obtained. This technique consists in the insertion of a microwave antenna that, by suitable frequencies of electromagnetic wave, causes cellular coagulation necrosis of the tumour.
The potential advantages of microwave technology include consistent production of high intra-tumoral temperatures, fast ablation times, large tumor ablation volumes and the use of multiple antennae; also it does not require the use of grounding pads, which decreases the time required for patient preparation [13] [14] .
However, few data are available on the extent of tumour destruction possible with microwave ablation, which are now used in conventional microwave ovens given optimal heating profiles [15] - [17] . Tissue damage during an ablation procedure is a function of the time-temperature history, which is directly related to the interaction of microwaves with the tissue. For this reason, the knowledge of dielectric properties of the liver, when it is subjected to electromagnetic perturbation in the range of microwave frequencies, may open new perspectives for the further development of MWA techniques.
Unfortunately, few studies have reported dielectric properties of tumour and normal liver tissues; the insufficient number of data is an handicap for the development of MWA techniques because physiological behaviour, as perfusion with temperature and water content change, affects dielectric properties of the biological tissue showing a substantial difference between physiological and pathological, and between living and non-living tissue.
Our goal is to deepen the study of dielectric properties of liver samples in the microwave frequency range investigating in the context of non-equilibrium thermodynamics (NET) [18] . In fact, biological tissues are characterized by a plethora of complex irreversible processes ideally framed in the framework of NET, which should be taken into account when analysing the bio-physical properties of a tissue, such as the dielectric and the mechanic relaxation phenomena [19] [20] .
In particular, we shall apply some recent theoretical methodologies in NET [21] - [25] , in order to approximately deduce the frequency spectrum of the so-called phenomenological and state coefficients. These coefficients, fundamental in NET, have the role of relating entropy sources to irreversible processes that occur inside a medium. Thus, they summarize some physical phenomena occurring in the medium in study.
1.1. Non-Equilibrium Thermodynamics (NET)
A central point of the formalism of NET is the definition of appropriate thermodynamic generalized forces (also called affinities) and fluxes in order to fully represent the entropy variation. Generalized forces and fluxes are connected by relationships, called phenomenological equations, which in many cases can be considered linear. The coefficients of those linear relationships are called phenomenological coefficients [18] . Of course, these coefficients (constant in time) are dynamically varying and they depend on the frequency spectrum of the excitations.
A more deep insight in the underlying phenomena is obtained by the Kluitenberg’s thermodynamic theory [26] - [28] by means of the definition of some other linear relationships, called state equations, in which appear the so called state coefficients. Indeed, they allow to qualitatively discriminate among classes of phenomena, and to provide quantitative estimate.
A strong limitation of the applicability of this theory is that an exact analytical computation of these coefficients is often impossible. However, recently approximate analytical expression of the dependence of the dielectric phenomenological and state coefficients on the frequency have been proposed [24] [25] . This approach, successfully applied to measurements on some polymeric non-biological materials, allows to infer the coefficients from experimental measurements, overcoming the above-mentioned classical limit in the application of NET’s theories.
The proposed approach constitutes an advancement with respect to traditional measurements of dielectric (or mechanical) properties. Indeed, standard dielectric (or mechanic) measurements of complex physical systems are only able to obtain complex dielectric constant (or complex Young module) [21] . Those modules give only global information about the reversible and irreversible phenomena which occur in the medium and do not specify the amount of the particular phenomena which give rise to them. Our new approach allows to a more detailed investigation since it allows to determine the amount of single phenomena which are hidden in the medium by means of the relationships, between the aforementioned coefficients and the measured complex dielectric constant.
We state that our point of view is in agreement with the assertion that physical principles are valid even for biological materials and that the greater difficulty to apply them is the identification of the variables that are to be considered as input in a contest of cause-effect principle. Since we are interested only to dielectric properties of human normal and malignant liver tissue and so to the difference between them we will consider the aforementioned coefficient as a function of the electric harmonic perturbation to which the tissue is subject. In particular as function of the frequency of harmonic perturbations.
1.2. Theoretical Thermodynamic Approach
The Kluitenberg’s theory [28] postulates that the usual variables of non-equilibrium thermodynamic are insufficient for study a medium that is subject to perturbations.
Generally, the specific entropy “s” will be (for an elastic dielectric) function of the specific internal energy u, the strain tensor εik and the specific polarization  [26] - [28] . Kluitenberg introduced a new vector field p(1) and rewrote the entropy as
[26] - [28] . Kluitenberg introduced a new vector field p(1) and rewrote the entropy as
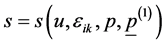 (1)
(1)
This lead to the following variables
 (2)
(2)
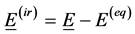 (3)
(3)
where 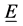 is the electrical field that appear in the Maxwell equations. The introduction of the vector
is the electrical field that appear in the Maxwell equations. The introduction of the vector  allows to decompose the polarization p as the sum of
allows to decompose the polarization p as the sum of 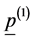 and of a vector
and of a vector  defined as:
defined as:
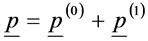 (4)
(4)
and therefore to the introduction of the electric field E(1) correlated to  as follows:
as follows:
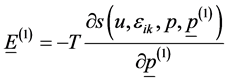 (5)
(5)
By defining: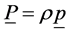 , for isotropic media one can infer the following phenomenological relationships [28] :
, for isotropic media one can infer the following phenomenological relationships [28] :
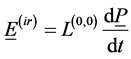 (6)
(6)
 (7)
(7)
and the following state equations
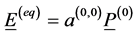 (8)
(8)
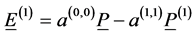 (9)
(9)
where possible cross-effects among dielectric relaxation and other irreversible phenomena were neglected, and it is assumed that the mass density ρ is constant.
L(0,0) and L(1,1) are called phenomenological coefficients, whereas a(00) and a(11) state coefficients. We report the physical meaning to them associated:
a(00) and a(11) reciprocal dielectric constants
L(00) resistance
L(11) conductivity
We emphasize that L(0,0) and L(1,1) are not related to conduction current, but only to displacement one.
Combining Equations (6)-(9) it can be shown that the following differential equation for dielectric relaxation phenomena can be obtained:

where

In that which follows we refer only to one-dimension problem and so we consider only scalar quantity. In agreement with linear response theory [19] [29] , by assuming that P (as cause, extensive variable) vary as

it follows that E (as effect, intensive variable) vary as

were ϕ(ω) is the phase lag between P and E.
By indicating with Г1 e Г2 storage and loss dielectric moduli respectively and remembering that they are related to no dissipative and dissipative phenomena respectively we have [19] [29] :

and the following expression for phenomenological and state coefficients as function of the frequency can be obtained:

where σ is the relaxation time and we have introduced a new quantity defined as:

By remembering the meaning of Г2 the last equation represents the difference between the total loss modulus and the loss associated to E(ir) (E(ir) and therefore L(00) are not related to internal degree of freedom); in other words Equation (16) represents the dissipation associated to internal degree of freedom.
From 151 and 153 it follows that, if


And from (18) and (7) it follows

and from (4) we obtain:

Moreover from Equation (5) we deduce that E(1) is not defined and therefore a(1,1) is not defined. This means that no internal degree of freedom appears in agreement with physical meaning of
From Equations (8) and (9) we see that

This means that the difference between a(0,0) and a(1,1) is related to the difference between E(1) and E(eq). In particular if a(0,0) = a(1,1) it follows

We observe that 


It is to note that, although no internal variables appear, we are not in an equilibrium state because Г2 = ωL(00) is different from zero.
Now it is easy to see that if Г2 = 0 it follows 

where T is the temperature (which we have assumed constant). In fact the Equation (30) is the sum of the only two dissipative terms:
1) dissipation related to E(ir) (see Equation (6))
2) dissipation related to int. degree of freedom (see Equation (16))
If both are equal to zero, the system is in equilibrium state with zero entropy production.
In brief:
If
If
It is easy to consider the case in which L(00) = 0; in this case 
2. Materials and Methods
In this paper the results obtained by O’Rourke et al. [30] have been reviewed with regard to the in vivo relative complex permittivity and in vivo effective conductivity. Our approach is based on the assumption (supported by experiments) that in biological tissue hidden electrical phenomena occur which correspond to internal degree of freedom. The latter must be taken into account for a more detailed description and therefore for prediction.
In the contest of NET [28] hidden electrical phenomena are well described by some functions related to coefficients that appear in the theory and characterize the medium by a physical point of view. We will consider the aforementioned coefficients as a function of the electric harmonic perturbation to which the liver tissue is subject.
This new approach enables a more detailed investigation since it allows determining the amount of single phenomena which are hidden in the tissue by means of the relationships, among the coefficients mentioned above and the complex dielectric constant measured.
3. Results and Conclusions
We indicate the function referred to pathological and normal tissues with the index “p” and “n” respectively. In this section we analyze experimental results for normal and pathological tissue taking into account the theoretical results described above. In particular we will investigate dissipative phenomena and therefore we start by analyzing the modulus G2.
By observing the Figure 1(b) we note that two regions of frequency exist; these are the range of w for which it results G2p < G2n, which we call “low frequency region”, and the range of w for which it results G2p > G2n, which we call “high frequency region”. By remembering the meaning of the modulus G2, the two curves show a greater dissipation of the pathologic tissue with respect to normal one in the region of high frequency (G2p > G2n); on the contrary a greater dissipation of the normal tissue with respect to pathologic one is shown in the region of low frequency (G2p < G2n).
It is easy to see that this change can be associated to the change of 
1)
2)
This means that for low frequencies, for which condition 2) is valid (Figure 1(b)) dissipation due to variation of P (Equation (6)) is predominant on that due to internal degree of freedom.
On the contrary, for high frequencies, for which condition 1) is valid (Figure 1(b)), dissipation due to internal degree of freedom is predominant on that due to variation of P (Equation (6)).
So, in agreement with the entropy production (Equation (24)) we have two types of dissipation phenomena.
1) due to
2) due to ωL(00)
The first is associated to the phenomenological L(1,1) and to the state coefficient a(0,0) (we do not consider a(1,1) because it shows the reciprocal trend with respect to L(1,1) (Equation (15)2,3). The second to phenomenological coefficient L(0,0).
For that which concern L(1,1) (Figure 2(b)) we can observe an appraisable increment of 




Figure 1. (a) Storage modulus for normal and malignant liver tissue; (b) Loss modulus for normal and malignant liver tissue; (c) Dissipation by internal degree of freedom for normal and malignant liver tissue.



Figure 2. (a) State coefficient for normal and malignant liver tissue; (b) Phenomenological coefficients for normal and malignant liver tissue; (c) Phenomenological coefficients for normal and malignant liver tissue.
By physical meaning of L(1,1) we deduce that dissipation due to conductivity in the region of high frequencies is greater in pathological tissue then normal one.
Moreover it is very important to observe that the increment of 



Generally, in the differentiated form, the neoplastic cell have eosinophilic and cuboidal cytoplasm; vesicular nuclei with prominent nucleoli. Tumor cells show an increase in size with inverse nucleus/cytoplasm ratio [30] - [32] .
This can be the motivation of the increase of the coefficient L(1,1) and so of the conductivity shown in Figure 1(c) and Figure 2(b) (we will emphasize that this result is obtained only by dielectric measurements and no other test are necessary). These cells are very similar to normal hepatocytes as to be sometimes difficult to distinguish by themselves, especially in cytological smears. The histological structure tends to reproduce the architecture of the normal liver, in laminae or trabeculae of variable thickness separated by sinusoids lined with endothelium and very scarce reticular structure [31] [32] . For that which concern the phenomenological coefficient L(0,0) (Figure 2(c)) we see that it decreases with frequency increasing but in such a way that it results ωL(00) = G2R = constant. Moreover Figure 2(c) shows a greater dissipation of normal tissue with respect to pathologic one due to variation of P.
For that which concern a(0,0) we see that 




It is important to observe that 
The behavior of 



In brief:
low frequency
high frequency
Finally we analyze the entropy production. Observing Figure 3 we note that pathological tissue shows a lesser entropy production than normal one. This means that inside pathological tissue the phenomena occur in such a way to result “more reversible”.
We will conclude by specifying that the hope of this work is to suggest a new point of view based on application of no equilibrium thermodynamics with internal variables (internal degree of freedom) formulated by Kluitenberg and developed, for an experimental approach, by us (in previous papers) [20] - [25] .
We are conscious of the difficulties to adapt the mathematical model of the aforementioned theory to the very complex phenomena that occur in biological tissues, but we are sure that the development of these ideas can lead to new results as it has been showed in this paper.
Figure 3. Entropy production for normal and malignant liver tissue.
An analogous approach can be used if we investigate the tissues by mean of mechanical perturbation [33] [34] or sound wave perturbation (ultra-sound wave) [35] . In this last case the coefficients obtained can give preventive information on tumors presence directly by mean of ecographic devices earlier than usual techniques.
Cite this paper
Francesco Farsaci,Annamaria Russo,Silvana Ficarra,Ester Tellone, (2015) Dielectric Properties of Human Normal and Malignant Liver Tissue: A Non-Equilibrium Thermodynamics Approach. Open Access Library Journal,02,1-12. doi: 10.4236/oalib.1101395
References
- 1. Jemal, A., Ward, E., Hao, Y. and Thun, M. (2005) Trends in the Leading Causes of Death in the United States, 1970-2002. The Journal of the American Medical Association, 294, 1255-1259.
http://dx.doi.org/10.1001/jama.294.10.1255 - 2. Bosch, F.X., Ribes, J., Díaz, M. and Cléries, R. (2004) Primary Liver Cancer: Worldwide Incidence and Trends. Gastroenterology, 127, S5-S16.
http://dx.doi.org/10.1053/j.gastro.2004.09.011 - 3. Forner, A., Hessheimer, A.J., Real, M.I. and Bruix, M.J. (2006) Treatment of Hepatocellular Carcinoma. Critical Reviews in Oncology/Hematology, 60, 89-98.
http://dx.doi.org/10.1016/j.critrevonc.2006.06.001 - 4. Kew, M.C., Dos Santos, H.A. and Sherlock, S. (1971) Diagnosis of Primary Cancer of the Liver. British Medical Journal, 4, 408-411.
http://dx.doi.org/10.1136/bmj.4.5784.408 - 5. Zhang, B.H., Yang, B.H. and Tang, Z.Y. (2004) Randomized Controlled Trial of Screening for Hepatocellular Carcinoma. Journal of Cancer Research and Clinical Oncology, 1307, 417-422.
- 6. Bruix, J. and Sherman, M. (2005) Management of Hepatocellular Carcinoma. Hepatology, 42, 1208-1236.
http://dx.doi.org/10.1002/hep.20933 - 7. Llovet, J.M., Burroughs, A. and Bruix, J. (2003) Hepatocellular Carcinoma. The Lancet, 362, 1907-1917.
http://dx.doi.org/10.1016/S0140-6736(03)14964-1 - 8. Garcea, G., Lloyd, T.D., Aylott, C., Maddern, G. and Berry, D.P. (2003) The Emergent Role of Focal Liver Ablation Techniques in the Treatment of Primary and Secondary Liver Tumours. European Journal of Cancer, 39, 2150-2164.
http://dx.doi.org/10.1016/S0959-8049(03)00553-7 - 9. Wright, A.S., Mahvi, D.M., Haemmerich, D.G. and Lee Jr., F.T. (2003) Minimally invasive approaches in management of hepatic tumors. Surgical Technology International, 11, 144-153.
- 10. Wright, A.S., Sampson, L.A., Warner, T.F., Mahvi, D.M. and Lee Jr., F.T. (2005) Radiofrequency versus Microwave Ablation in a Hepatic Porcine Model. Radiology, 236, 132-139.
http://dx.doi.org/10.1148/radiol.2361031249 - 11. Stańczyk, M., Zegadło, A., Zwierowicz, T., Zak, D., Bogusławska, R. and Maruszyński, M. (2009) Microwave Ablation of Liver Tumors as a New Instrument for Minimally Invasive Liver Surgery. Polski Merkuriusz Lekarski, 26, 545-549.
- 12. Lloyd, D.M., Lau, K.N., Welsh, F., Lee, K.F., Sherlock, D.J., Choti, M.A., Martinie, J.B. and Iannitti, D.A. (2011) International Multicentre Prospective Study on Microwave Ablation of Liver Tumours: Preliminary Results. HPB (Oxford), 13, 579-585.
- 13. Stauffer, P.R., Rossetto, F., Prakash, M., Neuman, D.G. and Lee, T. (2003) Phantom and Animal Tissues for Modelling the Electrical Properties of Human Liver. International Journal of Hyperthermia, 19, 89-101.
http://dx.doi.org/10.1080/0265673021000017064 - 14. Wright, A.S., Lee Jr., F.T. and Mahvi, D.M. (2003) Hepatic Microwave Ablation with Multiple Antennae Results in Synergistically Larger Zones of Coagulation Necrosis. Annals of Surgical Oncology, 10, 275-283.
http://dx.doi.org/10.1245/ASO.2003.03.045 - 15. Shock, S.A., Meredith, K., Warner, T.F., Sampson, L.A., Wright, A.S., Winter 3rd, T.C., Mahvi, D.M., Fine, J.P. and Lee Jr., F.T. (2004) Microwave Ablation with Loop Antenna: In Vivo Porcine Liver Model. Radiology, 231, 143-149.
http://dx.doi.org/10.1148/radiol.2311021342 - 16. Hines-Peralta, A.U., Pirani, N., Clegg, P., Cronin, N., Ryan, T.P., Liu, Z. and Goldberg, S.N. (2006) Microwave Ablation: Results with a 2.45-GHz Applicator in ex Vivo Bovine and in Vivo Porcine Liver. Radiology, 230, 94-102.
http://dx.doi.org/10.1148/radiol.2383050262 - 17. Jiao, D.C., Zhou, Q., Han, X.W., Wang, Y.F., Wu, G., Ren, J.Z., Wang, Y.L., Ding, P.X., Ma, J. and Fu, M.T. (2012) Microwave Ablation Treatment of Liver Cancer with a 2,450-MHz Cooled-Shaft Antenna: Pilot Study on Safety and Efficacy. Asian Pacific Journal of Cancer Prevention, 13, 737-742.
http://dx.doi.org/10.7314/APJCP.2012.13.2.737 - 18. De Groot, S.R. and Mazur, P. (1984) Non-Equilibrium Thermodynamics. Dover Publication, New York.
- 19. McCrum, N.G., Read, B.E. and Williams, G. (1967) Anelastic and Dielectric Effects in Polymeric Solids. John Wiley and Sons Ltd., London.
- 20. Farsaci, F., Tellone, E., Cavallaro, M., Russo, A. and Ficarra, S. (2013) Low Frequency Dielectric Characteristics of Human Blood: A Non Equilibrium Thermodynamic Approach. Journal of Molecular Liquids, 188, 113-119.
http://dx.doi.org/10.1016/j.molliq.2013.09.033 - 21. Ciancio, V., Farsaci, F. and Di Marco, G. (2007) A Method for Experimental Evaluation of Phenomenological Coefficients in Media with Dielectric Relaxation. Physica B, 387, 130-135. http://dx.doi.org/10.1016/j.physb.2006.03.095
- 22. Ciancio, V., Farsaci, F. and Rogolino, P. (2009) Phenomenological Approach on Wave Propagation in Dielectric Media with Two Relaxation Times. Physica B, 404, 320-324.
http://dx.doi.org/10.1016/j.physb.2008.11.070 - 23. Ciancio, V., Farsaci, F. and Rogolino, P. (2009) On the Extension of Debye’s Model for Media with Dielectric Relaxation. International Journal of Engineering Mathematics, 1, 57-63.
- 24. Farsaci, F. and Rogolino, P. (2012) An Alternative Dielectric Model for Low and High Frequencies: A Nonequilibrium Thermodynamic Approach. Journal of Non-Equilibrium Thermodynamics, 37, 27-41.
- 25. Ciancio, V., Farsaci, F. and Rogolino, P. (2010) On a Thermodynamical Model for Dielectric Relaxation Phenomena. Physica B, 405, 175-179.
http://dx.doi.org/10.1016/j.physb.2009.08.047 - 26. Kluitenberg, G.A. (1973) On Dielectric and Magnetic Relaxation Phenomena and Non-Equilibrium Thermodynamics. Physica, 68, 75-82.
http://dx.doi.org/10.1016/0031-8914(73)90131-6 - 27. Kluitenberg, G.A. (1977) On Dielectric and Magnetic Relaxation Phenomena and Vectorial Internal Degrees. Physica A, 87, 302-330.
http://dx.doi.org/10.1016/0378-4371(77)90019-X - 28. Kluitenberg, G.A. (1981) On Vectorial Internal Variables and Dielectric and Magnetic Relaxation Phenomena. Physica A, 109, 91-122.
http://dx.doi.org/10.1016/0378-4371(81)90039-X - 29. Ciancio, V., Farsaci, F. and Rogolino, P. (2009) Mathematical Approach to the Relaxation Phenomena. Applied Sciences, 11, 48-59.
- 30. O’Rourke, A.P., Lazebnik, M., Bertram, J.M., Converse, M.C., Hagness, S.C., Webster, J.G. and Mahvi, D.M. (2007) Dielectric Properties of Human Normal, Malignant and Cirrhotic Liver Tissue: In Vivo and ex Vivo Measurements from 0.5 to 20 GHz Using a Precision Open-Ended Coaxial Probe. Physics in Medicine and Biology, 52, 4707-4719.
http://dx.doi.org/10.1088/0031-9155/52/15/022 - 31. Baker, P.M., Clement, P.B. and Young, R.H. (2005) Malignant Peritoneal Mesothelioma in Women. A Study of 75 Cases with Emphasis on Their Morphologic Spectrum and Differential Diagnosis. American Journal of Clinical Pathology, 123, 724-737.
http://dx.doi.org/10.1309/2H0NVRERPP2LJDUA - 32. Bai, X. and Wu, C.L. (2012) Renal Cell Carcinoma and Mimics: Pathologic Primer for Radiologists. AJR, 198, 1289-1293.
- 33. Ciancio, V., Bartolotta, A. and Farsaci, F. (2007) Experimental Confirmations on a Thermodynamical Theory for Viscoanelastic Media with Memory. Physica B—Condensed Matter, 394, 8-13.
http://dx.doi.org/10.1016/j.physb.2007.01.031 - 34. Farsaci, F., Ciancio, V. and Rogolino, P. (2010) Mechanical Model for Relaxation Phenomena in Viscoanelastic Media of Order One. Physica B—Condensed Matter, 405, 3208-3212.
http://dx.doi.org/10.1016/j.physb.2010.03.016 - 35. Ciancio, A., Ciancio, V. and Farsaci, F. (2007) Wave Propagation in Media Obeying a Thermoviscoanelastic Model. Scientific Bulletin—University Politehnica of Bucharest, Series A: Applied Mathematics and Physics, 69, 69-79.
Abbreviations
Hepatocellular carcinoma (HCC);
Microwave ablation (MWA);
Non-equilibrium thermodynamics (NET).
NOTES
*Corresponding author.














