Received 1 March 2015; accepted 16 March 2015; published 20 March 2015

ABSTRACT

The article shows that to suppress the rotational motion of the air, form a funnel with a diameter of 200 m and the velocity of rotational movement of its walls equal to V = 100 m/s, it is required to pour 80 tons of liquid nitrogen into the funnel.

Keywords:

Tornado

Subject Areas: Atmospheric Sciences

1. Introduction

The region of the rotational motion of the air, which is also observed in the vertical movement of air masses, is called a tornado [1] .

The rotational movement is realized in a vortex under the action of the centripetal force generated by the difference of static pressures (P_out and P_in) multiplied by the corresponding area of the tornado walls:

(1)

We take the diameter of the tornado funnel at the earth surface equal to d_funnel = 200 m, and let the height of the funnel be equal to H = 1 km [1] . Then the volume of the funnel Vol_funnel is as follows:

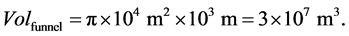(2)

2. Structure of the Tornado Given by V. V. Kushin

In [2] , V. V. Kushin analyzed parameters of tornadoes observed in nature and gave these parameters in the diagram (Figure 1). In the diagram this area is highlighted in red.

The vertical axis represents the rotational velocity of the wall of a tornado, which we denote by V_t. It can be

seen that the tornadoes have V_t within a narrow range of velocities: 60 m/s < V_t < 160 m/s.

The horizontal axis shows the value of 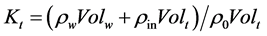equal to the ratio of the funnel mass to the mass of the air displaced by the funnel. Here ρ_w―density of the wall of the funnel, 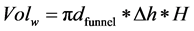―volume of the tornado wall, Δh―the wall thickness of the funnel, H―height of the funnel. The density of the air inside the funnel is ρ_in, the volume Vol_t of the funnel is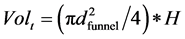, r₀ = 1.3 kg/m³ is the density of air under normal conditions.

According to the ideas presented in [2] , the relation of the internal pressure to the pressure outside the tornado ―can vary quite widely. Numbers 1 - 5 in Figure 1 show the curves with the parameter 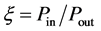equal to ξ = 0, 0.25, 0.5, 0.75 and 0.9. It is seen that the relation above can vary within ξ = 0.25 - 0.9.

Since the relation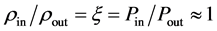, the expression for K_t can be written as follows:

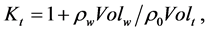(3)

where the second term shows how many times the mass of the walls of the tornado exceeds the mass of the air pressed out by the tornado. This formula shows that K_t is always greater than 1.

Indeed, if K_t were less than 1, the tornado would not have fallen onto the earth but sailed in the air. The volume of the walls of a typical tornado is about 5 times less than the volume of the funnel of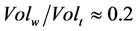. The density of the material in the walls is by about 10 - 20 times higher than the density of air under normal conditions ρ_w/ρ₀ ≈ 10 - 20, so that a typical value of K_t = 3 - 5.

The density of the air and water vapor in the tornado walls ρ_w1 in this case is only by 3 times higher than the air density under normal conditions ρ_w1 = 4 g/cm². Why it happens so is not clear. The dynamical pressure calculated on the Bernoulli formula is equal to the following:

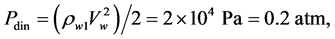(4)

i.e.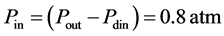, , 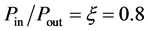that corresponds to the curve (4) in Figure 1.

The dynamic pressure of the rain drops in the walls of a tornado is equal to the following:

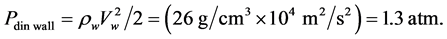(5)

At this pressure the tornado walls cut trees approximately like a rotating blade of the electric razor cuts the hair.

The water in the walls of a tornado is not involved in the creation of the pressure difference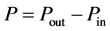, which is determined only by density ρ_w1 = 4 g/cm³.

3. Vertical Movement of Air

In nature there is a vertical pressure gradient associated with the gravitational field [2] . This gradient is caused by the fact that the air in the atmosphere is stirred continuously. When the air is moving upwards it expands and cools since the pressure decreases with height. When it is moving downwards, it is heated, respectively. The temperature gradient dT/dx is expressed by a well-known formula:

,

where R₀ = 287 J/(kg∙degree)―the universal gas constant, g―acceleration of the free fall, γ―adiabatic coefficient. For the diatomic gas, i.e.―the air, γ = 1.4, therefore, dT/dx ≈ 10 degree/km.

We call this temperature gradient “static”.

Let the air have a vertical temperature gradient equal to ΔT = 10 degree at a height H = 1 km. We call this temperature gradient “dynamic”.

This temperature gradient will cause a vertical pressure gradient equal to

(6)

where P₀ = 10⁵ Pa―the normal atmospheric pressure, ΔT = 10 degree―the temperature gradient, T₀ = 300 K is the room temperature. Then from (6) it follows that.

This vertical dynamic pressure gradient will result in vertical movement of the air. The velocity of this vertical air movement can be determined from the following ratio:

, (7)

where for ρ = 1 kg/m³, H = 1 km, d_funnel = 200 m. Thus, the vertical velocity is equal to V_vert = 17 (m/s).

It is not difficult to show that the vertical movement of the air with a velocity V_vert = 17 m/s is able to rise up a water balloon with a diameter of 1 cm.

Indeed, the dynamic pressure in this case is equal to the following:

When the cross-section of the ball S_tr ≈ 1 cm², the lift force for this ball will be equal to 1.5 × 10³ dn. In the units of mg it is equal to 1.5 gram forces. That is more than the force of gravity acting on a water balloon with a diameter of 1 cm.

The lighter warm air rises up inside the tornado, lifting up the items which happen to be inside the tornado.

4. Influence of Liquid Nitrogen

4.1. Alignment of the Pressure outside and inside of the Tornado Funnel

An obvious way to disrupt the rotational motion in a tornado is to create the pressure difference P_in-out equal to the magnitude of the difference between the static pressures. Then the centripetal force will disappear―it holds the water in the walls of the tornado on circular orbits and then the mode of the rotational motion of rain in the walls of the tornado will fail.

Let us calculate the quantity of liquid nitrogen to be poured inside the tornado to cease the rotational movement of the tornado walls.

The calculations will be carried out for the vertical tube section with a height of H₁ = 50 m. We will find the required conditions to break the tornado “trunk” and lift it up over the ground to a height of H₁ = 50 m. In this case this area will be filled with non-rotating air and the pressure difference P_out − P_in, which causes the rotational motion, will disappear.

Moreover, it is not necessary to reduce the pressure difference to zero inside and outside of the tornado funnel. According to the graph shown in Figure 1, it is enough to increase the pressure inside the tornado even by 0.1 atm to go from curve (4) to curve (5). Curve (4) corresponds to the relation of the pressure inside the tornado to the pressure outside it:, and the curve (5) corresponds to value, for which a tornado does not exist in nature.

Assuming that the density of nitrogen in the gaseous state is equal to [2] , p. 57, and in the liquid state, we find that the ratio of the density of nitrogen in the liquid state to the density of the gaseous nitrogen is equal to.

This means that in order to fill the funnel having a volume of 1.5 × 10⁶ m³ with nitrogen and create the extra pressure P = 0.1 atm, it is necessary to implant 1.5 × 10⁶ × 1.25 × 0.1 ≈ 200 ton of liquid nitrogen into the funnel. In the liquid state this volume of nitrogen will be equal to.

4.2. Alignment of the Vertical Temperature Gradient inside the Funnel

The heat capacity of nitrogen is [3] , p. 142,. If we consider that 1 mole of nitrogen is equal to 28 grams, we can approximately calculate that the specific heat of nitrogen is equal to 1 J/(g∙degree) or 1 MJ/(ton∙degree). So, to heat 200 ton of nitrogen having the temperature from 195˚C to 25˚C, it is necessary to use 200 × 220 = 4.4 × 10¹⁰ J of energy.

The heat of the phase transition from liquid―gas for nitrogen is equal to [3] , p. 193, or 200 MJ/ton. For 200 ton it is required to spend 200 ton × 200 MJ/ton ≈ 4 × 10¹⁰ J. Thus, the total energy expenses to evaporate nitrogen and heat it to the temperature of 25˚C, is equal to 9 × 10¹⁰ J.

The heat capacity of air is 1 kJ/(kg∙degree), and the air inside the segment having the length of 50 meters, has a mass of 1.5 × 10⁶ m³ × 1.3 kg/m³ = 2 × 10⁶ kg. So, to cool this air mass by one degree, it will be required to spend 2 × 10⁹ J/(1 degree) of energy.

Evaporation of liquid nitrogen and its heating will result in cooling of the total mass of the air inside the funnel: 9 × 10¹⁰ J/[2 × 10⁹ J/(1degree)] by 45 degrees of Celsius.

This will increase the pressure inside the funnel: by the magnitude ΔP_vert1 ≈ 10⁵ × (45/300) = 1.5 × 10⁴ Pa. This pressure is higher than the pressure of 10⁴ Pa, which is created by the extra mass of nitrogen. So, to break the rotational motion of the air and water in the walls of a tornado, it will be required to use a less mass of nitrogen―about 80 ton.

5. Conclusion

Taking into account all the above, it is clear that the use of liquid nitrogen can result in breaking of the rotational movement of air inside the tornado. Perhaps, the height of H₁ = 50 m, to which, as we consider, the tornado “jumps” is too high. The height of 10 meters may be enough for the tornado “to jump” and it will require a smaller amount of liquid nitrogen than we have calculated.

Cite this paper

Sergey Niikolayevich Dolya, (2015) An Opportunity of Failure of the Air Rotational Motion. Open Access Library Journal,02,1-4. doi: 10.4236/oalib.1101403

References