 International Journal of Geosciences, 2011, 2, 293-309 doi:10.4236/ijg.2011.23032 Published Online August 2011 (http://www.SciRP.org/journal/ijg) Copyright © 2011 SciRes. IJG Adapted Caussinus-Mestre Algorithm for Networks of Temperature Series (ACMANT) Peter Domonkos Centre for Climate Change (C3), Geography Department, University Rovira i Virgili, Campus Terres de l’Ebre, Tortosa, Spain E-mail: peter.domonkos@urv.cat Received March 19, 2011; revised April 28, 2011; accepted June 1, 2011 Abstract Any change in technical or environmental conditions of observations may result in bias from the precise values of observed climatic variables. The common name of these biases is inhomogeneity (IH). IHs usually appears in a form of sudden shift or gradual trends in the time series of any variable, and the timing of the shift indicates the date of change in the conditions of observation. The seasonal cycle of radiation intensity often causes marked seasonal cycle in the IHs of observed temperature time series, since a substantial portion of them has direct or indirect connection to radiation changes in the micro-environment of the thermometer. Therefore the magnitudes of temperature IHs tend to be larger in summer than in winter. A new homogenisa- tion method (ACMANT) has recently been developed which treats in a special way the seasonal changes of IH-sizes in temperature time series. The ACMANT is a further development of the Caussinus-Mestre method, that is one of the most effective tool among the known homogenising methods. The ACMANT applies a bivariate test for searching the timings of IHs, the two variables are the annual mean temperature and the amplitude of seasonal temperature-cycle. The ACMANT contains several further innovations whose effi- ciencies are tested with the benchmark of the COST ES0601 project. The paper describes the properties and the operation of ACMANT and presents some verification results. The results show that the ACMANT has outstandingly high performance. The ACMANT is a recommended method for homogenising networks of monthly temperature time series that observed in mid- or high geographical latitudes, because the harmonic seasonal cycle of IH-size is valid for these time series only. Keywords: Statistical Method Development, Observed Climatic Data, Temperature, Time Series Analysis, Data Quality Control, Homogenization, Efficiency 1. Introduction For achieving reliable information about climate vari- ability, large amount of observed time series of high quality is needed. One principal tool for improving data quality is the application of statistical homogenisation. In the recent decades large number of homogenisation methods have been developed and applied for homoge- nising climatic time series. In these methods wide range of statistical tools are applied for detecting change-points or trends of non-climatic origination (i.e. inhomogenei- ties [IH]) in observed meteorological time series. The main tools of IH detection are 1) examination of accu- mulated anomalies [1], 2) rank-order statistics [2,3], 3) multiple linear regression [4,5], 4) t-test based examina- tions [6,7], 5) multiple analysis with Fisher-test [8], 5) fitting step-function [9]. Looking through reviewing arti- cles about homogenisation methods [10-17] it can be seen that we know many details about homogenisation methods, but uncertainties still exist about their efficien- cies, or with other words, about the practical usefulness of individual methods. The recently developed ACMANT homogenisation method has some characteristics those are absolutely new, and may influence positively the effectiveness of homo- genisation. The most important innovation in ACMANT is that it uses bi-variable test for detecting IHs in monthly series of temperatures. The two variables are the annual mean temperature and the amplitude of seasonal cycle. Considering that the sizes of IHs in temperature series often have seasonal cycle of considerable ampli- tude [18,19], the selected two variables often have  P. DOMONKOS 294 change-points in the same time. The chance of right de- tection increases when the change-points with common time-points are searched with unified test for the two variables. In ACMANT IHs with gradually changing deviation from the correct values are approached by se- ries of change-points, similarly as in many other ho- mogenisation methods. The paper describes the operation of the whole homo- genisation procedure, discusses its general properties, and gives information about its effectiveness. The orga- nisation of the paper is as follow: The next section gives a general picture about the main properties of ACMANT, and describes the conditions of its practical application. Section 3 describes the main functions of ACMANT in detailed. In section 4 the operation of ACMANT is summarised and its steps are presented in the true se- quence. In section 5 some verification results are pre- sented. Finally, in section 6, the properties of ACMANT and the verification results are discussed, and conclu- sions are drawn. The paper has an appendix with the ex- planation of symbols applied. 2. Main Properties of ACMANT 1) A fully automated method. 2) The use of ACMANT is recommended for tem- perature series from mid- and high-latitudes, since its algorithm supposes quasi-harmonic annual cycle of con- siderable amplitude in IH-sizes. 3) Relative homogenisation method, thus it can be used for networks, and not for solely time series. Basi- cally, the ACMANT applies the traditional comparison of candidate series—reference series pairs. Reference series are always built from minimum two component series. A speciality of ACMANT that if the time series of the network have observed values for different time pe- riods, it may use different reference series for different sections of the same candidate series and the selection of reference series is automatic. 4) ACMANT incorporates the best detection and cor- rection algorithms of known homogenisation methods, i.e. the detection part is based on the PRODIGE [9] method, while the final correction of time series is made with ANOVA [9]. 5) Main novelties of ACMANT relative to PRODIGE: a) It applies the Caussinus—Mestre detection method jointly to two variables, i.e. to annual means, and sum- mer-winter differences; b) Fully automatic generation of reference series, c) Pre-homogenisation for preparing composites of reference series of better quality than in the raw dataset, d) Separated way of detection for long-term IHs and short-term IHs; e) After the calcula- tion of correction-terms by ANOVA, those IHs that turn out to be insignificant are deleted from the list of IHs, and the ANOVA procedure is repeated with a reduced list of IHs. 6) Two types of IH-detection are included in ACMANT, i.e. the Main Detection is for long-term IHs (generally with at least 3 years duration), while the Sec- ondary Detection is for large-size but short-term IHs. Both detection segments are developed from the Caussi- nus-Mestre detection algorithm. 7) The lengths of raw time series in a network can be different, and they may cover different time periods. Any candidate time series or a section of candidate series is subdued to homogenisation with ACMANT if at least two partner time series exist in the network that cover the period of the candidate series or its section and have at least 0.5 autocorrelation with the candidate series. 8) Time series often contain large number of missing values. If the ratio of missing values exceeds some preset thresholds in some section(s) of the time series that sec- tions are classified non-applicable sections, while the section with acceptable ratio of available data is the ap- plicable section. According to this, raw time series are generally split into three sections, i.e. one applicable sec- tion and two non-applicable sections before and after the applicable section. If the ratio of missing values is ac- ceptably low in the tails of the time series, there are no non-applicable sections in the time series. The minimum ratio of available data is 25% in the first k years and last k years of the applicable section, for any k, k = {1,2,···,15}, as well as the minimum ratio is 16.7% for any 30-year subsection of the applicable section. A time series must not contain more than one applicable section (i.e. the applicable section cannot be separated into two parts by a long pause of observation). The minimum length of applicable section is 30 years. 9) The ACMANT has own segments for filling miss- ing data and for substituting outlier values. For this pur- pose spatial interpolation is applied. However, data of non-applicable sections are not treated, and they do not used at all during the homogenisation procedure. 10) Input data-field for ACMANT: Monthly tempera- ture characteristics with monthly time resolution. The lengths of time series may be different, but the data- fields of each series are required to be converted into a common format (which format includes the same number of data for each temperature series) in a way that missing values are filled with –999.9. After the preparation only 4 parameters have to be introduced before application: a) Length of time series, b) First year of time series, c) Number of time series in the network, d) Identifier of network. 11) The result of homogenisation is a) Timings and sizes of inhomogeneities (IHs) for each series. b) Tim- Copyright © 2011 SciRes. IJG  P. DOMONKOS295 ings of outliers. c) Filled data-gaps caused by missing values or outliers inside the series. d) Homogenised time series. Sizes of IHs are characterised with two variables: a) shift in annual means, b) shift in the amplitude of sea- sonal cycle. 3. Main Functions of ACMANT 3.1. Basic Definitions Before the description of the operation of ACMANT, definitions of some basic statistical concepts are pre- sented. Time average of series X (denoted with upper stroke): 1 1n i i n X (1) Standard deviation of series X: 2 1 1n i i x n X (2) Time average of section [j1, j2] of series X: 2 1 21 1 1 j i ij jj j1, j2 X (3) Note that standard deviation for selected section of time series is defined and denoted with the same logic as section-average by Eqution (3). Derivation of anomaly for station s, year j and month m: ,, ,,,, 1 , 1s n jms jmsim i sm ax x n (4) Missing values are represented with xs,i,m = 0, while n’ stands for the number of available observed values in xs,m in Eqution (4). Note that due to missing values the sim- ple time-average cannot be used in Equation (4). ACMANT counts with anomalies during its whole procedure, only in the last step the climatic means (the second term in the right hand of Equation (4)) are added back to the homogenised anomaly series. Spatial correlation: , 12 ,, , , 1 ,,, 111 gsgs gs gs gs gs nhxhx gh shghsh hhhnh gsgs gs r aa aa nnn gs gsgs gs g hn,hxs hn,hx AA hn (5) In Equation (5) g and s denote stations, h is the serial number of month from the beginning of time series (here time has one dimension only), hngs, hxgs and n’gs denote the first month, the last months and total number of months, for which observed data exist in both series, respectively. Missing values of Ag and As are represented with 0 in Equation (5). 3.2. Filling the Gaps of Time Series This operation can be considered as one step of the preparation of time series, because further segments of ACMANT require continuous data series. However, on the other hand, this operation is part of the ACMANT, and it is performed automatically. The interpolation for a missing value of month h in the candidate series (Ag) relies on the same date values of surrounding stations. All the time series of minimum 0.4 spatial correlation with the candidate series are used in the interpolation, if they have observed value for month h. The interpolated value is a weighted average of the anomalies of the partner time series in h. For this inter- polation, section-anomalies (a[h1,h2]) are calculated for the symmetric window (h1,h2] around h. The number of ob- served values used (n’) is usually 100 or 101, i.e. the procedure search h1 and h2 for which h2 – h = h – h1, and n’ε [100,101]. However, when the window is 2 × 10 years wide, i.e. h2 – h1 = 240 and n’ is still smaller than 100, n’ε [30,99] is accepted. In case of h2 – h1 = 240, and n’ < 30, the window-width widens further, and it stops when n’ε [100,101], or when h2 – h1 = 360. Equation (6) shows the calculation of section-anomalies for series s. 2 1 , ,1,2 1 ' h , h shh h ih aa n si a (6) Missing values of As are represented with zero in Equation (6). The interpolated value is the weighted average anom- aly of N* surrounding series which is added to the pe- riod-average of Ag. The weights are the squared spatial correlations. When the sum of squared correlations is lower than a fixed threshold (0.64), zero anomaly ag,h[h1,h2] = 0 is presumed with a certain or entire weight, according to Equations (7) and (8). 2 1 *2 ,, ,1,2 1 11 ' h N , hgs shh h si ara pn gi h a , (7) *2 , 1 max 0.64, N s s p r (8) The gap-filling has to be accomplished before the other steps in ACMANT. However, the first estimations are not final, after some steps of pre-homogenisation the interpolation is repeated in the same way as it is pre- sented here, but with the use of data of higher quality. There is one difference in the second round of the inter- Copyright © 2011 SciRes. IJG  P. DOMONKOS 296 polation process, namely n’ < 100 (more exactly: n’ε [30,99]) for window (h1,h2] is expected only when h2 – h1 = 360. 3.3. Constructing Relative Time Series 3.3.1. General Rules of Constructing Relative Time Series in ACMANT ACMANT makes relative homogenisation which relies on the spatial comparison of time series. The way of this comparison basically follows the traditional rules intro- duced by [20], and applied later widely [21,23]. The relative time series are the arithmetical differences of the candidate series, and the so-called reference series (F) (Equation 9). 12 12 g,q j,jgj,j TAF (9) In Equation (9) a section is defined for which the rela- tive time series is calculated. This section cannot stretch out the ends of any reference-composites, or the ends of the candidate series. Reference series are built from the composition of neighbouring series around the candidate series. The weights of individual composites depend on the spatial correlations between first difference (increment) series. In studies about homogenisation methods one can find different recommendations about the usefulness of first difference series, and about the optimal number of refer- ence-components. For ACMANT the use of first differ- ence series was selected (Equation (10)) for evaluating spatial correlations, because possible large IHs might affect more seriously the spatial correlations of raw time series (R’), than the spatial correlations of first difference series (R). ,,1, hsh s aa a h for (10) 1, 121 s hn Spatial correlations for ∆A are calculated according to Equation (5) with the only difference from that, that at this stage there are no missing values in the series, thus instead of n’ the length of the period examined must be applied. Denoting with bg,s,h the product of ∆ag,h and ∆as,h, the equation can be written in a simpler form (Equation (11)). , ,gs r sgsgsgs gsgs gs gsgs gs gshn ,hxghn ,hxshn ,hx ghn,hxshn ,hx BAA AA (11) For determining the number of reference-components (S), minimum thresholds for acceptable spatial correla- tions are introduced. In the present version of ACMANT this threshold is relatively low, generally r ≥ 0.4, al- though for at least two of the components it has to be at least 0.5. The application of the relatively low threshold values relies on the outcome of some experiments ac- cording to the use of a large number of reference com- ponents usually results in good verification results, even if the spatial correlations of some components are rela- tively low. Its explanation is that the increase of refer- ence components tends to reduce the mean effect of IHs and noise in the reference components. The acceptable minimum of S is 2, in the reverse case homogenisation cannot be fulfilled with ACMANT. Note that one pre-selected time series is often excluded from the reference composites, it is because during the pre- homogenisation the candidate series for which the pre- homogenised reference composites will be used must not be taken into account in any form to avoid non-desired effects of a multiplied use of the same information for the same pieces of data in the homogenisation procedure. For this reason it may occur that the number of reference composites is not more than 1. The composition of reference series for a predeter- mined section [j1,j2] of series Ag is presented by Equation (12). 2 , 1 S gs s g r w 12 12 12 sj,j gj,j j,j A F (12) In Equation (12) w stands for the total weight of the reference composites that have acceptable spatial corre- lation with the candidate series, and available data in section [j1,j2] as well (Equation (13)). 2 , 1 S s g s w 12 j,jr (13) 3.3.2. Application of Homogenisation-Adjustment for Components of Relative Time Series When relative time series are created, the candidate se- ries are always raw or outlier-filtered time series and homogenisation-adjustments have not been applied ear- lier for them, while for reference-composites, homog- enisation-adjustments are usually applied if adjustment factors are available for them at the contemporary phase of the procedure. Note that in the description of the algo- rithm (Sect. 4), certain deviations from these rules will be mentioned. 3.3.3. Constructing Different Relative Time Series for Different Sections of the Candidate Series For sections of the candidate series distinct reference series are often built when the number of available series with adequately high spatial correlation is larger for a section, than for the entire series. In this way usually more than one relative time series are produced for one candidate series. Considering that more than one relative time series Copyright © 2011 SciRes. IJG  P. DOMONKOS297 1,1 can be constructed for one candidate series, we apply an index (q) for denoting the individual reference series for the same candidate series, while index g will be omitted hereafter (since the candidate series is fixed in this ex- amination). Generally Q reference series belong to one candidate series, they starts at year y1,1, y2,1,…yQ,1, while their last years are y1,2, y2,2,…yQ,2. Note that the minimum length of reference series (yq,2 – yq,1 +1) is 30 years, and as reference series never extend over the borders of their candidate series, Y also marks the borders of relative time series. The determination of the set of reference series has four main phases. In phase 1 three time series are deter- mined, 1) the one with the highest w (Fopt) 2) the one with the earliest yq,1 (y1,1) and iii) the one with the latest yq,2. Note that Fopt may have the earliest yq,1 and/or the latest yq,2, thus the final number of reference series originated from this phase can be lower than 3. In phase 2 potential reference series are examined whose starting year (yq,1) is after y1,1, but earlier than yopt,1. Obviously, when yopt,1 – y1,1 < 2 , this phase is omitted. During this examination each possible yq,1 is examined, proceeding step-by-step from y1,1+1 until yopt,1 – 1. Two parameters (p1 and p2) are monitored during this exami- nation (Equations (14) and (15)). 1,1qq py y (14) 2 1 q q w pw (15) A new reference series is selected when 1) p2 ≥ 1.3, or 2) p1 ≥ 5 and p2 ≥ 1.1, or 3) p1 ≥ 10 and p2 ≥ 1.03, or 4) p1 = 30. Once a reference series is selected, the examina- tions are continued recursively by examining the poten- tial starting years between yq,1 and yopt,1. It follows from the written rules that a new reference series is selected with 30 years distance in the starting years at latest. However, when the selection is based on condition 4) (p1 = 30), two special cases need more detailed description,: i) It may occur that the available reference composites for yq–1,1+30 are the same as for yq–1,1. In this case, al- though there is no new reference series, the procedure continues with the virtual yq,1 that equals with yq–1,1+30. ii) Although w usually increases between y1,1 and yopt,1, p2 of lower than 1 may occur for a 30-year subsection. In this case, the maximal p2 is searched for between yq–1,1+1 and yq–1,1+30, and the corresponding reference series is selected. Especially, it may occur (very rarely for ob- served climatic time series) that even the maximal p2 does not satisfy the minimum conditions for creating reference series, and a discrete subsection of [yq–1,1+30, yopt,1] cannot be subdued to homogenisation, meanwhile other sections before and after that subsection can be. In phase 3 the symmetric procedure is applied for po- tential reference series with ending years between yopt,2 and yq(latest),2 than in phase 2, proceeding backwards, step-by-step from yq(latest),2 – 1 until yopt,2 + 1. In phase 4 the selected reference series are ordered according to w, and multiple selections of the same ref- erence series are excluded. 3.3.4. Unified Relative Time Series We introduce the concept of unified relative time series (T+). It will be used for calculating temporary corrections and filtering outliers in the section of pre-homogenisa- tion. T+ is a combination of Tq series. The reasoning of its introduction is empirical, i.e. adjustment factors that are derived from different relative time series, often re- sult in relatively large artificial biases in the low fre- quency variability of the adjusted time series, even if the individual estimations of change-point effects are rela- tively good. The concept of the unified relative time se- ries exploits the fact, that a relative time series can be modified with an arbitrary constant without any effect on the estimation of adjustment factors. The set of relative time series is ordered according to the decreasing values of w belonging to the relevant ref- erence series, then the T series are examined one-by-one following this order. The values of T+ for year j are de- termined when the condition of Tq includes tq,j is satisfied first. In the calculation of values for T+ the relevant val- ues of Tq are usually adjusted with the mean difference between T+ and Tq according to Equations (16)-(18). When j lies before the section(s) for which T+ has values determined from the previously examined T series, Equation (16) is applied, while Equation (17) is applied in the opposite case. * 1 * 1 1 ,, 1Yp qji qi iY tt tt p (16) * 2 * 2 ,, 1 1Y qji qi iY p tt tt p (17) where * 11,1 2,11,1 * 21,22,2 min,, , max,, , q q Yyyy Yyyy 1,2 (18) Notes: 1. Month-indexes for t and t+ are omitted from Equa- tions 16 and 17, first for simplicity, and secondly be- cause often some annual characteristics are used in the homogenisation procedure instead of monthly values (see Sect. 3.4.1). 2. Value p is preset before the calculation of unified Copyright © 2011 SciRes. IJG  P. DOMONKOS 298 time series. The value is relatively low (p = 5) in the be- ginning of the homogenisation procedure, but with the advance of the homogenisation it is higher (up to 30). The philosophy of limiting p stems from the fact that unadjusted change-points may affect the apparent dif- ference of T+ and Tq, therefore sections that are relatively close to the newly determined values are used only. For the very same reason p is lower in the beginning of the homogenisation procedure, and with the decreasing in- fluence of unadjusted change-points p increases. 3. The p applied can be lower than its predefined value when the number of available value-pairs of T+ and Tq is lower than the predefined value of p. When the number of applicable p is lower than 3, adjustment is not made, i.e. in this case tj + = tq,j. It is always the case for q = 1. 4. It is seldom, but may occur that previously deter- mined values of T+ exist on both sides of the newly de- termined values. Introducing Y1 ’ for the starting year of the right section and Y2 ’ for the ending year of the left section, and substituting Y1 * and Y2 * in Equations (16) and (17) with them, the estimations of the adjustment factors included in the referred formulas are calculated first and they are denoted with E1 and E2, respectively. Then a linear transition between E2 and E1 provides the adjustment factors for the values between Y2 ’ and Y1 ’ (Equation (19)). 12 ,2 1 12 12 jqj Yj jY tt EE YY YY (19) 3.4. Detecting IHs with the Main Detection 3.4.1. Detection Process In the Main Detection the timings and sizes of IHs are searched with fitting step-functions to two variables, namely to the annual means (TM) and summer-winter differences (TD) in relative time series (Equations (20) and (21)). In the following description the index q of relative time series is omitted. 12 , 1 12 m m j t tm (20) ,5,6,7,8 ,11 ,12,1,2 0.5 0.5 3.5 jjjj jjj j ttttt ttt td (21) In Equation (21) the second index represents calendar month. Solutions with common timings of steps are consid- ered only, and the minimum sum of squared errors is searched in a similar way as it is described by [24], [9], etc. (Equations (22) and (23)). 1 12 '22 2 0 [ ,,...]01 min k Kk j K ii jj jkij tmc td kk TMTD (22) 00j , (23) 1K j L L denotes the length of the period examined, in years, c0 is constant, while the number of change-points for the selected period is K’. k characterises not only the serial number of change-points, but the serial number of sec- tions between adjacent change-points too (Equation (24)). kk1 kj1,j TM TM (24) c0 represents the estimated significance of changes of TD in comparison to that of TM in relative time series. In its estimation not only the mean sizes, but the sig- nal/noise rate also had to be taken into account. In the present application c0 = 2–0.5. For selecting the most appropriate K’, the Caussinus – Lyazrhi criterion [25] is applied (Equations (25) and (26)). 22 2 10 0 22 2 0 1 ()()( ) ln 1 ()() K kk k L ii i jj c tmc td G kk TMTMTD TD TM TD (25) 2' ln 1 K G L L (26) The Main Detection differs in two points from the classic Caussinus-Mestre detection method: 1) Step functions are fitted to two variables, 2) The minimum distance between two change-points is 3 time-units: 13 kk jj (27) '0 Kkk 3.4.2. Selection of Relative Time Series Q different relative time series (T1, T2, ···,TQ) are derived for one candidate series, and they are ordered according to the sum of squared correlations of the refer- ence-composites (w1 > w2 >… wQ). Each of them is used in the Main Detection, but frequently some sections of the relative time series are used only. The algorithm of the relative time series selection is as follows: 1) First the T1 series is used with its whole length. In this step section [y1,1,y1,2] of the candidate series is ho- mogenised. 2) When the first q relative time series has already been used, Tq+1 is applied for sections that a) lie within [yq+1,1,yq+1,2] and b) have not been homogenised with the first q relative time series. 3) When Tq+1 is applied, the tails of the sections ho- Copyright © 2011 SciRes. IJG  P. DOMONKOS299 1 1 mogenised with the previous T series are often over- lapped. It means that when ag,e1 belongs to a section that has been homogenised previously, but ag,e1-1 has not, and e1 > yq+1,1, a d1-year long section after e1 – 1 is subdued again homogenisation. The usual length of this overlap is 9 years, but an overlapping section is not allowed to ex- tend over a) IHs detected in previous steps, b) ends of Tq+1 (i.e. yq+1,1 and yq+1,2). Let the first IH after e1 be de- noted by k1 then the length of overlap is determined by Equation (28). 1111,2 min9, 1,1 q dkeye (28) For tails that lie in the other ends of the previously homogenised sections (i.e. whose last point is e2), the overlap (d2) is calculated with the same logic (Equation (29)). 22221, min9, ,1 q dekey (29) In Equation (29) k2 stands for the first IH before e2. 3.5. Secondary Detection In the Secondary Detection short-term IHs are searched in relative time series adjusted according to the results of the Main Detection. This operation is performed only when the maximum of accumulated anomalies in ad- justed relative time series exceeds some predefined thresholds. Adjusted relative time series and the timing of the maximum of accumulated anomalies are denoted with T* and H*, respectively. T* is examined in its monthly resolution, and the section that is selected around H* is not allowed to be longer than 60 months. This section has two sub-sections, namely the search of the maximum of accumulated anomalies and the de- tection of IHs around H*. 3.5.1. Search of the Maximum of Accumulated Anomalies 5-month and 10-month moving averages are calculated for the normalised anomalies of Tq*. All the relative time series of the candidate series are used (q = 1,2,···,Q). In Equations (30) and (31) the calculation of accumulated anomalies is shown for 5-month and 10-month periods, respectively. ** 2, ,* 2 1 MA 55() hqh qh ih t b q q T T (30) ** 4, ,* 5 1 MA10 10 () hqh qh ih t b q q T T (31) Note that in Equations (30) and (31) i is not allowed to be lower than 1 or higher than the number of months (nm) * h ≤ nm – 4 have to be satisfied for Equations (30) and (31), respectively. After having the in Tq, therefore the conditions of 3 ≤ h ≤ nm – 2 and 6 ≤ accumulated anomalies (MA5(b) and M 3.2. Detection of IHs around the Maximum of 1) Selection of relative time series nd for that operation av H h1,h2] of 60 months le A10(b)) for each Tq*, their maximums are determined. The maximums are calculated without sorting the accu- mulated anomalies according to q, and in this way only two maximal values are obtained, one for MA5 and an- other for MA10. In the present version, Secondary De- tection is made only when max(MA5(b)) ≥ 2.0 or max(MA10(b)) ≥ 1.4. When exists a H* for which the former relation is satisfied, the timing of the maximum of 5-month anomalies is used, while the timing of the maximum of 10-month anomalies is used when only the latter relation is satisfied. 5. Accumulated Anomalies A window is edited around H* a ailable data are needed in both sides of H*. Usually the Tq* of the highest w is used for which at least 20 data are available in each side of H*. When non of the Tq* series meet with this condition (because H* is close to one end of the candidate series), all the Tq* series are examined again, with less strict conditions. In the second round the expected minimum of available data (in each side of H*) is 10, and in the third round (if that is necessary) the minimum threshold is 2 only. 2) Edition of window around* Usually a symmetric window [ ngth is edited around H*, but the window must not overlap IHs detected in earlier steps or any end of the Tq series, therefore it can be narrower than 60 months. Let suppose that K1 change-points has been detected in the earlier steps of the homogenisation procedure for section [1,H*] of the series, then the borders of the window are determined by Equations (32) and (33). 1 11, 1 K * max 29,hHH (32) 1 * 21 min30, , K hHHn m (33) 3) Detection of IHs in windows s is again the Caussi- nu stant sections are substituted with harmonic fu The base of the detection proces s-Mestre method. However, in the Secondary Detec- tion the constant sections of step-function are substituted with harmonic functions of annual cycle for sections of longer than 9 months, and some other modifications also exist relative to the original Caussinus-Mestre method. The list of differences from the original method is as follows. a) Con nction of annual cycle for sections longer than nine Copyright © 2011 SciRes. IJG  P. DOMONKOS 300 minimum distance between two change-points is are allowed to be de- te on (34) is ap- pl months; b) The 3 time-units, i.e. 3 months in this case, but Equation (26) is applicable here otherwise; c) Maximum two change-points cted in a window [h1,h2]. (K’ = 0, 1 or 2) Describing more detailed point i), Equati ied for fitting harmonic function of annual cycle. 1 2π2πmm sin cos 12 12 1, hkkAB kk uc c hH H , (34) cA and cB are general constants in the procedure, because se of β’ = 0 the function is constant and this fact sh .6. Calculation of Adjustment Factors .6.1. ANOVA f IHs of individual time series makes it NT the ANOVA operates within an auto- m the ANOVA is applied separately for tw .6.2. Homogenisation-Adjustments during the After IHs identified, adjustment- used for cal- cu they characterise the relation between the phase of the annual cycle and calendar month. Their values are set to have the modus of the harmonic functions at the solstices (cA = –0.1031, cB = –0.9947). Between two adjacent change-points, αk’ and βk’ are also constants, and their most proper values are searched with iteration. For find- ing the best fitting model (K’, as well as the most appli- cable timings of change-points), the function fitting of Equation (34) must be applied for each subperiod of the examined window, then the model with the lowest Caussinus—Lyazrhi score is selected. This operation contains large number of calculations, but by applying an economic algorithm, the computation time is kept fairly short. In ca ows that the step-function is a special case of the func- tion family applied here. 3 3 The interaction o necessary to calculate the precise adjustment-terms by an equation system. In ACMANT the ANOVA method is applied. In brief, the application of ANOVA to calculate adjustment-terms for correcting IHs, is based on the di- vision of observed time series to three components, namely to climate effect, stations effect (IH) and noise. In [9] it is proved that the optimal estimation of adjust- ment-terms is provided when the noise term is set to be zero in the equation system, thus the ANOVA provides the optimal estimation of adjustment-terms. The referred study also contains the detailed description of the appli- cation of ANOVA in the homogenisation of climatic time series. In ACMA atic procedure, therefore a special attention is needed to treat cases when the equation system has no determi- nistic solution. It could occur when all the time series of a network (those that are comparable in the homogenisa- tion procedure) have a change-point in the same time. In that case the behaviour of sections before and after the common change-point is independent. To avoid this case the smallest IH is cancelled if all time series show IH at the same time. In ACMANT o annual variables (i.e. for TM and TD), then the monthly correction-terms are derived from them (see Sect. 3.6.3). The ANOVA is applied after the Main De- tection, then it is repeated after the Secondary Detection, and if the number of IHs is reduced at the end of the procedure relying on posterior tests, the application of ANOVA is repeated again. However, ANOVA is not applied during the pre-homogenisation, because it is not a tool for making step-by-step improvements in the dataset. 3 Pre-Homogenisation having the timings of terms for executing homogenisation can be deduced di- rectly from relative time series. Although a part of the detected biases can be caused by the impreciseness of reference series, adjustment-terms are always applied with its full content to the candidate series. The unified relative time series (T+) are lating temporary adjustments. Let suppose that for IH k* Equations (35) and (36) show the shifts in TM and TD. **k k1 k TMTM * (35) **k k1k TDTD * (36) If the number of detected IHs is K, the c fe umulated ef- ct of IHs on the candidate series in year i, i ≤ k* is characterised by Equations (37) and (38). K TM TM * i kk k1k (37) * K i kk k1 k TDTD (38) .6.3. Derivation of Monthly Correction-Terms U de- 3 If IH k* has the timing H(k*) in monthly scale and notes the adjustment-term, it can be given for any year i and month m within the period [H(k*-1)+1,H(k*)] by Equation (39). Corrections from β are distributed among the calendar months in a way that the annual cycle is a harmonic function with its extreme values in the solstices, and the degree of changes in td satisfies Equation (21). These conditions determine the monthly constants (cm) in Equation (39). Copyright © 2011 SciRes. IJG  P. DOMONKOS301 c , * K imkm k kk u (39) 3.7. Outlier-Filtering Outlier filtering is applied two times in ACMANT, namely for raw time series first, then after some steps of the pre-homogenisation it is applied again. The applied method is the same in both cases, only one little differ- ence will be mentioned below. Two operations are performed in this step. 1) Anomalies with higher than 4 standard deviations are filtered according to Equation (40). ,, 4 sqh t s,q s,q TT (40) For each series s and month h always the Ts,q of the highest w is selected which contains h. Note that in the first outlier-filtering the mean of Ts,q is considered to be 0, because for differences of raw anomaly series the ex- pected value is 0. 2) If in a 10-month long period, more than one outliers of the same sign occur according to i), a confirmation is needed, because the accumulation of seeming outliers might be caused by large long-term variability. Therefore in this case a second operation is accomplished, in which potential outliers are examined with the statistical prop- erties of the time-neighbourhood. Nineteen-month long windows are used for this purpose. The potential outlier is confirmed when the deviation from the win- dow-average is larger than 3.5 standard deviation of the values within the window, but is not considered to be outlier in the reverse case (Equation (41)). For this op- eration, again the relative time series of the highest w, but with available data around h is selected. ,3.5 qh t q h9,h9q h9,h9 TT (41) Note that when the number of available data is less than 9 in one side of the window, this calculation is made in a narrower window. In this case, if another Ts,q series (of lower w) contains data for a full-size window, the calculation is repeated with that data, and the results are overwritten by that. 4. The Algorithm of ACMANT Homogenisation Method After the main functions of ACMANT have been de- scribed, in this section the operation of the whole proce- dure is presented. In the homogenisation procedure raw time series are converted several times (by interpolation, outlier-filtering, pre-homogenisation), thus they go through several stages before achieving their final form. During the procedure some earlier stages are preserved, and reused. To make distinctions among different stages of the same series stage-codes are introduced. The code of raw time series is 0, and if the series does not have sufficient spatial cor- relations with other time series it might remain un- changed during the homogenisation procedure of the network. However, the gap-filling is done even for these series, thus the code 0 indicates raw but continuous time series. The meaning of the codes: 0 – raw 1 – outlier-filtered 2 – two times outlier-filtered 3 – pre-homogenised without outlier filtering 4 – pre-homogenised and outlier-filtered 4a – one time series is excluded during the pre-homogenisation 5 – pre-homogenised and two times outlier filtered 5a – one time series is excluded during the pre-ho- mogenisation 6 – homogenised The algorithm of ACMANT Part I: Preparation 1. Calculation of anomalies (Equation (4)). 2. Calculation of spatial correlations (Equation (5)). 3. Filling of data gaps in each time series (Sect. 3.2). The results are the series of code 0. 4. Calculation of first difference series (Equation (10)) and their spatial correlations (Equation (11)). 5. Creation of relative time series from series-0 (Sects. 3.3.1 and 3.3.3). 6. Outlier-filtering for each time series (Sect. 3.7), the results are series-1. 7. Spatial correlations are recalculated from series-1. 8. Interpolation for substituting outliers for each time series (Sect. 3.2). When an outlier was detected in a se- ries g in the same year and month at which interpolation occurred in another series (s ≠ g) at step 3, its value is re-interpolated at this step. Part II: Pre-homogenisation 1) Calculation of first difference series and their spa- tial correlations from series-1. 2) Creation of relative time series (Sects. 3.3.1, 3.3.3) and unified relative time series (in Sect. 3.3.4 in Equa- tions 16 and 17 p = 5). Type of candidate series: 1. Type of reference components: 1. 3) Use of the Main Detection (Sect. 3.4) for ranking time series according to the degree of inhomogeneous character. Let the timings of IH (k) be denoted by jk, the mean estimated bias of [jk+1,jk+1] by uk’, then an indica- tor (z) of the degree of inhomogeneous character for sec- tion [jk1+1,jk2] is calculated by Equation (42). Copyright © 2011 SciRes. IJG  P. DOMONKOS 302 2 1 2 1 1.2 21 1 k kk kk kk jju z jj (42) Maximums of z values are searched examining each possible k1 – k2 pair (0 ≤ k1 ≤ k2 ≤ K), then time series are ordered according to their maximal z values. The actual form of Equation 42 was chosen after some experiments regarding the efficiency achievable. – In this step multi- ple relative time series are used for determining the tim- ings of IHs (as usual), but the T+ is used for calculating indicator z. Steps 4 - 7. compose a block that is accomplished for each series in the order determined in step 3. 4) Calculation of relative time series. Type of candi- date series: 1. Type of reference composites: 4a when the composite has already bean pre-homogenised, 1 other- wise. 5) Main Detection. 6) Calculation of relative time series and T+ with the exclusion of one of the possible composites, p = 10. Type of candidate series: 1. Type of reference compos- ites: 4 when the composite has already been homoge- nised, 1 otherwise. 7) Homogeneity-adjustments (Sects. 3.6.2 and 3.6.3). a) Input: series-0, adjustment-terms: from T+ of step 3, type of results series: 3; b) Input: series-1, adjust- ment-terms: from T+ of step 3, type of results series: 4; c) Input: series-1, adjustment-terms: from T+ of step 6, type of results series: 4a. 8) Calculation of first difference series and their spa- tial correlations from series-4. 9) Calculation of relative time series. This step pre- pares the repetition of outlier-filtering, and for this rea- son the candidate series are without previous out- lier-filtering. Type of candidate series: 3. Type of refer- ence composites: 4. 10) Outlier-filtering. The results are series-5. 11) Calculation of spatial correlations from series-5. 12) Recalculation of interpolated values using series-4. The primer results are series-5. Then from the interpo- lated values the homogenisation-adjustments are sub- tracted, and with these values the outliers in series-0 are substituted. The results are series-2. 13) Calculation of relative time series and T+ with the exclusion of one of the possible composites, p = 30. Type of candidate series: 2. Type of reference compos- ites: 5. 14) Homogenisation-adjustments (Sects. 3.6.2 and 3.6.3). Input: series-2, adjustment-terms: from T+ of step 13, type of result series: 5a. Part III: Homogenisation Note: In this part unified relative time series are not used. 1) Calculation of relative time series. Type of candi- date series: 2. Type of reference composites: 5a. 2) Main Detection. 3) Exclusion of one IH, if there occurs a common timing of IHs for all time series. Then the least signifi- cant IH is selected, based on the calculations of indicator z* around the timings of the common IH (k), Eqution (43). 222 11 0 *kkkk zjj c (43) In Equation (43) αk and βk are determined with Equa- tions (35) and (36). The smallest z* indicates the least significant IH, then that is excluded from the list of de- tected IHs. 4) Refining timings of IHs in monthly time scale. In the Main detection annual characteristics are used only, so the timings of IHs cannot be assessed with monthly preciseness from that. Here, the relative time series (T) of step 1 are used in monthly resolution. – The first esti- mation for the timing of IH k is taken from step 2, and it is the December of the year (j) detected. Then two-phase harmonic functions are fitted in a 48-month wide win- dow centred at December of year j. This fitting is made in the same way as for the Secondary Detection (Eqution (34)), but here the number of change-points is fixed to be 1 within the window. Further limitation is that the timing of the change-point is searched up to 12 months distance from the centre of the window. – For the calculations of this step always the Tq of the highest w is selected that contains the 48-month window around jk. 5) Calculation of correction-terms with ANOVA. In- put field: series-2 and timings of IHs from steps 2-4. This step consists of three operations: a) ANOVA for correc- tion-terms in annual means (TM) (Sect. 3.6.1); b) ANOVA for correction-terms in summer-winter differ- ences (TD) (Sect. 3.6.1); c) Calculation of monthly cor- rection-terms (Sect. 3.6.3). – In ACMANT the input variables are introduced to ANOVA in monthly resolu- tion, as at this phase of the procedure the timings of IHs are available with monthly preciseness. Problems do not occur in calculating α, since the calendar months are nearly evenly distributed between any two adjacent change-points. By contrast, the summer-winter differ- ence is a characteristic which has no values in monthly time-scale. The problem is tackled by applying moving weighted averages of monthly anomalies, providing monthly values in this way for ANOVA calculations (Equation (44)). *5 ,66 *5 0.5 H mH mHmH mH HH tdc acca H (44) Copyright © 2011 SciRes. IJG  P. DOMONKOS303 1 k Examining Equation (44) it can be seen that TD’ characterises the summer-winter difference, and it has monthly values. Values for cm’ are set in harmony with Equation (21), (c1’= –1/3.5, c2’= –0.5/3.5, etc.). 6) Application of homogenisation-adjustments on relative time series of step 1. Each Tg,q (q = 1,2,···,Q) is adjusted with the adjustment-factors determined by step 5 for series g. The results are T*. Steps 7 and 8 compose a block whose steps are ful- filled cyclically as long as inner indicators show the ne- cessity of the continuation of the cycle. 7) Calculation of the maximums of accumulated and normalised anomalies in adjusted relative time series. (Sect. 3.5.1). If one of the maximums exceeds the pre-defined thresholds, step 8 follows, otherwise the procedure continues with step 9. 8) Secondary Detection (Sect. 3.5.2). Step 7 follows, but before that the section of time series that has already subdued to Secondary Detection, is excluded from fur- ther examinations of accumulated anomalies. 9) Calculation of correction terms with ANOVA. The only difference relative to step 5 is that here the list of IHs is supplied with the result of the Secondary Detec- tion. 10) Application of correction-terms on series-2. The results are series-6. Part IV. Final adjustments Some IHs might turn out to be insignificant after the ANOVA calculations. They are removed, and the ANOVA is repeated with the rest of the IHs. These steps are fulfilled cyclically as long as there is no insignificant IH after the ANOVA calculations. 1) The significance of each IH (k) is controlled with t-test. The size of IH is characterised by the sum of ab- solute values of αk and c0βk where αk and βk are deter- mined with Equations (35) and (36). The periods to which the shift is assigned are presented by Equations (45) and (46). 1kk lHH (45) 21k lH H (46) The standard deviation for both periods is considered to be the same as the standard deviation of the relative time series in which k was detected. Let the sum of l1 and l2 be denoted by l, then statistic p* can be given by Equation (47). 012 2 *kk clll pl (47) Note that p* differs from regular t-statistics of l-2 freedom because it includes β, while σ characterises the standard deviation of α only. – In the present application, thresholds for selecting significant IHs equal to the regu- lar thresholds (depending on l) for the 0.05 significance level. If at least 1 IH is excluded, step 2 follows, other- wise step 4. 2) Calculation of correction terms with ANOVA. The only difference relative to step 5 of Part III is, that here the list of IHs is altered relative to the previous calcula- tions. 3) Application of correction-terms on series-2. The results are series-6. Step 1 follows. 4) Long-term means of monthly temperatures are added to the homogenised anomalies (Equation (48)). a* marks homogenised anomalies and V stands for ho- mogenised temperature series. * ,, ,,,, 1 , 1s n jms jmsim i sm va x n (48) 5. Verification 5.1. Test-Datasets In the COST HOME action (COST ES0601) a bench- mark dataset with known artificial IHs was built by a group of experts, and was announced [26] for the clima- tological community, for comparing the results of dif- ferent homogenisation methods. This benchmark consists of 40 networks of 100-year long series of simulated monthly temperatures, 40 networks of simulated precipi- tation data and some networks with real observed data. For verification purpose only the simulated temperature data are used in this study, since in datasets of real ob- servations the properties of inhomogeneities are never known perfectly, thus exact verification cannot be per- formed for them. Half of the simulated networks was generated with white noise background (synthetic data), while in the other half of the networks the background noise mimics the low-frequency variability of time series better (sur- rogated data). The benchmark contains networks of 15 time series (25%), networks of 9 time series (25%) and networks of 5 time series (50%). The spatial correlations are high (often higher than 0.8) what is typical for tem- perature networks of the last 100-150 years observations in Europe and the US. The frequency of IHs varies widely, but most networks contain a few large IHs and a lot of small IHs. See more details in [26]. In this study another test dataset is also used. It con- sists of 100 surrogated and 100 synthetic networks of monthly temperature data. This dataset (referred as benchmark-2 hereafter) was created exactly in the same way as the benchmark dataset, the only difference is that in benchmark-2 all the networks contain 9 time series (50%) or 15 time series (50%). Copyright © 2011 SciRes. IJG  P. DOMONKOS 304 5.2. Evaluation of Efficiency The root mean squared error (RMSE) caused by IHs or imperfect homogenisation was calculated for some sta- tistical characteristics of raw time series (WR) and for that of homogenised time series (WH). Then the efficiencies were calculated by Eqution (49). H R WW Eff W (49) The verified characteristics are: 1) RMSE of monthly biases, 2) RMSE of biases in annual means, and 3) RMSE of slope-biases in the linear trend for the entire period of time series. 5.3. Efficiency Results In January of 2010 the first evaluation of efficiencies was presented for the participants of COST event, and some of the results have been published [27]. It was found that the performance of ACMANT is one among the most effective homogenisation methods. However, the author has found problems with the reliability of climatic trend estimation of that version (ACMANTv0), particularly when the method was used for homogenising small net- works (N = 5). After the causes of the bias have been identified, some modifications were made in ACMANT. The present version (ACMANTv1, February, 2011) that is described in this study contains several modifications relative to ACMANTv0. In the ACMANTv0 neither ANOVA, nor unified relative time series were used for calculating correction-terms, but those terms were calcu- lated using the same relative time series as in which the IHs were detected. The lack of harmonisation among individual assessments may cause accumulated biases in the estimation of long term trends. Another change is that in ACMANTv1 the modus of the annual cycle coin- cide with solstices, why in ACMANTv0 they were in mid-January and mid-July. However, in the bench- mark-homogenisation I still used the seasonal cycle of the earlier version, because it provides the best results for the benchmark. The ACMANTv1 produces better results than the ACMANTv0 not only in the trend estimation, but also in the reconstructions of other statistical properties of time series. For the 40 simulated networks of the benchmark the efficiency of trend-slope estimation increased from 0.400 to 0.745, that of the annual mean temperatures increased from 0.516 to 0.661, and that of the monthly mean temperatures increased from 0.434 to 0.553. As since February 2010 I know the true positions of IHs in the benchmark, another test dataset, the bench- mark-2 was used for the verification of ACMANTv1. Surprisingly, the results for benchmark-2 are slightly even better, than the results for the former benchmark (Figure 1). When the values for Figure 1 were calcu- lated, the small networks (N = 5) of the benchmark were excluded, for using test-datasets of the same statistical properties. It can be seen that 1) for relatively large net- works even the ACMANTv0 performed quite well, 2) the ACMANTv1 has always better efficiency than the ACMANTv0, 3) the blind-test results are slightly even better than the results achieved in the benchmark, 4) the results are better when synthetic data are homogenised in comparison with the homogenisation of surrogated net- works, 5) the efficiency in reducing the monthly RMSE is slightly poorer than the reduction of the annual RMSE. The author cannot explain why the efficiency results are better for the benchmark-2 than for the benchmark. The opposite relation should be expected, since the ACMANTv1 contains some semi-empirical parameters which were assumed based on experiments with the benchmark. Perhaps the 20 networks of the benchmark that were used for Figure 1 frequently contain difficult coincidences of IH and noise-terms by accident, in com- parison with the mean properties of the much larger benchmark-2. Anyhow, the achieved performance is out- standingly high. The author does not know other ho- mogenisation method with similar or better efficiency. 6. Discussion and Conclusions The development of ACMANT relies on previous an- alyses of efficiencies of homogenisation methods [28], [29]. Notwithstanding, the application of homogenisation methods on such a complete dataset as the benchmark of the COST HOME offered and offers further opportuni- ties to reveal the efficiency characteristics of methods. This study restricts to discuss characteristics whose im- pacts to the efficiency of ACMANT are unambiguous. Seven favourable characteristics and three still existing shortcomings are discussed: 1) IH-sizes of temperature series usually have seasonal cycle. It is caused by the fact that most of the IHs have relation to the change of radiation-sheltering or other radiation effects, and these effects are larger in summer than in winter. Thus, following the annual cycle of radia- tion intensity, most of temperature IH sizes have quasi-harmonic cycle. The benchmark of COST HOME contains these seasonal changes of IHs rather realistically. The ACMANT applies a bi-variable test for detect IHs, one variable is the annual mean (TM), and the other is the summer - winter difference (TD). This way of detec- tion is very effective, because a) The two variables often have change-points with the same timings, thus the sig- Copyright © 2011 SciRes. IJG 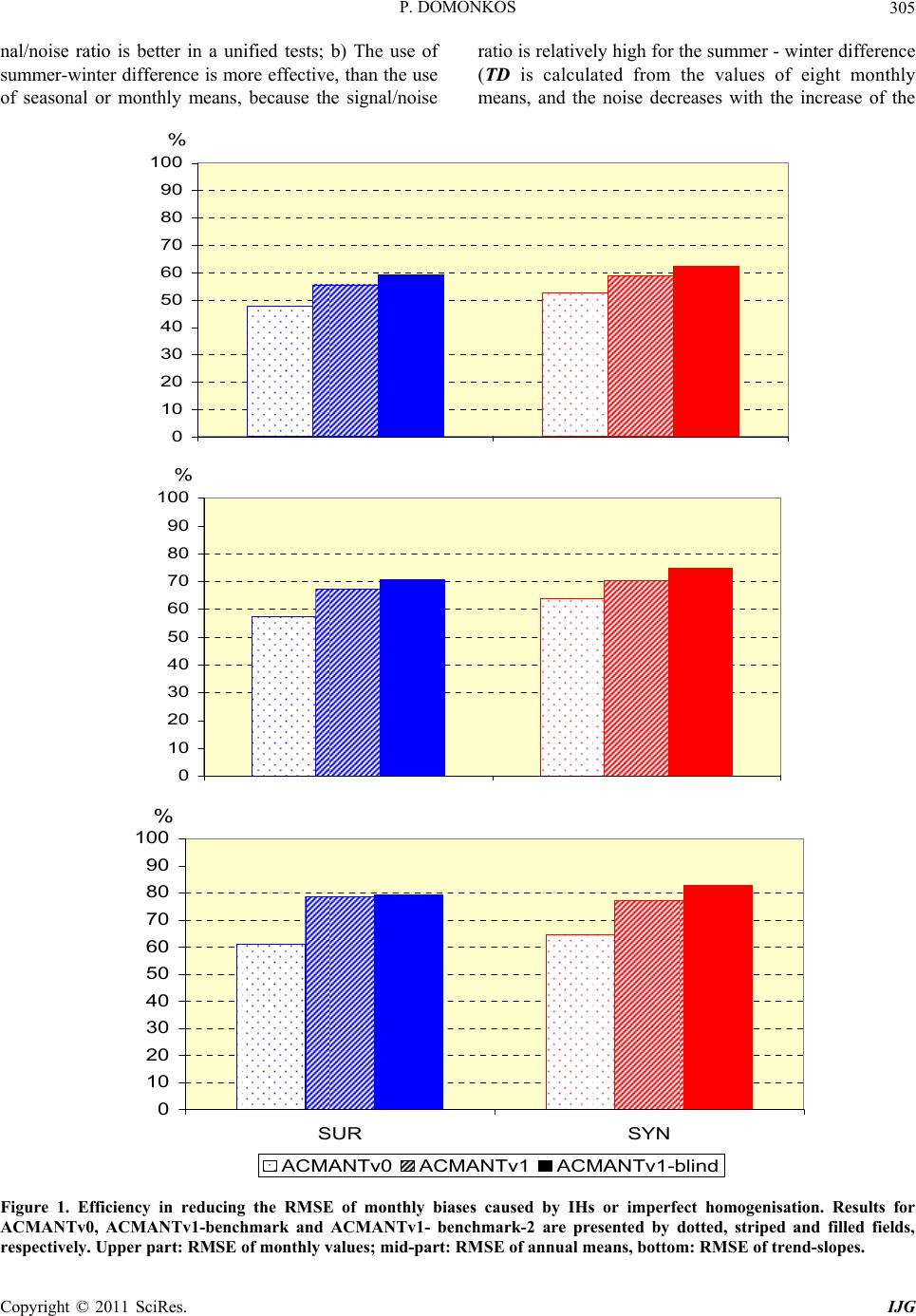 P. DOMONKOS Copyright © 2011 SciRes. IJG 305 nal/noise ratio is better in a unified tests; b) The use of summer-winter difference is more effective, than the use of seasonal or monthly means, because the signal/noise ratio is relatively high for the summer - winter difference (TD is calculated from the values of eight monthly means, and the noise decreases with the increase of the 0 10 20 30 40 50 60 70 80 90 100 % 0 10 20 30 40 50 60 70 80 90 100 % 0 10 20 30 40 50 60 70 80 90 100 SUR SYN % ACMANTv0 ACMANTv1ACMANTv1-blind Figure 1. Efficiency in reducing the RMSE of monthly biases caused by IHs or imperfect homogenisation. Results for ACMANTv0, ACMANTv1-benchmark and ACMANTv1- benchmark-2 are presented by dotted, striped and filled fields, respectively. Upper part: RMSE of monthly values; mid-part: RMSE of annual means, bottom: RMSE of trend-slopes.  P. DOMONKOS Copyright © 2011 SciRes. IJG 306 number of averaged values); c) Distinct analyses of sea- sonal and monthly series may result in set of detected change-points with poor seasonal coherence. In that case, after having the primer results, a harmonisation is neces- sary to obtain a realistic description of IH properties. Considering that that harmonisation needs further esti- mations loaded with uncertainties, it might cause biases in the result. In contrast, when TM and TD are examined, such a harmonisation is unnecessary, because the sea- sonal cycles of IHs can be derived directly from the de- tection result. 2) One base of the development is the Caussinus - Mestre detection method. Verification results show that the Caussinus - Mestre detection method is one of the best among the existing methods [29]. 3) According to some tests fulfilled with the Caussinus - Mestre detection method, its performance has turned out to be better, when detection of IHs with shorter than 3 time units is not allowed. It is likely, because noise can produce IH-shaped changes in the very short time-scale more frequently than in longer time-scale. The ACMANT applies this experience. 4) In ACMANT the ANOVA is applied for calculating corrections which method provides the optimal estima- tions of correction-terms. 5) The pre-homogenisation of reference components is favourable when information specific for the connection between the candidate series and its references is not utilised in that step. The pre-homogenisation included in ACMANT improves the certainty of the estimation of number of IHs and that of the timings of IHs. 6) When the assessment of IH-positions are relatively confident at least for large-size IHs, the applied method for finding the timings of IHs in monthly time-scale gives improvement. Note that according to some ex- periments with the COST-benchmark, the application of the same technique in an earlier phase of the procedure for assessing timings with monthly preciseness did not result in any improvement of efficiency. 7) The calculation of correction-terms with ANOVA may show that some IHs which seemed to be significant in the detection process, do not have significance in the final results. With the exclusion of the insignificant IHs (their percentage was approximately 10% when the COST-benchmark was used) a better estimation of cor- rection-terms can be provided basing on the significant IHs only. Three shortcomings still wait for the application of further developments. 1) The aim of the Secondary Detection is to identify short-term but large-size IHs. However, as it operates after the Main Detection, a) the results of the Main De- tection have errors due to unfiltered large-size, short- term IHs, b) the results of the Secondary Detection are affected by the errors of earlier steps. 2) The ACMANT is a purely statistical procedure, now it is impossible to use metadata (documental infor- mation of technical or environmental changes in the ob- servation) information within ACMANT. However, the author thinks that the potential usability of metadata is limited when the spatial density and spatial correlations of data is appropriate to perform statistical homogenisa- tion, since metadata do usually not contain quantitative information about the degree of local effects. 3) The present method is applicable for monthly tem- peratures from mid- or high-latitudes, and is not applica- ble for other climatic variables. The ACMANT contains innovations whose application would likely be useful for homogenising other variables than monthly temperatures, therefore further developments of homogenisation me- thods are needed. A task for the future is, to apply efficiency-tests of wider properties of time series and data networks than which are provided by the COST-benchmark. The para- meterisation of ACMANT has to be checked or modified relying on further tests. Summarising, the ACMANT is a new homogenisation method which has been developed for homogenising mid- and high-latitude temperature series of observing networks. It has outstanding efficiency among statistical homogenisation methods. Its use is particularly recom- mended for homogenising networks comprising large number of time series with sufficient spatial correlations, since the ACMANT is a fully automatic method. The executable file of ACMANTv1 together with its user-guide is freely downloadable from http://www.c3.urv.cat/members/pdomonkos.html. 7. Acknowledgements The research was funded by the COST ES0601 project and by the Centre for Climate Change (C3) of University Rovira i Virgili. The author thanks Victor Venema for providing access to dataset benchmark-2. 8. References [1] T. A. Buishand, “Some Methods for Testing the Homo- geneity of Rainfall Records,” Journal of Hydrology, Vol. 58, No. 1-2, 1982, pp. 11-27. doi:10.1016/0022-1694(82)90066-X [2] H. B. Mann and D. R. Whitney, “On a Test of Whether One of Two Random Variables is Stochastically Larger than the other,” The Annals of Mathematical Statistics, Vol. 18, No. 1, 1947, pp. 50-60. doi:10.1214/aoms/1177730491 [3] J. R. Lanzante, “Resistant, Robust and Non-Parametric  P. DOMONKOS307 Techniques for the Analysis of Climate Data: Theory and Examples, Including Applications to Historical Ra- diosonde Stationdata,” International Journal of Clima- tology, Vol. 16, No. 11, 1996, pp. 1197-1226. doi:10.1002/(SICI)1097-0088(199611)16:11<1197::AID- JOC89>3.0.CO;2-L [4] A. R. Solow, “Testing for Climate Change: An Applica- tion of the Two-Phase Regression Model,” Journal of Climate and Applied Meteorology, Vol. 26, No. 10, 1987, pp. 1401-1405. doi:10.1175/1520-0450(1987)026<1401:TFCCAA>2.0.C O;2 [5] L. A. Vincent, “A Technique for the Identification of Inhomogeneities in Canadian Temperature Series,” Journal of Climate, Vol. 11, No. 5, 1998, pp. 1094-1104. doi:10.1175/1520-0442(1998)011<1094:ATFTIO>2.0.C O;2 [6] H. Alexandersson, “A Homogeneity Test Applied to Pre- cipitation Data,” Journal of Climatology, Vol. 6, No. 6, 1986, pp. 661-675. doi:10.1002/joc.3370060607 [7] X. L. Wang, Q. H. Wen and Y. Wu, “Penalized Maximal t Test for Detecting Undocumented Mean Change in Climate Data Series,” Journal of Applied Meteorology and Climatology, Vol. 46, No. 6, 2007, pp. 916-931. doi:10.1175/JAM2504.1 [8] T. Szentimrey, “Multiple Analysis of Series for Homog- enization (MASH),” Second Seminar for Homogenization of Surface Climatological Data, WMO, Geneva, 1999, pp. 27-46. [9] H. Caussinus and O. Mestre, “Detection and Correction of Artificial Shifts in Climate Series,” Journal of Royal Statistics Society Series C, Vol. 53, No. 3, 2004, pp. 405-425. doi:10.1111/j.1467-9876.2004.05155.x [10] T. C. Peterson and 20 co-authors, “Homogeneity Ad- justments of in Situ Atmospheric Climate Data: A Re- view,” International Journal of Climatology, Vol. 18, No. 13, 1998, pp. 1493-1517. doi:10.1002/(SICI)1097-0088(19981115)18:13<1493::AI D-JOC329>3.0.CO;2-T [11] E. Aguilar, I. Auer, M. Brunet, T. C. Peterson and J. Wieringa, “WMO Guidelines on Climate Metadata and Homogenization,” WMO, Geneva, 2003. [12] J.-F. Ducré-Robitaille, L. A. Vincent and G. Boulet, “Comparison of Techniques for Detection of Discontinui- ties in Temperature Series,” International Journal of Climatology, Vol. 23, No. 9, 2003, pp. 1087-1101. doi:10.1002/joc.924 [13] I. Auer, et al., “A New Instrumental Precipitation Dataset for the Greater Alpine Region for the Period 1800-2002,” International Journal of Climatology, Vol. 25, No. 2, 2005, pp. 139-166. doi:10.1002/joc.1135 [14] M. J. Menne and C. N. Williams Jr., “Detection of Un- documented Changepoints Using Multiple Test Statistics and Composite Reference Series,” Journal of Climate, Vol. 18, No. 20, 2005, pp. 4271-4286. doi:10.1175/JCLI3524.1 [15] M. J. Menne and C. N. Williams Jr., “Homogenization of Temperature Series via Pairwise Comparisons,” Journal of Climate, Vol. 22, 2009, pp. 1700-1717. [16] M. Brunet, M, O. Saladié, P. Jones, J. Sigró, E. Aguilar, A. Moberg, D. Lister, A. Walther, D. Lopez and C. Al- marza, “The Development of a New Dataset of Spanish Daily Adjusted Temperature Series (SDATS) (1850-2003),” International Journal of Climatology, Vol. 26, No. 13, 2006, pp. 1777-1802. doi:10.1002/joc.1338 [17] M. Brunet, O. Saladié, P. Jones, J. Sigró, E. Aguilar, A. Moberg, D. Lister, A. Walther and C. Almarza, “A Case-Study/Guidance on the Development of Long-Term Daily Adjusted Temperature Datasets,” WC-DMP-66/ WMO-TD-1425, 2008. [18] P. Domonkos, “Application of Objective Homogenization Methods: Inhomogeneities in Time Series of Temperature and Precipitation,” Időjárás, Vol. 110, 2006, pp. 63-87. [19] M. Brunet, J. Asin, J. Sigró, M. Bañon, F. García, E. Aguilar, J. E. Palenzuela, T. C. Peterson and P. Jones, “The Minimization of the Screen Bias from Ancient Western Mediterranean Air Temperature Records: An Exploratory Statistical Analysis,” International Journal of Climatology, Early View 2011, [20] T. C. Peterson and D. R. Easterling, “Creation of Homo- geneous Composite Climatological Reference Series,” International Journal of Climatology, Vol. 14, No. 6, 1994, pp. 671-679. doi:10.1002/joc.3370140606 [21] H. Alexandersson, and A. Moberg, “Homogenization of Swedish Temperature Data. Part I: Homogeneity Test for Linear Trends,” International Journal of Climatology, Vol. 17, No. 1, 1997, pp. 25-34. doi:10.1002/(SICI)1097-0088(199701)17:1<25::AID-JO C103>3.0.CO;2-J [22] M. Begert, T. Schlegel and W. Krichhofer, “Homogene- ous Temperature and Precipitation Series of Switzerland from 1864 to 2000,” International Journal of Climatol- ogy, Vol. 25, No. 1, 2005, pp. 65-80. doi:10.1002/joc.1118 [23] A. T. DeGaetano, “Attributes of Several Methods for Detecting Discontinuities in Mean Temperature Series,” Journal of Climate, Vol. 19, No. 5, 2006, pp. 838-853. doi:10.1175/JCLI3662.1 [24] D. M. Hawkins, “On the Choice of Segments in Piece- wise Approximation,” IMA Journal of Applied Mathe- matics, Vol. 9, No. 2, 1972, pp. 250-256. doi:10.1093/imamat/9.2.250 [25] H. Caussinus and F. Lyazrhi, “Choosing a Linear Model with a Random Number of Change-Points and Outliers,” Ann. Inst. Statist. Math, Vol. 49, No. 4, 1997, pp. 761-775. doi:10.1023/A:1003230713770 [26] COST HOME home-page. http://www.meteo.uni-bonn.de/venema/themes/homogeni sation/ [27] V. Venema, O. Mestre and the COST HOME Team, “Benchmark Database,” EGU General Assembly, Vienna, Austria, 3-7 May, 2010. [28] P. Domonkos, “Testing of Homogenisation Methods: Purposes, Tools and Problems of Implementation,” Pro- ceedings of the 5th Seminar and Quality Control in Cli- matological, Hungarian, 25-27 October 2006. Copyright © 2011 SciRes. IJG  P. DOMONKOS Copyright © 2011 SciRes. IJG 308 [29] Databases, (Ed. M. Lakatos, T. Szentimrey, Z. Bihari and S. Szalai), WCDMP-No. 71, 2008, pp. 126-145. [30] P. Domonkos, “Efficiency Evaluation for Detecting In- homogeneities by Objective Homogenisation Methods,” Theoretical and Applied Climatology, Early View 2011. doi:10.1007/s00704-011-0399-7  P. DOMONKOS309 Appendix: Explanation of Symbols and Acronyms The list below contains the explanation of symbols those are used throughout the paper. Note that one can find further explanations in the text about contemporary use of variables, as well as about some constants and pa- rameters whose role varies in the paper. Bold capital letter marks vector or matrix variable. A - anomaly ∆A - first difference (increment) of anomalies A* - adjusted anomaly B - normalised anomaly F - reference series g - index of candidate series G - penalty term h - serial number of month in a series hn - first month of a series hx - last month of a series H - timing of change-point in months H* - timing of selected change-point (in months) j - year k - serial number of change-point or that of section in fitted function K - total number of detected change-points for a time series K’ - number of detected change-points for a section of a time series l,L - length of series in a selected examination m - calendar month n - whole length of time series in years n’ - number of observed values in time series N - number of stations nm - length of relative time series in months p* - statistic of t-test q - serial number of relative time series Q - number of reference series for a specified candi- date series R - spatial correlation between first difference series R’ - spatial correlation s - station S - number of components of reference series T - relative time series T+ - unified relative time series T* - corrected relative time series TM - annual mean TD - summer-winter difference U - correction-term u’ - summarised impact / correction-term belongs to some selected IHs V - homogenised temperature w - sum of the squared correlations of reference components WR - error-term for raw time series WH - error-term for homogenised time series X - raw time series Y1 - first year of relative time series Y2 - last year of relative time series z, z* - indicator of significance of IHs α - shift in annual means at an IH β - shift in summer-winter differences at an IH σ - standard deviation ACMANT – Homogenisation method developed by the author: Adapted Caussinus-Mestre Algorithm for ho- mogenising Networks of Temperature series. ACMANTv0 – The version of ACMANT that took part in the blind test experiment of the COST HOME. ACMANTv1 – The version of ACMANT that is de- scribed in this paper. ANOVA – Equation-system based calculation method of correction-terms for homogenising time series. COST HOME / COST ES0601 – International scientific action on the development and testing of homogenisation methods. It is sponsored by the European Union. IH – Inhomogeneity: technical-born bias from the true climate in the series of observed data. MA – moving average PRODIGE – Homogenisation method that was devel- oped by Caussinus and Mestre (2004). RMSE – Root mean squared error. Copyright © 2011 SciRes. IJG
|