Received 11 February 2015; accepted 26 February 2015; published 3 March 2015

ABSTRACT

Mathematics is an interesting subject for some people, but for others are borings. The objective of this small paper is to stimulate Senior High school students’ scientific knowledge, when using the mathematical formula of circumference to determine longitude of universe and area in the Big Bang, as well as to introduce Cristosoles [1] numbers and antilogarithms. The paper shows a clear way to use simple mathematical formulas to determine the measure of the universe, besides relating the Cristosol numbers with the antilogarithms that can exist only in the antiuniverse; it is the first time that the antilogarithms have been defined.

Keywords:

Mathematics, Circumference, Area, Big Bang, Antilogarithm, Cristosoles

Subject Areas: Aerography

As it is known from Mathematics, the longitude of circumference is equal to:

, (1)

where r is the radio of circumference and π is the number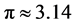, which is a constant. Then, this formula can be associated with the existence of universe assuming that the universe is enclosed in a circle. In fact it can be generalized to a sphere or an ellipse in revolution as we live in a three-dimensional world. But it will be worked by simplicity with a projection of universe in the plan and if someone wants to generalize three-dimensionally it can be carried out following a simple reasoning. Then, from (1) the following equation can be obtained:

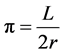, (2)

if it is supposed that the size of universe can be represented by its projection in a circle and that from the beginning there is a great explosion (Big Bang), this must have been done when the radio was equal to zero, which is all concentrated in a point of radio zero. Then, we ask ourselves the following question.

Which would be the size or longitude of universe at that time?

For this some maneuvers will be done.

Be r = 0 then of (2) it can be obtained:

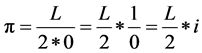(3)

as it is known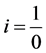, which is a Cristosol [1] , finding the initial longitude it can be obtained:

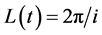, (4)

then this is the longitude of universe at the beginning, which is very small since i is immensely huge.

If it is known that the longitude of universe depends on time, it can be stated that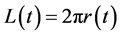, assuming the expansion linearity of (4) it can be obtained:

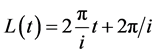(5)

Now measuring the time that delays the arrival of the light to the most distant observed star, it can be obtained then a current estimation of the longitude of universe, remembering that when,.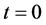

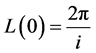Now two interesting cases will be seen.

・ 1st… When the elapsed time is very long which is equal to one Cristosol, that is.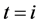

Substituting in (5),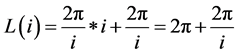

That is

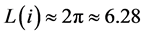(6)

years light, if the time is logically measured in years light, as it is known that the universe has a longitude greater than 6.28 years light, so the second case will be analyzed.

・ 2nd… If the time elapsed t = ni then substituting it can be obtained

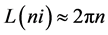(7)

Then, by practical measures it can be measured how many years light have elapsed since the explosion, that is, the value of L according to 5 can be obtained, which will be named L₅, and equal to L₇, finding n and despising

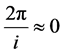
The number of Cristosoles elapsed can be obtained since the explosion of the material point with radio zero. Then,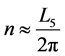. For more detailed reading of these numbers seen as group or rings, please see [2] .

Subsequently, some aspects of the area calculus of universe are developed during the Big Bang, as it is known that the longitude of universe at the beginning is of (4), but how much area has been taken? As we all know, the circle area is:

(8)

and as clearing r is left elevating to the square it can be obtained:

.

Then substituting in (8), we get that the area is equal to

.

Then substituting of (4) in A it can be obtained:

, (9)

because i² = −1, it can mean that the area is a negative number equal to −π. It is believed that it can mean an implosion or contraction of universe till the antiuniverse (Time < 0) (Figure 1).

It is necessary to clarify that, then. This is a property of the Cristosol’s numbers, because

the value i coincides with the i of the imaginaries numbers, and the Cristosols numbers are a mathematical group of the complex numbers Z (see [1] [2] ).

Another explicative way but of different result of the area in the Big Bang moment is clearing,

and if is left that is, clearing, and as according to (4) is left

then. That is the half area of the longitude in the Big Bang moment and at the same time the universe has a longitude twice the area, although this way is more comprehensive and explicative incurred in a

mathematical error when operating because and when, is left = that is.

The antiuniverse is a universe where the time can be negative (the negative area and the negative energy) (see application of the Cristosoles to the formula of energy [1] ). It is also made up of antimatter, antiprotons, antineutrons, antimagnetic, antineutrinos and antigravity and it cannot be missed certainly the negative logarithm o antilogarithms.

Interesting results are illustrated.

applying the logarithm in base e in both sides it is left:

(10)

Applying the logarithm in base i in both members of it is left

because (11)

Besides. Applying the logarithm in base e in each member it is left

(12)

because

Applying the logarithm in in base i it is obtained:

(13)

Generalizing it is obtained

(14)

or with the base i

(15)

We know the formula (Ver¹). When actually for Cristosoles it is fulfilled that, because and

Then applying logarithm of base 2 in both members it is obtained:

it is obtained: (16)

Changing the base of the logarithm in (12) to base 2, it is obtained

(17)

Then changing the base in (14) to log₂ of base 2 it is also obtained:

(18)

As it can be seen, the negative logarithm (antilogarithm) remains in function of known numbers.

Equations (16)-(18) seem to have no relationship with the main idea of this paper, Big Bang, but we put them here because it is a clear way to define the antilogarithm using the Cristosols numbers.

Cite this paper

Ricardo Osés Rodríguez,Rigoberto Fimia Duarte,Lisvette Cruz Camacho, (2015) Simple Model to Estimate Longitude and Area of Universe. Open Access Library Journal,02,1-4. doi: 10.4236/oalib.1101334

References