Received 20 January 2015; accepted 5 February 2015; published 9 February 2015

ABSTRACT

The magnetic, electrical and magnetotransport properties of spinel-type Mg(Fe_0.8Ga_0.2)₂O_4+δ ceramic ferrites have been investigated. The results of the investigations temperature and field dependences of magnetization and resistivity are presented and analyzed. The data of neutron scattering were found to be in good agreement with the Neel model of ferrimagnetism. This compound is magnetomonophase ferrimagnetic in the wide range of temperatures, and shows transition in paramagnet at high temperature (~490 K). Mg(Fe_0.8Ga_0.2)₂O_4+δ is characterized by maximal value of magnetization (28 emu/g) in the range of Mg(Fe_1−xGax)₂O_4+δ solid solutions. A negative magnetoresistance (MR) effect has been observed in Mg(Fe_0.8Ga_0.2)₂O_4+δ ferrite spinel. It has been determined that coefficient of the negative MR increased from 0.23% (at room temperature) to 7.28% (at 220 K). It can be explained with the help of the spin-dependent scattering on magnetic inhomogeneity of granular boundary.

Keywords:

Ferrimagnetic Spinel Oxide, Magnetic Structure, Vibration Magnetometry, Neutron Powder Diffraction, Magnetotransport

Subject Areas: Inorganic Chemistry, Inorganic Nonmetallic Materials

1. Introduction

One of the main problems of microelectronics is integration of magnetic materials in microcircuit. Microelectronics is based on semiconducting materials (Si, Ge, GaAs, GaN, etc.). To solve this problem is to search semiconductor materials with ferromagnetic properties. There are a number of requirements for these materials: 1) homogeneity (single-phase); 2) Curie temperature of materials must be higher than 150˚C (operating temperature range of microelectronic devices); 3) possibility of forming thin films on semiconducting substrates; 4) magnetoresistive effect. Material searching has some problems because most of homogeneous ferromagnetic (or ferrimagnetic) semiconductors (europium chalcogenides and oxides, cadmium-chromium spinels) are characterized of low Curie temperature [1] . Also these materials are mismatch with semiconducting materials. But it should be noted that there are many active studies in this area [2] [3] .

Ferrites constitute a technologically important class of metal oxides. Their high saturation moments and electrical resistance are exploited in high-frequency circuits, where they greatly reduce power losses from eddy currents. Other relevant uses of these materials are found in magnetic recording, microwave technology and heterogeneous catalysis. A key factor in all of these applications is the control of the relevant properties which can be exerted by means of intelligent design of chemical composition and crystal structure. Ferrites with general formula MFe₂O₄, where M is a divalent cation, have the spinel-type structure, space group. Cation distribution among (tetrahedral) A and (octahedral) B sites is of paramount relevance for many applications of spinel ferrites, since many of their properties (e.g. magnetic, semiconducting, catalytic) depend on such an ionic partition. It is in this context where ternary spinels (which may be regarded as solid solutions between two binary spinels) are particularly amenable. Introduction of the third cation allows control of the ionic partition, and hence of the relevant properties, by means of appropriate choice of substituent cation and chemical composition. However, the extent to which cation distribution can be modified in this way is difficult to foresee, since site occupancy in ternary spinels cannot be predicted (in general) by the concept of site preference energy as applied to binary spinel. Despite the considerable amount of experimental and theoretical work already done on the crystal chemistry of spinel solid solutions, a careful investigation of new systems can still be very valuable for a better understanding of these complex systems.

It’s observed that ferrite spinel properties are strongly depend on a number of requirements: method of producing, concentration substitution, size factor, anion nonstoichiometry, and defects. It is known that ferrite spinels as a rule are soft magnetic. They don’t need large magnetic fields for their magnetization. It was reported that diamagnetic substitution could induce changes in ferrospinel magnetic structure [4] [5] . In one case, frustrated magnetic structure consists of separate spontaneously magnetized areas formed due to long-range and short-range magnetic order. In such magnetic structures, substitution induces a decrease (in absolute value) of the average AB interaction with respect to AA and BB sites. As a consequence, the competition between negative intrasublattice and intersublattice interactions becomes strong, which leads to the formation of a cluster spin-glass state and frustrated magnetic structure [6] . For example in [7] , the authors noticed that composition CuGa_0.4Al_0.8Fe_0.8O₄ was characterized by isotropic magnetoresistive effect which increased with temperature decreasing. In the other case, substitution can induce of deviation in directions of magnetic moment vectors. The ferrites with canted B sites cations are called the YK-type ferrites. With specified concentration, the B site cations are no longer collinear. The spins of the B site cations are canted and make a certain angle [8] . In previously works [9] [10] , the authors noticed that more perspective compound in the solid solutions range Mg(Fe_1−xGa_x)₂O_4+δ (0 < x < 1) for investigation magnetoresistive effect is Mg(Fe_0.8Ga_0.2)₂O_4+δ. This compound is characterized by maximal values of magnetization (М_S = 28 emu/g), and conductivity (~10⁻⁸ Sm/m).

2. Experimental

Polycrystalline Mg(Fe_0.8Ga_0.2)₂O_4+δ sample was prepared by pyrohydrolitic method [11] at 1300 K. To carry out the pyrohydrolytic reactions, we prepared solution containing citric acid and a mixture of magnesium, gallium, and iron nitrates. The composition of the initial compound was determined on the basis of thermogravimetry (an ULVAC SINKU-RICO TGD 7000 thermal analyzer). The initial metal molar ratio in solutions was Mg:Ga:Fe = 1:0.4:1.6. The solution prepared was evaporated under continuous stirring in a porcelain bowl on a hot plate until a dense, viscous mass was formed. Then, pyrolysis began from the bottom of the bowl and rapidly (in 1 - 2 min) propagated over the entire volume. The reaction mixture was periodically stirred to complete the pyrolisis. The process was finished only when the reaction ceased (as monitored visually). The precursors obtained in this way were ground and annealed at 1250 - 1300 K.

The pyrohydrolytic reaction of combustion of the nitrates + citric acid initial mixture is as follows:

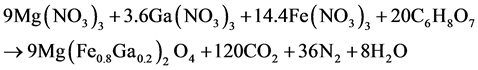
During the process of production time and temperature of synthesis were decreased in comparison with method of solid-state reactions. Crystal structure and phase analysis of polycrystalline Mg(Fe_0.8Ga_0.2)₂O_4+δ sample was carried out on a DRON-3M diffractometer using CuK_α radiation in the angular interval 25 deg < 2θ < 70 deg. Phases were identified with the use of the JCPDS PDF2 database. The Powder-2 program package was used for indexing X-ray diffraction patterns and calculating unit cell parameters. The magnetic structure of the Mg(Fe_0.8Ga_0.2)₂O_4+δ was determined by neutron powder diffraction (λ = 1.38 Å, scanning step Dθ ~ 0.1, angle range 10 deg ≤ 2θ ≤ 120 deg) on an reactor VVR-M in Gatchina. Magnetic properties (the temperature dependences of magnetization were measured in a field of 100 Oe in heating mode after zero field cooling (ZFC) and field cooling (FC), and Curie temperature were carried out a Helium Free Liquid system (by vibration magnetometry) in the 4.2 - 650 K temperature range temperature and field dependences of resistivity were investigated in the 200 - 300 K temperature range and magnetic field ranging 0 - 14 T. Energy of activation was calculated using the expression:

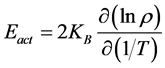
where ρ―resistivity; E_act―energy of activation; K_B―Boltzmann’s const, T―temperature.

Coefficient of negative magnetoresistive effect was calculated using the relation:

R_B―value of resistivity in magnetic field (14 T), R₀―value of resistivity without magnetic field.

3. Results and Discussions

3.1. Crystal Structure

The X-ray powder diffraction patterns of the Mg(Fe_0.8Ga_0.2)₂O_4+δ sample recorded at 25˚C and 300˚C [11] . The unit cell parameter а is 0.835(3) nm at 25˚C. At 300˚C, this value is 0.837(2) nm [11] . These data show that an increase in temperature considerably increases the unit cell parameter а of the spinel lattice. Apparently, temperature elevation leads to complex disordering processes in the crystal lattice of Mg(Fe_0.8Ga_0.2)₂O_4+δ [10] . Data of X-ray diffraction show that this compound is single-phase and thermostable in temperature range until 590 K, which makes this compound perspective for semiconductor electronics (the temperature range of stability for the materials used for semiconducting electronics is from −50˚C till 150˚C [11] . The analysis of the X-ray diffraction patterns indicates that the sample is described well (χ² = 2.4) by an orthorhombic spinel- like unit cell.

3.2. Magnetic Structure and Magnetic Properties

Temperatures dependences (ZFC and FC at 100 Oe) of magnetization are practically coinciding at interval 4.2 - 300 K (see Figure 1). This proves of sample magnetic homogeneity. Temperatures dependences data of Mg(Fe_0.8Ga_0.2)₂O_4+δ magnetization is evidence of thermal stability and absence of phase separation till 600 K.

From the temperature variation of the mass magnetization of the Mg(Fe_0.8Ga_0.2)₂O_4+δ ceramic (Figure 1) and its square (inset Figure 1), in the temperature range 300 - 650 K, the Curie temperature T_C of the ceramic was determined to be ~490 K (as curve bend of magnetization). The theoretical effective magnetic moment per Fe³⁺ ion (3d⁵ electronic configuration) is 5 μ_B/f.u., but the experimental data for the Mg(Fe_0.8Ga_0.2)₂O_4+δ ceramic give 1.4 μB/f.u. (summarized magnetic moment) for Fe³⁺ (28% of the theoretical value). The possible causes of the discrepancy are as follows: 1) coexistence of two magnetic spinel phases (or probably frustrated magnetic structure as in case of CuGa_0.4Al_0.8Fe_0.8O₄), 2) noncollinear magnetic vectors within a single magnetic phase (sperimagnetism) as in case of ferrite Yaffet-Kittel type, and 3) compensation of the magnetic moments of the A- and B-sublattices of the spinel due to gallium substitution for Fe³⁺ ions on the octahedral site. We concluded that reduced magnetic moment per Fe³⁺ ion attest to the third possibility. It must be noticed that frustrated

magnetic structure or noncollinear magnetic vectors in spinel structure can be cause of magnetoresistance in ferrite like spinel.

Neutron diffraction data were collected on a 48-counter powder neutron diffractometer [12] using monochromatic neutrons with the wavelength λ = 1.38 A at the VVR-M reactor in Gatchina (Konstantinov Petersburg Nuclear Physics Institute, RAS). The volume of a powder ceramic sample was ~0.3 cm³. Measurements were carried out in a vanadium container at 290 K. The resulting neutron diffraction pattern for Mg(Fe_0.8Ga_0.2)₂O_4+δ showed diffraction reflections for interplanar spacings in the dhkl range 0.8 - 7.0 A is shown in Figure 2. The unit cell parameters, oxygen atoms coordinates, magnetic moments per formula unit and the occupation numbers for Mg²⁺ and Fe³⁺ ions among tetrahedral and octahedral sites [13] were refined by the full-profile analysis method with the FULLPROF program [14] for space group and are given in insert of Figure 2. Oxygen parameter is u = 0.2556(2) as part of the lattice constant (distortion of the oxygen arrangement from cubic close- paking).

The distribution of chemical elements at A- and B-sites in this sample is [Mg_0.20(3)Fe_0.72(3)] (Fe_0.44(3)Mg_0.40(3)Ga_0.2)₂O₄. The orientation and magnitude of magnetic moments were determined simultaneously with the FULLPROF program. Effective magnetic moment of Fe³⁺ in tetrahedral coordination is 1.2 μ_B and effective magnetic moment of Fe³⁺ in octahedral coordination is 1.85 μ_B. The average ferrimagnetic moment of Fe³⁺ (summarized magnetic moment of f.u.) is 1.53 μ_B/f.u. that close to the value calculated according to vibration magnetometry data.

On the ground of neutron powder diffraction data (calculated with Fullprof) we concluded that diamagnetic substitution in Mg(Fe_0.8Ga_0.2)₂O_4+δ doesn’t induce formation of frustrated magnetic structure as in case of CuGa_0.4Al_0.8Fe_0.8O₄ and doesn’t induce deviation from collinearity of magnetic vector’s directions in Mg(Fe_0.8Ga_0.2)₂O_4+δ as in case of ferrite Yaffet-Kittel type.

3.3. Electrical and Magnetotransport Properties

Due to the high resistivity of the sample (at 300 K is approximately 5.9 MΩ*cm) and the limitation of current source of the measuring system, resistivity was measured between 300 and 220 K as shown in Figure 3. It is found that the resistivity increases (approximately on the 3 order of magnitude in temperature interval 300 - 220

K) as the temperature decreases, and calculated Е_act that corresponds energy of impurity activation. Behavior of resistivity Mg(Fe_0.8Ga_0.2)₂O_4+δ is characterized by semiconducting type of conductivity. As shown in Figure 3 ρ at 300 K is equal 5.9 MΩ*sm, and ρ at 220 K ~ 2.1 GΩ*sm.

The strong increase in resistivity with decreasing T can be understood in terms of a thermally activated hopping type transport mechanism of the itinerant electrons on the B-sublattice. It was determined that in this compound predominate impurity type of conductivity. From the hopping amplitude t ~ 0.1 eV an electron conduction bandwidth ~1 eV is expected. However, experimental data cannot be explained within a simple band theory. They can be better ascribed to some thermally activated motion of charge carriers. It have been shown that below 250 K energy of impurity activation is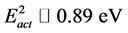, and above 250 K till 300 K energy of impurity activation is. As has been shown by neutron diffraction data there isn’t some spin canting between A- and B-sublattices. This hasn’t been to taken into account by an appropriate spin correlation factor leading to a spin-dependent part of the activation energy.

Behavior of Mg(Fe_0.8Ga_0.2)₂O_4+δ magnetoresistance (MR) in the presence of 14 T field and at different temperatures was investigated (see Figure 4). In our case Mg(Fe_0.8Ga_0.2)₂O_4+δ we have intergranular contribution in MR. This contribution is depends on spin-polarized carrier scattering on magnetic heterogeneity of granular

boundary. This is due to multidirectional of crystallines magnetization vectors. For this sample 7.38% negative MR is observed at 220 K in the presence of 14 T field. Then MR coefficient is monotonic decreases with temperature increasing. At room temperature MR is 0.23%. It can be explained by decreasing of spin polarization coefficient of magnetic heterogeneity local spins in granular boundary.

Theoretically in case of thermally activated hopping-type conductivity we may estimate that coefficient of spin polarization deeply decreases with increasing semiconductor’s band gap. Controlling of electron spin direction in this compound is an intricate problem. In case of Mg(Fe_0.8Ga_0.2)₂O_4+δ magnetic semiconductor low coefficient of magnetoresistance may be associated with low degree of electron spin polarization.

4. Conclusions

This compound Mg(Fe_0.8Ga_0.2)₂O_4+δ which was prepared by pyrohydrolitic method was magnetomonophase ferrite spinel with T_C ~ 490 K. In the process of production, time and temperature of synthesis were decreased in comparison with method of solid-state reactions. It has been determined that diamagnetic substitution Fe³⁺ ions by Ga³⁺ ions in Mg(Fe_0.8Ga_0.2)₂O_4+δ doesn’t induce formation of frustrated magnetic structure and doesn’t induce deviation from collinearity of magnetic vector’s directions. The distribution of chemical elements is [Mg_0.20(3)Fe_0.72(3)](Fe_0.44(3)Mg_0.40(3)Ga_0.2)₂O₄. Effective magnetic moment of Fe³⁺ in tetrahedral coordination is 1.2 μ_B and effective magnetic moment of Fe³⁺ in octahedral coordination is 1.85 μ_B. The average ferrimagnetic moment of Fe³⁺ calculated from neutron diffraction data is 1.53 μ_B/f.u. which is close to the value calculated according to vibration magnetometry data (1.4 μ_B/f.u.). Coefficients of the negative MR are increasing from 0.23% (at room temperature) to 7.28% (at 220 K). The nature of negative MR in Mg(Fe_0.8Ga_0.2)₂O_4+δ is caused by increasing spin polarization of local spins in the magnetic heterogeneity of granular boundary.

Highest values of magnetization and electroconductivity in the range of Mg(Fe_1−xGa_x)₂O_4+δ solid solutions with the aggregate MR-phenomenon make this compound promising for practical application. By integrating such thin Mg(Fe_0.8Ga_0.2)₂O_4+δ layers into spin-dependent tunnelling heterostructures, it can be demonstrated that this material can be useful for magnetic tunnel junctions or as a spin-filtering insulating barrier in the little explored type of tunnel junction called spin-filter.

Cite this paper

A. V. Trukhanov,S. V. Trukhanov,O. P. Smirnov,A. A. Kulikov,H. Szymczak, (2015) Magnetic, Electrical and Magnetotransport Properties of Mg(Fe_0.8Ga_0.2)₂O_{4 δ} Obtained by Pyrohtdrolitic Method. Open Access Library Journal,02,1-7. doi: 10.4236/oalib.1100842

References

NOTES

^*Corresponding author.