Received 7 January 2015; accepted 23 January 2015; published 27 January 2015

ABSTRACT

The possibility of the description of the available experimental data for cross sections of the neutron capture reaction on ¹⁰B at thermal and astrophysical energies, taking into account the resonance at 475 keV, was considered within the framework of the modified potential cluster model with forbidden states and accounting for the resonance behavior of the scattering phase shifts.

Keywords:

Nuclear Astrophysics, Primordial Nucleosynthesis, Light Atomic Nuclei, Low and Astrophysical Energies, Radiative Capture, Thermonuclear Processes

Subject Areas: Nuclear Physics

1. Introduction

Light radioactive nuclei play an important role in many astrophysical occurrences. Such parameter as a total cross section of the capture reactions as a function of energy is very important for investigation of many astrophysical problems such as primordial nucleosynthesis of the universe, main trends of stellar evolution, novae and super-novae explosions, X-ray bursts, etc. The continued interest in the study of processes of radiative neutron capture on light nuclei at thermal and astrophysical energies is caused by several reasons. Firstly, this pro- cess plays a significant part in the study of many fundamental properties of nuclear reactions; and secondly, the data on the capture cross sections are widely used in a various applications of nuclear physics and nuclear astrophysics, for example, in the process of studying of the primordial nucleosynthesis reactions.

One extremely successful line of development of nuclear physics in the last 50 years has been the microscopic model known as the Resonating Group Method (RGM, see, for example, [1] - [5] ), and the associated Generator Coordinate Method (GCM, see, particularly, [5] [6] ) or algebraic version of RGM [7] .

However, the possibilities offered by a simple two-body potential cluster model (PCM) have not been studied fully up to now, particularly if it uses the concept of forbidden states (FSs) [8] , and considers directly the resonance behavior of the elastic scattering phase shifts of interacting particles at low energies [9] [10] . Such a model can be called a modified PCM (MPCM). The rather difficult RGM calculations are not the only way in which to explain the available experimental facts. The simpler MPCM with FSs can be used by taking into account the classification of orbital states according to the Young tableaux and the resonance behavior of the elastic scattering phase shifts. In many cases, such an approach, as has been shown previously [9] [10] , allows one to obtain adequate results in the description of many experimental data for the total cross sections of the thermonuclear capture process.

Particularly, in works of [11] [12] , we have shown the possibility of description the Coulomb form-factors of lithium nuclei on the basis of potential cluster model [9] [13] [14] . As we have just said, this model takes into account forbidden states [13] - [18] in the intercluster potentials, which are determined on the basis of the classification according to Young tableaux and were used by us in [19] [20] . Furthermore, in [21] [22] , we show the possibility of the correct reproduction practically all characteristics of ⁶Li, including its quadrupole moment in the potential cluster model with tensor forces [15] . And finally, in [9] [13] [14] [23] - [41] , the possibility of description of the astrophysical S-factors or the total cross sections of the radiative capture for n²H, p²H, p³H, n⁶Li, p⁶Li, n⁷Li, p⁷Li, p⁹Be, n⁹Be, p¹⁰B, p¹¹B, n¹¹B, n¹²C, p¹²C, n¹³C, p¹³C, n¹⁴C, p¹⁴C, n¹⁴N, n¹⁵N, p¹⁵N, n¹⁶O and ²H⁴He, ³He⁴He, ³H⁴He, ⁴He¹²C systems at thermal and astrophysical energies is considered. These calculations of the listed above capture processes are carried out on the basis of the modified variant of PCM, described in [9] [10] [37] - [39] .

Therefore, in continuing to study the processes of radiative capture [9] [10] , we will consider the 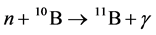reaction within the framework of the MPCM at low and thermal energies. The resonance behavior of the elastic scattering phase shifts of the interacting particles at low energies will be taken into account. In addition, the classification of the orbital states of the clusters according to the Young tableaux allows one to clarify the number of FSs and allowed states (ASs), i.e., the number of nodes of the wave function of the relative motion of the cluster. The potentials of the n¹⁰B interaction for scattering processes will be constructed based on the reproduction of the spectra of resonance states for the final nucleus in the n¹⁰B channel. The n¹⁰B potentials are constructed based on the description both of the binding energies of these particles in the final nucleus and of certain basic characteristics of these states; for example, the charge radius and the asymptotic constant (AC) for the bound state (BS) or the ground state (GS) of ¹¹B, were formed as a result of the capture reaction in the cluster channel, which coincides with the initial particles [10] .

The study of the reaction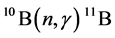, from the astrophysical point of view, is interesting because the resultant ¹¹B is a part of the reaction chains in the so-called inhomogeneous Big Bang models [42] - [46] . Therefore, it is interesting to consider the additional chain of these reactions starting from the boron isotope ¹⁰B:

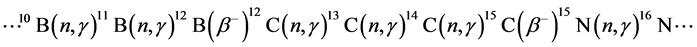(1)

Evidently, the considered reaction can play a certain role in some models of the universe [42] - [46] , when the number of forming nuclei, perhaps, is dependent on the presence of dark energy and its concentration [47] , on the rate of growth of baryonic matter perturbations [48] , or on the rotation of the early universe [49] . However, perturbations in the primordial plasma not only stimulate the process of nucleosynthesis [50] , but also kill it, for example, through the growth of the perturbations of nonbaryonic matter of the universe [51] or because of the oscillations of cosmic strings [52] .

However, it seems to us that the study of this reaction is also interesting, even though that it has been impossible for us to find any similar theoretical calculations for the reaction 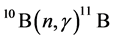in thermal and astrophysical energy range. In addition, ¹⁰B is a very good absorber of neutrons that it is used in control rods in nuclear reactors. This property also makes it useful for construction of neutron detectors. Boron is used to make windows that are transparent to infrared radiation, for high-temperature semiconductors, and for electric generators of a thermoelectric type [53] .

2. Structure of Cluster States

We regard the results of the classification of ¹¹B by orbital symmetry in the n¹⁰B channel as qualitative, because there are no complete tables of Young tableaux productions for systems with more than eight nucleons [54] , which have been used in earlier similar calculations [9] [10] . At the same time, simply based on such a classification, we succeeded in describing the available experimental data on the radiative capture of neutrons and charged particles for a wide range of reactions of [9] [10] [35] [37] [39] . This is why the classification procedure by orbital symmetry given above was used here for the determination of the number of FSs and ASs in partial intercluster potentials and, consequently, to the specified number of nodes of the wave function of the relative motion of the cluster for the case of neutrons and ¹⁰B.

Furthermore, we will suppose that it is possible to assume the orbital Young tableau in the form 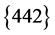for ¹⁰B; therefore, for the n¹⁰B system, we have 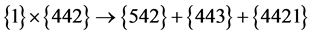[54] . The first of the obtained tableaux is compatible with orbital moments, 2, 3, and 4, and is forbidden because it contains five nucleons in the s-shell. The second tableau is allowed and is compatible with orbital moments, 2, 3, and 4, and the third is also allowed and is compatible with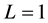, 2, and 3 [55] . As mentioned before, the absence of tables of Young tableaux productions for when the number of particles is 10 and 11 prevents the exact classification of the cluster states in the considered system of particles. However, qualitative estimations of the possible Young tableaux for orbital states allow us to detect the existence of the FSs in the S and D waves and the absence of FSs for the P states. The same structure of FSs and ASs in the different partial waves allows us to construct the potentials of intercluster interactions required for the calculations of the total cross sections for the considered radiative capture reaction. Thus, by limiting our consideration to only the lowest partial waves with orbital moment, and 1, it could be said that for the n¹⁰B system (for ¹⁰B it is known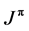, , 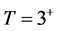0) [56] , the only allowed state exists in the P wave potentials and the FS is in the S waves. The state in the ⁶Р_3/2 wave (representation in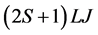) corresponds to the GS of ¹¹B with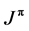, , 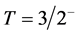1/2 and is at the binding energy of the n¹⁰B system of −11.4541(2) MeV [57] . Let us note that some n¹⁰B scattering states and BSs can be mixed by isospin with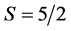 and .

The spectrum of ¹¹B for excited states (ESs), bound in the n¹⁰B channel, shows that at the energy of 2.1247 MeV above the GS or −9.3329 MeV [57] relative to the threshold of the n¹⁰B channel, the first ES can be found, bound in this channel with the moment, which can be compared with the ⁶F_1/2 wave with an FS. However, we will not consider it, because of the large value of the angular momentum barrier. The second ES at the energy 4.4449 MeV [57] above the GS or −7.0092 MeV relative to the threshold of the n¹⁰B channel has the moment, and it can be compared with the mixture of the ⁶P_5/2 and ⁸P_5/2 waves without FSs. Furthermore, the unified potential of such a mixed P_5/2 state will be constructed, because the model used does not allow one to divide states with different spin clearly. The wave function obtained with this potential at the calculation of the Schrödinger equation and, in principle, consisting of two components for different spin channels, does not divide into these components in the explicit form, i.e., we are using the total form of the WF in all calculations. The third ES at the energy of 5.0203 MeV [57] relative to the GS or −6.4338 MeV relative to the channel threshold has the moment, and it can be matched to the ⁶P_3/2 wave without an FS. The fourth ES at the energy of 6.7429 MeV [57] relative to the GS or −4.7112 MeV relative to the channel threshold has the moment, and it can be matched to the mixture of the ⁶P_7/2 and ⁸P_7/2 waves without an FS. In addition, it is possible to consider the ninth ES at the energy of 8.9202 MeV with the moment 5/2⁻, i.e., at the energy of −2.5339 MeV relative to the n¹⁰B threshold, which can be matched to the mixture of the ⁶P_5/2 and ⁸P_5/2 states without FSs.

Consider now the resonance states in the n¹⁰B system, i.e., states at positive energies. The first resonance state of ¹¹B in the n¹⁰B channel, located at the energy 0.17 MeV, has the neutron width of 4 keV and the moment [57] . It is possible to compare this state with the ⁶S_5/2 scattering wave with an FS. We have not succeeded in the construction of the potential with such small width; therefore, we will consider this scattering wave as non-resonant, which leads to zero scattering phase shifts. The second resonance state has the energy of 0.37 MeV―its neutron width equals 0.77 MeV and the moment [57] ; therefore, it is possible to compare this with the ⁸S_7/2 scattering wave with an FS. Because of the large width of resonance (two times greater than its energy), we will use non-resonant values of the parameters for the potential to coincide with the previous ⁶S_5/2 potential. The third resonance state has the energy of 0.53 MeV in the laboratory system (l.s.)―its neutron width equals 0.031 MeV in the center-of-mass system (c.m.) and the moment [57] . Therefore, it can be compared with the mixed ⁶P_5/2 + ⁸P_5/2 scattering waves without FSs. These characteristics of the resonance are given in Table 11.11 of [57] , and in the note to this table are given the energy and the width values equal to 0.495(5) MeV and 140(15) keV, respectively, with reference to [58] . At the same time, the value of 0.475(17) MeV (l.s.) with the total width 200(20) keV (c.m.) is given in Table 11.3 of [57] for this resonance. Furthermore, under the construction of this potential, we will proceed from two variants of data, notably, the first and the last given above with the width of 31 keV (c.m.), but at the energy of the resonance of 475 keV (l.s.), which follows from the level spectrum [57] .

The next resonance is at the energy above 1 MeV and we will not consider it (see Table 11.11, [57] ). There are no resonance levels lower than 1 MeV in the spectrum of ¹¹B that can be matched to the ⁶P_3/2 and ⁶⁺⁸P_7/2 states [57] . Therefore, their phase shifts are taken as equal to zero, and as far as there are no FSs in the P waves, by way of the first variant, such potentials can be simply equalized to zero [9] [10] . We ought to note here that there are more up-to-date values for all these states [59] ―the results from this review do not differ for the ESs (see Table 11.18, [59] ), but do have slightly different values for resonance states. Particularly, the excited energy of 11.893(13) MeV with the adjusted total width of 194(6) keV, which gives 483 keV (l.s.) for the resonance energy, is given for the state, which can be matched to the ⁶⁺⁸P_5/2 scattering waves without FSs. The width equal to 1.34 MeV, which is given for the state with, compares with the ⁸S_7/2 scattering wave with an FS―it is twice that given in [57] .

Continuing to the analysis of possible electromagnetic E1 and M1 transitions, let us note that we will consider only transitions to the GS and to four (2^nd, 3^rd, 4^th, and 9^th) ESs from the S and P scattering waves. One can see Table 1.

3. Methods of Calculation

The total radiative capture cross sections for the ЕJ and МJ transitions in the case of the PCM are given, for example, in [61] or [9] [10] [12] [62] and they have the following form:

(2)

where―total radiative capture cross section;―reduced mass of initial channel particles;―wave number in initial channel;,―spins of particles in initial channel;,―wave number and angular momentum of -quantum in final channel;―is the or transitions of the multipole ordered from the initial to the final nucleus state.

The value for electric orbital transitions has the form of [9] [10] [61]

(3)

Here, , , , , , and―total spins, orbital and total angular momenta in initial and final channels;, , ,―masses and charges of the particles in initial channel;―integral over wave functions of initial and final states, as functions of cluster relative motion of n and ¹⁰B particles with intercluster distance.

For consideration of the magnetic transition, caused by the spin part of magnetic operator [63] , it is possible to obtain an expression of [9] [10] using the following [64] :

(4)

Here, is the mass of the nucleus, and and are the magnetic moments of the clusters, the values

of which are taken from [65] [66] .

The construction methods used here for intercluster partial potentials at the given orbital moment, are expanded in [9] [10] [36] and here we will not discuss them further. The next values of particle masses are used in the given calculations: amu (see [65] ) and amu (see [67] ), and constant is equal to 41.4686 MeV fm².

4. Interaction Potentials

For all partial waves of the n¹⁰B interaction potentials, i.e., for each partial wave with the given, we used the Gaussian potential of the form:

. (5)

Here, as mentioned before, we will not consider the influence of the first resonance at 0.17 MeV in the ⁶S_5/2 wave; therefore, we will use the potential with FSs leading to the zero scattering phase

. (6)

The ⁶S_5/2 scattering phase shift of this potential at energy up to 1.0 MeV is less than 0.5˚. The same parameters we be used for the ⁸S_7/2 scattering wave, also ignoring the resonance.

The following parameters were obtained for the third resonance state at 0.475(17) MeV:

. (7)

Such potential leads to resonance, i.e., the scattering phase shift equals 90.0˚, at 475(1) keV (l.s.) with a width of 193(1) keV (c.m.), which is in good agreement with the data of [57] [59] .

For the potential of the pure-by-spin GS of ¹¹B in the n¹⁰B channel, where the 6P_3/2 wave is used, the following parameters were obtained:

. (8)

We have obtained the value of the dimensionless AC = 1.53(1) in the range of 3 - 10 fm, the charged radius of 2.44 fm, and the mass radius of 2.39 fm at the binding energy of −11.454100 MeV with the accuracy of the finite-difference method, used for the calculation of the binding energy at [16] . The AC error is connected with its averaging over the above-mentioned range of distances. The phase shift for such potential decreases smoothly until a value of 179˚ when the changes from zero to 1.0 MeV. The generalized Levinson theorem [8] is used for the determination of the value of scattering phase shift at zero energy.

The AC value equal to 1.72 fm^−1/2 was obtained in Ref. [68] for the GS of ¹¹B in the cluster channel n¹⁰B, where the coefficient of neutron identity was assigned (see expression 83b in [69] ). In this work, a slightly different definition of AC was used, notably (with the Coulomb parameter equals zero, in this case), which is different from our previous works [9] [10] to the value that equals 1.19 fm^−1/2 for the GS; therefore, the AC value equals 1.44 in the dimensionless form. The improved value of 1.82(15) fm^−1/2 is given in the latest results for this AC (see [70] ), and after re-computation, it gives 1.52(12) in the dimensionless form and agrees absolutely with the value for the GS potential (8) obtained here.

The parameters of the GS potential and any BSs in the considered channel at the given number of the bound, allowed or forbidden states in the partial wave, are fixed quite unambiguously by the binding energy, the charge radius, and the asymptotic constant. The accuracy of the determination of the BS potential parameters is connected with the accuracy of the AC, which is usually equal to 10% to 20%. There are no another ambiguities in this potential, because the classification of the states according to the Young schemes allows us unambiguously to fix the number of BSs in this partial wave, which defines its depth completely, and the width of the potential depends wholly on the values of the charge radius and the AC.

The next parameters were obtained for the parameters of the potential without FSs for the second ES of ¹¹B in the n¹⁰B channel with:

. (9)

This potential leads to the binding energy of −7.0092 MeV at, which is completely coincident with the experimental value from [57] [59] for the charge radius of 2.44 fm, and the AC of 1.15(1) at the range of 3 - 13 fm.

The next parameters were obtained for the potential without FSs for the third ES ⁶Р_3/2 pure-by-spin with:

. (10)

These parameters lead to the binding energy of −6.4338 MeV at coinciding with the experimental value of [57] [59] ; the AC equals 1.10(1) at the range of 3 - 13 fm, and the charge and mass radii are equal to 2.44 fm and 2.41 fm, respectively. The scattering phase shift for this potential decreases until 178˚ at the energy of 1.0 MeV.

The next parameters were obtained for the potential without FSs for the fourth ES of ¹¹B in the n¹⁰B channel with:

. (11)

The binding energy of −4.7112 MeV at, which absolutely coincides with the experimental value of [57] [59] for the charge radius of 2.44 fm, and dimensionless AC equal to 0.94(1) at the range of 3 - 15 fm, was obtained with this potential. The scattering phase shift for this potential decreases smoothly until 178˚ at the energy of 1.0 MeV.

These parameters were obtained for the potential without FSs for the ninth ES of ¹¹B in the n¹⁰B channel with:

. (12)

This potential leads to the binding energy of −2.5339 MeV at, which completely coincides with the experimental value of [57] [59] for the charge radius of 2.44 fm, and dimensionless AC equal to 0.70(1) at the range of 3 - 24 fm. The scattering phase shift for this potential decreases smoothly until 178˚ at the energy of 1.0 MeV.

5. The Total Cross Section of the Radiative Neutron Capture on ¹⁰B

The next experimental data were used for the comparison of the calculation results given in Figure 1 and Figure 2. The black points (●) show the total summed capture cross section from [60] at 23, 40, and 61 keV. The triangle (▲) represents the cross section of 500(200) μb from [71] at the energy of 25 MeV, and the open reverse triangle (Ñ) shows the new results for the cross section of 305(16) μb at 25 MeV from [72] , given in the review [59] . It should be noted that other data for 390(11) μb, obtained in [73] and also shown in Figure 1 and Figure 2 by the open reverse triangle (Ñ), were published later; reference to these results is also given in review [59] . The experimental measurements of [60] for the transitions to different ESs of ¹¹B are shown in Figure 1 and Figure 2: open circles (o) represent the total capture cross section to the GS ⁶Р_3/2, open squares (□) represent the total capture cross section to the second ES ⁶⁺⁸Р_5/2, black squares (■) represent the total capture cross section to the fourth ES ⁶⁺⁸Р_7/2, and open triangles (D) represent the total capture cross section to the ninth ES ⁶⁺⁸Р_5/2. Furthermore, in Figure 3, only part of these experimental results is given.

The E1 transition from the S scattering wave with potential (6) to the GS with potential (8) was considered initially in our calculations, and the obtained capture cross section is shown in Figure 1, represented by the short dashed line. The general dashed line shows the capture cross section to the second ES for potential (9), identified in Section 2 as No. 2. The dotted line shown at the bottom of Figure 1 denotes the cross section of the transition to the third ES (10). The dot-dashed line shows the cross section of

the transition to the fourth ES (11), identified in Section 2 as No. 4. The dot-dot-dashed line, which is almost superimposed with the dotted line, shows the transition from the S scattering waves to the ninth ES with potential (12). The solid line gives the total summed cross section of all the above considered transitions, which largely describes the experimental data for the total summed cross sections from [60] [71] at the energy range from 25 MeV to 61 keV correctly.

Let us note that in the measurements of [60] the transition to the third ES is not taken into account, and as seen in Figure 1, this leads to nearly the same cross section of the transition to the third ES and the ninth ES- dotted and dot-dot-dashed lines. Therefore, probably, it is necessary to add the cross section of the transition to the ninth ES to the total cross sections [60] to obtain summed cross sections that are more correct, and this will be equivalent to taking into account the transition to the third ES. Such cross sections are shown in Figures 1-3 by the open rhombus―this account influences weakly the total cross sections, which also agree with the results of our calculations.

As can be seen from the obtained results, the calculated line for the transition to the fourth ES is in a good agreement with the given black squares (experimental data) [60] . The good agreement of the calculation, shown by the dot-dot-dashed line, can also be observed for the transition to the ninth ES, the experiment for which is shown by the open triangles [60] . The measurements for the transition to the second ES, shown in Figure 1 by the open squares [60] , lie appreciably higher than the corresponding calculated line, shown by the dashed line. The measurements of the cross section for the transition to the GS, shown by the open circles [60] , lie much lower than the calculated line, shown by the short dashed line. Thereby, only two calculations conform to the experimental results for the transitions to the fourth and ninth ESs [60] , although the total summed cross sections, shown by the black points or rhombus, are described completely by the calculated line―the solid line in Figure 1.

Because, we do not know the AC value for the second ES, it is always possible to construct the potential correctly describing the capture cross sections to this state, shown in Figure 1 and Figure 2 by the open squares [60] . For example, it is possible to use the potential with the parameters:

, (13)

which leads to the binding energy of −7.0092 MeV, the charged radius of 2.44 fm, and the value of the AC equal to 1.45(1) at the range of 4 - 13 fm. The calculation results of the capture cross sections to this state from the S scattering waves are shown in Figure 2 by the dashed line, which is in a quite agreement with the experimental data [60] shown by the open squares.

At the same time, the other variant of the GS potential that describes the total capture cross sections to the GS correctly, shown in Figure 1 and Figure 2 by the open circles, will not agree with the known AC or that given above for the GS. For example, the parameters

(14)

Allow one to describe reasonably the available experimental cross section measurements of the transition [60] , as is shown in Figure 2 by the short dashed line. However, although this potential leads to the correct binding energy of −11.454100 MeV and describes reasonably the charged radius of 2.43 fm, the value of the AC is equal to 0.71(1) at the range of 2 - 8 fm, which is half that of the results from other experimental data [68] [70] . This result can be explained by the imperfection of the MPCM used here; however, on such occasions, the MPCM led to the correct description of the cross sections both to the transitions to the GS and to the total summed cross section of the capture processes [9] [10] [36] [39] . Therefore, it could be supposed that the experimental measurements for transitions to different ESs of ¹¹B at the radiative neutron capture on ¹⁰B should be improved in the future; it will also be interesting to obtain new data in the range of possible resonances from 100 to 600 keV.

Reverting to the calculation results given in Figure 1, we note that at the energies from 10 MeV to 10 keV, the calculated cross section is almost a straight line, and it can be approximated by a simple function of the form:

. (15)

The value of the given constant A = 2123.4694 μb∙keV^1/2 was determined from a single point of the cross-sec- tions (solid line in Figure 1) at a minimal energy of 10 MeV. The absolute value of the relative deviation of the calculated the oretical cross sections, and the approximation of this cross section by the expression given above in the energy range until10 keV, is at the level of 0.2%. It is supposed that this form of total cross section dependence on energy will be conserved at lower energies. In this case, the estimation of the cross section value, for example, at the energy of 1 μ keV, gives the value of 67.2 b. The coefficient for the solid line in Figure 2 in the expression given above (15) for the approximated calculation results for cross sections, is equal to 2150.3488 μb∙keV^1/2.

Furthermore, the considered M1 transitions to the GS and to the different ESs are shown in Figure 3, together with the summed cross section for the E1 processes, which is shown by the dashed line (it is represented by the solid line in Figure 1). The dotted line at the top of the figure shows the cross section of the M1 transition to the GS with potential (8) from the resonant ⁶Р_5/2 scattering wave for potential (7), identified in Section 2 as No. 6. The dot-dashed line it is the transition from the Р_5/2 scattering wave (7) to the second ES with potential (9), identified in Section 2 as No. 7. The dot-dot-dashed line shows the cross section of the M1 transition to the third ES with potential (10) in Figure 3. Another possible M1 transition to the fourth ES (11), identified in Section 2 as No. 9, has the form of the cross section shown in Figure 3 by the short dashes. In addition, the M1 transition to the ninth ES (12) is possible; it is identified in Section 2 as No. 10, and shown in Figure 3 by the dot-dashed line with closely placed dashes (the third line at the bottom), which lies slightly higher than the short dashed line. In addition, the M1 transition to the GS from the non-resonant ⁶Р_3/2 scattering wave was considered with the potential of zero depth―the second transition under No. 6 in Section 2. The result is shown by the dotted line with closely placed dots in the bottom of Figure 3. Its value at the maximum is about 1.5 μb and it has practically no influence on the calculated cross sections in the range of the resonance at 475 keV, almost reaching to 4.5 mb. Experimental data: points (●)―the total summed cross section of the neutron capture on ¹⁰B from [60] , open rhombus (◊)―the summed total capture cross section from [60] taking into account the transition to the third ES.

The sum of all the E1 and M1 transitions described above is shown in Figure 3 by the solid line, which gives a suitable description of the given experimental data. The small overshoots of the calculated cross sections over the experimental one at 40 and 61 keV can be used to argue that the used potential (7) leads to the overestimated value of the resonance width in the Р_5/2 scattering wave of 193 keV.

6. Conclusions

As can be seen from the listed results, the obvious assumptions about the methods of construction of the n¹⁰B interaction potentials, if they have FSs, allow one to obtain acceptable results on the description of the available experimental data for the total cross section of the neutron capture on ¹⁰B of [60] [71] [73] at the energy range from 25 MeV to 61 keV. The possibility to describe all considered experimental data both by capture cross section and according to the GS characteristics, allows us to fix parameters of the GS potential closely enough in the form of (8). The summed cross sections at the resonance energy of 0.475 MeV, are equal to 4.5 μb at the width of the resonance of 193 keV and 13.7 μb at the width of 32 keV.

Thereby, the MPCM again confirms, as already done in 27 reactions from [9] [10] [23] - [26] [30] [31] [35] - [39] [74] - [80] , its ability to describe correctly the cross sections of the processes such as the radiative capture of neutral and charged particles on light nuclei at thermal and astrophysical energies. As this occurs, such results are obtained using the potentials matched with the resonance scattering phases, or with the level spectra of the final nucleus and the BS characteristics of the considered nuclei, and some basic principles of the construction of such potentials were checked partially in the three-body calculations of [81] .

Acknowledgements

In conclusion, the authors express their deep gratitude to Prof. Yarmukhamedov R. (INP, Tashkent, Uzbekistan) for provision of the information on the AC in the n¹⁰B channel, and also to Prof. Strakovsky I.I. (GWU, Washington, USA) and to Prof. Blokhintsev L.D. (MSU, Moscow, Russia) for discussions of certain questions touching in the paper.

Cite this paper

S. B. Dubovichenko,A. V. Dzhazairov-Kakhramanov, (2015) Astrophysical Radiative Neutron Capture on ¹⁰B Taking into Account Resonance at 475 keV. Open Access Library Journal,02,1-13. doi: 10.4236/oalib.1101263

References

NOTES

^*Corresponding author.