Open Access Library Journal
Vol.02 No.01(2015), Article ID:68009,7 pages
10.4236/oalib.1101184
Cross Correlation Analysis of Mozambique’s 7.0 M Earthquake using the empirical Mode decomposition
Enoch Oluwaseun Elemo
Centre for Atmospheric Research, Anyigba, Nigeria
Email: enochelemo@yahoo.com
Copyright © 2015 by author and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 January 2015; accepted 23 January 2015; published 27 January 2015
ABSTRACT
Precise determinations of ionospheric anomaly variations associated with earthquakes require the elimination of other sources of ionospheric variabilities like ionospheric storms, geomagnetic perturbations or geophysical noise. However, revealing the seismo-ionospheric anomalies when the ionosphere is known to be a complex and nonlinear system is of utmost importance. To overcome this constraint, Hilbert-Huang transform (HHT), which is a far better technique for both nonlinear and non-stationary system like ionosphere, was applied together with the cross correlation coefficient method to a 7.0 magnitude earthquake that occurred in Mozambique on 23rd of February, 2006. Three Stations (two within the earthquake preparation zone) with hourly data of f0F2 for one month were used for the study. The results clearly revealed anomalies that are as a result of the earthquake. These were first noticed 10 days and another 3 days before the occurrence of this large earthquake.
Keywords:
ionospheric anomaly, geomagnetic Perturbations, Ionosphere, Hilbert-Huang transforms (HHT) and Cross correlation coefficient Method
Subject Areas: Atmospheric Sciences, Geophysics

1. Introduction
The interests in seismo-ionospheric coupling phenomena have increased in the last decade. The variations noticed in lithosphere, atmosphere and ionosphere parameters before the main earthquakes are considered as foreknowledge of impending earthquakes (earthquake precursors). However, the tendency of using these results to provide validly early warning for upcoming earthquakes is still considered somehow controversial [1] . The main reason for this can be attributed to the fact that the ionosphere is well known as a very complex and nonlinear system. Added to this is the fact that the variability in the ionosphere has several sources contributing to it. Therefore the main issue is distinguishing the variations caused by earthquake activities from those from other sources. The effects of the earthquake processes on the ionosphere can be investigated using both the ionospheric electron and/or ion densities. Perturbations noticed in the ionospheric plasma without any significant solar and geomagnetic disturbances may clearly be attributed to earthquakes sources [2] . These anomalies are seen in the E or F-layer and may be observed 1 - 10 days prior to the occurrence of the earthquake and also felt few days after it [3] . Statistical methods, being the main method use in the studies of seismo-ionospheric coupling, utilize ionospheric parameters like foF2 or TEC to analyze the ionosphere both before and after the earthquake. The main drive behind using these methods is to reveal any significant deviation of the chosen parameter of interest from its median value prior the seismic event [4] . The normalized equivalents of f0F2 or TEC are used, and this is normally done to eliminate the diurnal variation of foF2 or TEC [4] . However, the results clearly show that even though this technique ensures a more stable signal than the raw foF2 data, geophysical noise still exists in the signal, which will also affect the analysis. Another issue of note is that since variations caused by other sources such as ionospheric storms or geomagnetic perturbations may have contributions in the data, therefore, localizing the precursors will be difficult, if not totally obscured [3] .
Correlation analysis is a method which has been shown to address the problem of having to distinguish between geomagnetic storms and seismo-ionospheric precursors. This is due to the fact that geomagnetic storms produce more intense disturbances in the F2-layer (critical frequency) than earthquakes [5] . This analysis’ method utilizes f0F2 data before and after the occurrence of an earthquake from two carefully selected stations of the same period of time out of which one must be inside the earthquake preparation area, and the other one outside of it. The reasoning behind this is the fact that geomagnetic or ionospheric storms have global effects whereas the seismo-ionospheric coupling variations are localized within the earthquake preparation area [6] . In doing this, the two selected stations are expected to show the same effect from geomagnetic storms provided at least of course they are in the same (or close) latitude, leading to the correlation coefficient of the two station being high. However, correlation coefficient of the two stations will be low in the case of an earthquake since only one of the two stations will be within the earthquake preparation area [5] . However [5] added that for better results, the two stations should not differ too much in longitude, due to the local time dependence of the ionospheric variability caused by the magnetic storms. The earthquake used for this study occurred on the 23rd of February 2006 and it occurred near the southern end of the East African rift system. The East African rift system is a diffuse zone of crustal extension that passes through eastern Africa from Djibouti and Eritrea on the north to Malawi and Mozambique on the south and that constitutes the boundary between the Africa plate on the west and the Somalia plate on the east. At the earthquake’s latitude, the Africa and Somalia plates are spreading apart at a rate of several millimeters per year.
2. Hilbert-Huang Transform
Traditional data-analysis methods are all based on linear and stationary assumptions. Only in recent years have new methods been introduced to analyze non-stationary and non-linear data. For example, wavelet analysis and the Wagner-Ville distribution were designed for linear but non-stationary data [7] [8] . Additionally, various non-linear time-series-analysis methods were designed for nonlinear but stationary and deterministic systems [9] - [11] . Unfortunately, in most real systems, either natural or even man-made ones, the data are most likely to be both non-linear and non-stationary. Analyzing the data from such a system is a daunting problem. Even though challenging, new methods to examine data from the real world are certainly needed. A recently developed method, the Hilbert-Huang transform (HHT), by [12] - [14] seems to be able to meet some of the challenges. The purpose of HHT is to demonstrate an alternative method to present spectral analysis tools for providing the time-frequency-energy description of time series data. Also, the method attempts to describe non-stationary data locally. Rather than a Fourier or wavelet based transform, the Hilbert transform is use, in order to compute instantaneous frequencies and amplitudes thereby describing the signal more locally.
The HHT consists of two parts: empirical mode decomposition (EMD) and Hilbert spectral analysis (HSA). In Empirical Mode Decomposition, the signal is decompose into a series of structural components, known as Intrinsic Mode Functions (IMF). An IMF is defined as any function having the same number of zero-crossings and extrema. It also has symmetric envelopes defined by the local maxima and minima respectively [13] [15] . The second part of the method is just the Hilbert transform, which provides instantaneous frequencies as a function of time for each one of the IMF components. HHT has been tested and validated exhaustively, but only empirically. In all the cases studied, the HHT gave results much sharper than those from any of the traditional analysis methods in time-frequency-energy representations. Additionally, the HHT revealed true physical meanings in many of the data examined. Powerful as it is, the method is entirely empirical.
According to [16] , For a real signal x(t), the EMD starts by defining the envelopes of its maxima and minima using cubic splines interpolation. Then the mean of the two envelopes is calculated as
 (1)
(1)
Accordingly, the mean m1 (t) is then subtracted from the original signal
 (2)
(2)
and the residual h1(t) is examined as for the IMF criteria completeness. If it is an IMF then the procedure stops and the new signal under examination is the
 (3)
(3)
However, if h1(t) is not an IMF, the procedure, also known as “sifting”, is continued k times until the first IMF is realized.
Thus,
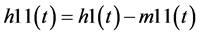 (4)
(4)
and finally
 (5)
(5)
The sifting process continues until the last residual is either a monotonic function or a constant. The final product is a wavelet-like decomposition going from higher oscillations to lower oscillations, which means that the frequency spectrum is decreased as the order of the IMF increases. In fact, with repeated siftings, the sifting process can recover signals representing low-amplitude riding waves.
The sifting process serves two purposes: To eliminate riding waves and to make the wave profiles more symmetric. While the first purpose must be achieved for the Hilbert transform to give a meaningful instantaneous frequency, the second purpose must also be achieved in case the neighboring wave amplitudes have too large a disparity. Toward these ends, the sifting process has to be repeated as many times as is required to reduce the extracted signal to an IMF.
3. Data Analysis
This study used foF2 data from the Grahamtown (Lat. 33.3S and Lon. 26.5E), Mandimo (Lat. 22.4S and Lon. 30.9E) and Louisvalle (Lat. 28.5S and Lon. 21.2E) ionospheric stations, made available by Space physic interactive data resource (SPIDR). The foF2 data are 1h sample recordings, around the time of the earthquake of magnitudes 7.0 (February, 23rd 2006). Data between 7th of February 2006 and 8th of March, 2006 (30 days or 720 hrs) were used for the study. Louisvalle station is the only station outside the earthquake preparation area, if the equation by [17] was applied. However, only Grahamtown station has a complete data while some days were missing in the other two stations. Mandimo station had only 358 hrs (From 362 to 720 hrs), while Louisvalle station had 455 hrs only (1 - 264, 481 - 672 hrs). This however did not stop certain facts about the coupling being revealed. This technique has not being tested for earthquake events in Africa before so this is probably the first application to an earthquake event.
4. Results
Two out of the three stations are within the earthquake preparation zone so both are expected to show the ionospheric precursors. One thing that was obvious is that the ionosphere over the Lousivalle station (Figure 1) around the time of f0F2 values available clearly showed a very different activity was going on when compared with the other Figures. The fact that almost all but very few hours before the earthquake were available made it
Figure 1. Initial f0F2 signal and the sifted signal of the Louisvalle station from 7th of February 2006 to 8th of March, 2006. With letter E as the hour of the earthquake.
difficult to say much about its pre-earthquake ionosphere. But hours after the earthquake clearly showed a different situation when compared with Figure 2 and Figure 3. From Figure 2, it is clear that there were gaps in the observation for 9 hrs (10 days before the earthquake) and for 15 hrs (the second day after the earthquake). However from the data available, Figure 3 (Grahamtown station) clearly showed gaps in the ionosonde observations first for 2 hrs (10 days before the earthquake), then for 3 hrs (3 days before the day of the earthquake), another for 12 hrs (on the day after the earthquake) together with another 5hrs the second day after the earthquake as seen as the blue gaps in the two figures. The fact that Figure 2 and Figure 3 are within the earthquake preparation area made it important that such vital details cannot be ignored. The exact time the gaps occurred in the observations can be seen in Table 1.
On the other hand, applying the cross correlation coefficient to Grahamtown and louisvalle stations together with Grahamtown and Madimo stations confirmed the seismo-ionospheric coupling. In Figure 4(a), the cross-correlation coefficient between the denoized foF2 signals was plotted for the period of 30 days, from February 7th to March 8th 2006 of Grahamtown and Madimo stations. The Figure showed a severe initial drop 10 days before the earthquake and also another drop also after the event. Figure 4(b) (Grahamtown and Louisvalle stations) showed a drop few days before and also after the event. Table 2 shows the characteristics of this earthquake.
5. Conclusions
This paper applied the Cross-Correlation Coefficient method, together with the Hilbert-Huang Transform, for the analysis of f0F2 around the time of an earthquake in Mozambique. Using the cross correlation coefficient method helps in eliminating from the data, disturbances in the ionosphere that might be of geomagnetic storms sources, thereby making visible variations that are considered too weak (caused by earthquake events) to be revealed. One of the things noted from Figures 1-3 is that even after four sifting processes, the signal only separated into positive and negative values as expected but however, maintained its original oscillatory mode. Being an IMF, it however has variable amplitudes as a function of time. Sifting process serves two purposes: To eliminate low-amplitude riding waves and to make the wave profiles more symmetric. While the first purpose must be achieved for the Hilbert transform to give a meaningful instantaneous frequency, the second purpose must also be achieved in case the neighboring wave amplitudes have too large a disparity [13] . What is clear therefore is that the data do not have too large disparity in the neighboring amplitudes. The fact that both stations within the earthquake preparation zone showed the gaps at the same time but of different length of time, together with the point that the station outside the zone showed no sign of it before or after the earthquake is of importance. [17] in their recent work showed that the occurrences of earthquakes do not always coincide with gaps in ionosonde observations. However, from the data available, the station (Mandimo) closer to the epicenter of the earthquake witnessed the gaps for a much longer time than the Grahamtown station revealed the fact that the gaps were of a localized source (seismogenic) and not a global one. This further confirms that the gaps were
Figure 2. Initial f0F2 signal and the sifted signal of the mandimo station from 7th of February 2006 to 8th of March, 2006. With letter E as the hour of the earthquake and the blue cap as the hours where the f0F2 were absent.
Figure 3. Initial f0F2 signal and the sifted signal of the Grahamtown station from 7th of February 2006 to 8th of March, 2006. With letter E as the hour of the earthquake and the blue cap as the hours where the f0F2 were absent.
Table 1. Shows the time of occurrence of the gaps in the ionosonde observations.


Figure 4. (a) Plot of the correlation coefficient of the denoised foF2 signals from Grahamtown and Mandimo correlation. Red arrow being the day of the earthquake; (b) Plot of the correlation coefficient of the denoised foF2 signals from Grahamtown and Louisvalle correlation. Red arrow being the day of the earthquake.
Table 2. Characteristics of the Mozambique earthquake.
ionospheric precursors to the large earthquake and it is in accordance with the results of previous seismo- ionospheric studies.
On the other hand, the fact that Grahamtown station is 976.1 km away from the epicenter of the earthquake and the mandimo station, 291.6 km away from the epicenter was responsible for the different time responses to the impending earthquake. It is assumed that a station very close to the circumference of the circle, that is, the theoretical estimation of the earthquake preparation area, may either detect the earthquake or not. [18] reported this phenomenon and attributed it to the complex distribution of the anomalous electric field as it penetrates the ionosphere.
Acknowledgements
Special appreciation goes to Space physic interactive data resource (SPIDR) for providing the data used for this paper.
Cite this paper
Enoch Oluwaseun Elemo, (2015) Cross Correlation Analysis of Mozambique’s 7.0 M Earthquake Using the Empirical Mode Decomposition. Open Access Library Journal,02,1-7. doi: 10.4236/oalib.1101184
References
- 1. Xu, T., Hu, Y., Wu, J., Wu, Z., Suo, Y. and Feng, J. (2010) Giant Disturbance in the Ionospheric F2 Region Prior to the M8.0 Wenchuan Earthquake on 12 May 2008. Annales Geophysicae, 28, 1533-1538.
http://dx.doi.org/10.5194/angeo-28-1533-2010 - 2. Silina, A.S., Liperovskaya, E.V., Liperovsky, V.A. and Meister, C.-V. (2001) Ionospheric Phenomena before Strong Earthquakes. Natural Hazards and Earth System Sciences, 1, 113-118.
http://dx.doi.org/10.5194/nhess-1-113-2001 - 3. Pulinets, S.A. and Boyarchuk, K.A. (2004) Ionospheric Precursors of Earthquakes. Springer, Berlin.
- 4. Pulinets, S.A. (1998) Seismic Activity as a Source of the Ionospheric Variability. Advance Space Research, 22, 903-906.
http://dx.doi.org/10.1016/S0273-1177(98)00121-5 - 5. Pulinets, S.A., Gaivoronska, T.B., Leyva Contreras, A. and Ciraolo, L. (2004) Correlation Analysis Technique Revealing Ionospheric Precursors of Earthquakes. Natural Hazards and Earth System Sciences, 4, 697-702.
http://dx.doi.org/10.5194/nhess-4-697-2004 - 6. Pulinets, S.A. (1998) Seismic Activity as a Source of the Ionospheric Variability. Advances in Space Research, 22, 903-906.
http://dx.doi.org/10.1016/S0273-1177(98)00121-5 - 7. Flandrin, P. (1999) Time-Frequency/Time-Scale Analysis. Academic Press, Cambridge, 386 p.
- 8. Gröchenig, K. (2001) Foundations of Time-Frequency Analysis. Birkhäuser, Switzerland, 359 p.
http://dx.doi.org/10.1007/978-1-4612-0003-1 - 9. Diks, C. (1999) Nonlinear Time Series Analysis: Methods and Applications. World Scientific Press, Singapore, 180 p.
http://dx.doi.org/10.1142/3823 - 10. Kantz, H. and Schreiber, T. (1999) Nonlinear Time Series Analysis. Cambridge University Press, Cambridge, 304 p.
- 11. Tong, H. (1990) Nonlinear Time Series Analysis. Oxford University Press, Oxford, 564 p.
- 12. Huang, N.E., Long, S.R. and Shen, Z. (1996) The Mechanism for Frequency Downshifts in Nonlinear Wave Evolution. Advances in Applied Mechanics, 32, 59-111.
http://dx.doi.org/10.1016/S0065-2156(08)70076-0 - 13. Huang, N.E., Shen, Z., Long, S.R., Wu, M.C., Shih, H.H., Zheng, Q., Yen, N.C., Tung, C.C. and Liu, H.H. (1998) The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proceedings of the Royal Society of London, Series A, 454, 903-995.
http://dx.doi.org/10.1098/rspa.1998.0193 - 14. Huang, N.E., Shen, Z. and Long, S.R. (1999) A New View of Water Waves: The Hilbert Spectrum. Annual Review of Fluid Mechanics, 31, 417-457.
http://dx.doi.org/10.1146/annurev.fluid.31.1.417 - 15. Huang, N.E., Wu, M.C., Long, S.R., Shen, S.S.P., Qu, W., Gloersen, P. and Fan, K.L. (2003) A Confidence Limit for Empirical Mode Decomposition and Hilbert Spectral Analysis. Proceedings of the Royal Society of London, Series A, 459, 2317-2345.
http://dx.doi.org/10.1098/rspa.2003.1123 - 16. Tsolis, G.S. and Xenos, T.D. (2009) Seismo-Ionospheric Coupling Correlation Analysis of Earthquakes in Greece, Using Empirical Mode Decomposition. Nonlinear Processes in Geophysics, 16, 123-130.
http://dx.doi.org/10.5194/npg-16-123-2009 - 17. Dobrovolsky, I.R., Zubkov, S.I. and Myachkin, V.I. (1979) Estimation of the Size of Earthquake Preparation Zones. Pure and Applied Geophysics, 117, 1025-1044.
http://dx.doi.org/10.1007/BF00876083 - 18. Pulinets, S. and Davidenko, D. (2014) Ionospheric Precursors of Earthquakes and Global Electric Circuit. Advances in Space Research, 53, 709-723.
http://dx.doi.org/10.1016/j.asr.2013.12.035





