Received 6 January 2015; accepted 22 January 2015; published 27 January 2015

ABSTRACT

Through reevaluating the physical significance of Hubble law, we propose the concept of spatial relativity and make two postulates: 1) Distance is equivalent to motion; 2) Hubble radius 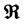is constant. Such an approach can help us to develop the theory of relativity into a unified form, and further construct a simple and consistent cosmological model. It shows that, our universe can be treated as an eternal 3-dimensional ball with an edge never reached served by the physical horizon, whose inherent geometrical property will directly lead to Hubble law, rather than Doppler mechanism. Importantly, the presented model can provide us a unified scheme to deal with the cosmological problems, but without employing more extra assumptions. This will greatly change our understanding of the cosmic spacetime.

Keywords:

Hubble Law, Hubble Radius, Spatial Relativity

Subject Areas: Theoretical Physics

1. Introduction

In 1929, Hubble announced his discovery in astronomical observation [1] , that is a proportional relation between spectral redshift of galaxies and their distance, called Hubble law (HL). HL assigned to the Doppler effect, seems always to lead to the idea of an expanding universe, and then the Big Bang model (BBM) established [2] - [4] . Although BBM has been accepted widely for succeeding in explaining many observational results, it still lacks a dependable basis. For example, BBM cannot interpret the beginning of time, the initial conditions of the universe, or why the Big Bang began in the first place [5] - [7] . In all the mentioned, the most worthy of attention is so-called horizon crisis [8] - [10] : why, as a dynamic whole, could the cosmic system contain many causally disconnected regions? The focus of the issue certainly lies in the Doppler mechanism of Hubble redshift, that is, as two different type involved quantities in usual kinematics, the cosmic distance r and Hubble velocity (HV, the recession velocity of celestial body) u_H need to obey different additions, but indeed they are also linked by the Hubble relation u_H = Hr (H Hubble constant). This means that, as long as H is constant, it would inevitably lead to the observational contradiction. Specially, if distance is doubled, the recession velocity determined by HL will be doubled (even greater than the speed of light c), u_H (2r) = Hr, whereas by the Lorentz velocity addition, due to the body at position 2r moving with a velocity Hr as measured in the cosmic rest frame S' at r, and the velocity of S' relative to the earth reference S reading Hr, it seems to be equal to.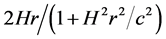

To avoid the contradiction, we raise HL to the status of a postulate, and stress the equivalence of distance and motion. It shows that, for being equivalent to motion, the cosmic distance should obey the same addition as velocity. Starting from this, we develop the theory of relativity into a unified form, in term of which spatial geometry, kinematics and cosmic electrodynamics are to be understood. The modified spatial geometry can help us to construct a static cosmological model with neither a beginning nor end of time, and hence no need to define initial conditions. In our model, the universe is appearing as a finite 3-dimensional ball of radius 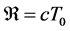(with cosmological time T₀ = H⁻¹), just corresponding to the physical horizon. The properties of the model are discussed and some new results are presented.

2. Unified Form of Relativity

Basic consideration. In cosmology, the cosmological principle is always regarded as a theoretical cornerstone [11] [12] , which emphasizes the universe should appear the same in every direction from every point. However, such a physical thought has not been carried out completely in BBM, since no rule is provided to determine how an event in one region is related to the same as measured in another causally disconnected region, whereas these regions were theoretically allowed to exist. This is a serious defection, we cannot accept it, just like we cannot accept an event occurring in one inertial frame is not physically allowed to be observed in the other.

To find the way out of the impasse, we extend the content of the relativistic principle: no experiment can definitely single out one of frames of reference is “truly” stationary or at “absolute” origin, while the others are “truly” moving or in the off position. This means the physical relativity is not only reflected in motion, but in space, namely the cosmic space has the relativity too. Therefore, the difficulty that had to be resolved amounted to choosing amongst two alternatives: 1) Distance and velocity obey different additions, and something was wrong with HL; 2) There is a new principle valid for cosmological observation. The first possibility should be thrown out due to many observational evidences supporting HL. The second is our final choice: physical laws are the same in every part of our universe, or, no experiment can detect the “absolute” position of a frame. Hereby, we make two postulates:

Postulate I. Physics in a still frame at position r in relativistic space is equivalent to physics in an inertial frame moving with velocity Hr in rigid space (i.e. Euclidean space).

Postulate II. Hubble radius 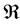is constant.

By the two, the cosmological and relativistic principles can be stated uniformly as that: the universe does not possess any privileged positions or frames. Once the idea is included in this framework, all the frames, whether in remote distance or motion, are now on equal footing. Importantly, 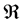must go into Einstein field equations (EFE): 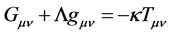(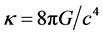) to play the role of cosmological constant, and this will greatly change our understanding of the spacetime geometry. Taking the observational value [13] of H = 2.4 × 10⁻¹⁸ s⁻¹, we get.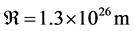

To illustrate the consequences of our postulates, we reassert that HV is only quantitatively equal to the velocity of a particle passing though distance r in time interval T₀, but indeed represents a virtual velocity for its being unable to cause any displacement. So that, if assuming there exists a kind of displacement 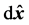to be responsible for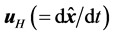, the spatial position can be defined as

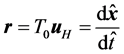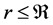, (1)

where 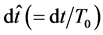denotes the time number. Constancy of allows us to construct an invariant quantity 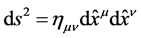(,the Minkowski metric), and further derive a Lorentz type

transformation with matrix determined by Lorentz factor. It tells us

that, two events observed by observer S' to be simultaneous (,), would be seen by observer S (far from S' with r) to occur at different times, namely simultaneity is also a spatial relative concept.

Accordingly, the transformation for 4-position gives the distance additions in parallel and vertical directions respectively

, (2)

This is a remarkable and general result, which in the case of, reduces to the usual form. Meanwhile, Equation (2) also presents that, if an object has a distance less than to one observer, its distance is always less than for any other observer, provided this other observer is at distance less than. In particularly, for two objects at the opposite sides of observer O with distance, BBM points that, due to laying outside of the each other’s respective horizons, one could not be observed in the other. However by Equation (2), the measured distance is only, and if, then, namely any celestial body at horizon from one observer will have the same distance in view of the other (see Figure 1). To understand physically why this is the case, it is necessary to turn to the consequences of spatial relativity.

Effects of spatial relativity. Until now, we have only concerned the spatial relativity, but need to look at its kinematics. The reason is that, according to the usual view if given a speed, an object will move without bound i.e. up to and then beyond the horizon range. This implies, if accepting the transformation above, it will transform a real position into imaginary. To avoid the problem, we must distinguish two type velocities in physics, the first is a virtual velocity, called HV, the second a real velocity, called displacement velocity (DV), and define the full velocity (FV) by.

Now, we emphasize only the frames of moving with constant FV relative to a free particle can be treated as the inertial ones, which would strongly suggest us to modify the Newton inertia law as that: the inertial nature of free moving object is no longer to keep usual velocity, but FV constant. Therefore, the spacetime geometry could be derived from the assumption that there exist rigid coordinates with two properties: 1) Two events, can be connected by a light signal if and only if; 2) Free particles obey the modified inertia law. As an example, for a free particle departing from the origin with velocity u, its DV reads, followed by and. When, , meaning the propagation speed of light will decay exponentially to zero, to ensure the horizon never to be crossed. Similarly, for a photon coming from the horizon, we have and, which gives. This does not lead to contradiction, for u_D representing the relative speed of photon flying away from the horizon, like the separation speed of two reverse motion photons. In fact, the FV of light measured by any observer in any position, without exception, is c.

What is the physics behind the spatial relativity? The answers are time dilation―a distant clock appears to run slow, and length contraction―a distant object appears to contract. Physically, to interpret time dilation, we consider a rest light clock of ticking away the time by light-pulse bouncing back and forth between proper length L₀ (see Figure 2). For a local observer, one has the duration of a round trip (proper time). To observer S with respect to whom the clock is at position r (in perpendicular), the light will traverse L₀ with DV

in time interval, showing time dilation.

Correspondingly, a length will get shortened in sight line when measured by a distant observer. Shown as Figure 3, placing the light clock in parallel, the duration for local observer is still Δt₀. Whereas for observer S, the pulse distance becomes L, and the total round time. Due to, and, , the length contraction is deduced,. This phenomenon is usually known as the Lorentz-Fitzgerald contraction, but here it is an observable spatial effect.

Developed relativistic principles. Now, it should be restated that, the universe appears the same in every direction from every point in FV space, and the statement encourages us to develop Einstein’s postulates as:

The principle of relativity Physical laws have the same form in all frames of reference moving with constant FV with respect to one another.

Constancy of FV of light. The FV of light is independent of the motion and position of its source.

The moving behavior of material objects will be influenced by, and consistent with the FV transformation between different frames. The transformation for 4-velocity gives

, (3)

which in the case of and, can directly lead to Hubble relation in 4-vector form.

Let us examine the point O' at position r in frame S, its proper distance should be for. If measuring in a frame with radial velocity u relative to S, we obtain. This rigid length determines a distance in relativistic space

(4)

when, it reduces to the usual length contraction. However, as, , meaning any moving observer will observe the same horizon(notice that, such the conclusion does not hold in BBM). And thus, the universal significance of developed relativistic principles is embodied.

For simplicity, we rewrite the 4-coordinate interval as (omitting the mark above), which gives the geodesic equation, requiring free particle keep its FV constant. To interpret the properties, we plot the r-t diagram, whose world line traces out the curve rather than straight line. Therefore, suppose an event O occurs at the origin, we find the world lines of the photons passing through will lie on a convex cone with a vertex at O, called lightcone (see Figure 4).

3. Dynamics

Relativistic Dynamics. As an extension of usual momentum, the FV 4-vector must satisfy two criteria: 1) It must be conserved in all observational positions for being compatible with cosmological principle; 2) It must reduce to the usual form as, requiring the relativistic laws to be correct in close enough range. The definition leads us to an idea of that the mass of particle will increase with r, until tend to infinite at the horizon, i.e.. Such relation for galaxies implies an observational fact that the massive galaxies look farther (form early), whereas low-mass galaxies look closer (form late) [14] . Moreover, when applying the transformation to a photon of wavelength coming from the object at r, its spectral shift as measured at the origin would be

(5)

This is very the Hubble relation.

For free particle, we can naturally think of its FV momentum conservation, namely. So that, if treating as the displacement momentum, we have

, (6)

The result shows, even for a free particle, it will be subjected to an effective damping force proportional to its DV, and finally tend to still to ensure it never cross the horizon. That is to say, any moving particle will bear an acceleration of, instead of uniform motion as the usual inertia law described. However in general, such deceleration is so small that the law is approximately valid. Moreover, for a stressed particle, its motion behavior could be described by the dynamic equation, which reduces to the usual relativistic form in local region.

An interesting step is to introduce the 4-momentum inertia, which suggests. It indicates that, the momentum of moving particle eventually represents a transfer ability of delivering mass m to position. When, , namely only photon can reach the horizon. On the other hand, we also see that, the energy of a moving body will finally convert into its energy inertia, but in turn, it does not be allowed to happen spontaneously. Such the moving irreversibility should be not ignored in physics, it perhaps heralds a strong unidirectional arrow of time governing everything that happens [9] . Nevertheless, the truly remarkable aspect of the above conclusions is that it has its fundamental origin in the fact that there exist the universal maximum possible speed and distance, the light speed and the Hubble radius, which are both built into the structure of spacetime.

Cosmic electrodynamics. It is natural that, the electrodynamics of moving bodies could be in agreement with the developed relativistic principles, under which all the problems in electrodynamics could be discussed. In particularly, when we say Maxwell equations (ME) are covariant, we eventually must specify the transform properties of the electromagnetic fields E and B. Namely, under the FV Lorentz transformation, not only the space and time coordinates will change, but also the electromagnetic fields. The transform formulae for ME are somewhat simpler when written in the Heaviside-Lorentz system of units, of which the rigid coordinate form is [15]

(7)

where denotes the 4-current densities. Correspondingly, the Lorentz force on charge q reads with. In above unit system, the transform properties of the electromagnetic fields are given by

(8)

Using these rules, we can check the covariance of equations of electromagnetism. The approach can provide us all the knowledge of cosmic electrodynamics, the key point is to transform the involved quantities into relativistic space. For example, by Equation (7) we get the Coulomb field, which in relativistic space becomes

(9)

for. It shows that, besides the usual Coulomb field, the charge also induces a resistant field. This is different from our traditional idea.

4. Relativistic Cosmological Model

In modern cosmology, our universe is described as a surface of 4-dimensional sphere, whose contracting or expanding in the direction of the 4-radius would give all the dynamical properties of cosmic system [16] . But here, we model our universe as an eternal 3-dimensional sphere with a never reached edge corresponding to Hubble radius, whose spatial coordinates plusing time can just form Minkowski metric. Therefore in our model, the flatness and horizon problems would naturally disappear, but without employing the expansion hypothesis, inflationary or otherwise [2] .

To introduce into EFE, we suppose a particle is placed at the origin of a small spherical space, within which the matter is removed (). Due to the ubiquitous fluctuation, the particle will obtain a small disturbed velocity, whose 4-vector form reads followed by. Now, if treating as the metric tensor with perturbation, we can calculate Einstein tensor, and find the cosmological constant should be. It suggests

(10)

In this way, is introduced into EFE as a natural constant.

Therefore, for our universe of with the stress-energy tensor of homogeneous and isotropic static ideal fluid, we have, and then

(11)

which requires, being 1/3 of the critical energy density given by BBM [16] . Physically, it is sensible, as long as constant, the system energy would be strictly proportional to its volume V, namely. When the volume changes, a amounts of work will be done. According to the energy conservation, there must be. Not only that, if treating the horizon term in Equation (11) as a contribution to the stress-energy tensor, , we can get an effective result. This zero stress-energy balance is the cause of the cosmic balance (i.e. ). Meanwhile, the covariant conservation of also yields and.

Now, by analogy with the modified Coulomb field (9), we write the Newtonian gravity in relativistic space as

(12)

From which we see that, accompanying with the usual gravity, there is always a repulsive field that could be responsible for the discoveries of gravitationally self-repulsive dark energy [17] [18] . And it is this repulsive field that maintains the balance of the Newton universe (). In particularly, we review the Newtonian gravity caused by mass within the sphere of radius r, that is. Correspondingly, the total repulsive effect from cosmic matter reads

(13)

It shows that, for the Newton universe, the widespread existence of repulsive interaction can just resist the gravitational collapse, namely. In the way, the dynamic balance is held.

By the transformation of volume element, we write the apparent number density of galaxies as, n₀ is the background mean number density near us. The total number of galaxies within radius r in relativistic space reads, just equal to that of uniform density n₀ within radius in rigid space. The analytical results of galaxy count reflect this trend, that is, the farther distance, the more galaxies [19] [20] . Similarly, the apparent energy density can be given by. Such a distribution may provide us with some analytical clues to the dark matter [21] .

Finally, Equation (5) also tell us the apparent variation of temperature of cosmic blackbody radiation with redshift, , is the temperature near us. But, this does not imply the existence of a low temperature cosmic center, because any observer at any position would see the same result. In 1997, Songaila et al. [22] investigated the topic, their measurement yielded. And by the presented, we have, in agreement with the observational result.

5. Summary

As presented above, BBM maintains the existence of the causally disconnected regions in cosmic space, and this is clearly contrary to the spirit of physical unification. Here, we show that, the difficulties can be overcome by proposing the sameness of distance and motion, and adopting instead a principle of relativity for cosmic mechanical and electromagnetic processes and by assuming the independence of the FV of light on the velocity and position of the source. Importantly, application of the developed principles can naturally lead to a detailed description of relativistic phenomena, and thus it can provide a consistent theoretical expression to the spatial geometry and material motion both at cosmological distance and in local space―all in a complete agreement with observations. This expression has numerous conceptual differences with the traditional ones, and thus possesses more explanatory power.

To sum up, our developments can be given as followings:

1) The starting point of this work is to propose the spatial relativity by raising the postulate status of HL, which would require the new spacetime geometry adapted to the modified inertia law.

2) A unified form of relativity theory has been derived from the FV relativistic principles: a) Physical laws have the same in all FV inertial frames; b) FV of light is constant. And the unified can give a satisfactory account of the phenomena of kinematics.

3) By the definition of 4-position (similar to that of 4-velocity), we have modeled our universe as an eternal finite 3-dimensional ball, where the cosmological phenomena will appear as consequences of the zero stress-energy balance in the structure.

Reviewing the overall scenario and its implications, what is most remarkable is that the developed theory will bring a significant change to physics. Especially, our cosmological model based on the concept of spatial relativity can differ so much from the standard picture, and lead to the current universe without employing more extra assumptions.

Cite this paper

Qiankai Yao, (2015) The Spatial Relativity and Its Physical Consequences. Open Access Library Journal,02,1-8. doi: 10.4236/oalib.1101286

References