Open Access Library Journal
Vol.02 No.01(2015), Article ID:68002,8 pages
10.4236/oalib.1101203
Gray Level Image Edge Detection Using a Hybrid Model of Cellular Learning Automata and Stochastic Cellular Automata
Nasim Vatani*, Rasul Enayatifar
Department of Computer, Firoozkooh Branch, Islamic Azad University, Firoozkooh, Iran
Email: *vatani_nasim@yahoo.com
Copyright © 2015 by authors and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 January 2015; accepted 18 January 2015; published 23 January 2015
ABSTRACT
The mathematical model that aims at determining points in an image at which the image brightness suddenly changes is called edge detection. This study aims to propose a new hybrid method for edge detection. This method is based on cellular learning automata (CLA) and stochastic cellular automata (SCA). In the first part of the proposed method, statistic features of the input image are hired to have primary edge detection. In the next step CLA and SCA are employed to amplify pixels situated on edge and castrate those pixels which are part of the image background. The simulation results are conducted to prove proposed method performance and these results suggest that the proposed method is more efficient in finding edges and outperforms the existing edge detection algorithms.
Keywords:
Cellular Learning Automata, Stochastic Cellular Automata, Edge Detection, Image Processing, Statistic Feature
Subject Areas: Artificial Intelligence, Image Processing

1. Introduction
The various applications in image processing, such as medical, military and engineering science, cause to promote techniques in feature extraction of image [1] . Derivation feature of digital image makes it easy to analyse image characteristics. Edge detection of digital image is one of the significant features, which is quite meaningful. Nowadays, numerous methods are considered for edge detection in image processing and machine vision, such as Sobel method [2] , gradient operator [3] [4] , edge detection with wavelet transform [5] - [8] , cellular automata (CA), cellular learning automata (CLA) and fuzzy cellular automata (FCA) [9] - [12] . Several well-known methods use first-order derivatives to estimate edge orientation [2] [13] . The main weakness of these methods is remaining the huge numbers of waste pixel in the input image after applying the algorithm, which causes the problem for detection real edges. Chang et al. [9] applied cellular automata for edge detection. This method worked based on some standard rule which was defined by authors. The problem of the mentioned method is the type of rules where all of them are constant with different sample images. Therefore, this deficiency makes algorithm dependent on input image. Most of these methods present in the past have a major deficiency; these are parametric for different edges dependent on a particular parameter. This parameter represents accuracy of edges. Although a number of algorithms have been developed for edge detection, it is still a challenging task to extract proper edges with desirable performance.
To have high quality edge detection method, an algorithm with four stages is employed. In the first stage standard deviation is calculated using Moore neighborhood [14] . Those edges which are extracted in this stage contain many waste pixels that should be removed. Then in the second step, an optimum function is employed to amplify the edge pixels and castrate those non edge pixels. The problem of this optimum function is that it keeps the same power for all pixels which makes some pixels blur. This defect will be solved in Stage 3 and Stage 4 where Stochastic Cellular Automata (SCA) and CLA are used, respectively. In fact, SCA are CA whose updating rule is a stochastic one, which means that the new entities’ states are chosen according to some probability distributions. It is a discrete-time random dynamical system [15] [16] . The CLA are the systems which have simple component, and behavior of each component is in the base of neighbor’s behavior and last experience of it [17] [18] .
This paper is divided into five parts. In Section 2, basic concepts of CLA and SCA and their structures are introduced. Section 3 discusses the proposed model and all details of the algorithm. The simulation results and comparison are presented in Section 4. Finally, the conclusion is derived in Section 5.
2. Preliminaries
In this section preliminaries information about learning automata (LA) and SCA will be defined.
2.1. Learning Automata
Narendra et al. [19] first introduced learning automata, which have been successfully employed in various applications. A learning automaton can be considered a decision-making unit situated in a stochastic environment that learns the optimal action through frequent interactions with the surrounding environment. An automaton is simply a set of a finite number of actions, where an action is randomly selected based on a specific probability distribution and applied to the environment. A reinforcement signal is sent back to the automaton based on evaluating the impact of the selected action. The automaton learning mechanism employs this feedback to update the existing action probability distributions. Repeating this action increases the probability distribution of better actions, and the most favorable or optimal action is eventually determined. Figure 1 presents the interaction process of automata and their environment.
Learning automata are represented by a four-tuple , where
, where 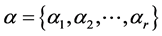 is a set of actions,
is a set of actions, 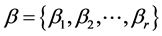 denotes a set of input actions,
denotes a set of input actions, 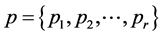 is a state probability vector and
is a state probability vector and 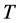 is a learning algorithm used to update the state probability vector:
is a learning algorithm used to update the state probability vector:
Figure 1. Interactions of learning automata and their environment.
After an automaton receives the reinforcement signal, it updates the state probability vector, applying Equation (1) for favorable response and Equation (2) otherwise.
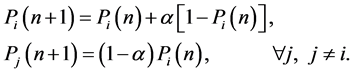 (1)
(1)
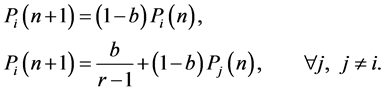 (2)
(2)
where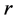 ,
, 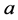 and
and 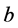 are the number of automaton actions, reward parameter and penalty parameter, respectively. An overview of the varieties of learning automata is presented by Thathachar and Sastry [20] .
are the number of automaton actions, reward parameter and penalty parameter, respectively. An overview of the varieties of learning automata is presented by Thathachar and Sastry [20] .
2.2. Stochastic Cellular Automata
Stochastic cellular automata locally interacting Markov chains [21] are an important extension of cellular automaton. Cellular automata are a discrete-time dynamical system of interacting entities, whose state is discrete. The state of the collection of entities is updated at each discrete time according to some simple homogenous rule. All entities’ states are updated in parallel or synchronously. Stochastic Cellular Automata are CA whose updating rule is a stochastic one, which means the new entities’ states are chosen according to some probability distributions. It is a discrete-time random dynamical system. From the spatial interaction between the entities, despite the simplicity of the updating rules, complex behaviour may emerge like self-organization. As mathematical object, it may be considered in the framework of stochastic processes as an interacting particle system in discrete-time.
3. Proposed Method
There are few edges in a uniform image, like image of the sea and there are many edges in image including many different objects. From statistical point of view it means standard deviation in image with the low number of edges is low and vice versa. The number of edges in each image can be determined with the help of this feature.
The proposed method is divided in to 3 main steps as follows:
Step 1: At first for each pixel, standard deviation is calculated using Moore neighborhood. This value is placed instead of pixel. This procedure is repeated for all pixels of image.
Step 2: After applying standard deviation, all detected edges have good quality; however the main weakness of this method is disability to remove the waste pixels from the background of image. To solve this problem, an optimum function is defined in Equation (3) to makes edges pixel stronger and background pixels weaker.
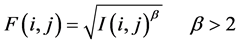 (3)
(3)
where 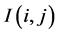 denotes the pixel in column
denotes the pixel in column 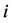 and row
and row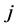 .
.
Normally, the value of 
Step 3: To improve the optimum function (Equation (3)) performance, value of 

Before defining rules, we assume that variable Similarity_Count save numbers of pixel in Moore neighborhood of each pixel which have same gray level with the central pixel. Mentioned rules are represented in Table 1. Third column shows the probability of belonging a pixel to edge.
Table 1. SCA rules.
To determine the value of 

where 
Step 4: In the last step of the proposed method our aim is to reinforce the edges pixel and remove the pixels which are belong to background. To obtain the mentioned goal a learning automaton with following rules is employed.
1) Dedicate a learning automaton with two actions (edge, non edge) to each pixel.
2) Each action initial probability is measured using Equation (5).

3) Action edge in each automaton will be awarded and action non edge will be punished if two rules were satisfied simultaneously:
a) Numbers of automaton in the Moore neighborhood of mentioned automaton which choose action edge are between 2 and 4.
b) Mentioned automaton chooses action edge.
In rest of states action edge will be punished and action non edge will be awarded.
4) The proposed method will be terminated if the entropy of two sequential stages is lower than the
5) Now, each automaton has its final action and if the action is edge the corresponding pixel is the part of edge and vice versa.
4. Experimental Results
In the current section, various experiments have been tested to identify and validate the proposed method’s performance.
4.1. Experimental Setup
A MATLAB 7 platform on a PC with an Intel Core i7, 2.3 GHz CPU, 8 GB memory and 500 GB hard disk with a Windows 7 Professional operating system is utilized to perform the introduced method. In this research all images are gray level with dimensions 

4.2. Testing Output of the Proposed Method
In the first experiment, the proposed method is applied on three images with dimension
4.3. Effect of 
In the second experiment, the effect of parameter 


4.4. Computational Time
In this experiment computational time of the four well-known edge detection methods are represented in Table 1. The results in Table 1 show the Sobel and Robet computational time are better than our proposed SCA-CLA method while SCA-CLA beat CNN-PSO in case of computational time. All the time in Table 2 is measured in millisecond (ms).
4.5. Comparison
To compare our proposed method with two basis edge detection methods namely Robert and Sobel [1] , the Peppers image is chosen as a test image where shows in Figure 4(a). Robert and Sobel edge detection methods are tested in Figure 4(a) and results are shown in Figure 4(b) and Figure 4(c), respectively. Figure 4(d) is the result when proposed method applied in Figure 4(a). The result clearly prove the superiority of our proposed method rather others well-known methods.




Figure 2. (a) Original images; (b) Standard deviation of images in the first row; (c) Apply SCA in images in row 2; (d) Apply CLA on images in row 3.


Figure 3. (a) Original image; (b) Standard deviation of original image; (c) Result image when


Figure 4. (a) Original image; (b) Robert edge detection; (c) Sobel edge detection; (d) Proposed method edge detection.
Table 2. Comparing the proposed method with others methods.
5. Conclusion
This paper conducted to present a new method for edge detection based on a hybrid model of cellular learning automata (CLA) and fuzzy cellular automata (FCA). In the first part of algorithm, standard deviation is applied to obtain the initial edges. Although in the second step an optimum function with the constant power is used to improve the edges quality, this power is constant for all the pixels and causes those non edge pixels to blur. To solve this problem, a hybrid model of SCA and CLA is used. The main advantage of the proposed method is using SCA and CLA for adjusting optimum function to reinforce edge pixels and castrate those non edge pixels. The numerical experiments and comparisons with the well-known existing methods justify the superior performance and efficiency of our proposed method.
Cite this paper
Nasim Vatani,Rasul Enayatifar, (2015) Gray Level Image Edge Detection Using a Hybrid Model of Cellular Learning Automata and Stochastic Cellular Automata. Open Access Library Journal,02,1-8. doi: 10.4236/oalib.1101203
References
- 1. Gonzales, R.C. and Woods, R.E. (1995) Digital Image Processing: Addison Wesley.
- 2. Ying-Dong, Q., et al. (2005) A Fast Subpixel Edge Detection Method Using Sobel-Zernike Moments Operator. Image and Vision Computing, 23, 11-17.
http://dx.doi.org/10.1016/j.imavis.2004.07.003 - 3. Sen, D. and Pal, S.K. (2010) Gradient Histogram: Thresholding in a Region of Interest for Edge Detection. Image and Vision Computing, 28, 677-695.
http://dx.doi.org/10.1016/j.imavis.2009.10.010 - 4. Zhang, Y., et al. (2014) The Modified Gradient Edge Detection Method for the Color Filter Array Image of the CMOS Image Sensor. Optics & Laser Technology, 62, 73-81.
http://dx.doi.org/10.1016/j.optlastec.2014.02.017 - 5. Tu, G.J. and Karstoft, H. (2015) Logarithmic Dyadic Wavelet Transform with Its Applications in Edge Detection and Reconstruction. Applied Soft Computing, 26, 193-201.
http://dx.doi.org/10.1016/j.asoc.2014.09.044 - 6. Zhang, H., et al. (2014) Improved Multi-Scale Wavelet in Pantograph Slide Edge Detection. Optik—International Journal for Light and Electron Optics, 125, 5681-5683.
http://dx.doi.org/10.1016/j.ijleo.2014.07.005 - 7. Zhang, X., Zhang, Y. and Zheng, R. (2011) Image Edge Detection Method of Combining Wavelet Lift with Canny Operator. Procedia Engineering, 15, 1335-1339.
http://dx.doi.org/10.1016/j.proeng.2011.08.247 - 8. Zheng, J., Peng, S.-P. and Yang, F. (2014) A Novel Edge Detection for Buried Target Extraction after SVD-2D Wavelet Processing. Journal of Applied Geophysics, 106, 106-113.
http://dx.doi.org/10.1016/j.jappgeo.2014.04.016 - 9. Chun-Ling, C., Yun-Jie, Z. and Yun-Yin, G. (2004) Cellular Automata for Edge Detection of Images. Proceedings of 2004 International Conference on Machine Learning and Cybernetics.
- 10. Enayatifar, R. and Meybodi, M.R. (2009) Adaptive Edge Detection via Image Statistic Features and Hybrid Model of Fuzzy Cellular Automata and Cellular Learning Automata. International Conference on Information and Multimedia Technology, Jeju Island, 16-18 December 2009, 273-278.
- 11. Patel, D.K. and More, S.A. (2013) Edge Detection Technique by Fuzzy Logic and Cellular Learning Automata Using Fuzzy Image Processing. Proceedings of the 2013 International Conference on Computer Communication and Informatics (ICCCI), Coimbatore, 4-6 January 2013, 1-6.
- 12. Gorsevski, P.V., Onasch, C.M., Farver, J.R. and Ye, X.Y. (2012) Detecting Grain Boundaries in Deformed Rocks Using a Cellular Automata Approach. Computers & Geosciences, 42, 136-142.
http://dx.doi.org/10.1016/j.cageo.2011.09.008 - 13. Canny, J. (1986) A Computational Approach to Edge Detection. IEEE Transactions on Pattern Analysis and Machine Intelligence, PAMI-8, 679-698.
- 14. Abin, A. and Beige, H. (2007) Edge Detection with Image Statistic Features and Cellular Learning Automata. Proceedings of the 13th Computer Conference, Tehran.
- 15. Garijo, N., Manzano, R., Osta, R. and Perez, M.A. (2012) Stochastic Cellular Automata Model of Cell Migration, Proliferation and Differentiation: Validation with in Vitro Cultures of Muscle Satellite Cells. Journal of Theoretical Biology, 314, 1-9.
http://dx.doi.org/10.1016/j.jtbi.2012.08.004 - 16. Chmura, T., Herz, B., Knorr, F., Pitz, T. and Schreckenberg, M. (2014) A Simple Stochastic Cellular Automaton for Synchronized Traffic Flow. Physica A: Statistical Mechanics and Its Applications, 405, 332-337.
http://dx.doi.org/10.1016/j.physa.2014.03.044 - 17. Mozafari, M. and Alizadeh, R. (2013) A Cellular Learning Automata Model of Investment Behavior in the Stock Market. Neurocomputing, 122, 470-479.
http://dx.doi.org/10.1016/j.neucom.2013.06.002 - 18. Torkestani, J.A. and Meybodi, M.R. (2011) A Cellular Learning Automata-Based Algorithm for Solving the Vertex Coloring Problem. Expert Systems with Applications, 38, 9237-9247.
http://dx.doi.org/10.1016/j.eswa.2011.01.098 - 19. Narendra, K.S. and Thathachar, M.A.L. (1974) Learning Automata: A Survey. IEEE Transactions on Systems, Man, and Cybernetics, SMC-4, 323-334.
http://dx.doi.org/10.1109/TSMC.1974.5408453 - 20. Thathachar, M.A.L. and Sastry, P.S. (2002) Varieties of Learning Automata: An Overview. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 32, 711-722.
http://dx.doi.org/10.1109/TSMCB.2002.1049606 - 21. Norris, J.R. (1998) Markov Chains. Cambridge University Press, Cambridge.
NOTES
*Corresponding author.






