Received 1 January 2015; accepted 18 January 2015; accepted 23 January 2015

ABSTRACT

Objective: The use of simulation in medical education has become an important and successfully implemented auxiliary method, recently. In this study, we aimed to present a compact screen- based computer simulation for second year medical students so that they may experience various aspects of peripheral nerve electrophysiology by themselves. Methods: The model used in the calculations combines both the passive and active membrane properties which were described in passive cable theory and in the classical study of Hodgkin and Huxley on membrane potential generation, respectively. Results: The simulation provides numerical and visual demonstration for various electrophysiological features of nerve cell such as membrane potential development, threshold stimulus, refractoriness, conduction in myelinated fiber, myelin and temperature effect on conduction etc. Besides, users may also have experience on propagation of compound nerve action potential that is the combined activation of nerve fibers. Conclusion: We suggest that this simulation may be considered as an auxiliary tool for classical physiology laboratory sessions. It is our intent to share and to make the simulation freely available to all interested readers.

Keywords:

Medical Education, Screen-Based Simulation, Compound Nerve Action Potential

Subject Areas: Anatomy & Physiology

1. Introduction

Medical students have direct contact with experimental animals and real patients during the certain phases of their education. Due to the bioethical limitations, animal experiments in laboratory sessions and practicing on patient may not always have learning outcomes, satisfactorily. Besides, these conventional methods may sometimes lead to practicing in an unsafe environment with some risk to either students or patients. It has been reported that in such cases the use of simulation has significant impacts on medical education if used in parallel with conventional methods [1] - [3] . Simulation studies span in the range from a simple three dimensional plastic model of isolated body parts to interactive and high-fidelity human patient simulators. The modern era of medical simulation starts from the second half of the 20^th century and uses electronic and computer technology, heavily [4] .

Based on the technological points of view, medical simulations can be evaluated in two categories [1] [3] [5] [6] . The applications belonging to the low level technology group still keep their importance in medical education mainly due to its lower cost. High technology simulation studies, on the other hand, have two main directions. The first is to help students in developing and improving their key skills through appropriate simulators before facing with real patients [6] . This sub-group is called “task trainers” and ranges from high-fidelity virtual reality simulators that replicate a clinical setting such as ultrasound, endoscopy, laparoscopic surgery, to microcontroller driven “realistic patient” simulators that may improve psychomotor skills, decision making, clinical problem solving, teamwork and communication skills.

The second direction consists mostly of low budgeted projects of basic medical sciences. In this group of simulations the solution of the mathematical model of a biological system/function is run on a computer screen, and user interactions are realized through the keyboard. Several samples of “screen-based” simulations in different areas of basic medical sciences can be found in the literature [4] [7] - [13] . They are all valuable resources within the context in which they are delivered. Some are for research purpose only; therefore, they are inappropriate for undergraduate students. The others either focused on a particular area of interest or give general perspective to paramedical students.

In this study we present a screen-based computer simulation program for the second year medical students. Through this simulation, we aimed to provide students with a simulator which gives a chance of experimenting on various aspects of nerve electrophysiology in a single compact computer program.

2. Method

Source codes of the simulation were written in Borland Delphi6 programming language for “Windows 98” or higher operating systems. Each sub-heading in question was presented on a different screen tab of visually enriched user friendly graphical interface. The sub-headings include developing resting and action potentials (AP) across the cell membrane, impulse conduction along a nerve fiber and propagation of compound action potential (CAP) in a peripheral nerve trunk. The simulation designed to let user exploring the effects of the following parameters on resting potential, AP and CAP:

1) Stimulus parameters

2) Ionic compositions of cellular fluids

3) Channel densities of cell membrane

4) Channel blocker applications

5) Temperature

6) Fiber diameter

7) Myelin thickness

8) Fiber diameter distribution

The constants and the initial values used in numerical calculations were chosen among the values that cold blooded animal have, in order for students to have comparable results in their “frog sciatic nerve action potential” laboratory session.

Description of the Underlying Model

Starting point of a CAP reconstruction is the AP generated in a single myelinated nerve fiber in response to a supra-maximal stimulus. The model for a propagating AP used in this simulation combines two models defined for different parts of a myelinated nerve fiber. The first one is the set of equations of Frankenhaeuser and Huxley [10] which represents AP generation/regeneration at the node of Ranvier. The other is the 2^nd order partial differential equation representing the electrotonic propagation of the membrane potential in the internode (passive cable theory) [14] . Combined electrical model of a typical myelinated fiber is given in Figure 1, schematically. Programming algorithms, assumptions, variables and constants used throughout the simulation are out of scope of this study and may be reviewed in relevant literatures by interested readers [9] [10] [14] [15] . For the readers’ convenience mathematical solutions for the corresponding electrical circuit model are given below;

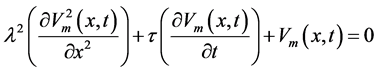(1)

(2)

Cable theory is mathematically solved for membrane potential V_m in time t and space x domain in Equation (1) where l and t are space and time constants defined for the internodal area, respectively. These constants were calculated numerically by using passive electrical properties of axonal membrane and myelin sheath. APs generated at nodes of Ranvier were calculated by Equation (2) which is the result of the classical study of Hodgkin and Huxley [9] . The equation calculates the total current I_m flowing through the membrane at Ranvier node in time domain. The equation intrinsically includes gating kinetics of channels (m, h, n gates) and equilibrium potential of main ions (E_Na, E_K, E_L). Myelination effect was added into the model by decreasing the thickness myelin sheath which in turn alters the equivalent capacitance (C_m) of myelin sheath [11] [14] .

Simulation solved both models simultaneously for fiber diameters between 2 to 20 µm and for successive 5 nodes (4 internodes). Numerical iterations were performed in 20 µs increments for temporal resolution, and in 2 mm for spatial resolution which was the initial assumption for fixed internodal length. CAPs were re-con- structed at 1, 2, 3 and 4 cm away from the stimulation site. CAP calculations were done based on the following main assumptions;

1) Axon diameters had only integer values between 2 - 20 μm;

2) Axon diameter did not change in axial direction;

3) Axon had a cylindrical shape;

4) Axons had equal contribution to CAP;

5) Ephaptic interactions between axons were neglected.

3. Results

User interface of the simulation consists of technically four screen tabs namely, “Resting Potential”, “Action Potential”, “Propagation” and “Compound Action Potential”. Each screen tab was designed to evaluate different perspectives of propagating electrical action of a nerve trunk.

3.1. Ionic Equilibriums and Resting Membrane Potentials

Nernst equilibrium potentials for the main ions and the generated resting membrane potential in response to a special ionic composition could be experienced graphically in the screen tab named “Resting Potential”. Users may explore logarithmic nature of the equilibrium potential by altering intra/extra cellular fluid’s ionic concentrations. Users may also correlate membrane potential with the change of maximum membrane conductance and concentrations of specific ions.

3.2. Action Potential and Refractoriness

In the screen tab called “Action Potential”, the change in membrane potential, AP at a Ranvier node is visualized in response to a stimulus. The relation between AP pattern and stimulus parameters, membrane properties and compartmental ionic composition could be experienced in this screen. Threshold stimulus assessment, all or none principle for AP, effects of ionic channel blockers (tetrodotoxin for Na⁺ channels and tetraethylammonium for K⁺ channels), temperature effects on AP and refractoriness issues in a myelinated fiber could also be studied in this screen tab. A sample scenario for a relative refractory period demonstration is presented in Figure 2.

3.3. AP Propagation and Demyelination

In the screen tab named “Propagation”, the propagation of an impulse in a myelinated axon is presented (Figure 3). Once an AP is generated at the initial node of Ranvier, it spreads into internodal area where myelin sheath covers axon membrane. While the membrane potential conducts passively towards the next node, the amplitude of the potential decreases. Amount of the decrease depends predominantly on the equivalent electrical properties of myelin sheath. If the membrane potential is still above threshold when it reaches the next node, AP is re-generated. Otherwise, conduction slowing or block occurs. This regenerative cycle was calculated for the 5 successive nodes and presented in the figure. Users may experience on the effect of myelin thickness on safety conduction (demyelination) in this screen tab by means of conduction velocities between nodes [11] [14] . User may also demonstrate the compensatory effect of low temperature on demyelination in this screen tab (Figure 4).

3.4. Compound Action Potential in Nerve Bundle

In last screen tab users may gain experiences on CAP reconstruction and propagation in a nerve trunk. In this screen tab of the simulation, user may adjust fiber diameter distribution parameters and recording distance in order to have certain scenarios, and observes the changes in CAP patterns. CAP patterns given in Figure 5 show decrease in amplitude, increase in duration, increase in latency and unchanged area under CAP signal as the recording distance increases.

4. Discussion

It is believed that any tools that improve the ability to examine, integrate, and understand physiological responses are indispensable in conveying some of the complex realities of modern medicine [16] . Simulations that put the user in a position of being the primary decision maker not to cause any stress on the user are accepted as successful tool [2] [4] . The simulation developed and presented in this study considers these objectives and provides platform for a screen-based teaching tool in the first two years of medical education. The program was designed to demonstrate specific learning objectives in excitable cell electrophysiology, interactively.

As it is in most simulation studies based on classical work of Hodgkin and Huxley [9] that intrinsically contains channel gating kinetics, this simulation covers the main features of simulated AP such as all or none rule, refractoriness, excitability, temperature effect, temporal summation and effects of channel blockers [2] [10] [12] [13] . Additionally, this simulation may also be used as a tool for understanding the underlying mechanisms of nerve conduction and conduction velocity slowing.

Internodal length was kept fixed in this simulation since the conduction velocity was found to be quite insensitive to nodal area and internodal length. However, it is sensitive to the capacitance of myelin sheath and axoplasmic conductance [17] [18] . Therefore, we may relate conduction velocity directly with myelin thickness. This variable, myelin thickness, was also used to define the severity of diffuse demyelination which alters the condition of safety conduction. Scenario given in Figure 3 shows delayed excitation in the neighboring node of Ranvier (RN 3) in the presence of myelin thickness of 3.4% of the normal. This is the critical level for safety conduction since AP completely diminished when myelin thickness was decreased to below this value which is consistent with literature [17] . Effect of lowering temperature on such a situation was observed as either an increase in conduction velocity (Figure 4) or restoration of conduction block [19] .

Because a nerve trunk comprises many axons having different diameter, it may consist of a wide range of conduction velocities. The pattern of CAP signals traveling along a nerve trunk may be affected by many factors; mainly, velocity dispersion, volume conductor effect and the ephaptic interactions between axons etc. [19] [20] . Considering that formation of CAP is a highly complex multi-factorial process, any simulation including this one, should be evaluated together with predefined assumptions. Our model depended on the standard set of generally accepted assumptions. These can be summarized as: 1) CAP can be represented as a linear superposition of its constituents which are single fiber action potentials; however, individual nerve fibers conduct action potentials independently and constantly, and 2) all fibers contributing to the CAP are activated simultaneously and instantaneously upon supra-maximal electrical stimulation [20] .

A sample of adjusted fiber diameter spectrum and corresponding CAPs traveling along the nerve trunk is given in Figure 5. Several CAP wave related parameters such as change in area under the wave, peak amplitude, and duration with respect to recording distance defined in the literature are in accordance with this simulation [21] [22] . Besides, understanding the general properties of CAP, this module may also give user the opportunity of correlating CAP patterns with certain type of peripheral nerve pathologies.

Among the many kinds of simulators being used in medical education, analog electromechanical simulators are very simple, cheap and also more educative than digital simulations for beginners [23] . However, if we want to simulate complex phenomena, choosing the digital simulation would be the only opportunity we have. Hence, we have developed a digital simulator to teach medical students the electrophysiological concepts of CAP originating from myelinated axons. There are of course several limitations in this simulation. Effects of Na/K pump and the currents through Ca⁺⁺ channels which are important under certain circumstances were not considered in potential generation across the axon membrane. It was supposed that only myelinated axons were arranged in tightly packed trunk and each had an equal contribution to CAP. Furthermore, the ephaptic interactions between axons along the nerve trunk were neglected.

This screen-based simulation has been used in our faculty for two years, and subjectively we have gathered positive student feedback. We suggest that this simulation may be considered as an auxiliary tool for related physiology laboratory sessions. It is our intent to share and to make the simulation freely available to all interested readers.

Cite this paper

Erhan Kiziltan,Nimet Unay Gundogan,Ayse Sebnem Ilhan,Leyla Aydin,Nuray Yazihan,Ferit Pehlivan, (2015) An Auxiliary Educational Tool for Propagating Single and Compound Nerve Action Potential. Open Access Library Journal,02,1-8. doi: 10.4236/oalib.1101288

References

NOTES

^*Corresponding author.