Open Access Library Journal
Vol.02 No.01(2015), Article ID:67978,10 pages
10.4236/oalib.1101255
Statistical Inferences Supporting the Hypothesis of Teaching with GeoGebra
Adrian Kllogjeri1, Pellumb Kllogjeri2
1Applied Econometrics, Kingston University, London, UK
2Department of Mathematics, University of Elbasan, Elbasan, Albania
Email: ad.kllogjeri@gmail.com, pkallogjeri@gmail.com
Copyright © 2015 by authors and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 December 2014; accepted 12 January 2015; published 16 January 2015
ABSTRACT
Our paper “Geogebra: A Global Platform for Teaching and Learning Math Together and using the Synergy of Mathematicians” [1] (published in the International Journal of Teaching and Case Studies (IJTCS), Vol. 2, 2010) presented the main advantages of using GeoGebra in the teaching and learning mathematics: easy teaching and easy learning, quick and correct grasping of the concept, and provision of an interactive learning environment. And above all, GeoGebra is an open source for teaching and learning for all. The purpose of this paper is to study and analyse of the effect of using GeoGebra software [2] in teaching and learning process of mathematics, and to support the advantage thesis related to it. We have investigated and got some conclusions whether the mathematical course taught by using GeoGebra software is as effective as more traditional methods of instruction. The results and the inferences are based on the experiment carried out in Albania, in a period of two years, in the second and the third year of several secondary schools of different cities. The scientific experimentation was the comparison of several groups, one of which served as a control group. The conclusions drawn at the end of the experiment are very optimistic. The test provides evidence that the new teaching and learning method in mathematics, based on GeoGebra software by using this software in teaching and learning process [3] , causes much more increase in the level of knowledge and skills in mathematics than the traditional method used in this process.
Keywords:
GeoGebra Software, Teaching with Technology, Scientific Experiment, ANOVA and Tukey Test
Subject Areas: Applied Statistical Mathematics

1. Introduction
A common form of scientific experimentation is the comparison of two groups. This comparison could be two different treatments: the comparison of a treatment to a control, or a before and after comparison. Our case is the comparison of the latter type. The preliminary results of experiments that are designed to compare two groups are usually summarized into a means or scores for each group. For the experimental class, they are the points (marks) collected from the previous chapter (in which the traditional method is used) and the points (marks) got by the students in the experimental chapter (in which GeoGebra software is used). For the control class, the same measuring units and chapters are applied with no difference in teaching method. In both chapters, the traditional method is used. GeoGebra is part of ICT (Information and Communication Technology) which is “a powerful change agent, ・・・, incorporates and extends the power of reading, writing, and arithmetic, ・・・, facilitates the automation of many mental activities” [4] (Introduction to Information and Communication Technology in Education, p. 6). GeoGebra is a special field to pursue research on teaching and learning and a strong tool to realize the “didactical triangle” which is “the teacher, the student, and the knowledge taught/learned” (Mathematics Education Library, 2002) [5] . The comparison will show or prove whether the observed differences between the two sets of data are real or just a chance difference caused by the natural variation within the measurements. A common way to approach that question is by performing a statistical analysis. The two most widely used statistical techniques for comparing two groups, where the measurements of the groups are normally distributed, are the Independent Group t-test and the Paired t-test. What is the difference between the two tests and when should each one be used?
For the normal distribution:
・ approximately 68% of the scores in the sample fall within one standard deviation of the mean;
・ approximately 95% of the scores in the sample fall within two standard deviations of the mean;
・ approximately 99% of the scores in the sample fall within three standard deviations of the mean.
Besides the normality assumption, another requirement of the Independent Group t-test is that the variances of the two groups should be equal. That is, if we are to plot the observed data from each of the two groups, the resulting bell-shaped histograms will have approximately the same shape. The numerical and graphical characteristics of data corresponding to the first experiment with two groups showed that the two samples (groups) under study were not bell-shaped, and that they had not a real normal distribution. This could be seen by the back to back histograms of data which were not normally distributed. However, they are just a sample. On the other side, by the experience it is reasonable to consider that the set of data consisting of the marks from the population of students has a normal distribution. Comparing the means of data of the test in the beginning of the chapter on derivatives and of data of the test at the end of the chapter on derivatives, they were 7 and 8.24, respectively. It is clear that there is a difference. Our purpose is to study the effect of using GeoGebra software in teaching and learning process, and investigate and determine whether the treatment with GeoGebra software in teaching and learning process causes a change in the individuals’ math knowledge and skills. We have to investigate and decide whether the mathematical course taught by using GeoGebra software is as effective as more traditional methods of instruction. Our testing hypothesis is related to the means of two methods of instruction: do two methods have the same mean?
In our case the subjects for the two groups are the same or matched. That is, the same subjects are observed twice: at the beginning of the chapter and at the end of it. The intervention, taking place between the two measures, is the use of GeoGebra software in teaching and learning mathematics.
In these conditions, the commonly used type of t-test is the Paired t-test. One advantage of using the same subjects is that experimental variability is less than the independent group case. For this test the mean difference between the two repeated observations is observed and compared. If the difference is sufficiently great, then there is evidence that the treatment (the new teaching and learning method) causes some change in the observed variable. The Paired t-test is performed and the observed difference between the groups is summarized in a p- value. The benefits of performing a t-test are that it is easy to understand and generally easy to perform. However, the fact that these tests are so widely used does not make them the correct analysis for all comparisons.
2. History of the Experiment
2.1. First Experiment and Results
First, confirm that you have the correct template for your paper size. This template has been tailored for output on the custom paper size (21 cm × 28.5 cm). The experiment was carried out in Elbasan, Albania, in the third year of a secondary school. The scientific experimentation was the comparison of two groups. Two classes were selected for the experiment. The experimental class was taught by the specialist of GeoGebra. The experimental chapter was the first chapter on Derivatives. The experimental class was taught using GeoGebra software whereas, the other class (control class) was taught in the traditional way by the same teacher. The control group appeared better than the experimental group at the beginning of the chapter. Its mean in the previous chapter was a little higher. In the first way for comparing the two groups at the end of the chapter we used the main statistics such as the mean and median of the two groups, also displaying their results (scores) with bihistogram and using box-plot. At the end of the chapter the experimental group showed to be better than the control one. This was the first evidence that teaching with GeoGebra is more effective than the traditional method of teaching.
Another way to compare the new method with the traditional one was by analyzing the paired observations (one done at the beginning of the chapter and the other at the end of the chapter). After summarizing the data into a means or scores for each group of results, which were the points (marks) collected from the previous chapter and the points (marks) got by the students in the experimental chapter, were compared the two sets of data of the experimental group. The compared data were the marks at the beginning of the chapter and the marks at the end of the chapter (chapter in which was used a new teaching and learning method in mathematics based on GeoGebra software). The assumption was that the set of data, consisted of the marks from the population of students, had a normal distribution (this was reasonable and acceptable by the experience regarding the distribution of the marks in the population of students). A paired t-test was performed and the observed difference between the groups was summarized in a p-value. Three types of questions regarding the true means, linked with the two methods of teaching, were:
1) Were the means from the two methods the same?
2) Was the mean of marks got by method of using GeoGebra software less (greater) than the mean of the marks got by traditional method?
These were “before” and “after” measurements with the scale on N objects, and the experiment was performed to decide whether there was a difference between “before” and “after” measurements.
The technique used: each “before” measurement was paired with the corresponding “after” measurement, and the differences 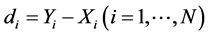 were calculated.
were calculated.
The idea if this technique is to do a comparison with an average increase in the level of mathematics of this group (in the same chapter) by using the traditional method one time and by using the GeoGebra teaching the second time. But, this is impossible because we have a state program for the schools that must be fulfilled and rigorously observed, so there was no room for repeating the chapter. For this reason, we used the average increase in the level of mathematics of the control group in this chapter where was used the traditional method. The paired sample t-test, the test statistic used to test for the difference of two means before and after a treatment, provided evidence that the new teaching and learning method in mathematics, based on GeoGebra software by using this software in teaching and learning process, causes much more increase in the level of knowledge and skills in mathematics than the traditional method used in this process. By the first test hypothesis “Was the mean of marks got by method of using GeoGebra software less (greater) than the mean of the marks got by traditional method?” was concluded that the new method of using GeoGebra software in teaching and learning math increases the level of math knowledge and skills over the traditional method. We are not giving the details of the first experiment here.
The test provided evidence that the new teaching and learning method in mathematics, based on GeoGebra software by using this software in teaching and learning process, causes much more increase in the level of knowledge and skills in mathematics than the traditional method used in this process.
2.2. Repetition of Experiment
The main reasons of repeating the experiment were:
1) In the first experiment the teacher of the experimental class was the experimenter as well;
2) The experiment was based on two classes only, so there was not sufficient evidence of drawing right and trusted conclusions.
Criterions for the selection of the classes in the repeated experiment:
1) The selection of the classes is based on the known relationships between the experimenters and the teachers and the availability and willingness of the teachers to be involved with the experiment;
2) The experimenter is not the teacher of the classes;
3) In the experiment are involved four classes;
4) The experiment is performed in the same chapter “Systems of equations and in equations”. This chapter is taught in the second year of the middle school;
5) The classes have not much difference in their means regarding the quality in math;
6) The classes have totally different backgrounds, coming from three different towns (Elbasan, Fier and Librazhd). The control class is from Elbasan. They have different teachers who are trained with GeoGebra and ex- perimenting for the first time the new method?teaching with GeoGebra. The groups are independent from one another. The experiment range is wider.
3. Methodology and Testing
3.1. ANOVA Test
Since our task was to compare the means of several groups (four) and get conclusion about which teaching and learning method is better we performed ANOVA test. One-way Analysis of Variance (ANOVA) is used when we want to compare more than two means. The statistic corresponding to ANOVA test is F-statistic (Fisher statistic) defined by the ratio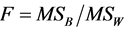 , where the nominator is the between-groups mean square and the denominator is the within-groups mean square [6] . In the ANOVA test, samples are drawn from each population and the data is used to test the null hypothesis that the populations are all equal against the alternative that not all are equal. The preliminary work, having all is needed to perform the test, is in the following table (see Table 1), containing all the by hand computations: the sample sizes, the sums, the sums of squares for each group, the means and the totals. The classes are labelled A, B, C and D. D is the control class. Next are the other figures necessary for the estimation of F-statistic, as shown in Table 2. Performing the F test one-way test (ANOVA) is used to test whether the means of all groups are equal. In the ANOVA test, samples are drawn from each population and the data is used to test the null hypothesis that the populations are all equal against the alternative that not all are equal. If we reject the null, we need to perform some further analysis to draw conclusions about which population means do differ.
, where the nominator is the between-groups mean square and the denominator is the within-groups mean square [6] . In the ANOVA test, samples are drawn from each population and the data is used to test the null hypothesis that the populations are all equal against the alternative that not all are equal. The preliminary work, having all is needed to perform the test, is in the following table (see Table 1), containing all the by hand computations: the sample sizes, the sums, the sums of squares for each group, the means and the totals. The classes are labelled A, B, C and D. D is the control class. Next are the other figures necessary for the estimation of F-statistic, as shown in Table 2. Performing the F test one-way test (ANOVA) is used to test whether the means of all groups are equal. In the ANOVA test, samples are drawn from each population and the data is used to test the null hypothesis that the populations are all equal against the alternative that not all are equal. If we reject the null, we need to perform some further analysis to draw conclusions about which population means do differ.
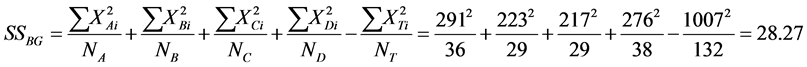
SSBG?Sum of Squares between Groups;
SSWG?Sum of Squares within Groups.
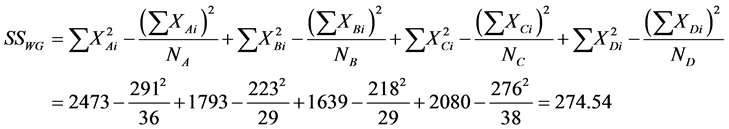
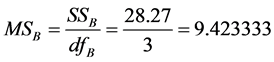
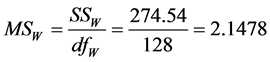

The summary table is:
Assumptions of the ANOVA and the test of null hypothesis:
1) The data is normally distributed;
2) The population standard deviations are equal.
In our experiment, the random variable, representing the marks, has approximately a normal distribution. It is confirmed by many statistical studies and this fact is considered in many text books. In many problems, the pop- ulation standard deviations are considered equal, but what we do with our experiment? Recall: Our second as-
Table 1. Table of the sample sizes and the sums.
Table 2. Summary table for F-statistic.
sumption of the ANOVA model was that our population standard deviations are all equal. The official test is quite complicated and not practical, also statistical official data do not help, so we use the following rule of thumb:
If the largest standard deviation is less than twice the smallest standard deviation we can use methods based on the assumption of equal standard deviations and our results will still be approximately correct. So we compare the quantity of 2 x smallest std. dev to the largest std. dev. Our concern is that 2 x smallest std. dev be greater than the largest std. dev. [6] .
The two hypotheses tested by ANOVA procedure are:
H0: 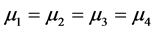 (all the means are equal);
(all the means are equal);
Ha: Not all the sample means are equal (at least one is different).
We have tested these hypotheses at three significance levels: α = 0.050, α = 0.025 and α = 0.010. The tabu-
lated values of , which are in accordance with the degrees of freedom of nominator and denominator of the ratio, taken out from the respective tables are:
, which are in accordance with the degrees of freedom of nominator and denominator of the ratio, taken out from the respective tables are:
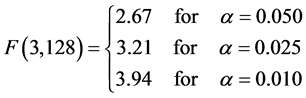
In the experiment carried out, the estimated value of F, called an F statistic, is 4.39 (look at the summary table, above). It tells us how much more variability there is between treatment groups compared to within treatment groups. The larger that ratio the more confident we feel in rejecting the null hypothesis, which is that all means are equal and the meaning is: there is no effect. As can be seen by Figure 1 of the probability density function for F, the estimated value of F falls in the three areas of rejection of H0 for the three levels of α. Therefore we reject H0 and accept Ha, concluding that the means of the four groups are not equal.
3.2. Test on the Means
Simultaneous Confidence Intervals for Differences between Means (Tukey’s test)
Although the ANOVA F test may be significant (i.e. we reject H0) it does not tell us specifically which means differ from each other. We can look at the difference graphically or by formal inference. We use the method of Simultaneous Confidence Intervals for Differences between Means (Tukey’s test). This method is used only after the rejection of H0 with the F test. All combinations of means are compared. Knowing that there are differences between the means, we naturally want to know which means are significantly different. This is post-hoc analysis. One of the post-hoc analyses, which is the most common choice, is the HSD (Honestly Significant
Figure 1. The graph of the probability density function for F (Exported by GeoGebra applet).
Difference) test of Tukey. Shortly, the HSD test is performed in the following way: is computed something analogous to a t-score for each pair of means, but they are not compared to the Student’s t-distribution. Instead, is used a new distribution called the studentized range or q-distribution [7] .
Caution: The post-hoc analysis is performed only if the ANOVA test shows a p-value less than chosen α. The p-value corresponding to the estimated F is less than each chosen α. If p > α, we don’t know whether the means are all equal or not, so we cannot be sure for unequal means. In our case, using the p-value calculator for the Fisher F-test, is found out that the p-value = 0.005628 which is much, much less than each chosen α [7] (Look at http://www.danielsoper.com/statcalc/calc07.aspx).
We want to know not just which means differ, but by how much they differ in order to see the effect size. The easiest thing is to compute the confidence interval first, and then interpret it for a significant difference in means. It is known that the relationship between a test of significance at α level and a 1 − α confidence interval is interpreted as follows:
・ If the endpoints of the CI have the same sign (they are both, positive or both negative), then 0 is not in the interval and we can conclude that the means are different;
・ If the endpoints of the CI have opposite signs, then 0 is in the interval but we can’t determine whether the means are equal or different.
The confidence interval can be computed similarly to the confidence interval for the difference of two means but using the q-distribution which avoids the problem of inflating α: since testing multiple hypotheses increases α dramatically. Even with just three treatments, the effective α is almost three times the nominal α. This is unacceptable. On the other side we cannot lower α for its decrease is associated with increase of β, which is chance of a Type II error. β represents the probability of a false negative, failing to find a difference in our means when there actually is a difference. This is unacceptable, too.
To test all the pairs of means at the same time, in one test, we extend the t-test to multiple samples, and that is called ANOVA. The confidence interval for each difference of paired means is:
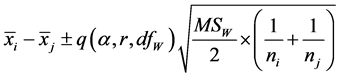
where 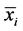 and
and 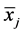 are the two sample means,
are the two sample means, 

The studentized range, developed by Tukey, overcomes the problem of inflating significance level [8] (look at Engineering Statistics Handbook, Nist/Sematech E-Handbook of Statistical Methods, http://www.itl.nist.gov/div898/ handbook/, Chapter 7: Product and Process Comparisons, 7.4.3.5. Confidence intervals for the difference of treatment means).
The assumptions of Tukey’s test:
1) The observations being tested must be independent;
2) The means come from normally distributed populations;
3) Observations have almost equal variations.
These assumptions in our case are met. The random variable, representing the marks, has approximately a normal distribution. It is confirmed by many statistical studies and this fact is considered in many text books [9] . The variances differ slightly from one another. The value of q is a function of the number of treatments, of the total number of data points and of α level. The estimation for the differences of the means and their respective confidence intervals is as in the following table (Table 3).
Explanation about the table:
1) The first column shows which group means are being compared;
2) The next column gives the point estimate of difference, which is the difference of the two sample means. The sample means of A and B are 8.08 and 7.69, so their difference is 0.39 and so on;
3) Third column relates to critical q. Looking at formula is understood that q (α, r, dfW) depends on the number of treatments and the total number of data points, not on the individual treatments, therefore it’s the same for all rows in any given experiment. In the experiment carried out in Albania regarding the effect of GeoGebra in teaching and learning math, there are four groups. Choosing

4) Fourth column contains the standardized error given from Tukey’s formula for confidence interval

In the experiment we are talking, the sample sizes are unequal, hence the standardized error varies when comparing different pairs of groups. For the first difference, A-B, we have:
5) Fifth column contains the two endpoints of the confidence interval computed for each difference by the formula:
Table 3. Differences of the means, critical q, SE and endpoints of the confidence interval.
6) The last column applies to the relation between confidence interval and significance test in order to see whether there’s a significant difference between the two groups. If the confidence interval includes the value 0, then that pair of means will not be declared significantly different, and vice versa. Looking at the difference of the means of groups A and D, that is A-D, the left endpoint of the interval is almost 0. Consequently, we don’t make a big mistake saying that the endpoints of the confidence interval are both positive. This means that 0 is not in this interval and we reject the null hypothesis of equality of the respective means (by noting YES in the respective row of that difference). In this table, only groups A and D have a significant difference.
Interpretation: The means of the groups A and D (the respective classes) are not equal. Moreover, the mean of the experimental class is greater than that of the control class and we are 95% confident that teaching with GeoGebra gives higher results than the teaching of the traditional way.
The confidence intervals of the other differences go from a negative to a positive, so they do include zero. That means that the two respective means might be equal or different, therefore we can’t say whether there is a difference between them. However, the interval center of each one is a positive number (0.9 approx.), leading us to say that there are differences. For each pair of the groups the tendency is the same. The effectiveness of the method “teaching with GeoGebra” is easily obvious when compare group A with group D. But, it is not so when we compare the groups B, C and D. We believe that one of the causes is the lack of experience of the teachers with GeoGebra software. The first experimental class (group A) is from Elbasan, a city in which there is more than 3-year experience using GeoGebra: training with teachers and diploma themes for the students of Elbasan University. The other two experimental classes are from schools of other towns where Geogebra was introduced and used for the first time during the experiment. Teachers themselves of these schools have faced difficulties in teaching with GeoGebra. Irrespective of such difficulties, the respective experimental classes have higher results (higher means) than that of the control class. In the experiment carried out during the year 2011 (March), the estimated value of F, called an F statistic which tells us how much more variability there is between treatment groups than within treatment groups, was in favor of Geogebra teaching. The larger that ratio, the more confident we feel in rejectingthe null hypothesis, which is that all means are equal implying that there is no effect. The test showed that the estimated value of F fell in the three areas of rejection of H0 for the three levels of α that were purposely chosen (look at Figure 1).
Although the ANOVA F-test may be significant, (i.e. we reject H0) it does not tell us specifically which means differ from each other. So, we looked at their differences using the method of Simultaneous Confidence Intervals for Differences between Means which is used only after the rejection of H0 with the F test. All combinations of means are compared.
The assumptions of Tukey’s test were met. The random variable, representing the marks, has approximately a normal distribution. The variances differ slightly from one another. Looking at the difference of the means of groups A and D, that is A-D (D is the control class), the left endpoint of the interval was almost 0. Consequently, 0 is not in this interval and we reject the null hypothesis of equality of the respective means. Table 3 shows that only groups A and D had a significant difference.
3.3. Problems, Lessons and Suggestions
The first problem regarding the results and inferences of the first experiment was the teacher of the experimental class. The experimenter was teacher of the class as well, so there are strong reasons of not believing the results and the inferences got at the end of the experiment. It is right to think that, in getting conclusions is not missing subjectivism.
・ Another questionable topic is: if there is a good positive difference between the results at the end of a chapter and the results at the end of the previous chapter, is this evidence that the improving scores are result of the new teaching and learning method? Our opinion is that the conclusions about the new method not be depended on this kind of comparison (by comparing the scores in different chapters).
・ The case of making comparison with an average increase in the level of mathematics of a class in the same chapter by using the traditional method one time and by using the GeoGebra teaching the second time cannot happen. This is impossible because we have a state program for the schools that must be fulfilled and rigorously observed, so there is no room for repeating the chapter. The other problem is that by repeating a second time the chapter it is expected and believed that the results must be higher (the results are correlated with the repetition process). For this reason, we used the average increase in the level of mathematics of the experimental group where was used “teaching with GeoGebra” and, of the control group (in the same chapter) where was used the traditional method.
・ The second (repeated) experiment showed again that the training of the math teachers with Geogebra [10] is very important for the implementation of “teaching and learning with GeoGebra” method in the teaching and learning process, also to draw right inferences about the experiment. The new method of teaching was based in one class only, in the first try, because of the lack of specialists in GeoGebra. The need of training the teachers was confirmed during the repeated experiment (much more in the other two towns where GeoGebra was introduced for the first time where no experience with GeoGebra was there).
・ The F-test: One-way test (ANOVA), used to test whether the means of several groups are equal, is more trustful than the t-test of any kind. The F-test is based on the measurements done in at least three groups (more many groups better the conclusions).
・ As mentioned above, the selection of the classes was based on the known relationships between the experimenter and the teachers and the availability and willingness of the teachers to be involved with the experiment. This is a violation of the important requirement and principal on randomness in carrying out the experiment. Therefore, when carried out an experiment special attention must be paid to the randomness (each member of the population must have the same chance of being member of the sample). In the case of experimenting with the teaching process must be thought well about what kind of test perform and how to independently select classes involved in the experiment. Our suggestion is that a good solution would be the cooperation with the ministry of Education and with the Regional Directorates of Education.
4. Conclusions
The results of the experiment carried out in Albania are positive and very promising. The experiment and the statistical tests confirm that:
・ The mathematical course taught by using GeoGebra software is as effective as more traditional methods of instruction;
・ The advantages of GeoGebra software are indisputable in the community of teachers and of specialists of mathematics;
・ The benefits of using GeoGebra software relate to independent and creative work, curiosity driving force, research opportunities, different science interactions, easy and better understanding of concepts, time benefit, wider and continually growing community of users, etc.
Inferences about the tests: The null hypothesis (all means are equal) was rejected, that is, the means of the classes were different. Hence we performed the Tukey’s test to know which means they differed and how much they differed in order to see the effect size. Looking at the confidence interval (Table 3) we observe that groups A and D have a significant positive difference, which means that the mean of class A is greater than that of D. Although for the other differences the ends of the intervals have not the same sign, we observe that the interval center of the differences B-D and C-D is a positive number (0.9 approx.). Using the probabilistic language, it means that the chance for the difference to be negative is 1/3 or less, whereas the chance to be positive is 2/3 or more, approximately. This fact leads us to say that there are differences between the experimental classes and the control class (D). It is more likely that the teaching with GeoGebra increases the class mean. Looking at differences A-B, A-C and B-C, we observe that the interval center moves from 0.3 to 0.4. The center is close to 0. There is no problem in this fact because in this case the experimental classes are compared.
Cite this paper
Adrian Kllogjeri,Pellumb Kllogjeri, (2015) Statistical Inferences Supporting the Hypothesis of Teaching with GeoGebra. Open Access Library Journal,02,1-10. doi: 10.4236/oalib.1101255
References
- 1. Pellumb, K. (2010) GeoGebra: A Global Platform for Teaching and Learning Math Together and Using the Synergy of Mathematicians. International Journal of Teaching and Case Studies, 2, 225-236.
- 2. Hohenwarter, J. and Hohenwarter, M. (2008) Introduction to GeoGebra. Online, 37-42.
- 3. Hohenwarter, J. and Hohenwarter, M. (2012) Introduction to GeoGebra4 (Modified). 114-124.
http://facultyfp.salisbury.edu/despickler/personal/Resources/GeoGebra_Guides/introen_4_2 - 4. David, M. (2005) Introduction to Information and Communication Technology in Education. University of Oregon, Eugene.
http://darkwing.uoregon.edu/~moursund/DigitalAge1/index.htm - 5. Mathematics Education Library (2002) Computer Environments for the Learning of Mathematics. Vol. 13, Kluwer Academic Publishers, New York, Boston, Dordrecht, London, Moscow, 191.
- 6. Spiegel, M.R. (1988) Statistics. 2nd Edition, McGraw-Hill, Book Company, 58-86.
- 7. http://www.danielsoper.com/statcalc/calc07.aspx
- 8. Engineering Statistics Handbook. Nist/Sematech, E-Handbook of Statistical Methods. Chapter 7: Product and Process Comparisons, Confidence Intervals for the Difference of Treatment Means.
http://www.itl.nist.gov/div898/ - 9. Goodman, A. (1995, 2003) Introduction to Data Col Lection and Analysis. Deakin University, location. Copyright © Deakin University, Chapter: Data Graphical Presentation.
- 10. Böhm, J. (2008) Linking Geometry, Algebra and Calculus with GeoGebra, ACDCA, DUG and Technical. University of Vienna, Vienna.





