Lossless compression of digital mammography using base switching method

doi:10.4236/jbise.2009.25049

Paper Menu >>

Journal Menu >>

J. Biomedical Science and Engineering, 2009, 2, 336-344

doi: 10.4236/jbise.2009.25049 Published Online September 2009 (http://www.SciRP.org/journal/jbise/

JBiSE

Published Online September 2009 in SciRes.http://www.scirp.org/journal/jbise

Lossless compression of digital mammography using

base switching method

Ravi kumar Mulemajalu1, Shivaprakash Koliwad2

1Corresponding author, Department of IS&E., KVGCE, Sullia, Karnataka, India; 2Department of E&C., MCE, Hassan, Karnataka, India.

Email: 1perajeravi@yahoo.com, 2spksagar2006@yahoo.co.in

Received 31March 2009; revised 15 May 2009; accepted 25 May 2009.

ABSTRACT

Mammography is a specific type of imaging that

uses low-dose x-ray system to examine breasts.

This is an efficient means of early detection of

breast cancer. Archiving and retaining these

data for at least three years is expensive, diffi-

cult and requires sophisticated data compres-

sion techniques. We propose a lossless com-

pression method that makes use of the

smoothness property of the images. In the first

step, de-correlation of the given image is done

using two efficient predictors. The two residue

images are partitioned into non overlapping

sub-images of size 4x4. At every instant one of

the sub-images is selected and sent for coding.

The sub-images with all zero pixels are identi-

fied using one bit code. The remaining sub-

images are coded by using base switching

method. Special techniques are used to save

the overhead information. Experimental results

indicate an average compression ratio of 6.44

for the selected database.

Keywords: Lossless Compression; Mammography

image; Prediction; Storage Space

1. INTRODUCTION

Breast cancer is the most frequent cancer in the women

worldwide with 1.05 million new cases every year and

represents over 20% of all malignancies among female.

In India, 80,000 women were affected by breast cancer

in 2002. In the US, alone in 2002, more than 40,000

women died of breast cancer. 98% of women survive

breast cancer if the tumor is smaller than 2 cm [1]. One

of the effective methods of early diagnosis of this type of

cancer is non-palpable, non-invasive mammography.

Through mammogram analysis radiologists have a de-

tection rate of 76% to 94%, which is considerably higher

than 57% to 70% detection rate for a clinical breast ex-

amination [2].

Mammography is a low dose x-ray technique to ac-

quire an image of the breast. Digital image format is

required in computer aided diagnosis (CAD) schemes to

assist the radiologists in the detection of radiological

features that could point to different pathologies. How-

ever, the usefulness of the CAD technique mainly de-

pends on two parameters of importance: the spatial and

grey level resolutions. They must provide a diagnostic

accuracy in digital images equivalent to that of conven-

tional films. Both pixel size and pixel depth are factors

that critically affect the visibility of small low contrast

objects or signals, which often are relevant information

for diagnosis [3]. Therefore, digital image recording

systems for medical imaging must provide high spatial

resolution and high contrast sensitivity. Due to this,

mammography images commonly have a spatial resolu-

tion of 1024x1024, 2048x2048 or 4096x4096 and use 16,

12 or 8 bits/pixel. Figure 1 shows a mammography im-

age of size 1024x1024 which uses 8 bits/pixel.

Nevertheless, this requirement retards the implemen-

tation of digital technologies due to the increment in

processing and transmission time, storage capacity and

cost that good digital image quality implies. A typical

mammogram digitized at a resolution of 4000x5000 pix-

els with 50-µm spot size and 12 bits results in approxi-

mately 40 Mb of digital data. Processing or transmission

time of such digital images could be quite long. An effi-

cient data compression scheme to reduce the digital data

is needed.

The goal of the image compression techniques is to

represent an image with as few bits as possible in such a

way that the original image can be reconstructed from

this representation without or with minimum error or

distortion. Basically image compression techniques have

been classified into two categories namely lossy and

lossless methods. Lossy compression methods cannot

achieve exact recovery of the original image, but

achieves significant compression ratio. Lossless com-

pression techniques, as their name implies, involve no

loss of information. The original data can be recovered

R. K. Mulemajalu et al. / J. Biomedical Science and Engineering 2 (2009) 336-344 337

Figure 1. A Mammography image of

size 1024x1024 which uses 8 bits/pixel.

exactly from the compressed data. In medical applica-

tions, lossless coding methods are required since loss of

any information is usually unacceptable [4]. Perform-

ance of the lossless compression techniques can be

measured in terms of their compression ratio, bits per

pixels required in the compressed image and the time for

encoding and decoding. On the other hand, since the

lossy compression techniques discard some information,

performance measure includes the mean square error and

peak signal to noise ratio (PSNR) in addition to the

measures used for the lossless compression.

Lossless image compression systems typically func-

tion in two stages [5]. In the first stage, two-dimensional

spatial redundancies are removed by using an image

model which can range from a relatively simple causal

prediction used in the JPEG-LS [6,7] standard to a more

complicated multi-scale segmentation based scheme. In

the second stage, the two-dimensional de-correlated re-

sidual which is obtained from the first stage, along with

any parameters used to generate the residual is coded

with a one-dimensional entropy coder such as the Huff-

man or the Arithmetic coder.

Existing lossless image compression algorithms can

be broadly classified into two kinds: Those based on

prediction and those that are transform based. The pre-

dictive coding system consists of a prediction that at

each pixel of the input image generates the anticipated

value of that pixel based on some of the past pixels and

the prediction error is entropy coded. Various local,

global and adaptive methods can be used to generate

prediction. In most cases, however the prediction is

formed by a linear combination of some previous pixels.

The variance of the prediction error is much smaller than

the variance of the gray levels in the original image.

Moreover, the first order estimate of the entropy of the

error image is much smaller than the corresponding es-

timate for the original image. Thus higher compression

ratio can be achieved by entropy coding the error image.

The past pixels used in the prediction are collectively

referred to as a context. The popular JPEG-LS standard

uses the prediction based coding technique [8]. Trans-

form based algorithms, on the other hand, are often used

to produce a hierarchical or multi-resolution representa-

tion of an image and work in the frequency domain. The

popular JPEG-2000 standard uses the transform based

coding technique [9].

Several techniques have been proposed for the loss-

less compression of the digital Mammography. A.

Neekabadi et al. [10] uses chronological sifting of pre-

diction errors and coding the errors using arithmetic

coding. For the 50 MIAS (Mammography Image Analy-

sis Society) images, CSPE gives better average com-

pression ratio than JPEG-LS and JPEG-2000. Xiaoli Li

et al. [11] uses grammar codes in that the original image

is first transformed into a context free grammar from

which the original data sequence can be fully recon-

structed by performing parallel and recursive substitu-

tions and then using an arithmetic coding algorithm to

compress the context free grammar. Compression ratio

achieved is promising but it involves more complicated

processing and large computation time. Delaunay trian-

gulation method [12] is another approach. It uses geo-

metric predictor based on irregular sampling and the

Delaunay triangulation. The difference between the

original and the predicted is calculated and coded using

the JPEG-LS approach. The method offers lower bit rate

than the JPEG-LS, JPEG-lossless, JPEG2000 and PNG.

A limitation is the slow execution time. Lossless

JPEG2000 and JPEG-LS are considered as the best

methods for the mammography images. Lossless JPEG

2000 methods are preferred due to the wide variety of

features, but are suffered from a slightly longer encoding

and decoding time [13].

Recently, there have been a few instances of using

segmentation for lossless compression. Shen and Ran-

gayyan [14] proposed a simple region growing scheme

which generates an adaptive scanning pattern. A differ-

ence image is then computed and coded using the JBIG

compression scheme. Higher compression ratio is possi-

ble with such a scheme for the high resolution medical

images. But the application of the same scheme to nor-

mal images did not result in significant performance

improvement. Another scheme reported in literature in-

volves using a variable block size segmentation(VBSS)

to obtain a context sensitive encoding of wavelet coeffi-

cients, the residual being coded using a Huffman or

Arithmetic coder [15,16]. The performance of the

method is comparable to that of the lossless JPEG stan-

dard. Mar wan Y. et al. [17] proposed fixed block based

(FBB) lossless compression methods for the digital

mammography. The algorithm codes blocks of pixels

within the image that contain the same intensity value,

thus reducing the size of the image substantially while

encoding the image at the same time. FBB method

alone gives small compression ratio but when used in

conjunction with LZW it provides better compression

338 R. K. Mu lemajalu et al. / J. Biomedical Science and Engineering 2 (2009) 336-344

ratio.

We propose a method based on Base switching (BS).

Trees-Juen Chuang et al. [18] have used Base-switching

method to compress the general images. [19] And [20]

also have used the same concept for the compression of

digital images. The algorithm segments the image into

non overlapping fixed blocks of size nn and codes the

pixels of the blocks based on the amount of smoothness.

In the proposed work we have optimized the original BS

method for the compression of mammography images.

Specific characteristics of mammography images are well

suited for the proposed method. These characteristics in-

clude low number of edges and vast smooth regions.

The organization of the paper is as follows. Section 2

describes the basic Base Switching (BS) method. The

proposed algorithm is given in Section 3. Experimental

results and conclusion are given in Sections 4 and 5 re-

spectively.

2. BASE-SWITCHING ALGORITHM

The BS method divides the original image (gray-level

data) into non-overlapping sub-images of size nn



Given a sub-image A, whose N gray values are

g0,g1,…gN-1 , define the “minimum” m, “base” b and the

“modified sub-image “AI, whose N gray values are

I,g1

I,…gI

N-1, by

nn 

gm min (1)

1minmax  ii ggb (2)





nn nnnn

AmI (3)

Also, for all i=0 to N -1 (4)

mgg i

i

where N=and each of the elements of I is 1. The

value of ‘b’ is related to smoothness of the sub-image

where smoothness is measured as the difference between

maximum and minimum pixel values in the sub-image.

nn 

The number of bits required to code the gray values gi

I is,

B = (5)



log



Then, total bits required for the whole sub-image is,

Z = N  bits. (6)



log

For example, for the sub-image of Figure 2, n=4,

N=16, m=95& b=9. Modified sub-image of Figure 3 is

obtained by subtracting 95 from every gray values of A.

For the sub-image in Figure 3, since B=4, =64 bits.

95 96 97 99

96 97 103 103

97 96 96 103

96 96 97 103

Figure 2. A sub-image A with n=4, N=16,

m=95, b=9& B=4.

012 4

128 8

211 8

112 8

Figure 3. Modified sub-image AI.

In order to reconstruct A, value of B and m should be

known. Therefore encoded bit stream consists of m, B

and AI coded using B bits. In the computation of B, If

b is not an integer power of 2, log2 (b) is rounded to the

next higher integer. Thus, in such cases, higher number

of bits is used than absolutely required. BS method uses

the following concept to exploit this redundancy.

It is found that, min gi

I=0 and max gi

I=b-1 (7)

The image AI = ( g0

I,g1

I,…,gI

N-1

) can be treated as an

N digit number (g0

Ig1

I…gI

N-1) b in the base b number

system. An integer value function f can be defined such

that f (AI,b)= decimal integer equivalent to the base-b

number.

= (8)









ibg

=g0

I+g1



b+…….+gI

N-1 bN-1 (9)

Then, number of bits required to store the integer f (AI,

b) is

Z= (10)







N

log

Reconstruction of AI is done by switching the binary

(base 2) number to a base b number. Therefore, recon-

struction of A needs the value of m and b. The format of

representation of a sub-image is as shown below.

Min. value in

the n



n block.

(8 bits)

Value of b

For the nn

block

(8 bits)

f (AI, b) coded using

Z bits

( bits)

For the example of Figure 3, b=9 and therefore

=51 bits. It is easy to prove that always B



. W



know that, Maximum value of f (AI, b) =b N1. -

Total number of bits required to represent f in binary is

Z== (11)







N

log



bN 2

log

Always,





bN 2

log





N  (12)



log



This verifies that AB ZZ



(13)

2.1. Formats Used for Encoding

Original BS algorithm uses a block size of 3x3 for seg-

R. K. Mulemajalu et al. / J. Biomedical Science and Engineering 2 (2009) 336-344 339

mentation. There are three formats used by the original

algorithm for encoding the sub-images.

Format1:

If b{1,2 …,11}, then the coding format is

1 bit

7 bits

8 bits

Binary equivalent of f (AI, b)

ZB bits

This format is economical when b<2 3.4

Format2:

If b (12, 13,…., 128}, then the coding format is

(1 bit)

(7 bits)

m(8

bits)

P(min,

max)

(7 bits)

Binary equivalent of

min max





gfor i

ii ii

(bits)

log





Here P(min,max) is a pair of two 3 bit numbers in-

dicating the position of minimum and maximum values.

If b>11, writing the positions of minimum and maximum

values is economical than coding them.

Format 3:

If b (129, 130,…., 256}, then the coding format is

(1 bit)

The original nine gray values: g0,g1,…g8

(72 bits)

Here, c stands for the category bit. If c is 0, then the

block is encoded using Formats 1 or 2; otherwise Format

3 is used.

2.2. Hierarchical Use of BS Technique

The encoded result of Subsection 2.1 can be compressed

further in a hierarchical manner. We can imagine that

there is a so-called “base-image”, whose gray values are

b0, b1, b2, …, b255; then, since it is a kind of image

(except that each value is a base value of a sub-image

rather than a gray value of a pixel), we can use the same

BS technique to compress these base values. The details

are omitted. Besides b, the minimal value m of each

block can also be grouped and compressed similarly. We

can repeat the same procedure to encode b and m values

further.

3. PROPOSED METHOD

In the proposed method, we made following modifica-

tions to the basic BS method.

1) Prediction

2) Increasing the block size from 3x3 to 4x4

3) All-zero block removal

4) Coding the minimum value and base value

3.1. Prediction

After reviewing the BS method, it is found that number

of bits required for a sub-image is decided by the value

of base ‘b’. If ‘b’ is reduced, the number of bits required

for a sub-image is also reduced. In the proposed method,

prediction is used to reduce the value of ‘b’ significantly.

A predictor generates at each pixel of the input image the

anticipated value of that pixel based on some of the past

inputs. The output of the predictor is then rounded to the

nearest integer, denoted

and used to form the dif-

ference or prediction error

nnn xxe  (14)

This prediction error is coded by the proposed entropy

coder. The decoder reconstructs from received code

words and perform the reverse operation

nnn xex  (15)

The quality of the prediction for each pixel directly

affects how efficiently the prediction error can be en-

coded. The better this prediction is less is the informa-

tion that must be carried by the prediction error signal.

This, in turn, leads to fewer bits. One way to improve the

prediction used for each pixel is to make a number of

predictions then chose the one which comes closest to

the actual value [21]. This method also called as

switched prediction has the major disadvantage that the

choice of prediction for each pixel must be sent as over-

head information. The proposed prediction scheme uses

two predictors and one of them is chosen for every block

of pixels of size 4x4. Thus, the choice of prediction is to

be made only once for the entire 4x4 block. This reduces

the amount of overhead. The two predictions are given

in Eq.16 and 17, in that, Pr1 is the popular MED pre-

dictor used in JPEG-LS standard and Pr2 is the one used

by [5] for the compression of mammography images.

For the entire pixels of a block of size 44, one of the

two predictions is chosen depending on the smoothness

property of the predicted blocks. Here, smoothness is

measured as the difference between maximum and

minimum pixel values in the block. The predictor that

gives the lowest difference value will be selected for that

block. The advantage here is that the overhead re-

quired for each block is only one bit.

otherwise. C-BA

B). (A,min C if B) (A,max Pr

B). (A,max C if B) (A,min









(16)





)1.02.02.01.03.01.0(Pr2



















FEDCBA

(17)

Here, A, B, C, D, E and F are the neighbors of pixel in-

volved in prediction as depicted in Figure 4.

The proposed switched prediction is described in the

equation form in 18 where d1 and d2 are the differ-

340 R. K. Mulemajalu et al. / J. Biomedical Science and Engineering 2 (2009) 336-344

C B E F

A X

Figure 4. Neighbors of pixel in-

volved in prediction.

ences between maximum and minimum values for the

two blocks obtained using the two predictors Pr1 and Pr2

respectively.

Pr = Pr

1 if d1<d2 (18)

= Pr2 otherwise

Figure 5 illustrates the prediction technique. It

shows two error images which are obtained by using

two predictors Pr1 and Pr2 respectively. The BS algo-

rithm divides them into 4x4 sub-images and computes

the difference between maximum and minimum pixel

values for all the four sub-images. For the first

sub-image, difference ‘d1’ is 6 and ‘d2’ is 8, where d1

and d2 are the differences of the sub-images corre-

sponding to the predictors Pr1 and Pr2 respectively.

Now, since d1<d2, the prediction Pr considers 4x4

sub-image of predictor Pr1 for further processing. This

procedure is repeated for all the other sub-images. The

resulting error image is shown in Figure 6. We use a

separate file predict to store the choice of predictor

made at every sub-image.

Figure 5. Prediction technique.

3.2. Increasing the Block Size from 3x3 to 4x4

It is obvious that smaller block size gives lower b value

but at the cost of increased overhead for the total image.

The basic BST algorithm uses a block size of 3x3 to

achieve optimum balance between amount of overhead

and compression efficiency. Since the prediction in-

creases smoothness, a larger block size can be chosen

without significant difference in the smoothness. Cer-

tainly, this will improve the compression ratio. We have

tested the proposed algorithm using different block sizes

and found that block size of 4x4 gives the best result.

This is supported by Table 1 giving the average com-

pression ratios obtained for the 50 mammography im-

ages for various block sizes.

3.3. All-Zero Block Removal

Mammography images are highly correlated so that pix-

els inside most of the sub-images are same. During pre-

diction and subtraction they have the highest chance of

becoming zeros. If a sub-image of the error image has all

its pixel values as zero, then that is marked as an all-zero

block by storing a bit 1 in the encoding format. For each

of the remaining sub-images, bit 0 is stored in the en-

coding format and is retained for further processing.

Mammography images of MIAS data-set shows very

large amount of all-zero blocks. This is supported by

Table 2 showing average number of all-zero blocks pre-

sent in the 50 mammography images of the MIAS dataset.

For these images, total bits required for marking the

presence or absence of all-zero blocks is 65536, since

Figure 6. Resulting error image.

Table 1. Average compression ratio obtained for various block sizes.

Table 2. Average number of all-zero blocks present in the 50

MIAS images.

3x3 4x4 4x8 8x4 8x8

6.18 6.44 6.15 6.18 5.92

Image size No. of blocks

of size 4



Average no. of

all-zero blocks

Remain-

ing blocks

1024



102465 536 32 282 33 254

R. K. Mulemajalu et al. / J. Biomedical Science and Engineering 2 (2009) 336-344 341

total sub-images are 65536. The error image will have

both negative and positive pixel values since the predic-

tion has changed the range of the pixel values from [0,

255] to [-255, 255]. Therefore, 9 bits are required to re-

cord the pixel values. The approximate average com-

pression ratio obtained by all-zero block removal for the

50 MIAS images considered in Table 2 can be estimated

by the following formula.

codingfor used pixelper bits block per pixels blocks remaining 65536

8 1024 1024





CR

9 16 33254 65536

8 10241024





=1.73.

into sub-images of size 4x4.The sub-images are then

processed one by one. For each sub-image, we have to

determine whether it belongs to all-zero category and if

so they are removed. The remaining blocks are retained

for further processing.

Here the value 65536 indicates the overhead bits re-

quired for marking the presence or absence of all-zero

blocks. The numerator gives total bits used by the origi-

nal uncompressed image. This computation clearly

shows that removal of all-zero blocks alone gives an

approximate compression ratio of 1.73. The two binary files zero and predict are separately

run length encoded, grouped and Huffman encoded.

Also, the two four bit files min and base are combined to

form an eight bit file and Huffman encoded.

3.4. Coding the Minimum Value and the

Base Value

The error image will have both negative and positive

pixel values. The prediction has changed the range of the

minimum value from [0,255] to [-255,255]. Therefore, 9

bits are required to record the minimum value. By

studying various images, it is found that minimum val-

ues are ranging from -128 to 64. More concentration is

observed between -8 to 0. Similarly, base values are

concentrated in the range 1 to 15. This statistics is sup-

ported by Table 3 of average number of minimum val-

ues and base values for the 50 mammography images.

3.6. Decoding a Sub-Image

Following are the decoding steps:

1) The files min, base, zero and predict are recon-

structed.

2) The decoding algorithm first checks whether the

block is an all-zero block or not. If all-zero, then a 4x4

block of zero’s is generated.

3) Otherwise, base value and minimum value are first

obtained by using the files min and base. The modified

image AI is reconstructed as explained in Section 2 and

4x4 error image is obtained by adding min value to it.

To exploit this redundancy, we use a typical categorize

and coding technique. A four bit code is used to identify

the minimum values. Minimum values less than 1 and

greater than -15 are given with codes 0 to 14, whereas

other minimum values are represented by the code 15

followed by their actual 9 bit values. A scheme similar to

this can be used to code the base values also. Base val-

ues between 1 and 15 are identified by using 4 bit codes

whereas values greater than 15 are identified using the

code 15 followed by their actual 9 bit values. The two

four bit codes for each of the sub-images are combined

to get an 8 bit number. Such 8 bit numbers are stored in a

file and Huffman encoded at the end.

4) Type of prediction used is read from the predict file.

The prediction rule is applied to the 4x4 error image and

the original 4x4 sub-image is reconstructed.

4. RESULTS

We evaluated the performance of the proposed scheme

using the 50 gray-scale images of the MIAS dataset that

include three varieties of images: Normal, Benign and

Malignant. The MIAS is a European Society that re-

searches mammograms and supplies over 11 countries

with real world clinical data. Films taken from the UK

national Breast Screening Program have been digitized

to 50 micron pixel edge and representing each pixel with

an 8 bit word. MATLAB is the tool used for simulation.

All the simulation was conducted on a 1.7GHZ proces-

sor and was supplied with the same set of 50 mammog-

raphy images. Each mammogram has a resolution of

1024x1024 and uses 8 bits/pixel. Results of the proposed

method are compared with that of the popular methods.

Comparison of Compression results for the 50 MIAS

images is shown in Table 4. This set includes all the

three varieties of images namely normal, benign and

malignant.

3.5. System Overview

As shown in Figure 7, we first divide the error image

Table 3. Average number of minimum and base values in 50

MIAS images.

Average No. of

minimum and

base values

Average no. of mini-

mum values in the

range -14 to 0

Average no. of

base values in

the range 1 to 15

33 253 32 466 33 097

JBiSE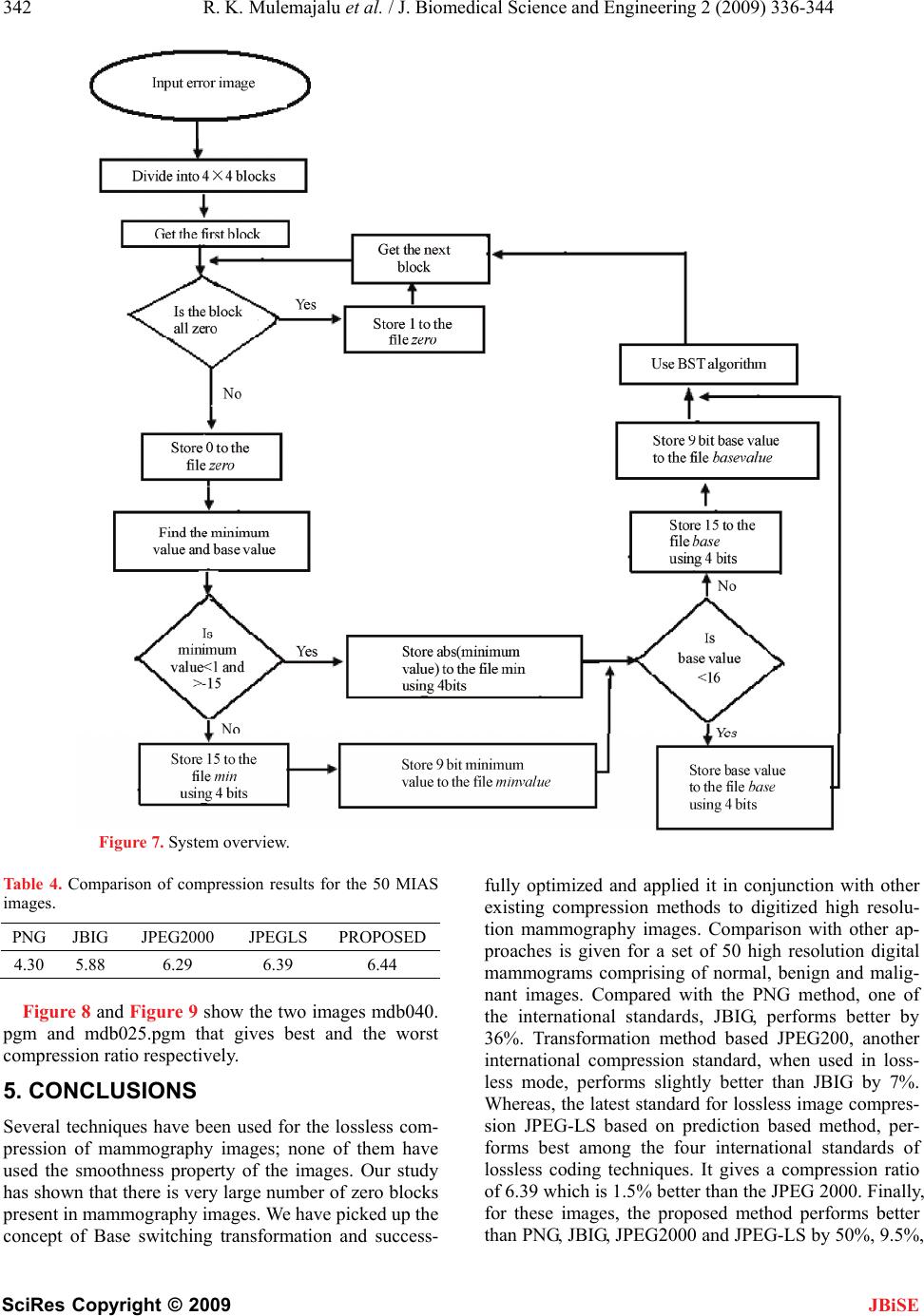

342 R. K. Mulemajalu et al. / J. Biomedical Science and Engineering 2 (2009) 336-344

Figure 7. System overview.

Table 4. Comparison of compression results for the 50 MIAS

images.

PNG JBIG JPEG2000 JPEGLS PROPOSED

4.30 5.88 6.29 6.39 6.44

Figure 8 and Figure 9 show the two images mdb040.

pgm and mdb025.pgm that gives best and the worst

compression ratio respectively.

5. CONCLUSIONS

Several techniques have been used for the lossless com-

pression of mammography images; none of them have

used the smoothness property of the images. Our study

has shown that there is very large number of zero blocks

present in mammography images. We have picked up the

concept of Base switching transformation and success-

fully optimized and applied it in conjunction with other

existing compression methods to digitized high resolu-

tion mammography images. Comparison with other ap-

proaches is given for a set of 50 high resolution digital

mammograms comprising of normal, benign and malig-

nant images. Compared with the PNG method, one of

the international standards, JBIG, performs better by

36%. Transformation method based JPEG200, another

international compression standard, when used in loss-

less mode, performs slightly better than JBIG by 7%.

Whereas, the latest standard for lossless image compres-

sion JPEG-LS based on prediction based method, per-

forms best among the four international standards of

lossless coding techniques. It gives a compression ratio

of 6.39 which is 1.5% better than the JPEG 2000. Finally,

for these images, the proposed method performs better

than PNG, JBIG, JPEG2000 and JPEG-LS by 50%, 9.5%,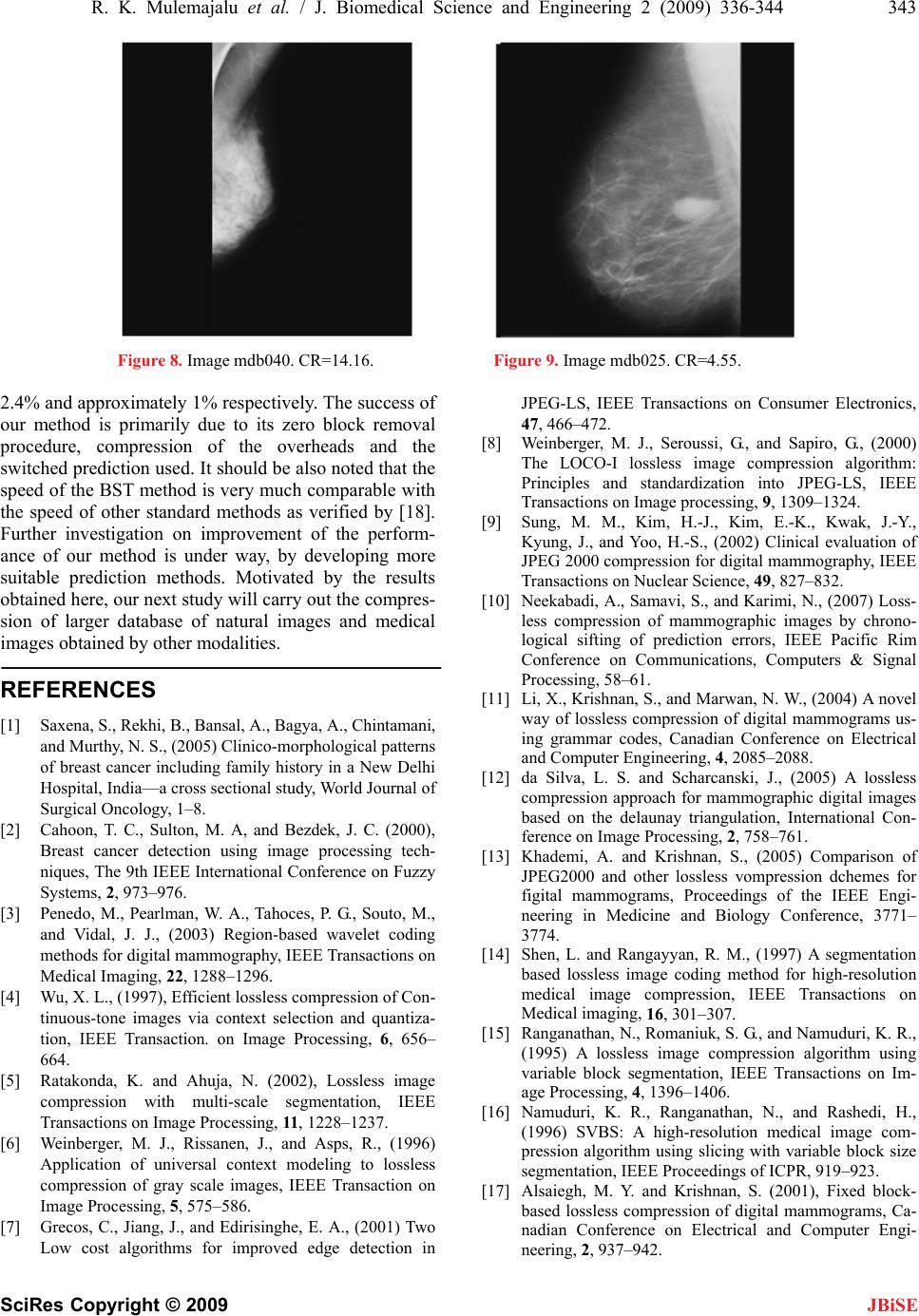

R. K. Mulemajalu et al. / J. Biomedical Science and Engineering 2 (2009) 336-344 343

Figure 8. Image mdb040. CR=14.16. Figure 9. Image mdb025. CR=4.55.

2.4% and approximately 1% respectively. The success of

our method is primarily due to its zero block removal

procedure, compression of the overheads and the

switched prediction used. It should be also noted that the

speed of the BST method is very much comparable with

the speed of other standard methods as verified by [18].

Further investigation on improvement of the perform-

ance of our method is under way, by developing more

suitable prediction methods. Motivated by the results

obtained here, our next study will carry out the compres-

sion of larger database of natural images and medical

images obtained by other modalities.

REFERENCES

[1] Saxena, S., Rekhi, B., Bansal, A., Bagya, A., Chintamani,

and Murthy, N. S., (2005) Clinico-morphological patterns

of breast cancer including family history in a New Delhi

Hospital, India—a cross sectional study, World Journal of

Surgical Oncology, 1–8.

[2] Cahoon, T. C., Sulton, M. A, and Bezdek, J. C. (2000),

Breast cancer detection using image processing tech-

niques, The 9th IEEE International Conference on Fuzzy

Systems, 2, 973–976.

[3] Penedo, M., Pearlman, W. A., Tahoces, P. G., Souto, M.,

and Vidal, J. J., (2003) Region-based wavelet coding

methods for digital mammography, IEEE Transactions on

Medical Imaging, 22, 1288–1296.

[4] Wu, X. L., (1997), Efficient lossless compression of Con-

tinuous-tone images via context selection and quantiza-

tion, IEEE Transaction. on Image Processing, 6, 656–

664.

[5] Ratakonda, K. and Ahuja, N. (2002), Lossless image

compression with multi-scale segmentation, IEEE

Transactions on Image Processing, 11, 1228–1237.

[6] Weinberger, M. J., Rissanen, J., and Asps, R., (1996)

Application of universal context modeling to lossless

compression of gray scale images, IEEE Transaction on

Image Processing, 5, 575–586.

[7] Grecos, C., Jiang, J., and Edirisinghe, E. A., (2001) Two

Low cost algorithms for improved edge detection in

JPEG-LS, IEEE Transactions on Consumer Electronics,

47, 466–472.

[8] Weinberger, M. J., Seroussi, G., and Sapiro, G., (2000)

The LOCO-I lossless image compression algorithm:

Principles and standardization into JPEG-LS, IEEE

Transactions on Image processing, 9, 1309–1324.

[9] Sung, M. M., Kim, H.-J., Kim, E.-K., Kwak, J.-Y.,

Kyung, J., and Yoo, H.-S., (2002) Clinical evaluation of

JPEG 2000 compression for digital mammography, IEEE

Transactions on Nuclear Science, 49, 827–832.

[10] Neekabadi, A., Samavi, S., and Karimi, N., (2007) Loss-

less compression of mammographic images by chrono-

logical sifting of prediction errors, IEEE Pacific Rim

Conference on Communications, Computers & Signal

Processing, 58–61.

[11] Li, X., Krishnan, S., and Marwan, N. W., (2004) A novel

way of lossless compression of digital mammograms us-

ing grammar codes, Canadian Conference on Electrical

and Computer Engineering, 4, 2085–2088.

[12] da Silva, L. S. and Scharcanski, J., (2005) A lossless

compression approach for mammographic digital images

based on the delaunay triangulation, International Con-

ference on Image Processing, 2, 758–761.

[13] Khademi, A. and Krishnan, S., (2005) Comparison of

JPEG2000 and other lossless vompression dchemes for

figital mammograms, Proceedings of the IEEE Engi-

neering in Medicine and Biology Conference, 3771–

3774.

[14] Shen, L. and Rangayyan, R. M., (1997) A segmentation

based lossless image coding method for high-resolution

medical image compression, IEEE Transactions on

Medical imaging, 16, 301–307.

[15] Ranganathan, N., Romaniuk, S. G., and Namuduri, K. R.,

(1995) A lossless image compression algorithm using

variable block segmentation, IEEE Transactions on Im-

age Processing, 4, 1396–1406.

[16] Namuduri, K. R., Ranganathan, N., and Rashedi, H.,

(1996) SVBS: A high-resolution medical image com-

pression algorithm using slicing with variable block size

segmentation, IEEE Proceedings of ICPR, 919–923.

[17] Alsaiegh, M. Y. and Krishnan, S. (2001), Fixed block-

based lossless compression of digital mammograms, Ca-

nadian Conference on Electrical and Computer Engi-

neering, 2, 937–942.

344 R. K. Mulemajalu et al. / J. Biomedical Science and Engineering 2 (2009) 336-344

[18] Chuang, T.-J. and Lin, J. C., (1998) A new algorithm for

lossless still image compression, Pattern Recognition, 31,

1343–1352.

[19] Chang, C.-C., Hsieh, C.-P., and Hsiao, J.-Y., (2003) A

new approach to lossless image compression, Proceed-

ings of ICCT’03, 1734–38.

[20] Ravikumar, M. S., Koliwad, S., and Dwarakish, G. S.,

(2008) Lossless compression of digital mammography

using fixed block segmentation and pixel grouping,

Proceedings of IEEE 6th Indian Conference on Com-

puter Vision Graphics and Image Processing, 201–206.

[21] Sayood, K., (2003) Lossless compression handbook,

First edition, Academic Press, USA, 207–223.