Journal of Environmental Protection, 2011, 2, 828-839
doi:10.4236/jep.2011.26094 Published Online August 2011 (http://www.SciRP.org/journal/jep)
Experimental and Numerical Investigation of
Desalination Plant Outfalls in Limited Disposal
Areas
Mohamed E. Abou-Elhaggag1*, Mohamed H. El-Gamal1, Mohamed I. Farouk2
1Faculty of Engineering, Cairo University, Giza, Egypt; 2Faculty of Engineering, Ain Shams University, Cairo, Egypt.
Received May 19th, 2011; revised June 21st, 2011; accepted July 25th, 2011.
ABSTRACT
In this study, experimental and numerical investigations of the dense brine jets are conducted for disposal areas of lim-
ited extent. First, a new experimental model representing a section of sea floor with a single port brine outfall is built to
study different characteristics of dense jets. Second, a number of numerical experiments have been conducted via Flu-
ent CFD package to compare the numerical results with its corresponding physical observations and measurements.
Experimental observations are made for both the terminal height of rise of dense jets discharged vertically from circu-
lar outlets into calm and homogeneous environment and for concentration profiles along the dense jet trajectory. Vari-
ous combinations of port diameters and concentration of effluent salinities are investigated to cover a wide range of
conditions. The results from the carried out experiments are compared to different available experimental and field
observations from the literature. A new model for the terminal height of rise of dense jets has been derived. The ex-
perimental observations of concentrations along the dense jet trajectory are analyzed to quantify the mixing patterns
for a given operating condition from the source point to the terminal height of rise. The numerical model has been used
to identify the penetration depth and also to get the temporal variation of the brine breakthrough curves at different
locations above the disposal port. The numerical model has shown the existence of multipeak breakthrough curves for
the farest points from the port (but the closest to the water free surface).
Keywords: Desalination, Dense Jets, Plumes, Terminal Height, Densimetric Froude Number, Fluent
1. Introduction
Due to the limited fresh water resources in many coun-
tries all over the world, desalination industry has been
widely flourished within its countries. It is expected that
the global desalinated water supply will reach 54 billion
m3 per year by 2020 [1]. It has been also noted that 24%
of the world desalination capacity occurs in Saudi Arabia.
Moreover, the Middle East houses the largest reverse
osmosis facility in world.
All desalination processes involve three liquid streams:
the saline feedwater stream (brackish or seawater), the
low-salinity product water, and the very saline concen-
trate (brine or reject water) stream. A by-product of de-
salination is brine which is a concentrated salt solution
(with more than 35 000 mg/1 dissolved solid) that must
be disposed of; generally by discharge it into deep saline
aquifers or into oceans or seas via outfalls.
For seawater desalination plants, it seems natural and
practical to dispose their brine waste back to the sea, via
marine outfalls at some distance from the shoreline [2].
Marine outfalls are considered the most feasible option
for brine disposal from seawater desalination plants due
to their reduced implementation uncertainty, well-sup-
ported technology, minimized land take, ability to moni-
tor and control, minimized maintenance and operation
fess [3]. The marine outfall might be surface discharge,
or single port outfall or multiport diffusers. Modern,
large capacity plants require submerged discharges, in
form of a negatively buoyant jet, that ensure a high dilu-
tion in order to minimize harmful impacts on the marine
environment [4].
The impact of brine disposal operations on coastal and
marine environment is still largely unknown; however, it
is commonly thought that the brines discharged must
ultimately be diluted and transported before disposed to

Experimental and Numerical Investigation of Desalination Plant Outfalls in Limited Disposal Areas829
the sea. Nevertheless, for each coastal seawater desalina-
tion plant, care has always been taken to determine the
optimum site of water intakes and brine waste outfalls.
Brine disposal has the potential to degrade the physical,
chemical and biological characteristics of the receiving
water body [5]. The degree of degradation is highly de-
pendent on the total volume of the brine being released,
its characteristics, the dilution rate prior to discharge, and
the characteristics of the receiving waters. The effect of
the brine on the environment is also highly dependent on
the geometric installation of the discharge outfall. Sev-
eral studies have shown the effect of the brine disposal
on the biophysical coastal environment [6-9]. Therefore,
it is important to understand how brine is dispersed into
the sea, so that we can minimize its potential environ-
mental impact.
Many experimental and field studies were conducted
to study the hydraulics of dense jets and plumes related
to the outfalls of the desalination plants, especially the
determination of the terminal height of rise, jets trajec-
tory, and concentrations profiles. The pioneer study by
[10] who investigated experimentally the jets in stagnant
fluids with different inclination angles of 30˚, 45˚, 60˚,
and 90˚ above the horizontal. Further experimental stud-
ies by [11-13] investigated jet trajectories and mixing
under both stagnant and flowing conditions. In more re-
cent experiments, [14] have investigated the 30˚, 45˚ and
60˚ configuration limiting the measurements to jet tra-
jectories without consideration of dilution values. All
these studies predict only near-field (initial mixing until
impingement with boundary) characteristics and did not
include the intermediate-field (boundary interaction and
density current development) or far-field characteristics
(density currents and passive mixing and transport) of the
brine [4].
Modeling the environmental impacts of brine waste
discharges into the sea is a difficult and a complex task.
The difficulties arise from the variety and variability of
the mixing processes that subsequently dilute, spread and
transport the brine plume. Dynamic nature of the marine
environment (currents, waves, and tides), static condi-
tions of disposal site (depth, bottom slope), the configu-
ration of the marine outfall (number of ports, port di-
ameter, inclination and riser height), ambient and brine
waste physical and chemical characteristics are among
factors that should be considered for accurate simulation
of outfall operation. Currently, no flexible and widely
validated predictive tool exists to deal with the special
geometrical aspects of such brine discharges, encom-
passing both the initial negatively buoyant free jets and
the final bottom density current plumes [4].
Given the scarcity of reliable experimental data (nota-
bly dilution measurements) for the entire negatively
buoyant jet, a program of experimental studies supported
by detailed computational fluid dynamics (CFD) model-
ing, appears to be crucial in view of ongoing design and
sitting activities for numerous new desalination plants all
around the globe. The study in hand presents the out-
comes of laboratory experiments of submerged nega-
tively buoyant jet discharging over a flat bottom in a
calm ambient environment to investigate the jet trajec-
tory and dilution. The study is supported by numerical
investigation of the jet dilution and trajectory using the
state of the art Fluent CFD package.
2. Previous Experimental Studies on Outfalls
Characteristics
The prediction of brine jet characteristics relies heavily
upon semi-empirical formulations. These formulas show
that the vertical extent of the jet is dependent upon the jet
velocity, port diameter, and the density ratio between the
ambient and effluent fluids and the dilution of the jet is
dependent on the port velocity and geometric parameters
as well as the ambient current velocity. Table 1 presents
a list of the developed semi-empirical formula from pre-
vious studies.
There are significant variations in the reported results
of the experimental and field studies concerning nega-
tively buoyant jet. Some variations may be attributed to:
the methods adopted in defining and measuring maxi-
mum jet height, the effect of Reynolds number, the effect
of relative density difference, and the effect of mass flux.
Accordingly, the objective of this study is to conduct
experimental and numerical study for the negative dense
jets. The objective of the experimental investigation is to
reproduce a number of lab experiments for the negative
dense jets so as to be sure of all the jet and ambient pa-
rameters then to conduct a numerical analysis for some
selected cases of the lab experiments and to compare the
results
Table 1. Summary of some of the previous studies on dense
jet problem.
No.Ref. Exp./Field Zm
1 Turner, 1966 [15] Exp Zm/r = 2.46Fr
2 Abraham, 1967 [16] Exp Zm/r = 2.74Fr
3 Cederwal, 1968 [17] Exp Zm/r = 4.59(Fr)0.67
4 Fan et al.,1969 [18] Exp Zm/r = 2.68Fr
5 Zeitoun, 1970 [19] Exp Zm/r = 2.43Fr
6 Holly, 1972 [20] Exp Zm = (3.4 × 10–0.148Fe)Fr
7 Chu, 1974 [21] Math Zm = 1.14Lm(Lm/Lb)1/3
8 Tong, 1979 [22] Exp Zm = 1.7Vo(Do/g/)
9 James, 1983 [23] Exp Zm/r = 2.57Fr
10 Mcllelan, 1986 [24] Field Zm/r = 3.11Fr
11 El-Damak, 1990 [25] Exp Zm/r = 3.11Fr6/16
12 Roberts, 1997 [26] Exp Zm/r = 3.11Fr (θ = 60o)
13 Zhang, 1998 [27] Exp Zm/r = 3.06Fr
14 Pantokratoras, 1999 [28]Exp Ym/Do =1.74 Sin (θo)1.53
0
60


0
60



Experimental and Numerical Investigation of Desalination Plant Outfalls in Limited Disposal Areas 830
3. Dimensional Analysis
Consider a miscible jet of dense fluid issuing vertically
from a round source in a homogeneous and calm envi-
ronment. The maximum vertical penetration, Zm of the jet
is dependent on variables that characterize the source
conditions. A general functional relationship for the de-
pendent variable Zm is:

,,
moo

o
Z
fQM B (1)
where:
Qo the jet outlet mass flux = (πr2V);
Mo the momentum flux = (πr2V2),
Bo the buoyancy flux = (πr2VΔρ/ρa),
r the radius of the jet port,
ρa the density of the ambient fluid,
Δρ the density difference between the ambient
fluid and the jet &
V the fluid average velocity at the port’s outlet.
For small distances from the nozzle the volume flux of
the entrained ambient fluid becomes approximately equal
to the initial volume flux so that the initial volume flux
becomes dynamically unimportant and may be ignored
[27]. Thus, it can be deduced from dimensional analysis
that:
34 12
mooo mr
Z
CMBC rF

 (2)
where:
Co & Cm constants that must be determined from
experiments &
Fr the jet densimetric Froude number.
As shown in the previous studies, the maximum pene-
tration for a point source is linearly proportional to Fr.
This fundamental property has been used to analyze & to
determine the constant Cm. The values of densimetric
Froude number can be plotted against the values of the
dimensionless quantity Zm/r for the different sets of ex-
perimental observations.
4. Experimental Investigation
4.1. Experimental Setup
A 1:10 physical model of limited extent and dimensions
was built at the Irrigation and Hydraulics laboratory, Fa-
culty of Engineering, Cairo University. The model re-
produces prototype dimensions of 12.0 m long and 6.0 m
wide with a water depth of 6.0 m. The model scale was
selected such that the penetration of the dense effluent jet
does not exceed the model boundaries.
A stagnant fresh water is used as a fluid ambient (cor-
responds to seawater in the prototype); while salt and dye
are mixed with freshwater in a holding tank to represent
the dense brine and the mix is pumped through the jet
port. Various model ports’ diameters were tested. The
tested model diameters correspond to (5.0, 10.0 & 15.0
cm) diameters in the prototype scale. A wide range of
prototype velocities were tested in the model, the tested
velocity range corresponds to prototype velocities from
0.46 to 4.0 m/sec.
Figure 1 shows the different elements of the labora-
tory setup of the dense jet model experiment. Among
these elements are:
1) Fresh water tank (FWT),
2) Salt water tank (SWT),
3) Auxiliary water tank,
4) Pump and motor,
5) Fitting and valves,
6) Nozzles,
7) Samples extraction mechanism,
8) Temperature conductivity meter,
9) Sensitive scale,
10) Calibrated containers &
11) Dye injection system.
4.2. Experimental Procedure
The dense jet experiment is carried out by discharging
saltwater into a transparent tank filled with fresh water to
produce the required difference in density between the
discharged dense jet and the ambient fresh water. The
amount of salt (NaCl) required to produce the density
difference for a given test is determined by weight and
checked using the temperature conductivity meter. The
temperatures of the fresh water and saltwater were prac-
tically identical and close to room temperature to mini-
mize thermal effects on the flow. During a test, the salt-
water is discharged from SWT to the FWT at a constant
flow rate, which was controlled by keeping constant dif-
ference in head between water levels in FWT and the
Figure 1. A photogr aph of the experimental setup with lim-
ited extent.

Experimental and Numerical Investigation of Desalination Plant Outfalls in Limited Disposal Areas831
SWT using overflows arrangements in both tanks, in
addition to a control valve.
Nine series of model tests were conducted to investi-
gate both small and large densimetric Froude number
jets, while maintaining turbulent flow conditions at the
exit. The nine series of tests cover the following ranges:
three port diameters (5 mm, 10 mm, and 15 mm) with
three different values of salinity that cover a broad range
of conditions (5000 ppm, 10000 ppm, 30000 ppm), Ta-
ble 2.
4.3. Jet Structure
When the discharge valve is suddenly opened at the be-
ginning of the test, the initial development of the jet is
characterized by the formation of a turbulent front that
moved upward and then collapsed. After the collapse of
the starting front, the height of the jet fluctuates with
time, as noted in previous studies. At small densimetric
Froude number the fluctuations are small and the jet pe-
netration is stable. The amplitude of the jet height fluc-
tuation increased with the increase of the densimetric
Froude number. A vertical gauge mounted in the fresh
water tank is used to measure the jet penetration above
the nozzle. The maximum jet penetration, Zm, is deter-
mined as an average of three consecutive maximum jet
heights attained after the collapse of the starting front.
Dye was injected to enhance the visibility in the fresh
water tank. Figure 2 presents two photographs of nega-
tively buoyant jets discharged vertically in calm and ho-
mogenous environment. They are captured during the
test series 4. The densimetric Froude numbers for the jets
in Figure 2 are 28.0 and 33.8 respectively and the aver-
age steady maximum penetration depths are 20 and 23.5
cm respectively.
4.4. Sampling Process of Concentrations along
Dense Jet Trajectory
In order to measure the concentration along the jet, a
number of sampling points extracting from different
heights above the port is constructed. For each test, water
samples along the jet trajectory are extracted using the
samples extraction mechanism for the determination of
Table 2. Summary of tested conditions.
Test Series r (mm)

 Fr
1 2.5 0.00346 28 - 64.5
2 5 0.00346 23 - Dec
3 7.5 0.00353 4.2 - 15.8
4 2.5 0.00736 23.9 - 59.4
5 5 0.00736 11.7 - 31.8
6 7.5 0.0074 4.2 - 16.2
7 2.5 0.0224 17.4 - 56.9
8 5 0.0224 12.3 - 24.5
9 7.5 0.0224 6.5 - 11.1
(a) (b)
Figure 2. Jet Structure of Dense Jets for Port Diameter
5mm. (a) Fr = 33.8 & Zm = 23.5cm; (b) Fr = 28 Zm= 20 cm.
the dilution or salinity profile along the jet trajectory. For
observations in which the maximum jet penetration is
small and below the considered sampling point, only the
first sample close to the nozzle is extracted according to
the maximum jet penetration. The conductivity of the
different samples is determined for each test using the
temperature conductivity probe.
4.5. Jet Velocity at Port End
One of the most important observed parameters in the
dense jet experiment is the jet velocity at port surface.
The volume-time approach is used to determine the dis-
charge through the jet ports. The jet velocities are deter-
mined by dividing the discharge by the cross sectional
area of the nozzle and the average value for jet velocities
are used in further analysis.
5. Results of Laboratory Experimental
Observations
Figure 3 summarizes the results of all the experimental
lab observations as per the conducted 9 test series in this
study (refer to Table 2). The figure presents a relation
between the densimetric Froude number and the normal-
Zm/r = 2.73 Fr
0
50
100
150
200
0 2040608
Zm/r
Densimetric Froude Number0
Z
B
Figure 3. Densimetric froude number versus Zm/r for the
whole sets of experimental obse r vations (c ur rent study).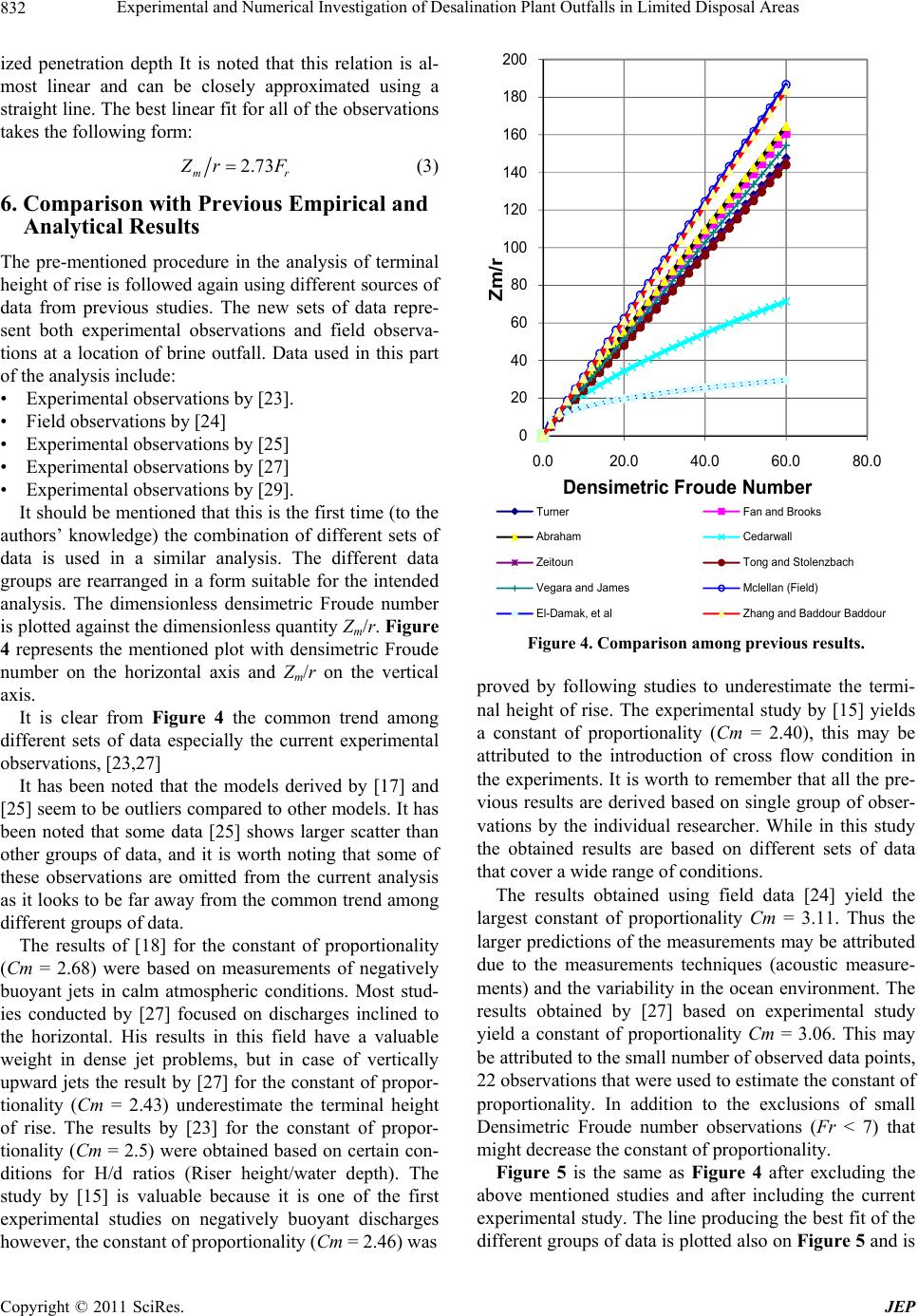

Experimental and Numerical Investigation of Desalination Plant Outfalls in Limited Disposal Areas 832
ized penetration depth It is noted that this relation is al-
most linear and can be closely approximated using a
straight line. The best linear fit for all of the observations
takes the following form:
2.73
mr
Z
rF

(3)
6. Comparison with Previous Empirical and
Analytical Results
The pre-mentioned procedure in the analysis of terminal
height of rise is followed again using different sources of
data from previous studies. The new sets of data repre-
sent both experimental observations and field observa-
tions at a location of brine outfall. Data used in this part
of the analysis include:
• Experimental observations by [23].
• Field observations by [24]
• Experimental observations by [25]
• Experimental observations by [27]
• Experimental observations by [29].
It should be mentioned that this is the first time (to the
authors’ knowledge) the combination of different sets of
data is used in a similar analysis. The different data
groups are rearranged in a form suitable for the intended
analysis. The dimensionless densimetric Froude number
is plotted against the dimensionless quantity Zm/r. Figure
4 represents the mentioned plot with densimetric Froude
number on the horizontal axis and Zm/r on the vertical
axis.
It is clear from Figure 4 the common trend among
different sets of data especially the current experimental
observations, [23,27]
It has been noted that the models derived by [17] and
[25] seem to be outliers compared to other models. It has
been noted that some data [25] shows larger scatter than
other groups of data, and it is worth noting that some of
these observations are omitted from the current analysis
as it looks to be far away from the common trend among
different groups of data.
The results of [18] for the constant of proportionality
(Cm = 2.68) were based on measurements of negatively
buoyant jets in calm atmospheric conditions. Most stud-
ies conducted by [27] focused on discharges inclined to
the horizontal. His results in this field have a valuable
weight in dense jet problems, but in case of vertically
upward jets the result by [27] for the constant of propor-
tionality (Cm = 2.43) underestimate the terminal height
of rise. The results by [23] for the constant of propor-
tionality (Cm = 2.5) were obtained based on certain con-
ditions for H/d ratios (Riser height/water depth). The
study by [15] is valuable because it is one of the first
experimental studies on negatively buoyant discharges
however, the constant of proportionality (Cm = 2.46) was
0
20
40
60
80
100
120
140
160
180
200
0.020.0 40.0 60.0 80.0
Zm/r
Densimetric Froude Number
Turner Fan and Brooks
Abraham Cedarwall
Zeitoun Tong and Stolenzbach
Vegara and JamesMclellan (Field)
El-Damak, et alZhang and Baddour Baddour
Figure 4. Comparison among previous results.
proved by following studies to underestimate the termi-
nal height of rise. The experimental study by [15] yields
a constant of proportionality (Cm = 2.40), this may be
attributed to the introduction of cross flow condition in
the experiments. It is worth to remember that all the pre-
vious results are derived based on single group of obser-
vations by the individual researcher. While in this study
the obtained results are based on different sets of data
that cover a wide range of conditions.
The results obtained using field data [24] yield the
largest constant of proportionality Cm = 3.11. Thus the
larger predictions of the measurements may be attributed
due to the measurements techniques (acoustic measure-
ments) and the variability in the ocean environment. The
results obtained by [27] based on experimental study
yield a constant of proportionality Cm = 3.06. This may
be attributed to the small number of observed data points,
22 observations that were used to estimate the constant of
proportionality. In addition to the exclusions of small
Densimetric Froude number observations (Fr < 7) that
might decrease the constant of proportionality.
Figure 5 is the same as Figure 4 after excluding the
above mentioned studies and after including the current
experimental study. The line producing the best fit of the
different groups of data is plotted also on Figure 5 and is

Experimental and Numerical Investigation of Desalination Plant Outfalls in Limited Disposal Areas833
Figure 5. Terminal height of rise for different groups of
data.
also given in Equation (4) below. The constant,
takes a value of 2.63 and the equation that simulates the
terminal height of rise of negatively buoyant plumes dis-
charged vertically in homogeneous and calm environ-
ment takes the following form:
C
2.63
mr
Z
rF

(4)
The scatter of the data points around the straight line is
expected because of the wide range of covered parame-
ters. It has been noted that the average error between the
predicted values using Equation (3) and Equation (4) is
found to be about 10%. The upper and lower envelopes
based on the different data sets are also plotted on the
figure.
It might be recommended that designer could depend
on Equation (4) which is based on the whole observed
data to represent the maximum jet height of a negatively
buoyant effluent. Equation (4) provides a method of bal-
ancing port diameter, total dense effluent flow, and rela-
tive density difference to obtain a desired maximum jet
height. And can be used for design issues.
7. Numerical Experiments
7.1. The Theoretical Approach of the CFD
Package:
FLUENT [30] is one of the CFD commercial packages
that are commonly used for studying the hydrodynamics
of complicated flow fields including multiphase flow
applications. In the study in-hand, FLUENT package [30]
is adopted for carrying out all numerical simulations.
This problem is considered as one of the most sophisti-
cated problems of fluid dynamics, where it considers a
multi-phase unsteady turbulent flow.
To change from a single-phase model, where a single
set of conservation equations for momentum and conti-
nuity is solved, to a multi-phase model, additional sets of
conservation equations must be introduced. In the proc-
ess of introducing additional sets of conservation equa-
tions, the original set must also be modified.
Since the problem is solved as unsteady flow, the equ-
ation is updated each time step, which is taken 0.2 sec in
this problem. The governing equations are solved se-
quentially for this numerical simulation, because the eq-
uations are nonlinear.
Turbulent flows are characterized by fluctuating ve-
locity fields. These fluctuations mix transported quanti-
ties such as momentum, energy, and species concentra-
tion, and cause the transported quantities to fluctuate as
well. Since these fluctuations in this case study were of
small scale and high frequency, they were too computa-
tionally expensive.
The description of discussed multi-phase flow as in-
terpenetrating continua incorporates the concept of phas-
es volume fractions, denoted here by αq. Volume frac-
tions represent the space occupied by each phase, and the
laws of conservation of mass and momentum are satis-
fied by each phase individually. The derivation of the
conservation equations can be done by ensemble averag-
ing the local instantaneous balance for each of the phases
or by using the mixture theory approach.
The volume of phase q, Vq, is defined by
d
qvq
  VV
q
(5)
where
2
1
1
q
q



 (6)
The effective density of phase q is
ˆqq



 (7)
where
q

The physical density of phase q.
Conservation of Mass
The general form of the conservation of mass equation
for phase q is
 
1
n
qqqqq pq
p
m
t
 

 

 (8)
where
q

The velocity of phase q
p
q
m
 Characterizes the mass transfer from the pth
to qth phase.
From the mass conservation once can obtain
p
q
mm

qp
(9)
0
pp
m
 (10)
The continuity equation for the studied multi-phase
problem, as solved by [23], is presented here for the gen-
eral case of a multi-phase flow. The volume fraction of

Experimental and Numerical Investigation of Desalination Plant Outfalls in Limited Disposal Areas 834
each phase is calculated from a continuity equation:
 
2
1
d
1
d
.qq
qq pqq
p
q
m
tt

 



 






(11)
The solution of this equation for each secondary phase,
along with the condition that the volume fractions sum to
one (given by Equation (8)), allows for the calculations
of the primary-phase volume fraction.
Conservation of Momentum
The general form of the conservation of momentum
equation
 


,,
2
1
lift qvmq
qq qqqq
q
qpq
p
qq q
t
pT m
 







R
FF F



pqpq
(12)
where
q
T is the qth phase stress-strain tensor

2
3
T
qqqqqq qqq
TI  

 




(13)
The conservation of momentum equation for the stud-
ied multi-phase flows, as solved by [30], is presented
here for the general case of a multi-phase flow. The con-
servation of momentum for a fluid q is
 


 
,
,
2
1
vm q
qqq qqqq
q
qq qq qqliftq
pqpqpqpq
p
t
pT
Km
 







gFFF


 
(14)
The conservation of momentum for the fluid phases is
similar to Equation (23), and that for the “s” solid phase is

 
 


,
,
2
1
2
3
vm s
T
qqqqqq qqq
s sss sss
s
sss ss sslifts
lslslsls
l
TI
t
pp T
Km
 
 



 




 


gFFF

 

 
(15)
Euler’s equation was applied to sort out the above eq-
uations.
7.2. The 3D Numerical Model Development and
Boundary Conditions
The case study in-hand is an unsteady multiphase turbu-
lent flow. A three dimensional model was constructed for
this regard using Fluent package. The model boundary
conditions are as follow: the bed side is assumed wall
boundary. The inlet velocity plan is located 5cm above
the bed levels. Due to the model tank symmetry, the
symmetrical option is used in both directions and thus
one fourth the model domain is simulated to minimize
the number of nodes and elements as shown in Figure 6.
The model comprises 94,684 tetrahedral cells and
184,977 triangular interior faces as shown in Figure 7,
which was created by [31].
Two different densities, 1.00346 ρw & 1.00736 ρw are
assumed in this study, where three inlet velocities are
assumed for each density. One inlet diameter (r = 0.05 m,
is assumed in all studied runs, refer to Table 3.
7.3. Results of the Numerical Investigations
Figures 8-13 illustrate the results of the six numerical
Figure 6. The numerical model (one fourth of the domain).
Figure 7. The numerical mesh.

Experimental and Numerical Investigation of Desalination Plant Outfalls in Limited Disposal Areas835
Table 3. List of conducted numerica l experiments.
Numerical Run #
r
(mm) Jet Density Jet Velocity (m/s)
1 5 1.00346ρw 0.2211
2 5 1.00346ρw 0.424
3 5 1.00346ρw 0.8403
4 5 1.00736ρw 0.3144
5 5 1.00736ρw 0.5844
6 5 1.00736ρw 1.1485
Table 4. Comparison of numerical results with semi-em-
pirical formulas.
Penetration Depth (m)
Run # Numerical Equation (4) Min. Envelop* Max. Envelopa
1 0.164 0.1639 0.123 0.192c
2 0.314 0.314 0.236 0.368
3 0.547 0.6226 0.4675 0.7298
4 0.155 0.1597 0.1199 0.1872
5 0.292 0.2969 0.2229 0.348
6 0.513 0.5834 0.4381 0.6839
aFor minimum and maximum envelops, refer to Figure 5.
runs as shown in Table 3 respectively. Four brine con-
centration ratios are shown in each Figure, which are
50%, 20%, 10% & 1%. The maximum penetration height
is assumed to be equal to brine concentration ratio 1%.
The results show that, when the brine is lighter, it reaches
its maximum height quicker before it spreads horizon-
tally as shown in Figures 8-10. Table 4 presents all nu-
merical results. The table also compares the results with
the empirical equations (Equation 4) and the upper and
lower envelops identified in Figure 5. Figure 14 illus-
trate the velocity vectors for one of the numerical runs. It
is worth to be noted that all the numerical results are
bounded by the upper and lower envelops identified in
Figure 5.
7.4. The Brine Breakthrough Curves
(Concentration with Time)
One of the advantages of using numerical simulation is
developing the relation between the brine concentration
ratio and the time. Figures 15 and 16 represent the tem-
poral variation of the brine concentration with the course
of time for an example run (run No.5) where the maxi-
mum penetration height is 29.2 cm. The brine concentra-
tion breakthrough curve is given every 2 cm. Figure 15
represents the breakthrough curves for vertical heights
from 2 cm to 14 cm measured from the port, whereas
Figure 16 gives the corresponding brine breakthrough
curves for heights from 16 cm to 28 cm.
Examination of the simulated breakthrough curves
shows a number of interesting issues that can be summa-
rized as follow: It has been noted that the peak concen-
tration values of the breakthrough curves decrease with
the depth and these peak values start to decrease with the
course of time due to the continuous water entrainment
Figure 8. (penetration height = 0.164 m, Run No. 1) v =
0.2211 m/s, d = 0.1 & density = 1.00346 ρw.
Figure 9. (penetration height = 0.314 m, Run No. 2), v =
0.424 m/s, d = 0.1 m & density = 1.00346 ρw.
Figure 10. (penetration height = 0.547 m, Run No. 3), v =
0.8403 m/s, d = 0.1 m & density =1.00346 ρw.
Figure 11. (penetration height = 0.155 m, Run No. 4), v =
0.3144 m/s, d = 0.1 m & density 1.00736 ρw –.
Figure 12. (penetration height = 0.292 m, Run No. 5), v =
0.5834 m/s, d = 0.1 m & density = 1.00736 ρw –.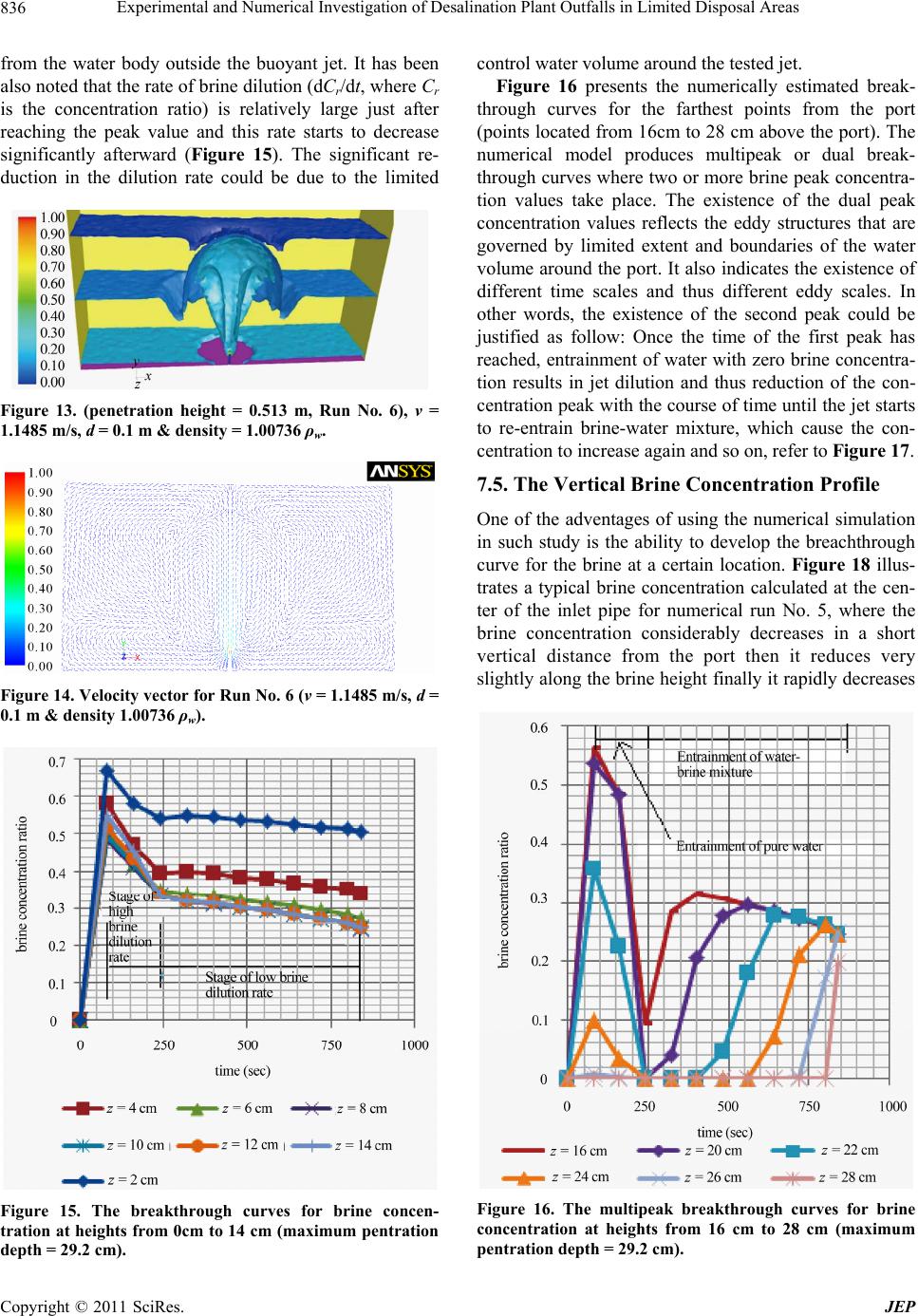

Experimental and Numerical Investigation of Desalination Plant Outfalls in Limited Disposal Areas 836
from the water body outside the buoyant jet. It has been
also noted that the rate of brine dilution (dCr/dt, where Cr
is the concentration ratio) is relatively large just after
reaching the peak value and this rate starts to decrease
significantly afterward (Figure 15). The significant re-
duction in the dilution rate could be due to the limited
Figure 13. (penetration height = 0.513 m, Run No. 6), v =
1.1485 m/s, d = 0.1 m & density = 1.00736 ρw.
Figure 14. Velocity vector for Run No. 6 (v = 1.1485 m/s, d =
0.1 m & density 1.00736 ρw).
Figure 15. The breakthrough curves for brine concen-
tration at heights from 0cm to 14 cm (maximum pentration
depth = 29.2 cm).
control water volume around the tested jet.
Figure 16 presents the numerically estimated break-
through curves for the farthest points from the port
(points located from 16cm to 28 cm above the port). The
numerical model produces multipeak or dual break-
through curves where two or more brine peak concentra-
tion values take place. The existence of the dual peak
concentration values reflects the eddy structures that are
governed by limited extent and boundaries of the water
volume around the port. It also indicates the existence of
different time scales and thus different eddy scales. In
other words, the existence of the second peak could be
justified as follow: Once the time of the first peak has
reached, entrainment of water with zero brine concentra-
tion results in jet dilution and thus reduction of the con-
centration peak with the course of time until the jet starts
to re-entrain brine-water mixture, which cause the con-
centration to increase again and so on, refer to Figure 17.
7.5. The Vertical Brine Concentration Profile
One of the adventages of using the numerical simulation
in such study is the ability to develop the breachthrough
curve for the brine at a certain location. Figure 18 illus-
trates a typical brine concentration calculated at the cen-
ter of the inlet pipe for numerical run No. 5, where the
brine concentration considerably decreases in a short
vertical distance from the port then it reduces very
slightly along the brine height finally it rapidly decreases
Figure 16. The multipeak breakthrough curves for brine
concentration at heights from 16 cm to 28 cm (maximum
pentration depth = 29.2 cm).

Experimental and Numerical Investigation of Desalination Plant Outfalls in Limited Disposal Areas837
Figure 17. Schematic presentation of re-entrainment pro-
cess.
Figure 18. The vertical concentration profile (penetration
height = 0.292 m, Numerical Run No. 5), v = 0.5834 m/s, d =
0.1 m & density = 1.00736 ρw.
till it vanishes.
8. Conclusions
This study concerns the experimental as well as numeri-
cal investigation of the buoyant dense jet that comes out
from the disposal of the brine water via the desalination
plants’ outfalls. The work in this paper is divided into
two stages. In the first stage, experimental investigation
has been conducted, based on that a new empirical for-
mula describing the penetration depth (the terminal
height of rise) of dense jets is presented. The analysis of
the measurements from current experiments and data
from previous works confirm the validity of the linear
penetration depth function in terms of the densimetric
Froude number. Upper and lower envelops have been
also identified for this linear formula.
In the second stage, a number of 3D numerical runs,
using Fluent CFD package, has been conducted for simi-
lar conditions. Comparison of the numerical results and
the empirical trends shows that the numerical model re-
sults generally agree well with the empirical investiga-
tions. The numerical simulation has revealed the exis-
tence of multipeak or dual breakthrough curves for the
brine concentration. Having multipeaks of brine concen-
tration is explained due to the limited extent of the water
volume around each port.
9. Acknowledgements
The authors would like to thank Dar Al-Handasah, “Shair
and partners”, Resource & Environment Department, for
their great and continuous support.
REFERENCES
[1] S. Matthews, “Desalination in Middle East Set to Grow,”
Home/Utilities Middle East, 5 April 2009.
[2] A. Purnama and H. H. Al-Barwani, “Spreading of Brine
Waste Discharges into the Gulf of Oman,” Desalination,
Vol. 195, No. 1-3, 2006, pp. 26-31.
doi:10.1016/j.desal.2005.09.036
[3] Chevron, “Reverse Osmosis Brine Disposal via Ocean
Outfall Environmental Management and Monitoring
Plan,” G1-NT-REPX0001483, Chevron Australia Pty Ltd,
2010, p. 101.
[4] T. Bleninger and G. H. Jirka, “Modelling and Environ-
mentally Sound Management of Brine Discharges from
Desalination Plants,” Desalination, Vol. 221, No. 1-3,
2008, pp. 585-597. doi:10.1016/j.desal.2007.02.059
[5] I. Alameddine and M. El-Fadel, “Brine Discharge from
Desalination Plants: A Modeling Approach to an Opti-
mized Outfall Design,” Desalination, Vol. 214, No. 1-3,
2007, pp. 241-260. doi:10.1016/j.desal.2006.02.103
[6] P. J. W. Roberts and G. Toms, “Inclined Dense Jets in
Flowing Current,” Journal of Hydraulic Engineering, Vol.
113, No. 3, 1987, 232-341.
doi:10.1061/(ASCE)0733-9429(1987)113:3(323)
[7] S. Latteman and T. Höpner, “Seawater Desalination: Im-
pacts of Brine and Chemical Discharge on the Marine
Environment,” Balaban Desalination Publications, Italy,
2003.
[8] R. Einav, K. Harussi and D. Perry, “The Footprint of the
Desalination Processes on the Environment,” Desalina-
tion, Vol. 152, 2002, pp. 141-154.
doi:10.1016/S0011-9164(02)01057-3
[9] T. N. Green, A. G. I. Dalvi and M. A. Javeed, “Chloro-
phyll and Plankton of the Gulf Coastal Waters of Saudi
Arabia Bordering a Desalination Plant,” Desalination,
Vol. 154, No. 3, 2003, pp. 291-302.
doi:10.1016/S0011-9164(03)80044-9
[10] H. Zhang and R. H. Baddour, “Maximum Penetration of
Vertical Round Dense Jets at Small and Large Densimet-
ric Froude Numbers,” Journal of Hydraulic Engineering,
ASCE, Vol. 124, No. 5, 1998, pp. 550-553.
[11] A. Purnama, H. H. Al-Barwani, and M. Al-Lawatia,
“Modeling Dispersion of Brine Waste Discharges from a
Coastal Desalination Plant,” Desalination, Vol. 155, No.
1, 2003, pp. 41-47. doi:10.1016/S0011-9164(03)00237-6
[12] S. Shahatto, “Environmental Impact of Development in
Coastal Areas: Desalination,” Ph.D. Thesis, Centre for
Applied Geosciences, University of Tübingen, Germany,
2003.
[13] P. J. W. Roberts and R. Sternau, “Mixing Zone Analysis
for Coastal Wastewater Discharge,” ASCE Journal of En-

Experimental and Numerical Investigation of Desalination Plant Outfalls in Limited Disposal Areas 838
vironmental Engineering, Vol. 123, No. 12, 1997, pp.
1244-1250.
[14] A. Cipollina, A. Brucato, F. Grisafi and S. Nicosia,
“Bench Scale Investigation of Inclined Dense Jets,” ASCE
Journal of Hydraulic Engineering, Vol. 131, 2005, pp.
1017-1022.
doi:10.1061/(ASCE)0733-9429(2005)131:11(1017)
[15] J. S. Turner, “Jets and Plumes with Negative or Reversing
Buoyancy,” Journal of Fluid Mechanics, Vol. 26, 1966,
pp. 779-792.
[16] G. Abraham, “Jets with Negative Buoyancy in Homoge-
neous Fluids,” Journal of Hydraulic Research, Vol. 5, No.
4, 1967, pp. 235-248.
[17] K. Cederwall, “Hydraulics of Marine Wastewater Dis-
posal,” hydraulic Division, Chalmers Institute of Tech-
nology, Gutenberg, Sweden, Report No .42, 1968.
[18] L. N. Fan and N. H. Brooks, “Numerical Solutions of
Turbulent Buoyant Jet Problems,” Report No. KH-R-18,
California Institute of Technology, W. M. Keck Labora-
tory, Pasadena, California, 1969.
[19] M. A. Zeitoun, W. F. Mcllhenny and R. O. Reid, “Con-
ceptual Designs of Outfall Systems for Desalination
Plants,” Report No. 550, Office of Saline Water, US De-
partment of Interior, Washington DC, 1970.
[20] F. M. Holly and A. M. Jr., “Model Study of Dense Jets in
Flowing Fluid,” ASCE Journal of Hydraulic Division,
Vol. 98, No. 11, 1972, pp. 1921-1933.
[21] V. H. Chu and M. B. Goldberg, “Buoyant Forced Plumes
in a Cross Flow,” ASCE Journal of Hydraulic Division,
Vol. 100, No. 9, 1974, pp. 1203-1214.
[22] S. S. Tong and K. D. Stolzenbach, “Submerged Discharge
of a Dense Effluent,” Report No. 243, Ralph M Parsons
laboratory, Massachusetts Institute of Technology, Cam-
bridge, 1979.
[23] W. P. James, I. Vegara and K. Kim, “Dilution of a Dense
Vertical Jet,” ASCE Journal of Environmental Engineer-
ing, Vol. 109, No. 6, 1983, pp. 1273-1283.
[24] T. N. Mcllelan and R. E. Randall, “Measurement of Brine
Jet Height and Dilution,” ASCE Journal of Waterway,
Port, Coastal and Ocean Engineering, Vol. 112, No. 2,
1986, pp. 199-204.
[25] R. M. El-Damak, M. F. Helwa and Y. R. Marmoush,
“Release of Heavy Wastewater into Aquatic Environment,
Experimental Investigation,” Journal of Engineering, Fa-
culty of Engineering, Cairo University, 1990.
[26] P. J. W. Roberts and G. Toms, “Inclined Dense Jets in
Flowing Current,” Journal of Hydraulic Engineering, Vol.
113, No. 3, 1987, 232-341.
doi:10.1061/(ASCE)0733-9429(1987)113:3(323)
[27] H. Zhang and R. H. Baddour, “Maximum Penetration of
Vertical Round Dense Jets at Small and Large Densimet-
ric Froude Numbers,” ASCE Journal of Hydraulic Engi-
neering, Vol. 124, No. 5, 1998, pp. 550-553.
[28] A. Pantokratoras, “Vertical Penetration of Heated Water
Jets Discharged Downwards,” ASCE Journal of Envi-
ronmental Engineering, Vol. 125, No. 4, 1999, pp. 389-
392.
[29] M. E. Abou-El-Haggag, “Environmental Assessment of
Brine Disposal via Marine Outfalls,” Master Thesis, Fac-
ulty of Engineering, Cairo University, 2005.
[30] Fluent Manual for the ANSYS Release 12.1.4, ANSYS
Inc., 2009.
[31] “Gambit 2.3 User’s guide,” Ansys Release, ANSYS Inc.,
2006.

Experimental and Numerical Investigation of Desalination Plant Outfalls in Limited Disposal Areas839
Notations
o
C The brine concentration at any height from the
port
B The buoyancy flux,
Co The experimental constant,
Cm The experimental constant,
Cp The brine concentration at the port.
Cr The concentration ratio = C/Cp
f
The drag function,
,qlift
F Lift force,
q
F
External body force,
Fr The jet densimetric Froude number,
,vm q
F Virtual mass force,
g
The acceleration due to gravity,
Mo The momentum flux,
p
q
m

p
The mass transfer from the pth to qth phase,
The pressure shared by all phases,
s
p The sth solids pressure,
q The phase,
Qo The jet outlet mass flux,
r The radius of the jet port,
q
R Interaction force between phases,
p
T The particulate relaxation time,
q
T The qth phase stress-strain tensor,
V The fluid average velocity,
q
V The volume of phase q,
m
Z
The maximum vertical penetration,
q

q
th fluid’s volume fraction in the cell,
q

The velocity of phase q,
p
q

The interphase velocity,
q

Bulk viscosity of phase q,
q

Shear viscosity of phase q,
q

The physical density of phase q,
ˆq

The effective density of phase q.

a The density of the ambient fluid &
 The density difference between the ambient
fluid and the jet.