 J. Biomedical Science and Engineering, 2009, 2, 323-335 doi: 10.4236/jbise.2009.25048 Published Online September 2009 (http://www.SciRP.org/journal/jbise/ JBiSE ). Published Online September 2009 in SciRes. http://www.scirp.org/journal/jbise CANFIS—a computer aided diagnostic tool for cancer detection Latha Parthiban1, R. Subramanian2 1Research Scholar in Pondicherry University and working in Aarupadai Veedu Institute of Technology, Chennai, India; 2Department of Computer Science, Pondicherry University, Puducherry, India. Email: 1lathaparthiban@yahoo.com, 2subbur@yahoo.com Received 5 November 2008; revised 20 May 2009; accepted 25 May 2009. ABSTRACT In this investigation, an approach using Coac- tive Neuro-Fuzzy Inference System (CANFIS) as diagnosis system for breast cancer has been proposed on Wisconsin Breast Cancer Data (WBCD). It is occasionally difficult to attain the ultimate diagnosis even for medical experts due to the complexity and non-linearity of the rela- tionships between the large measured factors, which can be possibly resolved with a human like decision-making process using Artificial Intelligence (AI) algorithms. CANFIS is an AI algorithm which has the advantages of both fuzzy inference system and neural networks and can deal with ambiguous data and learn from the past data by itself. The Multi Layer Percep- tron Neural Network (MLPNN), Probabilistic Neural Network (PNN) Principal Component Analysis (PCA), Support Vector Machine (SVM) and Self Organizing Map (SOM) were also tested and benchmarked for their performance on the classification of the WBCD. Keywords: Neural Network; Coactive Neuro-Fuzzy Inference Systems; Probabilistic Neural Network; Principal Component Analysis; Stern Series; Wis- consin Breast Cancer Data 1. INTRODUCTION Breast cancer is the most common tumor-related disease among women throughout the world, and the mortality rate caused by breast cancer is dramatically increasing. The etiologies of breast cancer remain unclear and no single dominant cause has emerged [1]. Preventive way is still a mystery and the only way to help patients to survive is by early detection. If the cancerous cells are detected before spreading to other organs, the survival rate for patient is more than 97% [25] which is the mo- tivation factor to develop this automated diagnostic tool. Again, a major class of problems in medical science in- volves the diagnosis of disease, based upon several tests performed upon the patient and this has given rise, over the past few decades, to computerized diagnostic tools, intended to aid the physician in making sense out of the confusing data [2]. There have been substantial previous research works with WBCD database to achieve an automatic ultimate diagnostic system. Genetic Algorithm (GA) [2,13], Fuzzy Inference Systems(FIS) [3,4], Neural Networks (NN) [5,12], Adaptive Boosting (AdaBoost) [6,10,11] and Neuro-Fuzzy Hybrid Models [4,8] have been ap- plied to this problem. The performances of each infer- ence system were evaluated by calculating the degree of correctness in predicted results against diagnosed results represented as PPV (Positive Predicted Value). Each system shows the PPV within the range from less than 60% (AdaBoost) up to over 95% (Neuro-Fuzzy Hybrid Models). Among those algorithms, Neuro-Fuzzy Hybrid models provide relatively remarkable performances in diagnosis. Those models are the combination of Neural Networks and Fuzzy Inference Systems encouraging the advantages and resolving the drawbacks of both NNs and FIS models. For our experiments, after preprocessing and cleaning of clinical data from mammogram, a modified method of using CANFIS [8,9] was applied to attain the ultimate diagnosis as being either benign or malignant. In order to find the neural network model with the highest accu- racy for classification of the WBCD, we implemented five types of classifiers: Multi Layer Perceptron Neural Network (MLPNN), Probabilistic Neural Network (PNN), Principal Component Analysis (PCA), Support Vector Machine (SVM) and Self Organizing Map (SOM). To achieve fast training, the weights of these classifiers were initialized with Stern series. In applying CANFIS and other artificial intelligent algorithm, the required system size is changed in proportion to the size  324 L. Parthiban et al. / J. Biomedical Science and Engineering 2 (2009) 323-335 SciRes Copyright © 2009 JBiSE of the inference system such as the number of inputs, the number of internal nodes and the number of learning iteration. Among those critical factors of the inference system, the number of internal nodes and learning itera- tion are changeable only in the process of designing the system. Therefore, methods for reducing the number of input factors within range of not losing the accuracy of diagnosis were considered. For this purpose, we used two methods, which are decision tree [14] and the corre- lation coefficient between the individual inputs and the test diagnosis results. The overall process flow chart is presented in Figure 1. The rest of this paper is organized as follows: In Section 2, we briefly describe the WBCD data, data cleaning and feature extraction, dominant input selec- tion methods, a review of the classifiers that are con- sidered and initializing the weight of neural networks with Stern series are presented. In Section 3, we pre- sent the diagnostic system using CANFIS. In Section 4, experimental results of the classifiers trained on com- posite features of the WBCD data is compared in terms of positive predicted value and discussion of the pre- sented results is provided in the light of existing stud- ies in the literature. In Section 5, we highlight the re- sults of the paper and finally, in Section 6, we con- clude the paper. 2. METHODS 2.1. Wisconsin Breast Cancer Database The Wisconsin Breast Cancer Diagnosis (WBCD) data- base is the result of efforts provided by the University of Wisconsin Hospital based on microscopic examination of breast masses with fine needle aspirate tests. Fine needle aspiration of breast masses is a common non- invasive diagnostic test that obtains information needed to evaluate malignancy [3,15]. Figure 1. Overall processes flowchart. Masses often characterize as early breast cancer be- fore it is palpable by a woman or a physician [1]. It has its own characteristics and may be used as a clue to clas- sify them. Masses can be circumscribed, speculated (sat- ellite), lobulated or ill-defined (irregular) and radiologist will need to take a good look at its texture information, statistical descriptions as well as the background tissue from mammography images. Therefore, in order to clas- sify a mass, the characteristics or attributes recorded were used as an input features. There are nine criteria recorded for masses in this dataset represented as a 1-10 integer value. (Table 1). The database (Table 2) itself contains 699 cases, with 65.5% classified as benign and 34.5% as malignant. The diagnostics do not provide any information about the degree of benignity or malignancy. In considering the relationship between the measured values and the diag- nostics, there are almost no relationships which stand out. Therefore, there is no convenient and effective method to attain the ultimate diagnostics with this original data even for the specialists. In addition to that, there may be the possibility that one or more of the measured pieces do not affect the diagnosis result. These are the reasons that artificial in- telligent system can be used as an expert to assist the specialist in diagnosing the disease correctly. 2.2. Data Cleaning and Feature Extraction Preliminary examination on dataset chosen is compul- sory before cleaning process takes place. By knowing the relationship between attributes, and how strongly they depend on each other, data quality and evaluation can be found easily. The discovery of data relationship Table 1. Dataset features. Criteria Integer Value Clump Thickness X1 Uniformity of Cell Size X2 Uniformity of Cell Shape X3 Marginal Adhesion X4 Single Epithelial Cell Size X5 Bare Nuclei X6 Bland Chromatin X7 Normal Nucleoli X8 Mitosis X9 Clinical data from Mammogram Preprocess data Table 2. WBCD database. Case X1X2X3……... X9 Diagnostics 1 5 1 1 …….. 1 Benign 2 5 4 4 …….. 1 Benign … .. .. .. …….. .. … … .. .. .. …….. .. … 6994 8 8 …….. 1 Malignant Selected attributes Cleaned data All attributes Neural Network model for data mining Dominant input selection methods Classification Result  L. Parthiban et al. / J. Biomedical Science and Engineering 2 (2009) 323-335 325 SciRes Copyright © 2009 might lead to data cleaning rules, and therefore it can suggest improvements to its constraints. These are car- ried out by analyzing patterns between the attributes, using statistical tools like bivariate or multivariate analysis. Therefore, two different cleaning processes have been carried out on the dataset. Dataset named Set A will only eliminate records with missing value and outliers, with the hypothesis that medical data are best not to be tam- pered or changed. While data in Set B will undergo normal statistical cleaning process where all attributes must be distributed normally. Therefore, data in Set B has been changed many times to fulfill the normal dis- tribution functions JBiSE Using Neural Connection 2.0, 180 simulations was carried out for both dataset to test which data set is the best. As shown in Figure 2, set A gives 100% as the highest accuracy percentage (AP) and the smallest root mean squared (RMS) error is only 0.02751. As com- pared to set B, the highest AP is only 83.36% with smallest RMS error is 0.21002. It is proven that our hy- pothesis is true and therefore, set A will be used as an input database. After data cleaning, the data in the WBCD database was divided into two sets: training and testing datasets. There are 444 benign and 238 malignant cases in the database. The training dataset constitutes 50% of WBCD database taken in order and the remaining is testing dataset. The training dataset was also used to figure out the most effective and dominant inputs of the inference system and the result with dominant inputs using deci- sion tree and correlation coefficient computation was tested for correctness verification of the output. 2.3. Dominant Input Selection Methods 2.3.1. Decision Tree The input recommender used in our experiment was a decision tree learning algorithm using SAS9™ package. The decision tree construction algorithms generate deci- sion trees from a set D of cases. These algorithms parti- tion the data set D into subsets D1, D2, ……DM by a set of tests X with mutually outcomes X1, X2 ,……. XM, where Dv contains those cases that have outcome Xi. A decision tree (DT) is known as a good classifier of huge data. It classifies input data by partitioning example spaces with entropy calculation. DT is especially useful when dataset is represented by attribute-value pairs and the target function has discrete output value. In our ex- periment, a binary decision tree was constructed to select dominant inputs. In each node of the tree, the most use- ful attribute for classifying whole data is selected by calculating the information gain (measure for deciding the relevance of an attribute) G (D, X) of an attribute X, Figure 2. Simulations results of data Set A and Set B.  326 L. Parthiban et al. / J. Biomedical Science and Engineering 2 (2009) 323-335 SciRes Copyright © 2009 JBiSE Figure 3. DT dominant input selection. relative to a collection of examples X, with following formula. )()(),( )( DvEntropy D Dv DEntropyXDGain XValuesv and i c i ippDEntropylog)( 1 where pi denotes the proportion of classes in D that belong to the ith class, Va l u e s ( X ) is the set of all possible values for attribute X, Dv is a subset of D for which attribute X has a value v and. |Dv| represents cardinality of Dv dataset. (i.e., D={d D | X(d) = v}). The first term in the equation for Gain is just the entropy of the original collection D and the second term is the expected value of the entropy after D is partitioned using attribute X. The expected entropy described by this second term is simply the sum of the entropies of each subset Dv, weighted by the fraction of examples |Dv|/|D| that belong to Dv. Gain (D,X) is therefore the expected reduction in entropy caused by knowing the value of attribute X. Alternatively, Gain(D,X) is the information provided about the target attribute value, given the value of some other attribute X. The DT is constructed in a way to reduce the entropy with the attribute which has the highest gain value at each node. Through this way, the final DT model has the most useful measured data on the top node, next useful one on the right node of the top node and so on. The input selection process derived by DT is presented in Figure 3. 2.3.2. Correlation Coefficient Computation An efficient method for dominant input selecting process is calculating correlation coefficients between each measured input data and the diagnosis results. The Cor- relation Coefficient is a numerical measure of the degree of the linear relationship between two variables. The value of the correlation coefficient always falls between –1 and 1. A positive correlation coefficient indicates a direct relationship, and a negative correlation coefficient indicates an inverse relationship between two variables. In the calculation, first it is possible to assume that all the correlation coefficients by calculating with data in WBCD should be positive. Then we selected four meas- ured input data from the one which has the highest cor- relation coefficient for diagnosis system. The correlation coefficient indicates the degree of linear relationship between two variables. The correlation coefficient al- ways lies between -1 and +1. -1 indicates perfect linear negative relationship between two variables, +1 indi- cates perfect positive linear relationship and 0 indicates lack of any linear relationship The correlation coeffi- cient(ρij ) can be calculated by the following formula. )()( )(cov , ji ji jjii ij ij XX XX CC C (1) )()( )(,)( 22 XXXXC XXCXXC jiij jjjiii (2) where Cij is the covariance of Xi and Xj, is the mean and σ(Xi) is the standard deviation of Xi and σ(Xj) is the standard deviation of Xj . Each result by the correlation coefficient calculation between each measured input and the correct output indicates the degree of linear relationship between them. In this procedure, the selected input features are possibly said to have more linear relationships so that they affects the results. Therefore, the inputs highly correlated with the output were selected as dominant inputs in our experiment. The result of dominant input selection by the correlation coefficient calculation is given in Figure 4.  L. Parthiban et al. / J. Biomedical Science and Engineering 2 (2009) 323-335 327 SciRes Copyright © 2009 JBiSE Figure 4. Correlation coefficient output. 2.4. Brief Review of Different Classifiers 1) Multilayer Perceptron Neural Network The MLPNNs are the most commonly used neural- network architectures since they have features such as the ability to learn and generalize smaller training-set requirements, fast operation, and ease of implementation. One major property of these networks is their ability to find nonlinear surfaces separating the underlying pat- terns, which is generally considered as an improvement on conventional methods. The MLPNN is a nonparamet- ric technique for performing a wide variety of detection and estimation tasks [12,17,18,19]. Figure 5 shows the architecture of MLPNN. There is one neuron in the input layer for each predictor variable. In the case of categori- cal variables, N-1 neurons are used to represent the N categories of the variable. Input Layer—A vector of predictor variable values (x1...xp) is presented to the input layer. The input layer (or processing before the input layer) standardizes these values so that the range of each variable is -1 to 1. The input layer distributes the values to each of the neurons in the hidden layer. In addition to the predictor variables, there is a constant input of 1.0, called the bias that is fed to each of the hidden layers; the bias is multiplied by a weight and added to the sum going into the neuron. Hidden Layer—Arriving at a neuron in the hidden layer, the value from each input neuron is multiplied by a weight (wji), and the resulting weighted values are added together producing a combined value uj. The weighted sum (uj) is fed into a transfer function, σ, which outputs a value hj. The outputs from the hidden layer are distributed to the output layer. Output Layer-Arriving at a neuron in the output layer, the value from each hidden layer neuron is multiplied by a weight (wkj), and the resulting weighted values are added together producing a combined value vj. The weighted sum (vj) is fed into a transfer function, σ, which outputs a value yk. The y values are the outputs of the network. The algorithm for the MLPNN is given below. It re- quires the units to have thresholding non linear functions that are continuously differentiable, i.e., smooth every- where. A sigmoid function f (net)=1/(1+e-knet), is used, since it has a simple derivative. All training and testing data were normalized. Initialize weights and thresholds: Set all weights and thresholds to small random vari- able. Present input and desired output: Present input: XP = x1, x2,…………… xp Target output: YP = y1,………… ym where, p is the number of input nodes and m is the num- ber of output nodes. Set w0 to be -θ, the bias, and x1 to be always 1. For pattern association, XP and YP represent the pat- terns to be associated. For classification, YP is set to zero except for one element set to 1 that corresponds to the class the XP is in. Calculation of actual output: Each layer calculates and passes it as input to the next layer. The final layer outputs values Op j and passes that as input to the next layer. 1 0 , n i xipi i wfY Adapt weights (start from control layer, and work backwards): wi j(t + 1) = wi j(t) + η δpjOp j where, wi j (t) represents the weights from node i to node j at time t, η is a gain term, and δp j is an error term for pattern p on node j. For output units: δ p j = k Op j (1 -Op j) (tp j -Op j) For hidden units: δp j = kOp j (1 -Op j)∑ δ Pk wjk where, the sum is over the k nodes in the layer above node j. The stopping condition may be weight change, number of epochs, and so on. The main issues involved in designing and training a MLPNN are selecting how many hidden layers to use in the network, deciding how many neurons to use in each hidden layer, finding a globally optimal solution that avoids local minima, converging to an optimal solution in a reasonable period of time and validating the neural network to test for overfitting. 2) Probabilistic Neural Network The PNN introduced by Specht [20] is essentially based on the well-known Bayesian classifier technique commonly used in many classical pattern-recognition problems. Consider a pattern vector with m dimen- sions that belongs to one of two categories K1 and K2. Let F1(x) and F2(x) be the probability density functions (pdf) for the classification categories K1 and K2, respect  328 L. Parthiban et al. / J. Biomedical Science and Engineering 2 (2009) 323-335 SciRes Copyright © 2009 JBiSE Figure 5. Architecture of MLPNN. Figure 6. Architecture of PNN. tively. From Bayes’ discriminant decision rule, be- longs to K1 if 1 2 2 1 2 1 )( )( P P L L xF xF (3) Conversely, belongs to K2 if 1 2 2 1 2 1 )( )( P P L L xF xF (4) where L1 is the loss or cost function associated with misclassifying the vector as belonging to category K1 while it belongs to category K2, L2 is the loss function associated with misclassifying the vector as belonging to category K2 while it belongs to category K1, P1 is the prior probability of occurrence of category K1, and P2 is the prior probability of occurrence of category K2. In many situations, the loss functions and the prior prob- abilities can be considered equal. Hence the key to using the decision rules given by Eq.3 and 4 is to estimate the probability density functions from the training patterns. The PNN architecture (Figure 6) is composed of many interconnected processing units or neurons organ- ized in successive layers. The input layer unit does not perform any computation and simply distributes the in- put to the neurons in the pattern layer. On receiving a pattern from the input layer, the neuron xij of the pattern layer computes its output using  L. Parthiban et al. / J. Biomedical Science and Engineering 2 (2009) 323-335 329 SciRes Copyright © 2009 JBiSE /2 2 ()() 1 () (2 )2 T ij ij ij dd xx xx x exp (5) where d denotes the dimension of the pattern vector x, σ is the smoothing parameter, and xij is the neuron vector [20,21]. For two class problem, if input units is assumed to be x1 to xn, Pattern units be Class A (ZA1 to ZAj) and Class B (ZB1 to ZBj), Summation units be fA and fB and output unit y, then the training algorithm for the probabilistic neural net is Step 1: For each training input pattern, x(p), p=1,……P perform Steps 2-3. Step 2: Create pattern unit Zp: Weight vector for unit Zp: wp=x(p) (unit Zp is either a ZA unit or ZB unit) Step 3: Connect the pattern unit to summation unit. If x(p) belongs to Class A, connect pattern unit Zp to summation unit SA. Else, connect pattern unit Zp to summation unit SB. The application algorithm for classifying is given as Step 1: Initialize weights from training algorithm. Step 2: For input pattern to be classified, do Steps 3–5. Step 3: Patterns units: Calculate net input, Zinj = x.wj=xTwj Calculate the output Z=exp[[Zinj-1]/σ2] Step 4: Summation units The weights used by the summation unit for Class B is, VB=-PBCBmA/PACAmB Step 5: Output unit: It sums the signals from fA and fB. Input vector is classi- fied as Class A if the total input to decision unit is positive. The main advantage of PNN compared to MLPNN is faster to train a PNN network than a MLPNN. more accurate than MLPNN. insensitive to outliers (wild points). generate accurate predicted target probability scores. approach Bayes optimal classification. slower than MLPNN at classifying new cases. require more memory space to store the model 3) Support Vector Machine The SVM proposed by Vapnik [22] has been studied extensively for classification, regression, and density estimation. The SVM is a binary classifier and it maps the input patterns into a higher dimensional feature space through some nonlinear mapping chosen a priori. A lin- ear decision surface is then constructed in this high-di- mensional-feature space. Thus, SVM is a linear classifier in the parameter space, but it becomes a nonlinear clas- sifier as a result of the nonlinear mapping of the space of the input patterns into the high-dimensional feature space. Training the SVM is a quadratic-optimization problem. SVM has been shown to provide high- gener- alization ability. A proper kernel function for a certain problem is dependent on the specific data and till now there is no good method on how to choose a kernel func- tion [22,23]. In this paper, the choice of the kernel func- tions was studied empirically and optimal results were achieved using radial-basis function (RBF) kernel function. SVMs are free of optimization headaches of neural networks because they present a convex programming problem, and guarantee finding a global solution. They are much faster to evaluate than density estimators, be- cause they make use of only relevant data points, rather than looping over each point regardless of its relevance to the decision boundary. 4) Self Organizing Maps Self-organizing maps learn to classify input vectors according to how they are grouped in the input space. Feature maps allocate more neurons to recognize parts of the input space where many input vectors occur and al- locate fewer neurons to parts of the input space where few input vectors occur. SOM also learn the topology of their input vectors. Neurons next to each other in the network learn to respond to similar vectors. The layer of neurons can be imagined to be a rubber net that is stretched over the regions in the input space where input vectors occur. SOM allow neurons that are neighbors to the winning neuron to output values. Thus the transition of output vectors is much smoother than that obtained with competitive layers, where only one neuron has an output at a time. Initially, the weight and learning rate are set. The in- put vectors to be clustered are presented to the network. Once the input vectors are given, based on initial weights, the winner unit is calculated either by Euclid- ean distance method or sum of products method. An epoch is said to be completed once all the input vectors are presented to the network. By updating the learning rate, several epochs of training may be performed. The training algorithm for SOM is as below Step 1: Set topological neighborhood parameters Set learning rate, initialize weights. Step 2: While stopping condition is false do Steps 3-9 Step 3: For each input vector x, do Steps 4-6. Step 4: For each j, compute squared Euclidean distance. D(j)=∑(Wij-Xi)2 i =1 to n and j = 1 to m Step 5: Find index J, when D(j) is minimum. Step 6: For all units J with the specified neighbourhood of J, for all i, update the weights. Wij(new) = Wij(old) + α[xi-Wij(old)] Step 7: Update the learning rate. Step 8: Reduce the radius of topological neighborhood at specified times. Step 9: Test the stopping condition.  330 L. Parthiban et al. / J. Biomedical Science and Engineering 2 (2009) 323-335 SciRes Copyright © 2009 JBiSE The map formation occurs in two phases: required training patterns and a reduction in the training times of the classifier. Problem with linear PCA net- works is evident when the input data contains outliers. Outliers are individual pieces of data that are far re- moved from the data clusters (i.e., noise). They tend to distort the estimation of the eigenvectors and create skewed data projections. a) Initial formation of perfect (correct) order b) Final convergence. The second phase takes a longer duration than the first phase and requires a small value of learning rate. The learning rate is a slowly decreasing function of time and the radius of the neighborhood around a cluster unit also decreases as the clustering process goes on. The initial weights are assumed with random values. The learning rate is updated by α(t+1) = 0.5α(t). 5) Principal Component Analysis PCA network combine unsupervised and supervised learning in the same topology. PCA is an unsupervised linear procedure that finds a set of uncorrelated features, principal components, from the input. A MLP is super- vised to perform the nonlinear classification from these components. PCA is a technique that finds an orthogonal set of directions in the input space and provides a way to find the projections into these directions in an ordered fashion. The orthogonal directions are called eigen vec- tors of the correlation matrix of the input vector and the projections of the corresponding eigen values. a) Ordering of the principal components PCA must transform the input samples into a new space (the feature space) such that the information about the samples is kept, but the dimensionality is reduced. From the input space, it finds an orthogonal set of P directions where the input data has the largest energy, and extracts P projections from these directions in an ordered fashion. The first principal component is the projection, which has the largest value (think of the projections as the shadow of the data clusters in each direction as in Figure 7), while the Pth principal component has the smallest value. If the largest projections are extracted, then the most significant information about the input data is kept. This segment of the network computes the eigenvectors of the input’s cor- relation function without ever computing the correlation function itself. The outputs of the PCA layer are therefore related to the eigenvalues and can be used as input fea- tures to the supervised segment for classification. Since many of these eigenvalues are usually small, only the M (M<P) largest values need to be kept. This speeds up training even more. The importance of PCA analysis is that the number of inputs for the MLP classifier can be significantly re- duced. This results in a reduction of the number of Figure 7. Ordering of the principal components. 6) Initializing Neural Networks with Stern Series A Calkin-Wilf tree is a special type of binary tree ob- tained by starting with the fraction 11 and iteratively adding )( baa and bba )( below each fraction ba . The Stern-Brocot tree is closely related, putting )( baa and )( bab below each fractionba . Both trees generate every rational number. Writing out the terms in sequence gives 1/1, 1/2, 2/1, 1/3, 3/2, 2/3, 3/1, 1/4, 4/3, 3/5, 5/2, 2/5, 5/3, 3/4, 4/1,… as shown in Fig- ure 8. The sequence has the property that each denominator is the next numerator [26] and is known as Stern's dia- tomic series represented mathematically as a(0) = 0, a(1) = 1; for n >= 0, a(2n) = a(n), a(2n+1) = a(n) + a(n+1). As an array the terms are: 1,2 1,3,2,3 1,4,3,5,2,5,3,4 1,5,4,7,3,8,5,7,2,7,5,8,3,7,4,5 and so on . Finding 1/ [a(n)*a(n+1)] for each row R=1 ½, ½ R=2 1/3,1/6,1/6,1/3 R=3 1/4,1/12,1/15,1/10,1/10,1/15,1/12,1/4 and so on. Depending on the importance of a specific attribute chosen, we can initialize the weight of neural network with stern series for quick training. A tree showing the designed stern series for weight initialization is shown below in Figure 9. The main impact of initializing the neural network weight with stern series is quick training period .The code for generating Stern series is given below. Figure 8. Stern-brocot tree.  L. Parthiban et al. / J. Biomedical Science and Engineering 2 (2009) 323-335 331 SciRes Copyright © 2009 Figure 9. Weight initialization using stern sequence. #include<iostream.h> #include<conio.h> static int ans=0; //STERN'S RESULT void stern(int n) JBiSE { if(n==0||n==1) //STERN'S ASSUMTION { ans+=n; } else if(n%2==0) //STERN'S EVEN { n=n/2; if(n>1) { stern(n); } else { ans+=n;} } else //STERN'S ODD { n=n/2; stern(n); stern(n+1); } } void main() { textcolor(WHITE); textbackground(BLUE); clrscr(); int n; //STERN'S N CANFIS combines Classification and Regression Trees (CART) and the Neuro-Fuzzy Inference System (NFIS) in a two step procedure. CART is a tree-based algorithm used to optimize the process of selecting relevant pre- dictors from a large pool of potential predictors. Using the selected predictors, NFIS builds a model for con- tinuous output of the predictand. In this sense, CANFIS migrates various degrees of neuro-fuzzy spectrum be- tween the two extremes: a completely understandable FIS and a black-box NN, which is at the other end of interpretability spectrum. Neuro-fuzzy models can be characterized by neuro-fuzzy spectrum, in light of lin- guistic transparency and input-output mapping precision. gotoxy(33,3); cprintf("STERN'S SERIES\n\n"); gotoxy(2,5); cprintf("VALUE N: "); cin>>n; cout<<endl; for(int i=1;i<=n;i++) { ans=0; stern(i); gotoxy(2,wherey()); cprintf("%d/",ans); ans=0; stern(i+1); cprintf("%d\n",ans); } getch(); } 7) Experiments for Implementation of Classifiers The key design decisions for the neural networks used in the classification are the architecture and the training process. The adequate functioning of neural networks depends on the sizes of the training and the testing set. To comparatively evaluate the performance of the classi- fiers, all the classifiers presented in this paper were trained by the same training data set and tested with the evaluation data set. In order to compare the performance of the different classifiers for the same classification problem, in addition to CANFIS, we also implemented the MLPNN, PNN, PCA, SVM, and SOM. We per- formed different experiments during implementation of the classifiers and the number of hidden neurons was determined by taking into consideration the classifica- tion accuracies. In the hidden layers and the output lay- ers, the activation function used was the sigmoidal func- tion. The sigmoidal function with the range between zero and one introduces two important properties. First, the sigmoid is nonlinear, allowing the network to per- form complex mappings of input to output vector spaces, and secondly, it is continuous and differentiable, which allows the gradient of the error to be used in updating the weights. The training algorithm for different classifi- ers is based on adjusting all the weights between the neurons to minimize the mean square error of all the training patterns. The Levenberg-Marquardt algorithm is used for training the classifiers as it combines the best features of Gauss-Newton technique and steep- est-descent algorithm and does not suffer from slow convergence [19]. 3. DIAGNOSTIC SYSTEM USING CANFIS CANFIS powerful capability stems from pattern-de- pendent weights between consequent layer and fuzzy association layer. Membership values correspond to those dynamically changeable weights that depend on input patterns. CANFIS bears a close relationship to the computational paradigms of radial basis function (RBF) networks and modular networks. The fundamental component for CANFIS is a fuzzy neuron that applies membership functions (MFs) to the inputs. Two membership functions commonly used are general Bell and Gaussian. The network also contains a 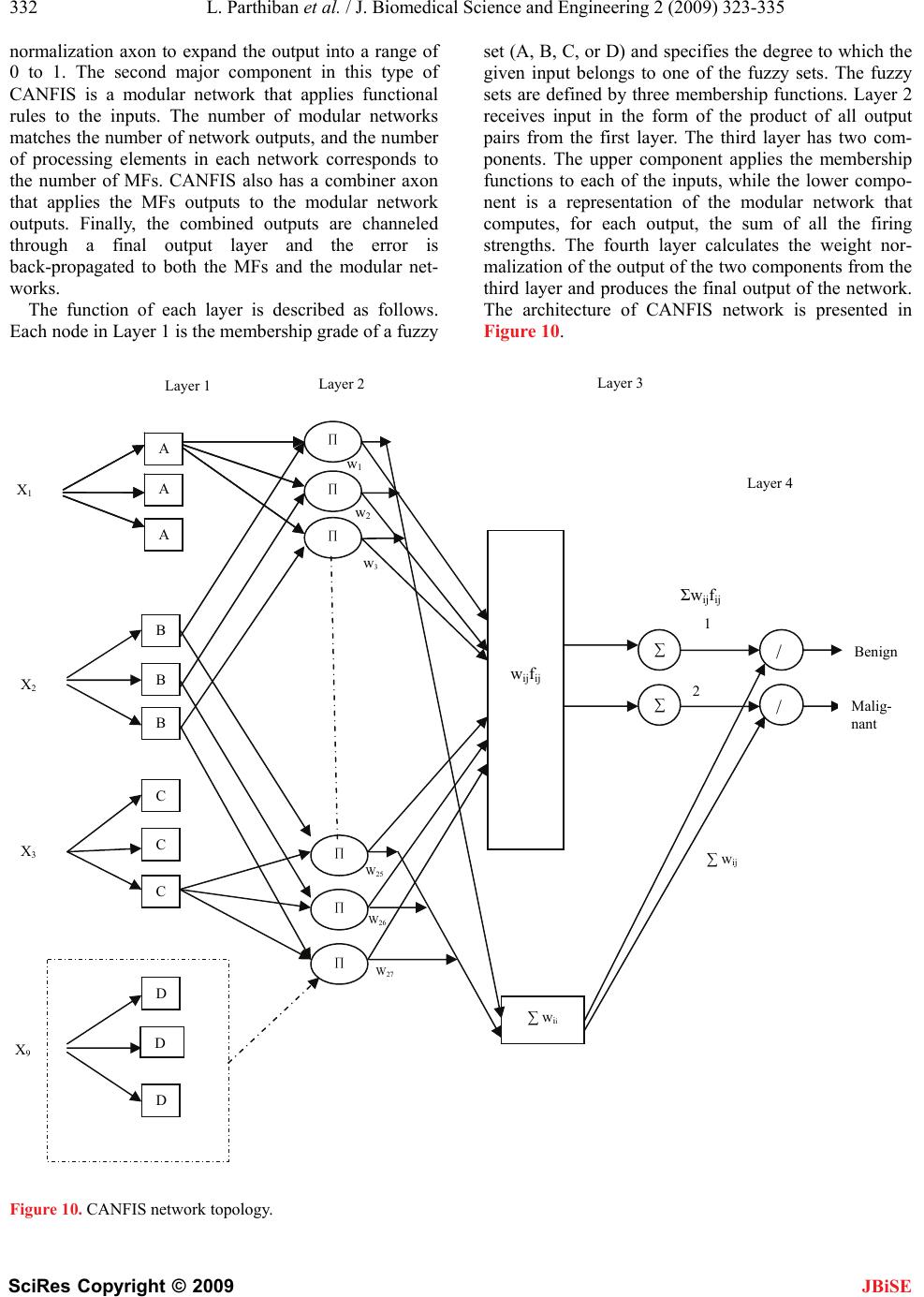 332 L. Parthiban et al. / J. Biomedical Science and Engineering 2 (2009) 323-335 SciRes Copyright © 2009 normalization axon to expand the output into a range of 0 to 1. The second major component in this type of CANFIS is a modular network that applies functional rules to the inputs. The number of modular networks matches the number of network outputs, and the number of processing elements in each network corresponds to the number of MFs. CANFIS also has a combiner axon that applies the MFs outputs to the modular network outputs. Finally, the combined outputs are channeled through a final output layer and the error is back-propagated to both the MFs and the modular net- works. The function of each layer is described as follows. Each node in Layer 1 is the membership grade of a fuzzy set (A, B, C, or D) and specifies the degree to which the given input belongs to one of the fuzzy sets. The fuzzy sets are defined by three membership functions. Layer 2 receives input in the form of the product of all output pairs from the first layer. The third layer has two com- ponents. The upper component applies the membership functions to each of the inputs, while the lower compo- nent is a representation of the modular network that computes, for each output, the sum of all the firing strengths. The fourth layer calculates the weight nor- malization of the output of the two components from the third layer and produces the final output of the network. The architecture of CANFIS network is presented in Figure 10. JBiSE F igure 10. CANFIS network topology. 1 2 ∑ wij ∑ wii W25 W27 W26 Malig- nan Benign Layer 4 w3 w2 w1 ∏ ∏ ∏ Layer 2 A A A La er Σwijfij ∑ ∑ Layer 3 Layer 1 wijfij D D D X9 B B B C C C ∏ ∏ ∏ A X3 X2 A X1 A 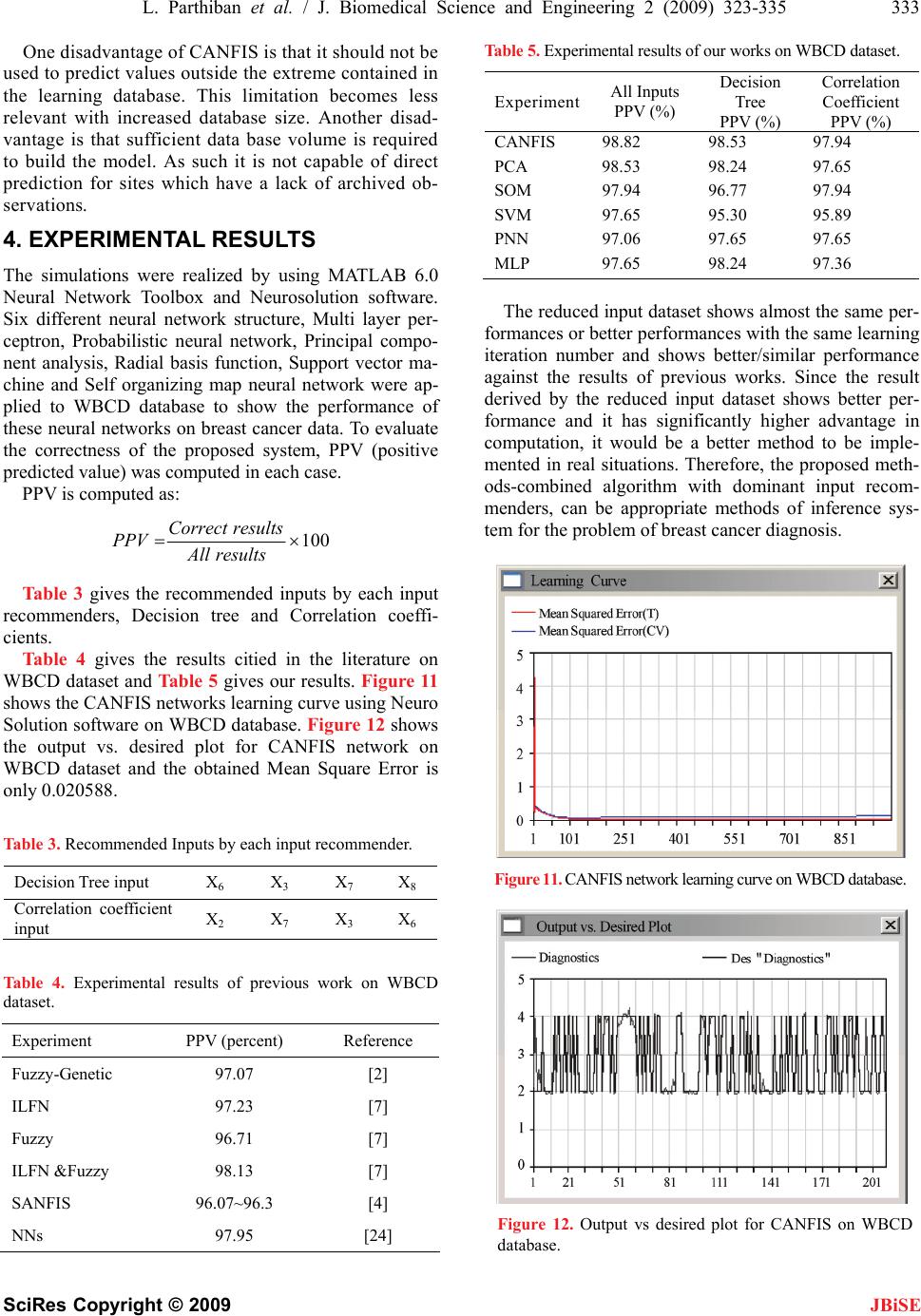 L. Parthiban et al. / J. Biomedical Science and Engineering 2 (2009) 323-335 333 SciRes Copyright © 2009 JBiSE One disadvantage of CANFIS is that it should not be used to predict values outside the extreme contained in the learning database. This limitation becomes less relevant with increased database size. Another disad- vantage is that sufficient data base volume is required to build the model. As such it is not capable of direct prediction for sites which have a lack of archived ob- servations. 4. EXPERIMENTAL RESULTS The simulations were realized by using MATLAB 6.0 Neural Network Toolbox and Neurosolution software. Six different neural network structure, Multi layer per- ceptron, Probabilistic neural network, Principal compo- nent analysis, Radial basis function, Support vector ma- chine and Self organizing map neural network were ap- plied to WBCD database to show the performance of these neural networks on breast cancer data. To evaluate the correctness of the proposed system, PPV (positive predicted value) was computed in each case. PPV is computed as: 100 resultsAll resultsCorrect PPV Table 3 gives the recommended inputs by each input recommenders, Decision tree and Correlation coeffi- cients. Table 4 gives the results citied in the literature on WBCD dataset and Table 5 gives our results. Figure 11 shows the CANFIS networks learning curve using Neuro Solution software on WBCD database. Figure 12 shows the output vs. desired plot for CANFIS network on WBCD dataset and the obtained Mean Square Error is only 0.020588. Table 3. Recommended Inputs by each input recommender. Decision Tree input X6 X 3 X 7 X 8 Correlation coefficient input X2 X 7 X 3 X 6 Table 4. Experimental results of previous work on WBCD dataset. Experiment PPV (percent) Reference Fuzzy-Genetic 97.07 [2] ILFN 97.23 [7] Fuzzy 96.71 [7] ILFN &Fuzzy 98.13 [7] SANFIS 96.07~96.3 [4] NNs 97.95 [24] Table 5. Experimental results of our works on WBCD dataset. Experiment All Inputs PPV (%) Decision Tree PPV (%) Correlation Coefficient PPV (%) CANFIS 98.82 98.53 97.94 PCA 98.53 98.24 97.65 SOM 97.94 96.77 97.94 SVM 97.65 95.30 95.89 PNN 97.06 97.65 97.65 MLP 97.65 98.24 97.36 The reduced input dataset shows almost the same per- formances or better performances with the same learning iteration number and shows better/similar performance against the results of previous works. Since the result derived by the reduced input dataset shows better per- formance and it has significantly higher advantage in computation, it would be a better method to be imple- mented in real situations. Therefore, the proposed meth- ods-combined algorithm with dominant input recom- menders, can be appropriate methods of inference sys- tem for the problem of breast cancer diagnosis. Figure 11. CANFIS network learning curve on WBCD database. Figure 12. Output vs desired plot for CANFIS on WBCD database.  334 L. Parthiban et al. / J. Biomedical Science and Engineering 2 (2009) 323-335 SciRes Copyright © 2009 JBiSE 5. DISCUSSION Based on the results of the present paper, we would like to highlight the following. 1) The high classification accuracies of CANFIS with full data give insights into the nine measures of the WBCD database. This classification accuracy slightly decreases with input recommenders. 2) The classification accuracy of PCA, SOM, PNN and MLP does not change much even after decreasing the inputs with input recommenders. 3) When we initialized the weight of neural network using stern series instead of zero as we usually do, the speed of training was noted to increase. 4) During SVM training, most of the computational effort is spent on solving the quadratic programming problem in order to find the support vectors. The SVM maps the features to higher dimensional space and then uses an optimal hyperplane in the mapped space. This implies that though the original features carry adequate information for good classification, mapping to a higher dimensional feature space could potentially provide bet- ter discriminatory clues that are not present in the origi- nal feature space. The selection of suitable kernel func- tion appears to be a trial-and-error process. One would not know the suitability of a kernel function and per- formance of the SVM until one has tried and tested with representative data. For training the SVMs with RBF- kernel functions, one has to predetermine the σ values. The optimal or near optimal σ values can only be ascer- tained after trying out several, or even many values. 5) The pattern layer of a PNN often consists of all training samples of which many could be redundant. Including redundant samples can potentially lead to a large network structure, which, in turn, induces two problems. First, it would result in a higher computational overhead simply because the amount of computation necessary to classify an unknown pattern is proportional to the size of the network. Second, a consequence of a large network structure is that the classifier tends to be oversensitive to the training data and is likely to exhibit poor generalization capabilities to the unseen data. However, the smoothing parameter also plays a crucial role in the PNN classifier, and an appropriate smoothing parameter is often data dependent. 6. CONCLUSIONS In this work, the performance of various neural network structures was investigated for breast cancer diagnosis problem. Initializing Neural network with Stern series was proposed to speed up training. CANFIS is the best trade off between neural networks and fuzzy logic pro- viding smoothness and adaptability. It also gives better classification accuracy in terms of PPV [Table 5] than all other neural classifiers analyzed. The performance of the SVM was not as high as the SOM and PCA. This may be attributed to several factors including the train- ing algorithms, estimation of the network parameters, and the scattered and mixed nature of the features. The results of the present paper demonstrated that the CAN- FIS and PCA can be used in the classification of the WBCD data by taking into consideration the misclassi- fication rates. This work also indicates that CANFIS can be effectively used for breast cancer diagnosis to help oncologists. REFERENCES [1] Ioanna, C., Evalgelos, D., and George, K., (2000) Fast detection of masses in computer aided mammography, IEEE Signal Processing Magazine: January, 54–64. [2] Pena-Reyes, C. A. and Sipper, M., (91999) A fuzzy-ge- netic approach to breast cancer diagnosis, Artificial Intel- ligence in Medicine, 131–155. [3] Pena-Reyes, C. A. and Sipper, M., (1998) Evolving fuzzy rules for breast cancer diagnosis, In Proceedings of 1998 International Symposium on Nonlinear Theory and Ap- plications. [4] Wang, J.-S. and Lee, G. C. S., (2002) Self-adaptive neu- ron-fuzzy inference systems for classification applica- tions, IEEE Transactions on Fuzzy Systems. [5] Arulampalam, G. and Bouzerdoum, A., (2001) Applica- tion of shunting inhibitory artificial neural networks to medical diagnosis, Seventh Australian and New Zealand Intelligent Information Systems Conference. [6] Land, W. H., Jr., Masters, T., and Lo, J. Y., (2000) Appli- cation of a new evolutionary programming/adaptive boosting hybrid to breast cancer diagnosis, IEEE Con- gress on Evolutionary Computation Proceedings. [7] Meesad, P. and Yen, G. G., (2003) Combined numerical and linguistic knowledge representation and its applica- tion to medical diagnosis, IEEE Transactions on Systems, Man, and Cybernatics. [8] Jang, J.-S. R., (1993) ANFIS: Adaptive-network based fuzzy inference system., IEEE Trans. on System, Man and Cybernetics, 23(3). [9] Jang, J. R. and Sun, C. T. (1995) Neuro-fuzzy modeling and control, Proceedings of the IEEE. [10] Freund, Y. and Schapire, R. E., (1996) Experiments with a new boosting algorithm, Machine Learning: Proceed- ings of the Thirteenth International Conference. [11] Schapire, R. E., (1999) Theoretical views of boosting and applications, Proceedings of Algorithmic Learning The- ory. [12] Sebri, A., Malek, J., and Tourki, R., (2007) Automated breast cancer diagonosis based on GVF-snake segmenta- tion, wavelet features extraction and neural network clas- sification, J. Computer Science, 3(8), 600–607. [13] Goldberg, D., (1989) Genetic algorithm in search, opti- mization, and machine learning, Addison-Wesley. [14] John, G. H., Kohavi, R., and Pfleger, K., (1994) Irrele- vant features and the subset selection problem, Machine Learning: Proceedings of the Eleventh International Conference.  L. Parthiban et al. / J. Biomedical Science and Engineering 2 (2009) 323-335 335 SciRes Copyright © 2009 JBiSE [15] Mangasarian, O. L., Street, W. N., and Wolberg, W. H., (1994) Breast cancer diagnosis and prognosis via linear programming, Mathematical Programming Technical Report 9410, University of Wisconsin. [16] Song, H.-J., Lee, S.-G., and Park, G.-T., (2005) A Meth- odology of computer aided diagnostic system on breast cancer, Proceedings of the IEEE Conference on Control Applications Toronto, Canada. [17] Haykin, S., (1994) Neural networks: A comprehensive foundation, NewYork: Macmillan. [18] Chaudhuri, B. B. and Bhattacharya, U., (2000) Efficient training and improved performance of multilayer percep- tron in pattern classification, Neurocomputing, 34, 11– 27. [19] Hagan, M. T. and Menhaj, M. B., (1994) Training feed- forward networks with the Marquardt algorithm, IEEE Trans. Neural Netw., 5(6), 989–993. [20] Specht, D. F., (1990) Probabilistic neural networks, Neu- ral Netw., 3(1), 109–118. [21] Burrascano, P., (1991) Learning vector quantization for the probabilistic neural network, IEEE Trans. Neural Netw., 2(4), 458–461. [22] Vapnik, V., (1995) The Nature of statistical learning the- ory, NewYork: Springer-Verlag. [23] Cortes and Vapnik, (1995) Support vector networks, Mach. Learn., 20(3), 273–297. [24] Setiono, R., (2000) Generating concise and accurate clas- sification rules for breast cancer diagnosis, Artificial In- telligence in Medicine. [25] American Cancer Society Hompage, (20 July 2008) Cit- ing Internet sources URL: http://www.cancer.org. [26] Johnson, M. B., (2003) Sterns diatomic array applied to fibonacci representations, Fibonacci Quarterly 41, 169– 180. Appendix AdaBoost Adaptive Boosting AP Accuracy Percentage CAD Computer Aided Diagnosis CANFIS Coactive Neuro-Fuzzy Inference Systems CART Classification and Regression Trees DT Decision Tree FIS Fuzzy Inference Systems GA Genetic Algorithm MLPNN Multi Layer Perceptron Neural Network NFIS Neuro-Fuzzy Inference System NN Neural Network PCA Principal Component Analysis PNN Probabilistic Neural Network PPV Positive Predicted Value RMS Root Mean Square SOM Self Organizing Map SVM Support Vector Machine WBCD Wisconsin Breast Cancer Data
|