Open Journal of Social Sciences
Vol.04 No.05(2016), Article ID:66830,7 pages
10.4236/jss.2016.45004
On the Foundations of Guidelines for Health Economic Assessment
Hans Keiding
Department of Economics, University of Copenhagen, Copenhagen, Denmark

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 11 April 2016; accepted 13 May 2016; published 16 May 2016

ABSTRACT
In recent years, increased attention has been given to guidelines for cost-effectiveness analysis of medical interventions, and some of these guidelines (such as NICE [1]) have become rather influential. In the paper, we present a model of retrieving and processing information to be used for the study of guidelines and their use. Our main result, which relies on a version of the theorem of Blackwell [2], shows that in cases where there are sufficiently many decisions to be made on the basis of the information obtained, there can be no other objective ranking of methods than the trivial one ranking more information is higher than less information. In our context, this means that guidelines may have administrative advantages but cannot be considered as a scientifically based approach to better decision making.
Keywords:
Cost-Effectiveness, Value of Information, Blackwell’s Theorem, Guidelines

1. Introduction
In the course of the last decades, the use of cost-effectiveness analysis as an aid to decision making in healthcare has been increasing steadily, so as to become a standard feature of medical research and medical decision making. Parallel to this, there has been a discussion of methods and foundations (see e.g. Johannesson and Weinstein [3], Dolan and Edlin [4], Meltzer and Smith [5]), although to a much smaller extent. Among the issues, which have been debated is the possibility of drawing up official guidelines for carrying out a cost-effectiveness analysis. Such guidelines have indeed been established and put to use, and in these one may observe a trend towards specification in greater detail of what must be done in order that the resulting cost-effectiveness analysis can be considered as satisfactory. This may perhaps be seen partly as a response to a demand from the pharmaceutical industry wanting exact instructions as to which documentation should be presented, partly by authorities looking for a precise set of rules regarding the information to be demanded from producers applying for market permit or drug reimbursement.
In many cases, the scientific community has been invited to participate in drawing up guidelines, so that the cost-effectiveness analyses which are made in accordance with the guidelines are those that are “best” from a purely theoretical point of view. The question of whether such scientifically correct guidelines can at all be found seems not to have attracted much, if any, attention. However, a similar question has been asked long ago in another field, which however is related, namely that of finding the “correct” accounting standards, rules for how the accounts of a company should be drawn up and presented. As pointed out by Demski [6], such correct accounting standards simply do not exist.
What is behind this seemingly paradoxical situation―that science cannot point to the right way of doing cost-effectiveness analysis―is a problem, which was considered by statistical information theory even earlier. Indeed, one of the main results of this theory, known as Blackwell’s theorem (Blackwell, [2]), states that if a decision maker has to choose an act with uncertain consequences, and she has a choice of different methods for obtaining information prior to this choice, then the only ranking of such information services which does not depend on the preferences of the decision maker is the simple, but unfortunately quite trivial rule: “More information is better than less”. In other words, there can be no method for collecting and presenting information which is superior to all other methods no matter how the decision maker looks at the outcomes.
It might be argued that this dependence of the guidelines on the decision maker is not a real problem; guidelines are indeed established by specified decision makers (public health care organizations, NICE, and others). However, in what follows we can actually sharpen the statement of Blackwell’s theorem slightly, so that it will apply even when the decision maker and her preferences are uniquely specified, as long as there are sufficiently many alternative actions to choose among―as will indeed be the case when the decision maker is in charge of a national health care system. So, even in this case, there is no theoretical foundation of guidelines considered as “golden standard” or best practice. Guidelines may be convenient or useful for many other purposes, but alas, they cannot be the last of science. This result adds another dimension to the skepticism towards the increased emphasis on detailed guidelines, as expressed e.g. by Birch and Gafni [7].
The paper is structured as follows: In Section 2, we introduce the statistical information theory and explain the relation to cost-effectiveness analysis. This section ends with a formulation and proof of the version of Blackwell’s theorem, which is tailored to our purpose. In Section 3, we connect the abstract result on information methods to cost-effectiveness analysis, and we show why guidelines cannot be scientifically well-founded here, although it may well be so in purely medical decision making. We close the paper with some comments in Section 4.
2. Cost-Effectiveness Analysis as an Information Service
In the present section, we briefly introduce the background for our model, which is the approach to the theory of information introduced by Marschak, Blackwell, and others, see e.g. Marschak and Miyasawa [8]; a more detailed exposition of this theory can be found in Hirshleifer and Riley [9]. The model introduced pertains to all decision making under uncertainty, but we keep the discussion as close as possible to our principal application, which is cost-effectiveness analysis, showing as we proceed how the abstract concepts fit in with our overall purpose.
We consider a situation where a decision maker―which in our application may be a health care organization deciding upon the best way of treating the patients under their responsibility―has to make a decision which is subject to some uncertainty. This uncertainty will be modeled in a very simple way, since we assume that there is a finite set of uncertain states, 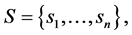 each of which affect the results of the treatment. The choices of the decision maker is given by a set A of decisions; for our purposes, a decision is a function
each of which affect the results of the treatment. The choices of the decision maker is given by a set A of decisions; for our purposes, a decision is a function 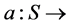 X, taking each uncertain state
X, taking each uncertain state 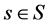 to an outcome
to an outcome 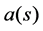 in a space of possible outcomes (to be specified later). In our application to health care, a decision is a particular treatment of patients (which may be a procedure in hospital or the administration of a particular medical drug); the effects of such treatments are usually not fully known, and neither are their costs. In our present case, we have assumed that there are some identifiable but random factors which are behind this uncertainty, which is indeed a simplification as compared with reality where the uncertainty about future consequences of a treatment tend to have a more complex nature. However, this simple structure allows us to obtain some results, which hopefully give insight into the more complicated reality.
in a space of possible outcomes (to be specified later). In our application to health care, a decision is a particular treatment of patients (which may be a procedure in hospital or the administration of a particular medical drug); the effects of such treatments are usually not fully known, and neither are their costs. In our present case, we have assumed that there are some identifiable but random factors which are behind this uncertainty, which is indeed a simplification as compared with reality where the uncertainty about future consequences of a treatment tend to have a more complex nature. However, this simple structure allows us to obtain some results, which hopefully give insight into the more complicated reality.
We shall assume that the decision maker has initial beliefs about the likelihood of each of the underlying states 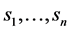 influencing outcome of the decisions, formulated as a (“prior”) probability distribution
influencing outcome of the decisions, formulated as a (“prior”) probability distribution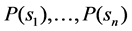 . Also, the decision cares about the consequences obtained, meaning that she has a utility function
. Also, the decision cares about the consequences obtained, meaning that she has a utility function 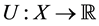 assigning utility or degree of satisfaction to each possible outcome. Relying only on the initial beliefs, standard decision making under uncertainty calls for the choice of decision which maximizes expected utilityinitial beliefs, standard decision making under uncertainty calls for the choice of decision which maximizes expected utility
assigning utility or degree of satisfaction to each possible outcome. Relying only on the initial beliefs, standard decision making under uncertainty calls for the choice of decision which maximizes expected utilityinitial beliefs, standard decision making under uncertainty calls for the choice of decision which maximizes expected utility

over all decisions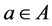 . This behavior may not correspond fully to what decision makers in healthcare organizations actually do, but it is at least in line which what they pretend to do.
. This behavior may not correspond fully to what decision makers in healthcare organizations actually do, but it is at least in line which what they pretend to do.
In our discussion so far, there has been no mentioning of information; decisions were based on assessments of probabilities but not on any observation; to allow for this―and thereby formally introducing “evidence-based medicine” into the model, we should add the option of collecting and processing of information before the decision is made, which is what cost-effectiveness analysis is about. In particular, following the recent guidelines of NICE [1], information about the medical effects of a treatment should be gathered, if possible by a randomized clinical trial, which should also contain observations about health-related quality of life, and the information should be collected and processed according the specified rules. What the guidelines specify, is an information method, that is a procedure for collecting date and producing a signal (in our case, a report of the cost-effec- tiveness analysis, containing relevant cost-effectiveness ratios as well as other ingredients (such as sensitivity analysis, confidence limits etc.)
In our simplified formal world, an information method is a pair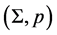 , where
, where 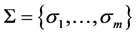 is a finite
is a finite
set if signals, and  is a system of conditional probabilities
is a system of conditional probabilities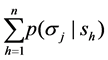 , for
, for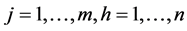 , inter-
, inter-
preted as the probability that signal 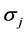 is reported given that the true state of nature is
is reported given that the true state of nature is
Given any observed signal

where 

babilities over states of nature, conditional on the observed signal
over all



that is the difference between the ex ante expected utility with and without the information method. We call 
The value of information, as derived above, depended on the utility function U of the decision maker. Consequently, the choice of information method, if indeed such a choice is open to the decision maker, will in its turn depend on the utility function. In the case we have in mind, where an information method is a particular way of collecting and presenting data on different medical interventions, this means that the method for performing these operations should be chosen in accordance with the desires and goals of the decision maker. Simple and acceptable as this sounds, it carries a controversial message, namely that it is in general impossible to prescribe a single such method, independent of the decision maker who is going to use the results. In other word, ranking different methods of performing cost-effectiveness analysis seems not in general possible without recourse to a concrete decision maker, so that guidelines, which are applicable to all users cannot be constructed in a scientific way. In the following we give the precise formulation of this result.
For this, we need the notion that one information method is more informative that another. Let 




signal 



An equivalent formulation of this condition is that there is an 
where 







Theorem 1. Let 






(i) 

(ii) 

Proof: (ii)






By separation of convex sets, there must then be

Now we use the assumption on 




since 

Assessing the value of the information method 
It follows that
(i)




Therefore, if 

where we have used that 

and summing over
and it follows that
3. Conditions for Meaningfulness of Guidelines
In the previous section, we established a version of Blackwell’s theorem tailored to our problem, dealing with cost-effectiveness analysis in general and rules for conducting such analyses in particular. In the present section, we draw the lines from the abstract world of information systems to the more relevant context of guidelines for cost-effectiveness analysis―as well as to guidelines for other aspects of medical decision-making.
For this, we take a closer look on the conditions on 
For this, we consider the environment in which a cost-effectiveness analysis is carried out. We outline briefly its theoretical background (or rather, one possible theoretical background, as there may be several, cf. Brouwer and Koopmanschap [14]): We consider medical interventions (in a broad sense) in a society with M individuals, each characterized by a vector 





In the standard approach (Hansen, Hougaard, Keiding, Østerdal, [15]) it is assumed that each individual i has a utility function defined on the consumption-health pairs

an approach often termed as “welfarist”. In our present setup, we do not insist that allocations are ranked exactly in this way, but only that the decisions in society are made in accordance with a utility function of the type
To make this setup fit with our model of the previous section, we assume that the changes in allocation are subject to random displacements, so that 



Theorem 2. Let A be a set of interventions of the form 
(i) A allows for all possible money compensations of health effects: For each intervention



(ii) for each

If the cost-effectiveness methodology 




Proof: The theorem is basically a reformulation of Theorem 1 and all that is needed is to show that A contains interventions such that for each vector

But this follows easily from the assumptions (i) and (ii), which together show that there is an intervention, constructed from the original one combined with suitable commodity displacements in each state, such that the final utility level in each state corresponds to the vector
It may be noticed that our assumptions in Theorem 2 are stronger than what is really needed; indeed, we need not compensate everybody, what matters is only that some compensations can be made which make up for any loss and gain that the decision maker would experience from the uncompensated intervention. Also, it suffices to consider very small displacements since what mattered in Theorem 1 was not the absolute values of the utilities in each state but only their relative values.
4. Discussion
The implications for practice of the results are that guidelines for cost-effectiveness are of dubious value., at least when considered as a source of information. Given that the assumptions of Theorem 2 are reasonably weak and seem satisfied in practical situations where cost-effectiveness analysis is performed, the conclusion is that there can be no “best” way of setting up such an analysis. The reference case approach, specifying that observations on medical and other outcomes of an intervention should be carried out according to a standardized scheme, may have administrative merits but it has no scientific basis. The only rule that can be stated is that more detailed observation is better than less detailed information, which indeed is trivial.
Why, then, are guidelines so widespread and estimated? Again, Theorem 2 points to an answer: For purely medical interventions, the setup differs considerably from that of cost-effectiveness analysis, since there is no economic component, and obviously monetary transfers are irrelevant for the medical outcome. In such cases, information methods may indeed by ranked to an extent which permits a choice of a best one, singled out as a reference case.
What makes perfect sense in one context may however not necessarily work in another. Guidelines may be useful in medical practice and misleading in economic practice. The arguments of the present paper should indicate why this may be the case.
Cite this paper
Hans Keiding, (2016) On the Foundations of Guidelines for Health Economic Assessment. Open Journal of Social Sciences,04,20-26. doi: 10.4236/jss.2016.45004
References
- 1. NICE (2013) Guide to the Methods of Technology Appraisal 2013. http://publications.nice.org.uk/pmg9
- 2. Blackwell, D. (1951) Comparison of Experiments. Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability, University of California Press, 99-102.
- 3. Johannesson, M. and Weinstein, M.C. (1982) On the Decision Rules of Cost-Effectiveness Analysis. Journal of Health Economics, 12, 459-467. http://dx.doi.org/10.1016/0167-6296(93)90005-Y
- 4. GiaDolan, P. and Edlin, R. (2002) Is It Really Possible to Build a Bridge between Cost-Benefit Analysis and Cost- Effectiveness Analysis. Journal of Health Economics, 21, 827-843. http://dx.doi.org/10.1016/S0167-6296(02)00011-5
- 5. Meltzer, D.O. and Smith, P.C. (2011) Theroetical Issues Rel-evant to the Economic Evaluation of Health Technologies. In: Pauly, M.V., McGuire, T.G. and Barros, P.P., Eds., Handbook of Health Economics, Vol. 2, Elsevier, 433-469.
- 6. Demski, J. (1973) The General Impossibility of Normative Accounting Standards, The Accounting Review. October 1973, 718-723.
- 7. Birch, S. and Gafni, A. (2006) Information Created to Evade Reality (ICER)—Things We Should Not Look to for Answers. Pharmaco Economics, 24, 1121-1131.
- 8. Marschak, J. and Miyasawa, K. (1968) Economic Comparability of Information Systems. International Economic Review, 9, 137-174. http://dx.doi.org/10.2307/2525472
- 9. Hirshleifer, J. and Riley, J.G. (1992) The Analytics of Uncertainty and Information. Cambridge University Press, Cambridge.
- 10. Drummond, M.F. and McGuire, A. (2001) Economic Evaluation in Health Care: Merging Theory with Practice, Oxford University Press, Oxford.
- 11. Drummond, M.F., Sculpher, M.J., Torrance, G.W., O’Brien, B.J. and Stoddart, G.L. (2005) Methods for the Economic Evaluation of Health Care Programmes. 3rd Edition, Oxford University Press, Oxford.
- 12. Muenig P. (2007) Cost-Effectiveness Analysis in Health: A Practical Approach. 2nd Edition, Wiley, New York.
- 13. Biel-inska-Kwapisz, A. (2003) Sufficiency in Blackwell’s Theorem. Mathematical Social Sciences, 46, 21-25. http://dx.doi.org/10.1016/S0165-4896(03)00004-0
- 14. Brouwer, W.B.F. and Koopmanschap, M.F. (2000) On the Economic Foundation of CEA. Ladies and Gentlemen, Take Your Positions. Journal of Health Economics, 19, 439-459. http://dx.doi.org/10.1016/S0167-6296(99)00038-7
- 15. Hansen, B.O., Hougaard, J.L., Keiding, H. and Osterdal, L.P. (2004) On the Possibility of a Bridge between CEA and CBA, Comments on a Paper by Dolan and Edlin. Journal of Health Economics, 23, 887-898. http://dx.doi.org/10.1016/j.jhealeco.2003.10.002




























