Journal of Computer and Communications
Vol.04 No.05(2016), Article ID:66758,7 pages
10.4236/jcc.2016.45008
Exploring the Big Data Using a Rigorous and Quantitative Causality Analysis
X. San Liang
School of Marine Sciences and School of Mathematics, Nanjing University of Information Science and Technology, Nanjing, China




Received 28 April 2016; accepted 19 May 2016; published 26 May 2016
ABSTRACT
Causal analysis is a powerful tool to unravel the data complexity and hence provide clues to achieving, say, better platform design, efficient interoperability and service management, etc. Data science will surely benefit from the advancement in this field. Here we introduce into this community a recent finding in physics on causality and the subsequent rigorous and quantitative causality analysis. The resulting formula is concise in form, involving only the common statistics namely sample covariance. A corollary is that causation implies correlation, but not vice versa, resolving the long-standing philosophical debate over correlation versus causation. The applicability to big data analysis is validated with time series purportedly generated with hidden processes. As a demonstration, a preliminary application to the gross domestic product (GDP) data of United States, China, and Japan reveals some subtle USA-China-Japan relations in certain periods.
Keywords:
Causality, Big Data, Information Flow, Time Series, Causal Network

1. Introduction
We have entered an era of data wealth; how to analyze these data has become a big problem for scientists in the twenty-first century. This raises many challenging issues, among which is causal inference, a field which actually forms an important subject in many different scientific disciplines, even in philosophy (e.g., [1]). For data science, it will help to unravel the complexity of the ever-growing datasets, and hence help to build platforms for efficient management and better service.
Causality analysis, however, is a very challenging problem. In their book Doing Data Science (p. 274) [2], O’Neil and Schutt remarked, “One of the biggest statistical challenges, from both a theoretical and practical perspective, is establishing a causal relationship between two variables.” In the past few years, there has been a surge of interest in this field, echoing the call from the newly emerged science of big data. Many empirical or half-empirical formalisms have been proposed, and they generally work well in their specific contexts (see the references in [3]).
Recently, a rigorous and quantitative analysis has been developed to address the challenge (cf. [3], hereafter Liang 14, and [4]). It is found that causality analysis, which traditionally has been formulated as a statistical hypothesis testing (e.g., [5]), is actually a problem in physics; causality is actually a real physical notion, which can be put on a rigorous footing. With the Liang14 formalism, many problems, which traditional approaches fail to handle, turn out to be easy. It also unambiguously and explicitly resolves the long-standing debate in philosophy regarding correlation versus causation, and has been successfully applied to many real world problems.
However, this line of work has not even been touched in big data studies. While we should avail ourselves of the arsenal of traditional tools, new ideas, particularly new ideas like this one which is based firmly on physical footing, will for sure facilitate the advancement of the new science. We are therefore motivated to introduce the newly developed causality analysis to data scientists. This makes the main purpose of this study.
In the following we first give a brief review of the formalism, its development and major results. To test its utility in handling big data, in Section 3 we purportedly generate series in extreme situations, particularly series in the presence of hidden processes. As a demonstration, Section 4 presents a preliminary application to the study of the USA-China-Japan relation. This study is summarized in Section 4.
2. Theoretical Development and Applications
Historically Granger [5] formulated causality analysis as a statistical hypothesis test, which has now been referred to as Granger causality analysis. On the other hand, another real physical notion, namely, information flow, or information transfer as it may appear in the literature, has been developed for over three decades. Information flow has applications in a wide variety of disciplines; people gradually realize that central at the field, which makes it widely applicable, turns out to be its logical association to causality. This observation has further been substantiated as it was established that Granger causality and the most popular empirical measure of information flow so far, namely, transfer entropy [6], is actually equivalent [7].
So the two major lines of work on causality analysis eventually merge. The corresponding formalisms, however, have long been found unable to verify themselves in many applications, or they may even yield spurious causal relations. The verification is based on the following observation:
If the evolution of a variable, say, X1, is independent of another one, X2, then the causality from X2 to X1 vanishes.
Hereafter we will call it Principle of Nil Causality. Recently, Smirnov [8] gave this a systematic investigation, and concluded that they cannot verify the principle in a wide range of situations; similar results also show in [9]. In response to the call from the new science of big data, we should touch the base and re-examine the problem carefully.
Since causality can be quantitatively measured by information flow, while information flow is a real physical notion (not just something in statistics), Liang argued that it should be formulated on a rigorous footing, rather than be proposed as an ansatz [3] [10]. Besides, the above principle should be stated as a proven theorem, not something to be verified in applications. In this spirit, Liang [10] considered a stochastic system in the form
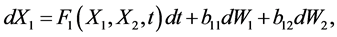 (1)
(1)
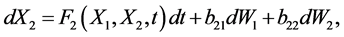 (2)
(2)
where (W1, W2) is a vector of standard Wiener process, and F1 and F2 are differentiable functions of (X1, X2). He obtained the following theorems:
Theorem 2.1. (Liang, 2008)
For the dynamical system (1)-(2), the rate of information flowing from X2 to X1 is
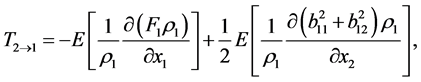 (3)
(3)
where E stands for mathematical expectation, and 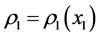 is the marginal probability density of X1.
is the marginal probability density of X1.
Theorem 2.2. Principle of nil causality (Liang, 2008)
If in the system (1)-(2), neither F1 nor b11 nor b12 has dependence on X2, then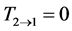 .
.
Note both are proven theorems (proofs are referred to [10]). Particularly, the second is just the principle of nil causality.
If only two time series are given, the information flow between them can be obtained through maximum likelihood estimation.
Theorem 2.3. (Liang, 2014)
Given two time series X1 and X2, under the assumption of a linear model, the maximum likelihood estimator (mle) of the rate of information flowing from X2 to X1 is
 (4)
(4)
In this equation,  is the sample covariance matrix between time series X1 and X2, and
is the sample covariance matrix between time series X1 and X2, and 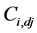 the sample covariance between Xi and a series derived from Xj using Euler forward differencing scheme:
the sample covariance between Xi and a series derived from Xj using Euler forward differencing scheme:
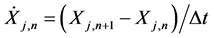 .
.
Note in (4) the T is actually the mle of the information flow, and, strictly, should bear a hat. We abuse the notation here as, from now on, only (4) will be used, and hence no confusion will arise. That is to say, (4) will be taken as the quantitative measure of causality from X2 to X1. More precisely, the absolute value of T measures the causality. When , X2 is causal to X1; if
, X2 is causal to X1; if , X2 is not the cause of X1.
, X2 is not the cause of X1.
The formula for information flow hence causality is very concise. Considering that in history there is a long-standing debate over correlation versus causation, one may transform it into a form in terms of correlation coefficient:
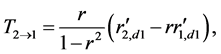 (5)
(5)
with  the correlation coefficient, and
the correlation coefficient, and 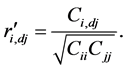 Observe that, if
Observe that, if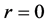 , then
, then ; but if
; but if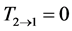 , r does not necessarily vanish. Contrapositively, this means that
, r does not necessarily vanish. Contrapositively, this means that
Causation implies correlation, but correlation does not imply causation.
Causality can be normalized so as to reveal its relative magnitude; see [4] for details. One may also perform statistical significance test for Equation (4), which is referred to [3].
Equation (4) has been validated with touchstone problems that fail the traditional Granger causality analysis. It has also been applied to many real world problems, with remarkable success. Among these applications is the causal structure study between CO2 and global warming [11]. It is found that the CO2 concentration rise during the past 120 years does cause the recent global warming; the causal relation is one-way, i.e., from CO2 to global atmosphere temperature. However, on a 1000-year (or over) scale, the causality is totally reversed; i.e., it is global warming that causes CO2 to increase, in agreement with that inferred from the ice-core data recently from Antarctica. Besides, the anthropogenic gas emission mainly from the Northern Hemisphere, however, causes mainly the warming in the Southern Hemisphere.
Another application is with several series of prices of US stocks downloaded from
significant causal relation can be interpreted based on common sense. For example, Ford is found to have a much larger causality to Wal-Mart than to CVS the convenience store chain, since, in the States, people rely on motor vehicles to shop at Wal-Mart stores, while CVS stores could be within walking distances. A deeper study shows that the causality generally varies with time. For GE and IBM, overall it seems that they are not significantly causal to each other. However, if we do a running time analysis, it is found that there is a very strong, almost one-way causality from IBM to GE in 70’s, starting from 1971. This identified causal structure change reveals to us an old story about “Seven Dwarfs and a Giant” in 1960s: GE was once the biggest computer user besides the U.S. Federal Government; to avoid relying on IBM, it began to manufacture mainframe computers, together with six other companies, competing for the computer market with IBM the Giant. But in 1970, GE sold its computer division. Starting from 1971, it then had to rely on IBM again. That is the reason why there is such an abrupt one-way causality jump from 1970 to 1971. While the story has almost gone to oblivion, this finding, which is solely based on the analysis of a couple of stock price time series, is really remarkable.
3. Validations
3.1. Validation with Series Generated with a Pair of Processes
Consider the series generated from two autoregressive processes, which traditionally have been used to test causality analysis tools,


where


The series generated for case I are shown in Figure 1. By visual inspection they are correlated and look alike. This is not surprising, as Y drives X hence X follows Y. As regards the causalities, since



For case II, 
To test the validity of (4), we design a case (case III) with very weak coupling:
In order to see whether the negligible causalities can be detected between series immersed in noises, we amplify e1 and e2 by ten times:


Table 1. Absolute information flow rates for the series generated with (6)-(7), and their respective confidence intervals at a 90% significance level. Units are in 10−4 nats per iteration.
Figure 1. Series generated for Case I in Table 1.
3.2. Validation with Series in the Presence of a Hidden Process
Our causality analysis is for two time series and, as we showed above, works perfectly for series generated with two processes. However, in real problems, a pair of time series could be the result of a lot of processes, and, moreover, we may have no idea what the processes are, or even are unaware of the existence of those processes. Will (4) still work in this case? In other words, can our analysis work well just the same in the presence of a hidden process? This is a problem where the traditional analyses fail.
Consider a pair of series formed from the X and Y in the following autoregressive processes:



Different from (6)-(7), here both X and Y are dependent on a third variable Z.
Pretending that we have no idea about the existence of Z, we perform a causality analysis just as before with the series X and Y. Repeat the experiments in Table 1, and list the computed causalities in Table 2.
The results are just as one would expect. For example, case I is a one-way causal system, and the computed absolute information flow rates confirm this; in case II X and Y are independent, and the calculated causalties are essentially zero in both directions; for case III, the causalities do exist, although they are very small. In a word, our causality analysis is capable of handling the series in the presence of hidden processes, even in extreme cases. It then can be utilized for data analysis on a generic basis, and is hence expected to play a role in the new science of big data.
4. A Preliminary Application
As a demonstration, we now take a look at the GDP of USA, China, and Japan, the three economic powers. The data are from World Bank1, available every year from 1960 through 2014. Note it is by no means our intention to conduct a research on international bilateral relation, which requires an in-depth investigation of the related economics and politics and, above all, more reliable data with finer time resolution; we are just about to provide an example to demonstrate how the above new causality analysis tool may allow us to extract the information underlying the data which would be otherwise very difficult, if not impossible, to extract.
Since the GDPs of the three countries soar from 1960 to 2014, we choose to examine their annual growth rates. Shown in Figure 2 are these rates. By visual inspection of the data we can see that the American and Japanese GDP growths are highly correlated. But aside from this, it is hard to tell what a structure the three may have. Now our rigorous causality analysis comes to aid.
The validation in the preceding section allows us to examine the relations between the three countries regardless of the GDP data of the rest world, particularly, Europe, though we know the influence of the latter does exist. Since we need to do the covariance estimation, we pick a 40-year window to build the ensemble, and then do a running time estimation. This results in a time period 1980-1995 over which the causalities can be computed. A straightforward application of (4) yields these causalities, which we plot in Figure 3.
First look at Figure 3(a). Because of the small ensemble, most of the values are not significant at a 80% level. But the large ones, particularly some of 
For Figure 3(c), the evolutionary pattern is also remarkable. As we said, Japan has a GDP growth history highly correlated to that of USA. What makes the high correlation? We know a one-way causality from one series, say X1, to another, say X2, will result in a correlation, but a causality in the opposite direction, or a mutual
Table 2. Absolute information flow rates for the series generated with (8)-(9), and their respective confidence intervals at a 90% significance level. Units are in 10−4 nats per iteration.
Figure 2. GDP annual growth rates (%) since 1960. Data source: World Bank (http://data.worldbank.org/).
Figure 3. Causalities (absolute information flow rates) between China and USA (a), between China and Japan (b), and between USA and Japan (c). Units: nats/yr.
causality, will also make such a correlation. Here the figure shows that the three possibilities all exist in this particular application, nicely spanning different periods (approximately 1980-1987, 1987-1990, 1990-1995). This serves as an excellent example about correlation versus causation, though an explanation of the structure in Figure 3(c) requires more knowledge of the politics and economics in history about the two countries, which we leave to future studies.
5. Summary and Outlook
The emerging data science will for sure benefit from the advancement of other data-related disciplines. In this study, we introduce to the community a recently established rigorous and quantitative causality analysis to help unravel the complexity of big datasets, explore the underlying causal structures, and hence design efficient platforms for service and management purposes. To summarize, we here repeat the formula in Theorem 2.3 for causality estimation, that is, for series X1 and X2, the information flow from the latter to the former is estimated to be
with 


The above formalism, or Liang14 formalism as referred in the text, has been applied with remarkable success to many real problems. In this study, it has been validated with data series in the presence of hidden processes, and then exemplified with an analysis of the GDP data of USA, China, and Japan. Though the study is preliminary, the result is very encouraging, from an aspect demonstrating its power. This analysis tool is expected to play a role in the new interdisciplinary science, i.e., the science of big data.
Acknowledgements
This study was supported by the National Science Foundation of China under Grant No. 41276032, by Jiangsu Provincial Government through “2015 Jiangsu Program for Innovation Research and Entrepreneurship Groups” and the Jiangsu Chair Professorship, and by the State Oceanic Administration through the Special Program on Global Change and Air-Sea Interaction (GASI-IPOVAI-06).
Cite this paper
X. San Liang, (2016) Exploring the Big Data Using a Rigorous and Quantitative Causality Analysis. Journal of Computer and Communications,04,53-59. doi: 10.4236/jcc.2016.45008
References
- 1. Dempster, A.P. (1990) Causality and Statistics. J. of Statistical Planning & Inference, 25, 261-278. http://dx.doi.org/10.1016/0378-3758(90)90076-7
- 2. O’Neil, C. and Schutt, R. (2013) Doing Data Science: Straight Talk from the Frontier. O’Reilly, Cambridge.
- 3. Liang, X.S. (2014) Unraveling the Cause-Effect Relation between Time Series. Phys. Rev. E, 90, 052150. http://dx.doi.org/10.1103/PhysRevE.90.052150
- 4. Liang, X.S. (2015) Normalizing the Causality between Time Series. Phys. Rev. E, 92, 022126. http://dx.doi.org/10.1103/PhysRevE.92.022126
- 5. Granger, C. (1969) Investigating Causal Relations by Econometric Models and Cross-Spectral Methods. Econometrica, 37, 424. http://dx.doi.org/10.2307/1912791
- 6. Schreiber, T. (2000) Measuring Information Transfer. Phys. Rev. Lett., 85, 461-464. http://dx.doi.org/10.1103/PhysRevLett.85.461
- 7. Barnett, L., Barrett, A.B. and Seth, A.K. (2009) Granger Causality and Transfer Entropy Are Equivalent for Gaussian Variables. Phys. Rev. Lett., 103, 238701. http://dx.doi.org/10.1103/PhysRevLett.103.238701
- 8. Smirnov (2013) Spurious Causalities with Transfer Entropy. Phys. Rev. E, 87, 042917.
- 9. Lizier, J.T. and Prokopenko, M. (2010) Differentiating Information Transfer and Causal Effect. European Phys. J. B, 73, 605-615. http://dx.doi.org/10.1140/epjb/e2010-00034-5
- 10. Liang, X.S. (2008) Information Flow within Stochastic Dynamical Systems. Phys. Rev. E, 78, 031113. http://dx.doi.org/10.1103/PhysRevE.78.031113
- 11. Stips, A., Macias, D., Coughlan, C., Garcia-Gorriz, E. and Liang, X.S. (2016) On the Causal Structure between CO2 and Global Temperature. Scientific Reports, 6, 21691. http://dx.doi.org/10.1038/srep21691
NOTES
1Available at http://data.worldbank.org/.







