Intelligent Control and Automation, 2011, 2, 241-250
doi:10.4236/ica.2011.23029 Published Online August 2011 (http://www.SciRP.org/journal/ica)
Self-Structured Organizing Single-Input CMAC Control
for De-icing Robot Manipulator
Thanhquyen Ngo1,2, Yaonan Wang1, Youhui Chen1, Zan Xiao 1
1College of Electrical and Information Engineering, Hunan University, Changsha, China
2Faculty of Electrical Engineering, Ho Chi Minh City University of Industry, Ho Chi Minh, Vietnam
Received June 1, 2011; revised June 22, 2011; accepted June 29, 20 1 1
Abstract
This paper presents a self-structured organizing single-input control system based on differentiable cerebellar
model articulation controller (CMAC) for an n-link robot manipulator to achieve the high-precision position
tracking. In the proposed scheme, the single-input CMAC controller is solely used to control the plant, so the
input space dimension of CMAC can be simplified and no conventional controller is needed. The structure of
single-input CMAC will also be self-organized; that is, the layers of single-input CMAC will grow or prune
systematically and their receptive functions can be automatically adjusted. The online tuning laws of sin-
gle-input CMAC parameters are derived in gradient-descent learning method and the discrete-type Lyapunov
function is applied to determine the learning rates of the proposed control system so that the stability of the
system can be guaranteed. The simulation results of three-link De-icing robot manipulator are provided to
verify the effectiveness of the proposed control methodology.
Keywords: Cerebellar Model Articulation Controller (CMAC), De-icing Robot Manipulator,
Gradient-Descent Method, Self-Organizing, Signed Distance
1. Introduction
In general, robotic manipulators have to face various
uncertainties in their dynamics, such as friction and ex-
ternal disturbance. It is difficult to establish exactly
mathematical model for the design of a model-based
control system. In order to deal with this problem, the
braches of current control theories are broad including
classical control: neural networks (NNs) control [1-3],
adaptive fuzzy logic control (FLCs) [4-6] or adaptive
fuzzy-neural networks (FNNs) [7-9] etc. They are classi-
fied as adaptive intellig ent control b ased on conven tional
adaptive control techniques where fuzzy systems or neu-
ral networks are utilized to approximate a nonlinear
function of the dynamical systems. However, many
adaptive approaches are rejected as being overly compu-
tationally intensive because of the real-time parameter
identification and requ ired control design.
Fuzzy logic control (FLCs) has found extensive appli-
cations for plants that are complex and ill-defined which
is suitable for simple second order plants. However, in
case of complex higher order plants, all process states are
required as fuzzy input variables to implement state
feedback FLCs. All the state variables must be used to
represent contents of the rule antecedent. So, it requires a
huge number of control rules and much effort to create.
To address these issues, single-input Fuzzy Logic con-
trollers (S-FLC) was proposed for the identification and
control of complex dynamical systems [10-12]. As a re-
sult, the number of fuzzy rules is greatly reduced com-
pared to the ca se of t he conv enti onal F LCs, but i ts cont rol
performance is almost the same as conventional FLCs.
Neural networks (NNs) are a model-free approach,
which can approximate a nonlinear function to arbitrary
accuracy [1-3]. However, the learning speed of the NNs
is slow. To deal with these issues, cerebellar model ar-
ticulation controller (CMAC) was proposed by Albus in
1975 [13] for the identification and control of complex
dynamical systems, due to its advantage of fast learning
property, good generalization capability and ease of im-
plementation by hardware [13-15]. The conventional
CMACs, regarded as non-fully connected perceptron-like
associative memory network with overlapping receptive
fields which used constant binary or triangular functions.
The disadvantage is that their derivative information is
not preserved. For acquiring the derivative information of

T. NGO ET AL. 242
input and out put variables, C hiang and Lin [16] developed
a CMAC network with a differentiable Gaussian recep-
tive-field basis function and provided the convergence
analysis for t his network. The advantages of using CMAC
over neural network in many applications were well
documented [17-21]. However, in the above CMAC lit-
eratures, the structure of CMAC cannot be obtained
automati cally. The am ount of m emory space is difficult to
select, which will influence the learning and control
schemes. Some self-organizing CMAC neural networks
were proposed for structure adaptation [22-25]. In [22]
and [23] a data clustering technique is used to reduce the
memory size and a structural adaptation technique is
developed in order to accommodate new data sets.
However, only the structure growing mechanism is in-
troduced and; the pruning mechanism was not discussed.
In [24], a self-organizing hierarchical CMAC was intro-
duced. The authors proposed a multilayer hierarchical
CMAC model and used Shannon’s entropy measure and
golden-section search method to determine the input
space quantization. However, their approach is too com-
plicated and lacks online real-time adaptation ability.
Online adjusting suitable memory space of CMAC
structure is our motivation. To address these issues, C. M.
Lin, T. Y. Chen proposed self-organizing control system
[25]. This control system does not require prior knowl-
edge amount of memory space, the layers of CMAC will
grow or prune systematically. However, the dimension of
the input space of CMAC control system is reduced
through a comb in ation of sliding con tro l mode l. Recently,
to deal with the problem of the simplified input, B. J
Choi, S. W. Kwak and B. K. Kim proposed the S-FLC
[10-12] and its advantages which are mentioned above.
Based on the S-FLC, several literatures developed sin-
gle-input CMAC (S-CMAC) control system [26,27],
which adopts two learning stages, namely, an offline
learning stage and online learning stage. The disadvan-
tage is that their derivative information is also not pre-
served. So, M. F. Yeh and C. H. Tsai proposed differen-
tiable standalone CMAC control system [28] to provided
better system status in the learning control. In addition,
the quantization of input space could be reduced while
using the differentiable standalone CMAC. However, the
disadvantages are that the structure of S-CMAC cannot
be obtained automatic al l y .
In this paper, we propose a novel self-structured orga-
nizing single-input CMAC (SOSICM) control system for
three-link De-icing robot manipulator to achieve the
high-precision position tracking. This control system
combines advantages of S-CMAC and it does not require
prior knowledge of a certain amount of memory space,
and the self-organizing approach demonstrates the prop-
erties of generating and pruning the input layers auto-
matically. The developed self-organizing rule of S-CMAC
is clearly and easily used for real-time systems. More-
over, the developed system is solely used to control the
plant and no conventional or compensated controller.
The online tuning laws of CMAC parameters are derived
in gradient-descent method.
This paper is organized as follows: System description
is described in section 2. Section 3 presents SOSICM
control system. Numerical simulation results of a
three-link De-icing robot manipulator under the possible
occurrence of uncertainties are provided to demonstrate
the tracking control performance of the proposed
SOSICM system in section 4. Finally, conclusions are
drawn in section 5.
2. System Description
In general, the dynamic of an n-link robot manipulator
may be expressed in the Lagrange following form:




,MqqCqqqGq N



  (1)
where are the joint position, velocity and
acceleration vectors, respectively,
,, n qqq R


nn
M
qR

 denotes
the inertia matrix,


,nxn CqqR

1nx
NR
expresses the matrix
of centripetal and Coriolis forces, is the
gravity vector, represents the vector of exter-
nal disturbance , friction term

1nx
Gq R


l
t
f
q
, and un-modeled
dynamics, is the torque vectors exerting on
joints. In this paper, a new three-link De-icing robot ma-
nipulator, as shown in Figure 1, is utilized to verify dy-
namic properties are given in section 4.
1mx
R  
The control problem is to force


,
n
i
qt R
1, 2,im

 to track a given bounded reference input
signal


n
R
di
qt . Let be the tracking error
vector as follows:

i
et
, 1,2,
idii
eq qim

 (2)
and the system tracking error vector is defined as
De-icing Robot
Link 1Link 1
Link 2
Link 2
Link 3
Link 3
Link 2
Link 1
Power Line
Figure 1. Architecture of three-link De-icing robot manipu-
lator.

T. NGO ET AL.243

1
2
1
1
12
1
12
00
00
00 0
00
, 1,2,,
ii
ii
i
n
ni i
n
ii iinii
n
ii ni
ke
ke
ke
ke keke
im

 





















(3)
where nn
ni
K
R  is the scaling factor matrix for the
system tracking vector 1
[]
nn
iii i
eeee R


,

. 1, 2,im
Based on [10,11], the tracking error is trans-
formed into a single variable, termed the signed distance
which is the distance from an actual state
to the switching line as shown in Figure 2 for a
2-D input. The switching line is defined as follows:
n
iR
 
,
m
si
dRn
iR
 
12
121
0
nn
iniii
ee ee 




 (4)
where is a constant. Then, the signed dis-
tance between the switching line and operating point
can be expressed by the following equation:
1
1n nR



n
iR
 
12
1( 1)2211
222
121
1
nn
ninn iii
si
n
d

 








 (5)
According to the standalone CMAC control system is
shown in Figure 3. This control scheme provided better
i

i


0
si
d
0
si
d
si
d
),(
ii



0


i
i



Figure 2. Derivation of a signed distance.
d/dt
i

si
d
i
e
+
-
di
q
i
q
i
w

i
m

i


i2


i1

i
q
Signed
Distance
Adaptive
Law
Standalone Scheme
1
k
2
k
i
k
1

i
k
2

S-CMAC
Figure 3. Block diagram of standalone CMAC control sys-
tem.
control characteristics due to using the differentiable
CMAC in the system. The advantage is that derivative
information of input and output variables is preserved in
learning process. In addition, the generalization error
caused by quantization of input space could be reduced
while using the differentiable CMAC.
Based on the standalone CMAC control system, we
propose the SOSICM control system as shown in Figure
4, which combines advantages of standalone CMAC and
it does not require prior knowledge of a certain amount
of memory space. The self-organizing approach demon-
strates the properties of ge nerating and pruning the input
layers automatically. The developed self-organizing rule
of CMAC is clearly and easily used for real-time systems
3. Adaptive SOSICM Control System
3.1. Brief of the S-CMAC
An S-CMAC is proposed and shown in Figure 5. It is
composed of an input, association memory, weight and
output spaces. The signal propagation and the basic
function in each space are expressed as follows:
1) Input space
s
D; assume that each input state vari-
able
s
i can be quantized into d
s
i discrete states and
that the information of a quantized state is regarded as
region for each layer ki . Therefore, there exist
si
N
nth
1N

individual points on the
s
i- axis. Figure 6
shows the case of si
d
10N

. Each activated state in each
layer becomes a firing element, thus, the weight of each
layer can be obtained. The Gaussian basic function for
each layer is given as follows:
d/dt
si
d
i
e
+
-
di
q
i
q
i
w

i
m

i


i 2


i1

i
k
1

i
k
2

i
q
Signed
Distance
S-CMAC
Adaptive
Law
2
k
SOSICM Scheme
Self-Organizing of
S-CMAC Layers
i

ki

ki
v
ki
n
1
k
Learning
Rate
Propagation
Error Term
d/dt
i
e

i
e
pi

wi
P
i
P

i
k
P
1
i
k
P
2
mi
P
wi

mi

i 

i1

i 2

Figure 4. Block diagram of proposed SOSICM control sys-
tem.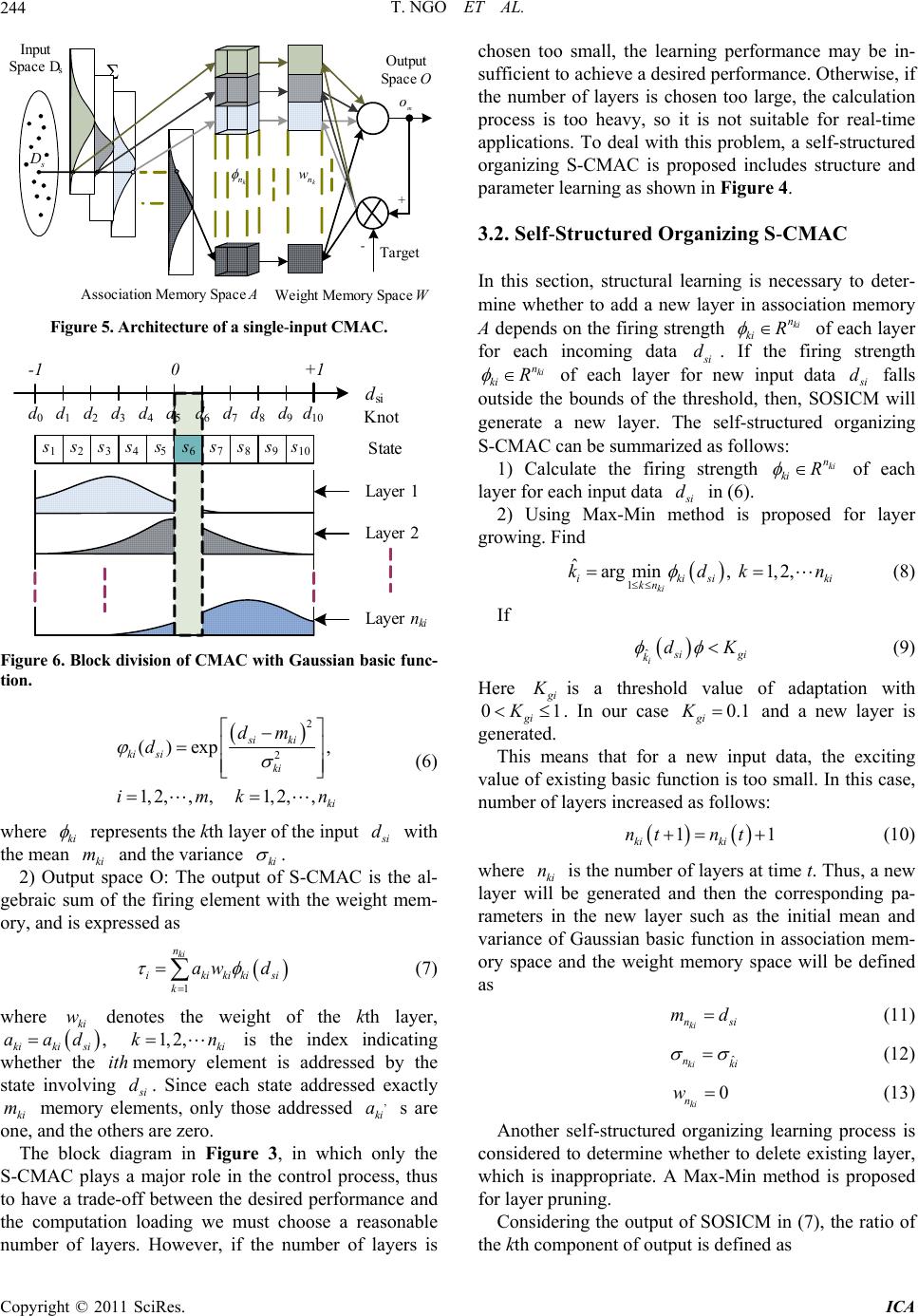

T. NGO ET AL. 244

k
n
w
m
o
k
n

s
D
Input
Space DsOutput
Space O
Weight Memory Space W
Association Memory Space A
Target
+
-
Figure 5. Architecture of a single-input CMAC.
d1d2d3d4d7d8d9d10
s1s2s3s4s5s7s8s9s10
dsi
-10 +1
Knot
State
Layer 1
Layer 2
Layer nki
d6 d5
s6
d0
Figure 6. Block divisio n of CMAC with Gaussian basic func-
tion.

2
2
()exp ,
1,2,,, 1,2,,
si ki
ki siki
ki
dm
d
imk






 n


(6)
where ki

represents the kth layer of the input
s
i
d w
the mean ki
m a the variance ki
ith
nd

.
2) Output space O: The output of S-CMAC is the al-
gebraic sum of the firing element with the weight mem-
ory, and is expressed as

1
ki
n
ikikiki
k
aw d 

si
n
(7)
where denotes the weight of the kth layer,
is the index indicating
whether the ith memory element is addressed by the
state involving
ki
w

si
d

,
ki ki
aa1, 2,ki k
s
i. Since each state addressed exactly
ki memory elements, only those addressed s are
one, and the others are zero.
d
m,
ki
a
The block diagram in Figure 3, in which only the
S-CMAC plays a major role in the control process, thus
to have a trade-off between the desired performance and
the computation loading we must choose a reasonable
number of layers. However, if the number of layers is
chosen too small, the learning performance may be in-
sufficient to achieve a desired performance. Otherwise, if
the number of layers is chosen too large, the calculation
process is too heavy, so it is not suitable for real-time
applications. To deal with this problem, a self-structured
organizing S-CMAC is proposed includes structure and
parameter learning as shown in Figure 4.
3.2. Self-Structured Organizing S-CMAC
In this section, structural learning is necessary to deter-
mine whether to add a new layer in association memory
A depends on the firing strength of each layer
for each incoming data
ki
n
ki R
 
s
i. If the firing strength
of each layer for new input data
d
ki
n
ki R
 
s
i falls
outside the bounds of the threshold, then, SOSICM will
generate a new layer. The self-structured organizing
S-CMAC can be summarized as follows:
d
1) Calculate the firing strength of each
layer for each input data
ki
n
ki R
 
s
i
2) Using Max-Min method is proposed for layer
growin g . F ind
d in (6).


1
ˆargmin, 1,2,
ki
ikisi
kn
kdk 

k n
i
(8)
If


ˆi
s
i
kdK
 gi (9)
Here
g
i
K
is a threshold value of adaptation with
0K1
gi

. In our case and a new layer is
generated. 0.1
gi
K
This means that for a new input data, the exciting
value of existing basic function is too small. In this case,
number of layers increased as follows:


1
ki ki
ntnt1

 (10)
where ki is the number of layers at time t. Thus, a new
layer will be generated and then the corresponding pa-
rameters in the new layer such as the initial mean and
variance of Gaussian basic function in association mem-
ory space and the weight memory space will be defined
as
n
ki
n
mdsi (11)
ˆ
ki
nki

  (12)
0
ki
n
w (13)
Another self-structured organizing learning process is
considered to determine whether to delete existing layer,
which is inappropriate. A Max-Min method is proposed
for layer pruning.
Considering the output of SOSICM in (7), the ratio of
the kth component of output is defined as

T. NGO ET AL.245
, 1,2,,
ki
ki ki
i
v
M
Mk

n
(14)
where ,
kikiki wv

 Then, the minimum ratio of the kth
component is defined as follows:
1
arg min
ki
i
kn
k


ki
MM (15)
If
ici
k
M
MK

 (16)
Here ci
K
is a predefined deleting threshold. In our
case and the i layer will be deleted.
This means that for an output data, if the minimum con-
tribution of a layer is less than the deleting threshold, then
this layer will be deleted.
0.03Kci kth

3.3. On-Line Learning Algorithm
The central part of the learning algorithm for a SOSICM
is how to choose the weight memory mean
variance ki
,
ki
w,
ki
m

of the Gaussian basic function. ni Are
the scaling factors of the error i e and the change of
error i, which will significantly affect the performance
of SOSICM. For achieving effective learning, an on-line
learning algorithm, which is derived using the supervised
gradient descent method, is introduced so that it can in
real-time adjust the parameters of SOSICM. The energy
function is defined as
k
e

i
E

22
1
22
idii
Eqq e
1
i
(17)
According to the energy function (17) and the system
structure in Figure 4, the error term to be propagated is
given by
iii
pi i
iii
EEq
e
q

i
i
q




 
(18)
where ii q

 represent the sensitivity of the plant
with respect to its input. With the energy function
the parameters updating law based on the normalized
gradient descent method can be deri ved as follows
,
i
E
1) The updating law for the weight memory can
be derived according to kth

ii
ki wiwi
kii ki
kiwi pi kisi
EE
ww
ad
i
w










(19)
where wi

is positive learning rate for the output
weight memory the connective weight can be up-
dated according to the following equation:
,
ki
w



1
kiki ki
wtwt w (20)
2) The mean and variance of the Gaussian basic
function can be also updated according to
kth


2
2
2
iii
ki miwi
kiiki
si ki
kimi piki kisiki
EE
mmm
dm
awd



 

 



(21)


2
3
2
iii
ki iwi
kii ki
si ki
kiipiki kisiki
EE
dm
awd



 

 

 



(22)
where mi

, i


are positive learning rates for the mean
and variance, respectively. The mean and variance can
be updated as follows:


1
kikiki
mtmt m

 (23)


1
kiki ki
tt



 (24)
3) Finally, the updating law for scaling factors can be
derived as follows:

2
1
1
222
121
2
1
ki
iiisi
ni nini
niisi ni
nsi ki
nipikiki kisi
kki
n
nni
n
EEd
kkdk
dm
aw d
e



 






 












(25)
where mi

is the learning rate, and it can be updated by
the following:


1
nini ni
ktkt k

 (26)
The plant sensitivity ii q


 in (18) can be calcu-
lated if the plant model is exactly known. However, the
plant model is unknown, so ii q

 can not obtained
in advance. To deal with this problem, in [28], a simple
approximation of the error term of the system can be use
as follows:
p
ii
ee
i


 (27)
3.4. Convergence Analysis
The update laws of Equations (19), (21), (22) and (25)
require a proper choice of the learning rates ,
wi

mi

,
,
i


and ni

in order to the convergence of the output
error is guaranteed; however, this is not easy which de-
pends on each person’s experience. To train the
S-CMAC effectively, the variable learning rates which
guarantee convergence of the output error are derived in
the following.
Defined a discrete-type Lyapunov function can be

T. NGO ET AL. 246
given by
 
2
1
2
ii
Vke k (28)
Thus, the change of the Lyapunov due to the training
process is obtained as
 
22
1
11
2
ii iii
VkVkVke ke k

 
 

(29)
where is represented by [28]  1kei
  
1
T
i
iiii i
ek
ekekek ekP
P

  



i
(30)
where represents the in the learning process, i
i
eP

denotes a change of an adjustable parameters. Using
Equation (18), we have

i ipiiii
PeP ek    and
ipiii
PEP

 
p
ipi ii
P

 , where
p
i

is the
learning rate for the parameter Pi.
Thus:
 
  

22
22
2
22
2
1
2
1
2
12
2
iii i
pi pipi pi
ii
i
ii ii
pi
ii
pi pipi
iii
Vkekekek
ek
ek Pek P
PekP
 



 







 














(31)
If the learning rate
p
i

is selected as:

2
2
02
p
ipii i
ek P     

i
(32)
Then therefore

0,
i
Vk



1,
ii
Vk Vk the
Lyapunov stability (system stability) and the conver-
gence of the tracking error could be guaranteed. In addi-
tion, the optimal learning rate can be found for achieving
faster convergence by taking the differential equation (31)
with respect to
p
i

and equals to zero. Finally, the op-
timal learning rate can be determined as follows:

2
2
1
p
ipii i
ek P  



i
 (33)
where i P
i

 for ,,
ikiki
Pwm ki

 and , it can be
obtained as: ni
k

,
i
wiki ki
ki
Pk a
w







2
2
s
iki
i
mikiki ki
ki ki
dm
Pk aw
m







2
3
2si ki
i
ikikiki
ki ki
dm
Pk aw









2
1
1
222
121
2
1
ki
ni
nsiki
i
kkikikisi
k
ni ki
n
nni
n
dm
Pkawd
k
e







 










(34)
4. Simulation Results
A three-link De-icing robot manipulator as shown in
Figure 1 is utilized in this paper to verify the effective-
ness of the proposed control scheme. The detailed system
parameters of this robot manipulator are given as: link
mass , lengths angular posi-
tions and displacement position
123
,,()mmmkg
,( )qqrad

12
,ll m,
12


3
dm
.
The parameters for the equation of motion (1) can be
represented as follow:

11 1213
21 2223
31 3233
MMM
MqM MM
MMM















22
11112212 111
22
322 2212
94 14
2
2
M
mlmcllllcs
mcllcll
 

22
2222321 1
1443 2
M
ml mlml
2332322
M
Mmcl


33 3
M
m
12132131 0MMMM



11 1213
21 2223
31 3233
CC C
CqC CC
CCC














112 1 2111
22
2 2 2232 222122
8
122 2
Cmllcsq
msclmsclsll q







22
212 2 2232 222121
122 2Cmsclmsclsll q
d
q
2232 23
Cmsl 
2332 22 2Cmsl


3232 22
Cmslq


12133133 0CCCC

 




1211 2 2
122 222 3
3
12
12
cclcl mg
Gqsslmclm g
mg





 






(35)
where 3 qR

and the shorthand notations


11
,cqcos


22
cos ,cq

1
sin 1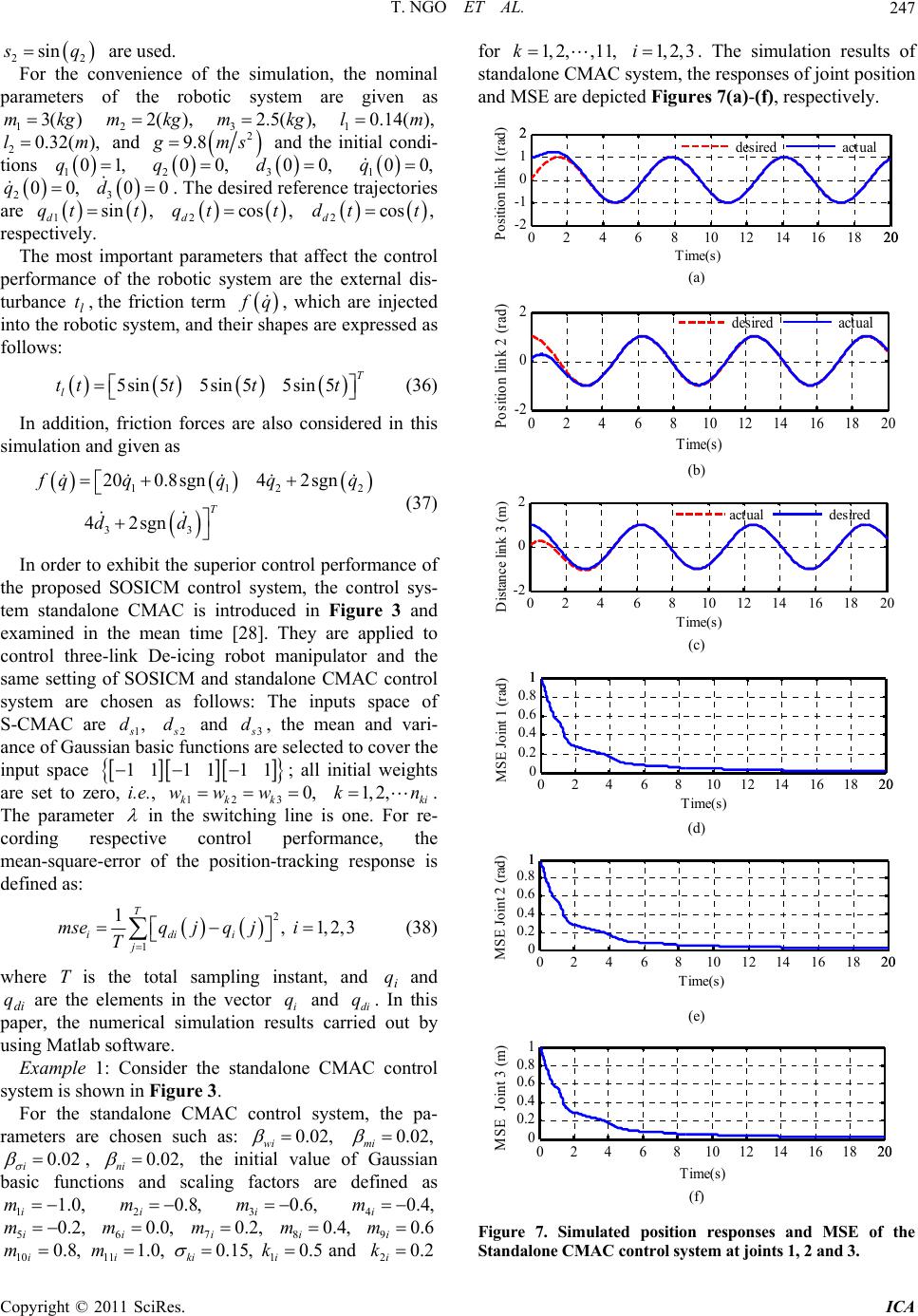
s
qand

T. NGO ET AL.247

2
sin 2
s
q
13( )mkg
are used.
For the convenience of the simulation, the nominal
parameters of the robotic system are given as
2 2(),mkg32.5( ),mkg

1
2 and 0.14(),lm
0.32(),lm

2
9.8
g
ms
00,3 d

01,

2
q and the initial condi- tions

1
q

00,


100q,



. The desired reference trajectories
are 1d

200,q
d


qt

300

sin ,t2d

cosqt

,t


2cos ,dt t d
respectively.
The most important parameters that affect the control
performance of the robotic system are the external dis-
turbance the friction term ,
l
t

f
q
, which are injected
into the robotic system, and their shapes are expressed as
follows:

l
tt

 
5sin55sin55sin5T t t t 

(36)
In addition, friction forces are also considered in this
simulation and given as
 

112
33
20 0.8sgn42sgn
42sgnT
2
f
qqqqq
dd
 





 (37)
In order to exhibit the superior control performance of
the proposed SOSICM control system, the control sys-
tem standalone CMAC is introduced in Figure 3 and
examined in the mean time [28]. They are applied to
control three-link De-icing robot manipulator and the
same setting of SOSICM and standalone CMAC control
system are chosen as follows: The inputs space of
S-CMAC are 1,
s
d 2
s
d and 3
s
d, the mean and vari-
ance of Gaussian basic functions are selected to cover the
input space







11
kkk
www
11 11
; all initial weights are set to zero, i.e., 123 .
The parameter 0,1,2,ki
kn

in the switching line is one. For re-
cording respective control performance, the
mean-square-error of the position-tracking response is
defined as:

2
1
1, 1,2,3
T
idii
j
mse
q
qjqj i
T
 

 (38)
where T is the total sampling instant, and iand
di are the elements in the vector i and di
q. In this
paper, the numerical simulation results carried out by
using Matlab software.
q
q
Example 1: Consider the standalone CMAC control
system is shown in Figure 3.
For the standalone CMAC control system, the pa-
rameters are chosen such as: 0.02,
wi

 0.02,
mi


0.02
i 

, 0.02,
ni


20.8 i
m
the initial value of Gaussian
basic functions and scaling factors are defined as
11.0, i
m ,30.6,
i
m 40.4,
i
m


,90.6
i
m
50.2, i
m 60.0,
i
m7 m0.2, 80.4
i
m
i

10 0.8, i
mm11 1.0,
iki 0.15,

10.5
i
kand 20.2
i
k

for 1, 2,,11,k

 1, 2, 3i

. The simulation results of
standalone CMAC system, the responses of joint position
and MSE are depicted Figures 7(a)-(f), respectively.
0 246810 1214 16182020
22
20
-2
-1
0
1
Time
Position link 1(rad)
desired actual
(
s
)
(a)
0 2 46 810 121416 18 20
-2
0
2
Time(s)
Position link 2 (r ad)
desired actual
(b)
0246810 1214161820
-2
0
2
Time
(
s
)
Distance link 3 (m)
actual des ired
(c)
0 2 46 810 12 1416 182020
0
0.2
0.4
0.6
0.8
11
Time(s)
MSE Joint 1 (rad)
(d)
0 246 810 1214 16 18 2020
0
0.2
0.4
0.6
0.8
11
Time
(
s
)
MSE Joint 2 (rad)
(e)
0 2 46 810 12 1416 182020
0
0.2
0.4
0.6
0.8
1
Time
(
s
)
MSE Joint 3 (m)
(f)
Figure 7. Simulated position responses and MSE of the
Standalone CMAC control system at joints 1, 2 and 3.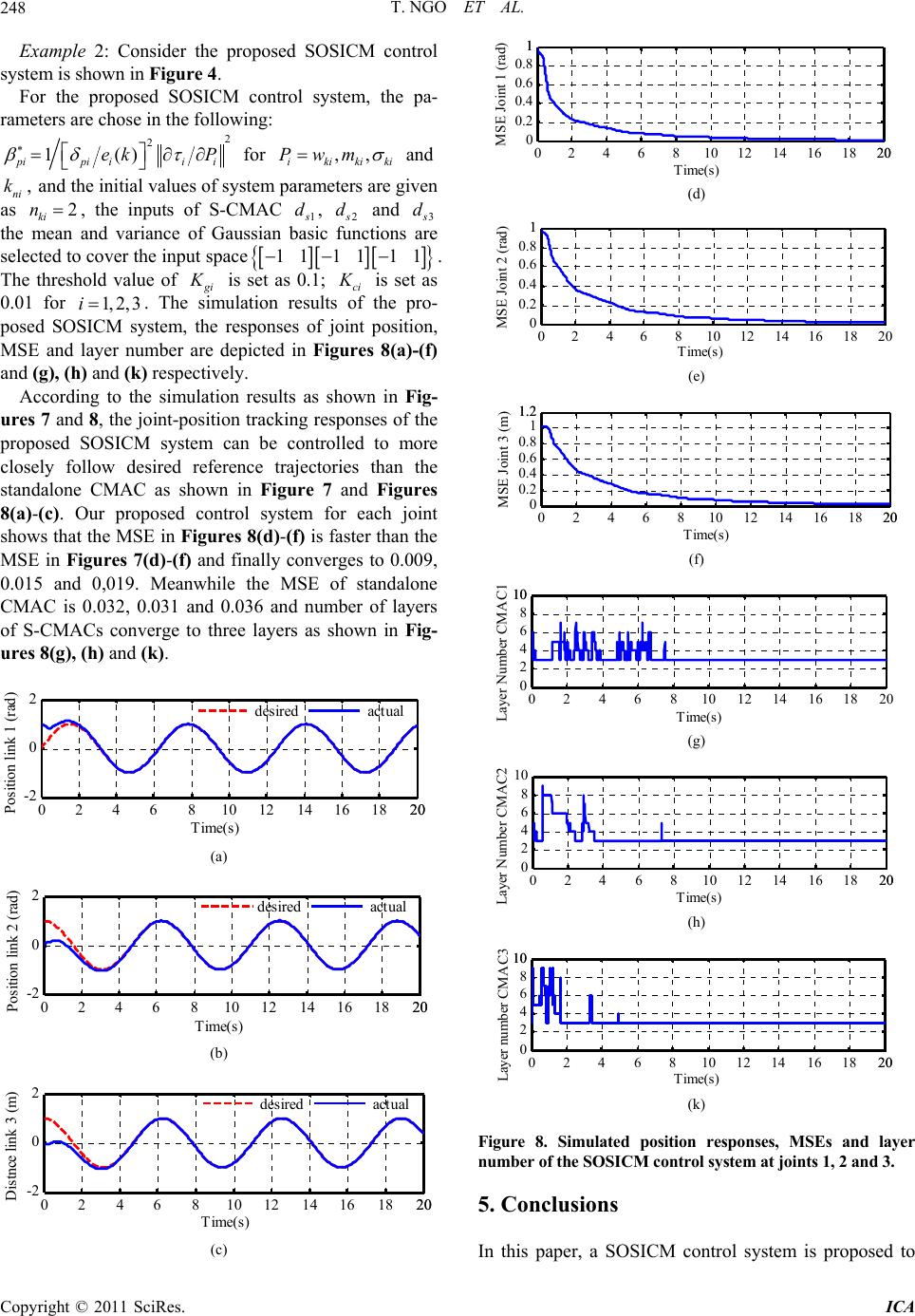

T. NGO ET AL. 248
Example 2: Consider the proposed SOSICM control
system is shown in Figure 4.
For the proposed SOSICM control system, the pa-
rameters are chose in the following:
2
2
1()
pipi iii
ek P  



ki for ,,
ikiki
Pwm

 and
ni , and the initial values of system parameters are given
as , the inputs of S-CMAC 1
k2
ki
n
s
d, 2
s
d and 3
s
d
the mean and variance of Gaussian basic functions are
selected to cover the input space







1111 11.
The threshold value of
g
i
K
is set as 0.1; ci
K
is set as
0.01 for . The simulation results of the pro-
posed SOSICM system, the responses of joint position,
MSE and layer number are depicted in Figures 8(a)-(f)
and (g), (h) and (k) respectively.
1, 2, 3 i
According to the simulation results as shown in Fig-
ures 7 and 8, the joint-position tracking responses of the
proposed SOSICM system can be controlled to more
closely follow desired reference trajectories than the
standalone CMAC as shown in Figure 7 and Figures
8(a)-(c). Our proposed control system for each joint
shows that the MSE in Figures 8(d)-(f) is faster than the
MSE in Figures 7(d)-(f) and finally converges to 0.009,
0.015 and 0,019. Meanwhile the MSE of standalone
CMAC is 0.032, 0.031 and 0.036 and number of layers
of S-CMACs converge to three layers as shown in Fig-
ures 8(g), (h) and (k).
0 2 4681012 14 16 18 2020
-2
0
2
Time(s)
Position link 1 (rad)
desired actual
(a)
0 2 4 6810 12 1416 18 2020
-2
0
2
Time(s)
Position link 2 (rad)
desired actual
(b)
0 24 6810 12 14 16 18 2020
-2
0
2
Time(s)
Distnce link 3 (m)
desired actual
(c)
0246810 12 14 1618 2020
0
0.2
0.4
0.6
0.8
11
Time
(
s
)
MSE Joint 1 (rad)
(d)
0246810 121416 18 20
0
0.2
0.4
0.6
0.8
11
Time(s)
MSE Joint 2 (rad)
(e)
0246810 12 14 16 182020
0
0.2
0.4
0.6
0.8
1
1.21.2
Time(s)
MSE Joint 3 ( m)
(f)
02 46 810 12 1416 1820
0
2
4
6
8
1010
Time
(
s
)
Laye r Number CMAC
1
(g)
0246810 12 14 16182020
0
2
4
6
8
10
Time(s)
Layer Number CMAC2
(h)
0246810 12 1416182020
0
2
4
6
8
1010
Time(s)
Layer number CMAC3
(k)
Figure 8. Simulated position responses, MSEs and layer
number of the SOSICM con trol system at joints 1, 2 and 3.
5. Conclusions
In this paper, a SOSICM control system is proposed to

T. NGO ET AL.249
control the joint position of a three-link De-icing robot
manipulator. In the SOSICM system, dynamical system
is completely unknown and auxiliary compensated con-
trol is not required in the control process. The online
tuning laws of S-CMAC parameters are derived in gra-
dient-descent learning method and the discrete-type
Lyapunov function is applied to determine the variable
optimal learning rates so that the stability of the system
can be guaranteed. This paper has successfully devel-
oped the SOSICM control system for a three-link
De-icing robot manipulator not only requires low mem-
ory with online structure and parameters tuning algo-
rithm, but also the input space can be reduced through
the signed distance. The simulation results of the pro-
posed SOSICM system can achieve favorable tracking
performance for three-link De-icing robot manipulator.
6. Acknowledgments
The authors would like to thank the editors and the re-
viewers for their valuable comments.
7. References
[1] A. Vemuri, M. M. Polycarpou and S. A. Diakourtis,
“Neural Network Based Fault Detection in Robotic Ma-
nipulators,” IEEE Robotics Automation, Vol. 14, No. 2,
1998, pp. 342-348. doi:10.1109/70.681254
[2] W. Z. Gao and R. R. Selmic, “Neural Network Control of
a Class of Nonlinear Systems with Actuator Saturation,”
American Control Conference, Boston, 2006, pp. 147-
156.
[3] Y. Zou, Y. N. Wang and X. Z. Liu, “Neural Network
Robust H∞Tracking Control Strategy for robot manipula-
tors,” Applied Mathematical Modelling, Vol. 34, No. 7,
2010, pp. 1823-1838. doi:10.1016/j.apm.2009.09.026
[4] B.-S. Chen, H.-J. Uang and C.-S. Tseng, “Robust Track-
ing Enhancement of Robot Systems Including Motor
Dynamics: A Fuzzy-Based Dynamic Game Approach,”
IEEE Transactions on Fuzzy Systems, Vol. 6, No. 4, 1998,
pp. 538-552. doi:10.1109/91.728449
[5] H.-X. Li and S.-C. Tong, “A Hybrid Adaptive Fuzzy
Control for a Class of Nonlinear MIMO Systems,” IEEE
Transactions on Fuzzy Sysemstm, Vol. 11, No. 1, 2003,
pp. 24-34. doi:10.1109/TFUZZ.2002.806314
[6] S. Labiod, M. S. Boucherit and T. M. Guerra, “Adaptive
Fuzzy Control of a Class of MIMO Nonlinear Systems,”
Fuzzy Set and Systems, Vol. 151, No. 1, 2005, pp. 59-77.
doi:10.1016/j.fss.2004.10.009
[7] Y. G. Leu, W. Y. Wang, and T. T. Lee, “Observe Based
Direct Adaptive Fuzzy Neural Control for Non-Affine
Nonlinear Systems,” IEEE Transactions on Neural Net-
works, Vol. 16, No. 4, 2005, pp. 853-861.
doi:10.1109/TNN.2005.849824
[8] R. J. Wai and Z. W. Yang, “Adaptive Fuzzy Neural Net-
work Control Design via a T-S Fuzzy Model for a Robot
Manipulator Including Actuator Dynamics,” IEEE Trans-
actions on Systems, Man and Cybernnetics, Vol. 38, No.
5, 2008, pp. 1326-1346.
doi:10.1109/TSMCB.2008.925749
[9] C.-S. Chen, “Dynamic Structure Neural Fuzzy Networks
for Robust Adaptive Control of Robot Manipulators,”
IEEE Transactions on Industrial Electronics, Vol. 55, No.
9, 2008, pp. 3402-3414. doi:10.1109/TIE.2008.926778
[10] B. J. Choi, S. W. Kwak and B. K. Kim, “Design of Sin-
gle-Input Fuzzy Logic Controller and Its Properties,”
Fuzzy Sets and Systems, Vol. 106, No. 3, 1999, pp.
299-308. doi:10.1016/S0165-0114(97)00283-2
[11] B. J. Choi, S. W. Kwak and B. K. Kim, “Design and Sta-
bility Analysis of Single-Input Fuzzy Logic Controller,”
IEEE Transactions on Systems, Man and Cybernnetics,
Vol. 30, No. 2, 2000, pp. 303-309.
doi:10.1109/3477.836378
[12] K. Ishaque, S. S. Abdullah, S. M. Ayob and Z. Salam,
“Single Input Fuzzy Logic Controller for Unmanned Un-
derwater Vehicle,” Journal of Intelligent and Robotic
Systems, Vol. 59, No. 3, 2010, pp. 87-100.
doi:10.1007/s10846-010-9395-x
[13] J. S. Albus, “A New Approach to Manipulator Control:
The Cerebellar Model Articulation Controller,” Journal
of Dynamic Systems Measurement and Control, Vol. 97,
No. 3, 1975, pp. 220-227. doi:10.1115/1.3426922
[14] H. Shiraishi, S. L. Ipri and D. D. Cho, “CMAC Neural
Network Controller for Fuel-Injection Systems,” IEEE
Transactions on Control Systems Technology, Vol. 3, No.
1, 1995, pp. 32-38. doi:10.1115/1.3426922
[15] S. Jagannathan, S. Commuri and F. L. Lewis, “Feedback
Linearization Using CMAC Neural Networks,” Auto-
matica, Vol. 34, No. 3, 1998, pp. 547-557.
doi:10.1016/S0005-1098(97)00206-9
[16] C. T. Chiang and C. S. Lin, “CMAC with General Basis
Functions,” Journal of Neural Networks, Vol. 9, No. 7,
1996, pp. 1199-1211.
doi:10.1016/S0005-1098(97)00206-9
[17] Y. H. Kim and F. L. Lewis, “Optimal Design of CMAC
Neural-Network Controller for Robot Manipulators,”
IEEE Transactions on Systems, Man and Cybernnetics,
Vol. 30, No. 1, 2000, pp. 22-31.
doi:10.1109/5326.827451
[18] C. M. Lin and Y. F. Peng, “Adaptive CMAC-Based Su-
pervisory Control for Uncertain Nonlinear Systems,”
IEEE Transactions on Systems, Man and Cybernnetics,
Vol. 34, No. 2, 2004, pp. 1248–1260.
doi:10.1109/TSMCB.2003.822281
[19] S. F. Su, T. Tao and T. H. Hung, “Credit Assigned
CMAC and Its Application to Online Learning Robust
Controllers,” IEEE Transactions on Systems, Man and
Cybernnetics, Vol. 33, No. 2, 2003, pp. 202-213.
doi:10.1109/TSMCB.2003.810447
[20] H.-C. Lu, C.-Y. Chuang and M.-F. Yeh, “Design of Hy-
brid Adaptive CMAC with Supervisory Controller for a
Class of Nonlinear System,” Neurocomputing, Vol. 72,
No. 7-9, 2009, pp. 1920-1933.

T. NGO ET AL. 250
doi:10.1016/j.neucom.2008.07.004
[21] Y. F. Peng and C. M. Lin, “Intelligent Hybrid Control for
Uncertain Nonlinear Systems Using a Recurrent Cerebel-
lar Model Articulation Controller,” IEEE Proceedings
Control Theory and Applications, Vol. 151, No. 5, 2004.
pp. 589-600. doi:10.1049/ip-cta:20040903
[22] J. Hu and F. Pratt, “Self-Organizing CMAC Neural Net-
works and Adaptive Dynamic Control,” IEEE Interna-
tional Symposium on Intelligent Control/Intelligent Sys-
tems and Semiotics, Cambridge, 1999, pp. 259-265.
[23] H. C. Lu and C. Y. Chuang, “Robust Parametric CMAC
with Self-Generating Design for Uncertain Nonlinear
Systems,” Neurocomputing, Vol. 74, No. 4, 2011, pp.
549-562. doi:10.1016/j.neucom.2010.09.001
[24] H. M. Lee, C. M. Chen and Y. F. Lu, “A Self-Organizing
HCMAC Neural-Network Classifier,” IEEE Transactions
on Neural Networks, Vol. 14, No. 1, 2003, pp. 15-27.
doi:10.1109/TNN.2002.806607
[25] C. M. Lin and T. Y. Chen, “Self-Organizing CMAC Con-
trol for a Class of MIMO Uncertain Nonlinear Systems,”
IEEE Transactions on Neural Networks, Vol. 20, No. 9,
2009, pp. 1377-1384. doi:10.1109/TNN.2009.2013852
[26] M.-F. Yeh, “Single-Input CMAC Control System,” Ne u -
rocomputing, Vol. 70, No. 16-18, 2007, pp. 2638-2644.
doi:10.1016/j.neucom.2006.05.019
[27] M.-F. Yeh, H.-C. Lu and J.-C. Chang, “Single-Input
CMAC Control System with Direct Control Ability,”
IEEE Transactions on Systems, Man and Cybernnetics,
Vol. 3, No. 1, 2006, pp. 2602-2607.
doi:10.1109/ICSMC.2006.385256
[28] M.-F. Yeh and C.-H. Tsai, “Standalone CMAC Control
Systems with Online Learning Ability,” IEEE Transac-
tions on Systems, Man and Cybernnetics, Vol. 40, No. 1,
2010, pp. 43-53. doi:10.1109/TSMCB.2009.2030334