Intelligent Control and Automation, 2011, 2, 214-225
doi:10.4236/ica.2011.23026 Published Online August 2011 (http://www.SciRP.org/journal/ica)
Motor Learning Based on the Cooperation of Cerebellum
and Basal Ganglia for a Self-Balancing Two-Wheeled Robot
Xiaogang Ruan, Jing Chen, Lizhen Dai
School of Electronic Information and Control Engineering, Beijing University of Technology, Beijing, China
Received May 23, 2011; revised May 30, 2011; accepted June 7, 2011
Abstract
A novel motor learning method is present based on the cooperation of the cerebellum and basal ganglia for
the behavior learning of agent. The motor learning method derives from the principle of CNS and operant
learning mechanism and it depends on the interactions between the basal ganglia and cerebellum. The whole
learning system is composed of evaluation mechanism, action selection mechanism, tropism mechanism. The
learning signals come from not only the Inferior Olive but also the Substantia Nigra in the beginning. The
speed of learning is increased as well as the failure time is reduced with the cerebellum as a supervisor.
Convergence can be guaranteed in the sense of entropy. With the proposed motor learning method, a motor
learning system for the self-balancing two-wheeled robot has been built using the RBF neural networks as
the actor and evaluation function approximator. The simulation experiments showed that the proposed motor
learning system achieved a better learning effect, so the motor learning based on the coordination of cere-
bellum and basal ganglia is effective.
Keywords: Motor Learning, Cerebellum, Basal Ganglia, Operant Learning, Self-Balancing Two-Wheeled
Robot
1. Introduction
Many skills and behaviors of human or animals are
formed and developed gradually in the self-learning and
self-organization process of nervous system. It is im-
portant to understand and imitate the internal learning
mechanism of human and animals’ nervous system, and
it is an important issue to give such a mechanism to ma-
chine for control science, artificial intelligence and ro-
botics study. Opposite with passive machinery reception
learning, autonomous learning is an active self-knowl-
edge and independent learning, and it is relatively the
basis of agent’s long-term learning and development.
The interdisciplinary across of psychology, neurophysi-
ology and machine learning theory promoted the produc-
tion and development of autonomous learning theory and
method directly.
Related researches of neurophysiological theories indi-
cate that, during the sensorimotor learning, the cerebral
cortex, basal ganglia, and cerebellum work in parallel
and unique way [1-3]. The ballpark behavior adapt to the
environment can be learnt through the basal ganglia loop
by reinforcement learning [4], and the ballpark behavior
can be refined by supervised learning in the cerebellum
[5]. Cerebral cortex, utilizing unsupervised Hebbian
learning [6-7], driven by input from basal ganglia and
cerebellum, learns through practice to perform these op-
erations fast and accurately. Studies show that the basal
ganglia are the medium of behavior selection, and nu-
cleus in basal ganglia, such as striatum, globus pallidus,
substantia nigra, et al., play the role of action se- lection
[8-11]. Bernard W. Balleine, et al, from psychology and
brain research institute, university of California, has
studied the integrative function of basal ganglia in oper-
ant learning [12], which indicates that the dorsal striatum
in basal ganglia plays an important role in the operant
conditioning learning process. From above introductions,
it can be seen that human brain is a complex system, and
the basal ganglia and cerebellum in the central nervous
system all play an important role in motor learning. For
motor learning, two different mechanisms can operate to
make use of sensory information to correct motor errors.
The fist is on-line error correction, and the second is
trial-to-trial learning, in the latter case, errors from one

X. G. RUAN ET AL. 215
trial influence the motor output on the next trial. The two
learning mechanisms are related with the cerebellum and
basal ganglia.
However, the motor control and learning mechanism
of cerebellum and basal ganglia seems be studied sepa-
rately. For example, the cerebellum works as an adaptive
filter [13,14] and the feedback error learning in cerebel-
lum is proposed by Kawato [15,16]. An important class
of BG model is known as Actor-Critic models or
RL-based models [17,18] with system-level. In 2008, a
contracting basal ganglia model was proposed for the
action selection mechanism [19]. Although Doya [20]
pointed the complementary roles of cerebellum and basal
ganglia, how to implement such cooperation is not very
specific. This paper is dedicated to the coordinated
learning mechanism between cerebellum and basal gan-
glia.
In the aspect of learning control theory, professor
Wang proposed a kind of hybrid algorithm aiming at the
obstacle avoidance problem of robot [21]. They proposed
a neural fuzzy system with mixed coarse learning and
fine learning phases. In the first phase, supervised learn-
ing method is used to determine the membership func-
tions for the input and output variables simultaneously.
After sufficient training, fine learning is applied which
employs reinforcement learning algorithm to fine tune
the membership. Meng Joo Er et al. also applied hybrid
learning approach for the obstacle avoidance [22]. In the
simulation environment, preliminary supervised learning
was executed applying dynamic fuzzy neural net- works,
and in the real robot, neuro-fuzzy controller is capable of
re-adapting in a new environment. After carrying out the
learning phase on a simulated robot, the controller is
implemented on a real robot. The hybrid learning method
shows the coordination between supervised learning and
reinforcement learning.
In the aspect of learning algorithm research, Michael
et al. combined supervised learning with actor-critic
learning and proposed a supervised learning combined
with an actor-critic architecture [23]. This type of learn-
ing has been suggested by Clouse and Benbrahim [24,25].
In this paper, the supervised actor-critic algorithm is as-
sociated with the interactions between the cerebellum
and basal ganglia. At the same time, operant learning
will be considered in the design of motor learning system
as the action selection mechanism in the basal ganglia.
The example of motor learning in a self-balancing robot
will be present to show the benefits of using the pro-
posed motor learning method.
There are many kinds of two-wheeled self-balancing
robot, such as wheeled-inverted pendulum, self-balanc-
ing wheelchair, JOE, nBot [26-29], and so on. All of
them have ability of keeping balanced themselves and
running forward. For the balancing control, researchers
have done a lot of works for such kinds a robot. An
adaptive output recurrent cerebellar model articulation
controller is utilized to control wheeled inverted pendu-
lums (WIPs) [30]. Grasser et al. [28] developed a dy-
namic model for designing a mobile inverted pendulum
controller using a Newtonian approach and linearization
method. In [26], a dynamic model of a WIP was created
with wheel motor torques as input, accounting for non-
holonomic no-slip constraints. Vehicle pitch and position
were stabilized using two controllers. Jung and Kim [31]
created a mobile inverted pendulum using neural net-
work (NN) control combined with a proportional-inte-
gral-derivative controller. But there are fewer reports for
the autonomous learning based on the neuro-physiologi-
cal theory. Balancing skill’s acquisition is the results of
central nervous system. How to imitate the brain function
and construct a motor learning method for balancing
robot is the main target in this paper.
This paper is organized as follows. Section 2 addresses
the motor learning in the central nervous system of hu-
man being and shows the important role of the cerebel-
lum and basal ganglia in CNS. Section 3 introduces op-
erant learning method. That is an important working
style in the motor learning and it is closely related with
the mechanism of the basal ganglia. Section 4 is the main
part of this paper. Motor learning method with the in-
teraction of the cerebellum and basal ganglia is proposed.
Evaluation mechanism, action selection mechanism and
tropism mechanism are included. The convergence analy-
sis is deduced in the sense of entropy. At last, in section
5, the control structure is designed with the proposed
method for a self-balancing two-wheeled robot and the
comparative experiments are conducted to show the ef-
fectiveness of proposed method. Section 6 concludes.
2. Motor Learning in CNS
An important feature of the central nervous system (CNS)
in its control of movement is the capability of motor
learning. Motor learning is the process of improving the
motor skills, the smoothness and accuracy of movements.
It is important for calibrating simple movements like
reflexes, as parameters of the body and environment
change over time. As we know, for higher mammals,
especially humans, both of supervised learning and rein-
forcement learning are probably the most important class
of motor learning. In the CNS, two auxiliary monitor
systems are the cerebellum and ganglion nuclear group
in the forebrain area. Cerebral cortex, cerebellum and
basal ganglia, cooperated with each other, form complex
motor control system. Figure 1 shows their relations in
CNS [32]. Cerebellum specialize in supervised learning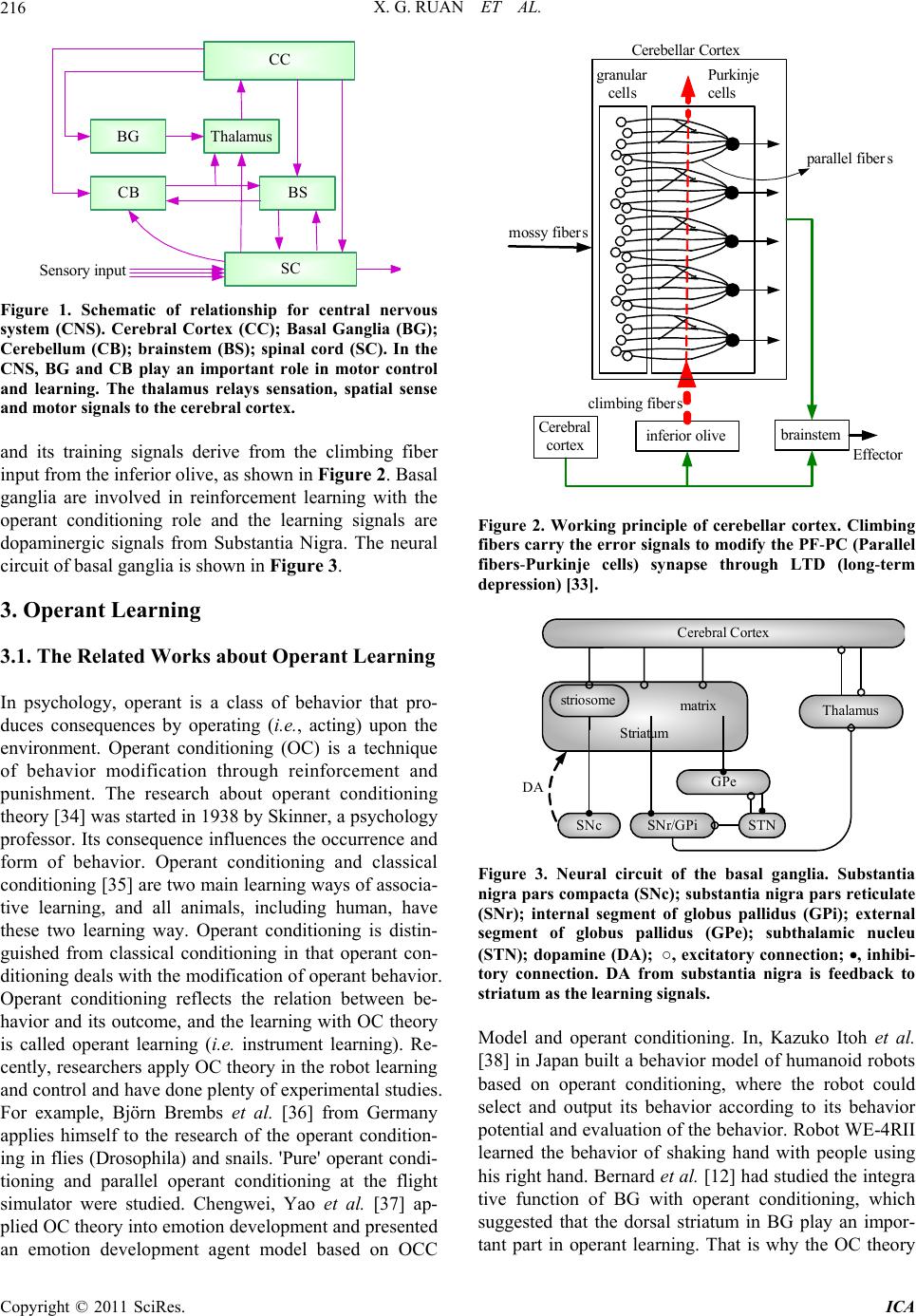

X. G. RUAN ET AL. 216
CC
ThalamusBG
CB BS
SC
Sensory input
Figure 1. Schematic of relationship for central nervous
system (CNS). Cerebral Cortex (CC); Basal Ganglia (BG);
Cerebellum (CB); brainstem (BS); spinal cord (SC). In the
CNS, BG and CB play an important role in motor control
and learning. The thalamus relays sensation, spatial sense
and motor signals to the cerebral cortex.
and its training signals derive from the climbing fiber
input from the inferior olive, as shown in Figure 2. Basal
ganglia are involved in reinforcement learning with the
operant conditioning role and the learning signals are
dopaminergic signals from Substantia Nigra. The neural
circuit of basal ganglia is shown in Figure 3.
3. Operant Learning
3.1. The Related Works about Operant Learning
In psychology, operant is a class of behavior that pro-
duces consequences by operating (i.e., acting) upon the
environment. Operant conditioning (OC) is a technique
of behavior modification through reinforcement and
punishment. The research about operant conditioning
theory [34] was started in 1938 by Skinner, a psychology
professor. Its consequence influences the occurrence and
form of behavior. Operant conditioning and classical
conditioning [35] are two main learning ways of associa-
tive learning, and all animals, including human, have
these two learning way. Operant conditioning is distin-
guished from classical conditioning in that operant con-
ditioning deals with the modification of operant behavior.
Operant conditioning reflects the relation between be-
havior and its outcome, and the learning with OC theory
is called operant learning (i.e. instrument learning). Re-
cently, researchers apply OC theory in the robot learning
and control and have done plenty of experimental studies.
For example, Björn Brembs et al. [36] from Germany
applies himself to the research of the operant condition-
ing in flies (Drosophila) and snails. 'Pure' operant condi-
tioning and parallel operant conditioning at the flight
simulator were studied. Chengwei, Yao et al. [37] ap-
plied OC theory into emotion development and presented
an emotion development agent model based on OCC
inferior olive
granular
cells
Purkinje
cells
mossy fibers
Cerebellar Cortex
climbing fibers
brainstem
Effecto
r
Cerebral
cortex
parallel fibers
Figure 2. Working principle of cerebellar cortex. Climbing
fibers carry the error signals to modify the PF-PC (Parallel
fibers-Purkinje cells) synapse through LTD (long-term
depression) [33].
Cerebral Cortex
Striatum
striosome matrix
SNc SN r/GPi
Thalamus
STN
GPe
DA
Figure 3. Neural circuit of the basal ganglia. Substantia
nigra pars compacta (SNc); substantia nigra pars reticulate
(SNr); internal segment of globus pallidus (GPi); external
segment of globus pallidus (GPe); subthalamic nucleu
(STN); dopamine (DA); ○, excitatory connection; , inhibi-
tory connection. DA from substantia nigra is feedback to
striatum as the learning signals.
Model and operant conditioning. In, Kazuko Itoh et al.
[38] in Japan built a behavior model of humanoid robots
based on operant conditioning, where the robot could
select and output its behavior according to its behavior
potential and evaluation of the behavior. Robot WE-4RII
learned the behavior of shaking hand with people using
his right hand. Bernard et al. [12] had studied the integra
tive function of BG with operant conditioning, which
suggested that the dorsal striatum in BG play an impor-
tant part in operant learning. That is why the OC theory

X. G. RUAN ET AL. 217
is considered in the research of BG mechanism. The
principle of OC is present in the following section.
3.2. The Principle of Operant Conditioning
Theory
Operant conditioning emphasizes that behavior's con-
sequence influences the occurrence. The difference be-
tween operant learning and supervised learning depends
on the feedback signal obtained from environment,
which is valuation signal or error signal. There are three
main elements about the learning control based on OC
theory, including probabilistic action selection mecha-
nism, evaluation mechanism and tropism mechanism,
which is the main part of learning and is used to update
the action selection policy. Figure 4 shows the learning
control mechanism based on OC theory. The probabilis-
tic action selection mechanism is the main part of OC
learning.
4. CB-BG-Based Motor Learning Scheme
4.1. CB-BG-Based Motor Learning Control
Structure
According to the working modes of the cerebellum and
basal ganglia, a CB-BG-based motor learning scheme is
presented, which exploits supervised ac- tor-critic learn-
ing structure, as shown in Figure 5.
The coordinated factor

is used to calculate the
combined action a, which can be got through the fol-
lowing formula.


1
E
S
aa a   (1)
Thereinto,
E
a, the exploratory action, can be got by
an artificial neural networks addition to a probabilistic
action selection mechanism.S a, the supervised action,
can be got by the traditional feedback controller, which
provides intention and solution for the action networks.
a, a simple weighted sum of the actions given by the
component policies, is sent to the environment.
4.2. Algorithm Description
1) Evaluation Networks with BG mechanism: The
evaluation function

Vs can be updated with TD er-
ror[39]:
   
1tt
trt VsVs 

 . t z is the eligi-
bil- ity trace of evaluation networks weights, which is
com- puted by the linear differential equation, defined as,

1
t
tt
t
Vs
zz W 



 (2)
The updating equation of evaluation networks based
()tu ()tX
(+1)
(, (t))
t
ru
XX
Figure 4. Learning control mechanism based on OC theory.
Supervisor
Environment
Combined
Action
Coordinated
factor
State s
Rewarded signal r
Evaluation Mechanism
AN
S
a
E
a
a



IO
BG CB
SN
Probabilistic
Action
Selection
A
a
Tropism
Mechanism
BG
CF

S
e
Figure 5. CB-BG-based motor learning control structure.
BG: Basal Ganglia；CB: Cerebellum; IO: Inferior Olive; SN:
Substantia Nigra; CF: Climbing Fibre; AN: Action
Net-works, which is constituted with the interaction of BG
and CB; Evaluation Mechanism owns to BG. The real line
is the data flow, while the dashed line part is the learning
updating algorithm. Dopaminergic signal (δ) coming from
SN and feedback to striatum in BG is the learning signal for
the action network in BG part. Another learning signal is
the supervised error S
e coming from the Inferior Olive
(IO) in correspondence with the learning mechanism of the
cerebellum. The two parts of learning signals can be
coordinated by coordinated factor

Probabilistic Action
Selection (PAS) mechanism expresses the operant learning
in BG.
E
a, the exploratory action; S a, the supervised
action; r represent the reward signal after executing the
combined action; state s represent the input of action
networks and evaluation networks.
on eligibility trace is that




t
tttz  ww (3)
0

 is a positive constant and express the learning
step of evaluation networks; 01

 is the discount
factor of reward; 01


 is the decay factor of eligi-
bility trace. If


0t   (i.e., the state is better than ex-
pect), the estimated critic value

Vs would be in-
creased. In the contrast, if

0t   (i.e., it is worse
than expect), the estimated value

Vs in the state
would be decreased.

X. G. RUAN ET AL. 218
2) Action Networks with the interaction of CB and BG:
In Figure 5, the actor policy

πA
s
is a mapping from
state to actor and can be given by a function approxima-
tor with the parameter vector

.


π,
AA
as

 (4)
The random action selective strategy
E
a obeys a
probabilistic distribution of Boltzmann-Gibbs [40].
 
1exp E
E
B
a
a
Z
KT








(5)
Thereinto,

2,0
EEA
aaaT    is the thermo-
dynamics temperature, 23 1.3810Js K
B
K  is the
Boltzmann constant,



exp EB aKT   is Boltzmann
factor,
Z
is the partition function, and that:

expd π
E
EB
B
a
Z
aKT
KT
 


 


 (6)
After each state transition, those parameters are modi-
fied according to the following rule. It includes two parts,
CB

 is realized through the function of cerebellum,
and BG

 is correspondence with the basal ganglia
part.

BG CB
1

    (7)
In order to compute the supervised learning update:
CB

, the supervisory error can be defined for each ob-
served state as follows.
 
2 1ππ
2SA
Ess s

(8)
The weights updating of the action networks in cere-
bellum part is that：




CB π
SA A
Esa as

    (9)
The actor networks updating in BG part applies a kind
of approximated policy gradient estimation algorithm:

BG π
EA A
aa s

  (10)
0

 is the learning step of action networks;
01

 weighs between two kinds of gradient infor-
mation, one is related with second evaluation signal

(also called internal return) and another gradient infor-
mation is related with the supervised error

SA
aa. In
order to express the importance of rewarded signal, in-
ternal return signal is introduced into the item
 
CB π
SA A
aa s

  , so we get the improved
weights updating method.


 
π
ES SAA
aa aas


   

(11)
The improved supervised actor networks weight-up-
dating algorithm shows that the TD error modulates the
supervisory error

SA
aa. That is to say, one ‘trusts’
the critic more than the supervisor, in which case one
should view the supervisor as an additional source of
exploration. That is the coordination between the cere-
bellum and basal ganglia. When the internal return

is
small, the actor network loses the ability of learning
through the supervisor. While in the unimproved algo-
rithm, this learning ability only depends on the change of
coordinated factor ω.
3) Tropism Mechanism: In [41], the temperature
parameter defined by the state values and the frequency
of visiting states are added to representative state-action.
By this thought, the probabilistic tropism can be changed
through the temperature T, which depends on the critic
value


Vs. The bigger is the estimated value


Vs,
the better the action tropism is, and the temperature is
more smaller, and vice versa. The smaller


Vs, the
worse tropism, the higher temperature, and system is in
much more stochastic situation. The tropism rule is:


1
2
1exp t
k
TkV s  (12)
Thereinto, 12
0, 0kk, are constant and 1 k is de-
fined as Simulated Annealing factor(SAF), which can
be changed with learning;


t
Vs is the critic value of
current state.
4) Interaction Mechanism of the cerebellum and basal
ganglia: The coordinated factor

expresses the wei-
ght of cerebellum supervisory learning in the whole
learning process. It can be changeable and reflect the role
of cerebellum and basal ganglia in different motor learn-
ing stages. The following exponential increase method
can be used as in literature [42] shown in Figure 6.

2
23
3
max 0,1exp,0
tn nn C
n






 
 



(13)
5) CB-BG-based Motor Learning Algorithm with the
RBF Networks: A radial basis function (RBF) network,
which is an artificial neural network that uses radial basis
functions as activation functions, is proposed by J.
Moody and C. Darken in the late 1980s. It is a linear
combination of radial basis functions. RBF networks
imitate the neural networks structure of local adjustment
and mutual covered receptive fields in human brain. The
0500 1000 15002000 2500 3000
0
0.2
0.4
0.6
0.8
1
t/s
Exponential increase
ω
0500 1000 15002000 2500 3000
0
0.2
0.4
0.6
0.8
1
t/s
Exponential increase
ω
Figure 6. CB coordination factor.

X. G. RUAN ET AL. 219
radial basis function can be used for the coding of
CMAC. The conventional CMAC uses constant binary
or triangular receptive-field basis function. However, the
derivative information is not preserved. To acquire de-
rivative information of input and output variable, Chiang
and Lin developed a CMAC with a differentiable Gaus-
sian receptive-field basis function and provided conver-
gence analysis results for this network [43]. As men-
tioned above, we will approximate action and evaluation
functions by RBF neural networks in our proposed algo-
rithm.
The three layers topological structure of RBF net-
works is shown in Figure 7, which is introduced in detail
as follows.
 The first is the input layer, which is for input space.
Each neuron is corresponding to an input variable,
and given that

T
12
,,, n
n
xx xx.
 The second is the hidden layer, in which every node
is a Gaussian function. The vector formed by output
of hidden layer,

B
T
12
,,,
n
    , B n is called
the resolution. The bigger B
n has a higher resolu-
tion.

2
2
1
exp 2
nkki
i
kki
xc
b








 (14)
where,

T
12
,,, n
iii ni
cc cc is the center vector;


T
12 B
,,,, 1,2,,
n
iii ni
bb binbis the base
width vector.
 The third is the output layer, which have one node,
used for approximating the unknown nonlinear func-
tion. The weights vector is: B
T
12
,,,
n
vv v

 v, and
the output is got.
B
out
1
n
T
ii
i
yv




v  (15)
For the action and evaluation networks, the same
structure of RBF neural networks is used. The output
weights vector of actor and evaluation networks are rep-
State
2
2
1
()
exp[ ]
2
n
kki
i
kki
xc
b





1
v
2
v
3
v
B
n
v
out
y
(,)
ki ki
cb
1
()
x
t
()
i
x
t
()
n
x
t
Figure 7. Architecture of a RBFN.
resented with

and w respectively. So the process
of CB-BG-based motor learning algorithm with the RBF
networks can be concluded as follows:
CB-BG-based Motor Learning Algorithm:
Step 1: Initialization: Initiate the learning step α, β;
discount factor


0, 1  ; eligibility trace delay factor


0, 1  ; Initiate arbitrarily all weights parameters

and w; Let 0trytime

.
Step 2: Repeat (for each episode):
1) t←0；z0←0 (reinitialize eligibility trace), Choose
an initial state 0
s
.
2) Repeat (for each step in the episode):
a) For current state t
s
, calculate


π
AAt
as;


π
SSt
as; Select exploration action
E
a ac-
cording to Boltzmann distribution; set the coor-
dinated factor

; compute the combined action
a and the eligibility trace


1tt t
zz s 

  .
b) Execute action a, receive immediate reward


rt,
then observe the new state 1t
s
; calculate TD er-
ror



 
1tt
trt Vss 

 ; update the
weights through
 

1t tt
tz 
ww ; until
satisfied the condition




1,tt

 ww ;
 




1
E
SSAt
tt aa aas
 

 

 
c) 1tt

;
Until the desired number of episodes has been investi-
gated.
4.2. Algorithm Convergence Analyses
Theorem 1: Action
E
a obeys probability distribution
of Boltzmann-Gibbs:
 
1exp E
E
B
a
a
Z
KT






, where,

2
EEA
aaa   ,


expd π
E
EB
B
a
Z
aKT
KT
 


 


， The sum of the
probability in real sets is one.
Proof: The sum of the probability in real sets can be
compute in the following integral equation.
 

1
dexp d
π
1exp d1
ππ
E
p
EE E
B
EB
E
B
BB
a
aa a
ZKT
aKT
a
KT
KT KT



 
 



 









Theorem 2: Along with learning, the entropy of sys-
tem:
  
2
log d
E
EE
Ea aa 



 decreases grad-
ually, and system changes from uncertainty to certainty
as time.
Proof: The sum of the probability in real sets can be
compute in the following integral equation.

X. G. RUAN ET AL. 220
Literature [44] listed several entropy of continuous
probability distribution, and the entropy of continuous
system with obeys normal distribution is:

2
2
1log 2π
2
Ee

. It can be got that the probability
distribution of Boltzmann-Gibbs in the paper is consis-
tent with normal distribution: ,2
B
S
K
T
Na




, that is to
say, the mean is S a

 and the variance
2
2
B
K
T Z
  .
So that, the entropy of the continuous system is:

2
1log π
2B
EeKT (16)
Along with the learning progress,

Vs approxi-
mates the largest sum of discounted reward. According
to the tropism mechanism as formula (12), and by setting
suitable parameters, the explore and exploit can keep
coordinated, and the action policy which has been learnt
at last can satisfy

ππ
πarg maxEE
EVs
. The learning
algorithm makes the function

Vs developing toward
the maximum direction. From the tropism mechanism,
we can find that T would decrease with the increase of V.
The system transforms from uncertainty to certainty
along with learning.
Entropy of discrete system has better characters, such
as, non-negative characteristic and coordinates transfor-
mation invariability, etc. Different with discrete system,
entropy of continuous system, also called cross-entropy
or differential entropy, does not have characteristics
above. When
 
21
1π8.485510K ,
B
TeK 0E

,
the entropy could be negative as shown in Figure 8.
Therefore, the proposed method is convergence in the
sense of entropy, and the system changes from uncer-
tainty to certainty.
5. Simulation Experiment and Analyses
5.1. Self-Balancing Two-Wheeled Robot
Self-balancing two-wheeled robot is a complex nonlinear
under-actuated system and has self-balancing skill like
human. There is important theory signification to re-
search about the cognition mode of robot. The schematic
structure is shown in Figure 9.
Parameters are defined in Table 1 which is shown in
Appendix.
The dynamic mathematic model is



,
M
qq NqqET
 
  (17)
where,

T
,,
bl r
q   ,

T21
lr
T 

, the ma-
00.5 11.5 2
x 1023
-2
-
1
0
1
2
3
T/K
Entropy / (bit)
(1/(eKB), 0)
E>0
E<0
00.5 11.5 2
x 1023
-2
-
1
0
1
2
3
T/K
Entropy / (bit)
(1/(eKB), 0)
E>0
E<0
Figure 8. Entropy changing with temperature T.
l

r

b

Figure 9. System structure of robot.
Table 1. Definition of Parameters.
Parameter Description Value
,
lr
mm kg mass of the left and the right
wheel 1
M/kg the mass of the intermediate
body 10
R/m radius of wheel 0.15
d/m distance between the 01 and 0r 0.44
L/m distance between the 0 and G 0.4
Jl = Jr = Jw/kg·m2 the moment of inertia of (left
and right wheel) about its axis 0.01125
Jy/kg·m2 the moment of inertia of the
robot about the y –axis 1.5417
Jz/kg·m2 the moment of inertia about the
z –axis 0.5893
g/m/s2 acceleration of gravity 9.8
,
lr

 /(N·m/(rad/s)) frictional coefficient of two
wheels with ground 0.1,0.1
w

/(N·m/(rad/s)) frictional coefficient of the
wheels axis 0.1
x/m forward displacement of robot variable
v/(m/s) forward velocity of robot variable
b

/rad inclination angle of the inter-
mediate body variable
b

/ rad/s inclination angle velocity of the
intermediate body variable
,radrads 
 yaw angle and angle velocity of
robot variable
,
rl

 /rad rotary angle of the right and left
wheel variable
,
lr

 / rad/s rotary angle velocity of the
right and left wheel variable
l

/N.m torque provided by left motor [–5, 5]
r

/N.m torque provided by right motor [–5, 5]

X. G. RUAN ET AL. 221
trix is illustrated in appendix.
According to the definition of under-actuated system,
the affined nonlinear system can be formulated with

12
,, ,,qfqqtfqqt u
 
 
, and if the following condi-
tion is satisfied:


2, ,dimrankfq q tq




  (i.e. the
number of actuators is less than DOF, degree of free-
dom)，the system is an under-actuated system. As for the
two-wheeled self-balancing robot,

123rankMq E 



, so that it is an under-actuated
system. Equation (16) is left multiplied transformation
matrix A,


,
A
Mqq ANqqAET
 
 , where,
111
010
001
A





. Then we can get:



,qqqq ET

 
 
  (18)
where,
T
010
001
EAE




Equation (18) can be divided into:


11 11221
21 12222
,0
,
qq qq
qq qq 
 

 


 
 
 
 
(19)
where, 12
,, ,
nl m
qq qlnm
 , 1
q
 denote
all the passive joints, and 2 q
 denote the actuated joints;
 denotes the Coriolis force and gravity terms.

11 12
21 22
q





, where

is positive definite,
11
 and 22  are also positive definite. Through the
controllability analysis, we can conclude that the system
is controllable. So it is important that under-actuated
system is not necessarily an uncontrollable system.
5.2. Simulation Experiment
Applying the motor learning method proposed in Section
IV, we did a simulation research on a self-balancing
two-wheeled robot for the balance skill learning, and the
bionic learning control structure is illustrated in Figure
10. There are mainly five parts in the control system:
receptor, afferent nerve, nerve centre, efferent nerve and
effector. The proposed CB-BG-based motor learning
method in Section 4 is included in the nerve centre. DAS
denotes data acquisition system.
According to the sliding mode control thought, we
define the rewarded function and the sliding surface H as
follows:

 
:0Hxsx (20)


12bb
s
ta tat  
 (21)
We can obtain the reward information according to
the changing of the sliding surface. After executing an
action, if


s
t changes near to zero, give it reward.
Conversely, give it penalty. 0 denotes reward, and -1
denotes penalty. It can be formulated as:
 
22
0(reward) if1
1(penalty)else
t
st st
r



 (22)
Detect the robot states signals, and normalize the input
signals which are sent to the CNS including the cerebel-
lum and basal ganglia. The coordinated factor

is
used in the form of exponential decay as formula (13).
The parameters are chosen as follows.
s
Tis the sampling
time. ,
bb
nn


 are the normalizing factor for angle and
angle velocity separately.


12
231
2
T
12
T
12
49 1491
10; 2; 49; 10; 0.1; 0.1;
0.1; 0.8; 0.8; 500; 200; 10;
1; π54; π54;
3,2, 1,0,1,2,3;
0.5,0.5,0.5,0.5,0.5,0.5,0.5
;;;
5
bb
sB
acll
S
Tmsnnk k
nna
an n
cc
bb
wRwR a
a






  
 
 


 


w 

0102 2
bb llll
  

The initial inclination angle



00.1744
brad
 .
1) The first experiment: two experiments are done for
contrast. One with cerebellum coordinated, and another
without cerebellum coordinated. Observe the result of
inclination angle b

.
Enco-
der
DAS
DFS
(data fusion system)
Left
wheel
Gyro Incli-
nator
Body
posture
Enco-
der
Right
wheel
bb llrr

  

Robot
Motor servo module
D/A
Converter
Cere b e llu m
Basal Ganglia
CB-BG-based Motor
learning method
RECEPTORAFFERENT NERVENERVE CENTRE
EFFERENT
NE RVE
EFFECTOR
Robot States
,
lr


Figure 10. The bionic motor learning structure for self-
balancing two-wheeled robot.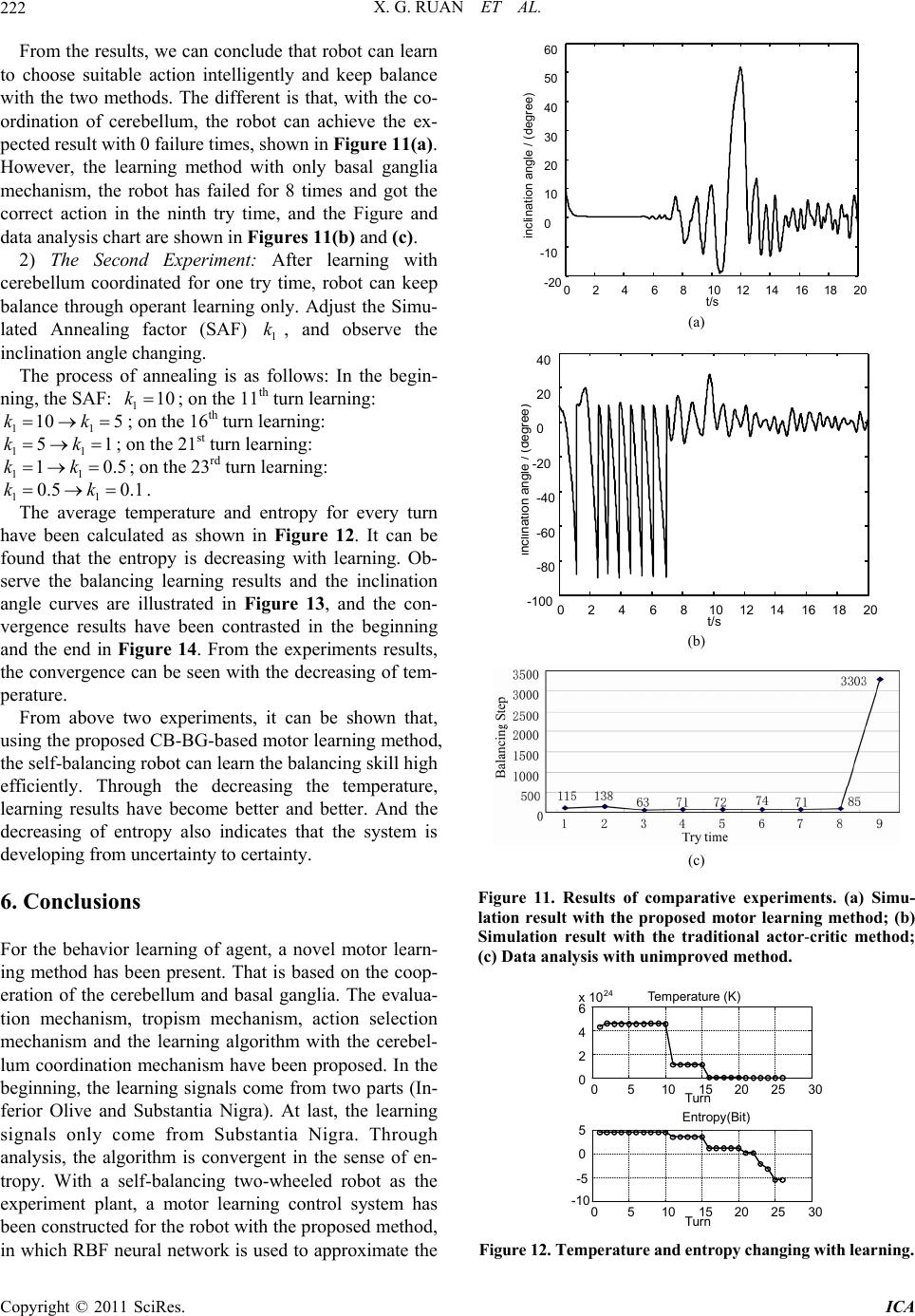

X. G. RUAN ET AL. 222
From the results, we can conclude that robot can learn
to choose suitable action intelligently and keep balance
with the two methods. The different is that, with the co-
ordination of cerebellum, the robot can achieve the ex-
pected result with 0 failure times, shown in Figure 11(a).
However, the learning method with only basal ganglia
mechanism, the robot has failed for 8 times and got the
correct action in the ninth try time, and the Figure and
data analysis chart are shown in Figures 11(b) and (c).
2) The Second Experiment: After learning with
cerebellum coordinated for one try time, robot can keep
balance through operant learning only. Adjust the Simu-
lated Annealing factor (SAF) 1 k, and observe the
inclination angle changing.
The process of annealing is as follows: In the begin-
ning, the SAF: 110k; on the 11th turn learning:
11
10 5kk; on the 16th turn learning:
11
51kk ; on the 21st turn learning:
11
10.5kk ; on the 23rd turn learning:
11
0.5 0.1kk.
The average temperature and entropy for every turn
have been calculated as shown in Figure 12. It can be
found that the entropy is decreasing with learning. Ob-
serve the balancing learning results and the inclination
angle curves are illustrated in Figure 13, and the con-
vergence results have been contrasted in the beginning
and the end in Figure 14. From the experiments results,
the convergence can be seen with the decreasing of tem-
perature.
From above two experiments, it can be shown that,
using the proposed CB-BG-based motor learning method,
the self-balancing robot can learn the balancing skill high
efficiently. Through the decreasing the temperature,
learning results have become better and better. And the
decreasing of entropy also indicates that the system is
developing from uncertainty to certainty.
6. Conclusions
For the behavior learning of agent, a novel motor learn-
ing method has been present. That is based on the coop-
eration of the cerebellum and basal ganglia. The evalua-
tion mechanism, tropism mechanism, action selection
mechanism and the learning algorithm with the cerebel-
lum coordination mechanism have been proposed. In the
beginning, the learning signals come from two parts (In-
ferior Olive and Substantia Nigra). At last, the learning
signals only come from Substantia Nigra. Through
analysis, the algorithm is convergent in the sense of en-
tropy. With a self-balancing two-wheeled robot as the
experiment plant, a motor learning control system has
been constructed for the robot with the proposed method,
in which RBF neural network is used to approximate the
0 2 46 810 12 14 16 18 20
-20
-10
0
10
20
30
40
50
60
t/s
incli nati on angl e / (deg re e)
(a)
0 2 4 6 810 12 14 16 18 20
-100
-80
-60
-40
-20
0
20
40
t/s
i
nc
li
na
ti
on ang
l
e
/
(d
egree
)
(b)
(c)
Figure 11. Results of comparative experiments. (a) Simu-
lation result with the proposed motor learning method; (b)
Simulation result with the traditional actor-critic method;
(c) Data analysis with unimproved method.
05 1015 20 25 30
0
2
4
6
Turn
Entropy ( Bi t )
5
0
-5
Temperat ure (K)
05 1015 20 25 30
-10
Turn
24
x 10
Figure 12. Temperature and entropy changing with learning.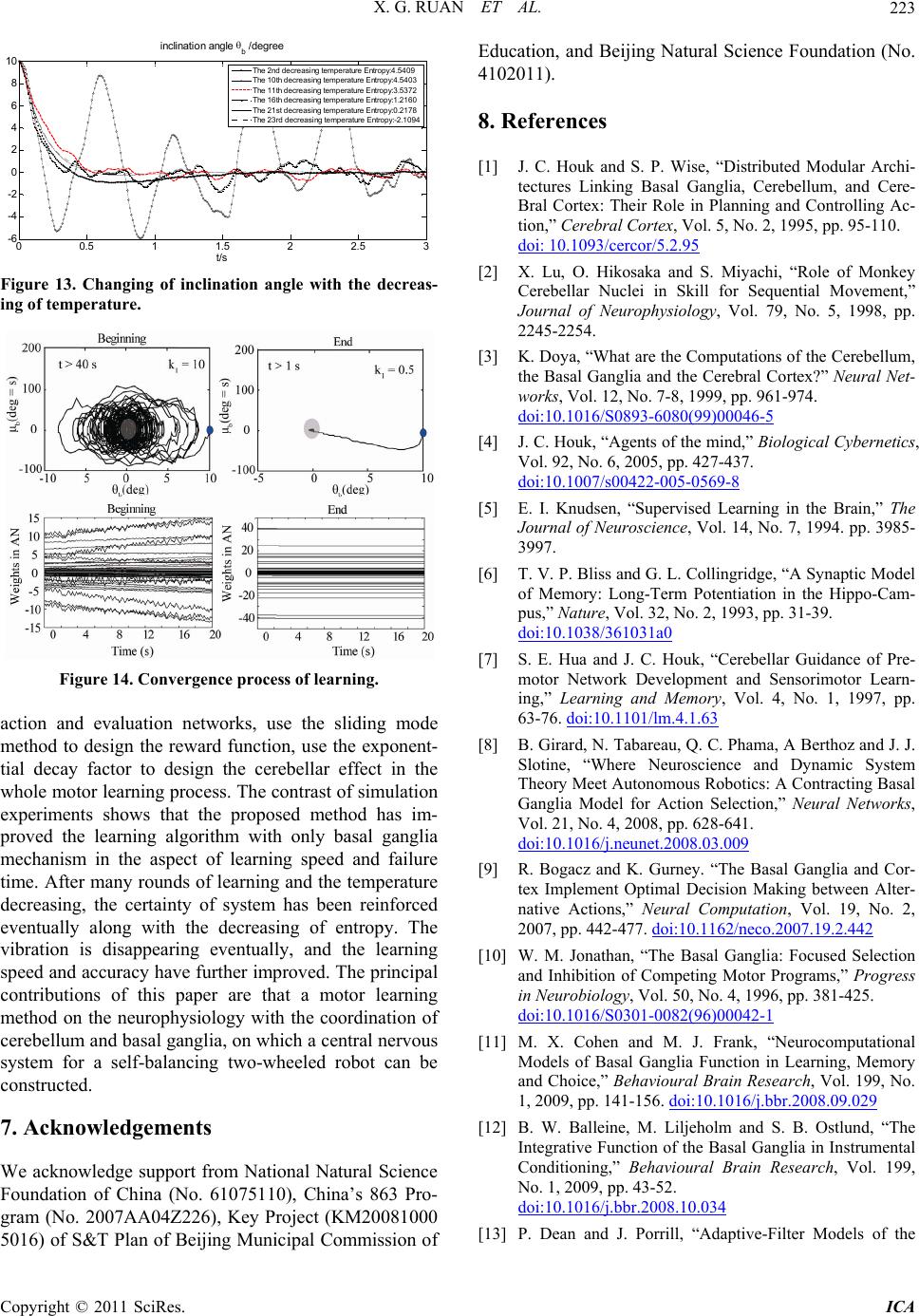

X. G. RUAN ET AL. 223
00.511.5 22.5 3
-6
-4
-2
0
2
4
6
8
10
t/s
inclination angle

b
/degree
The 2nd decr easin g t em per at ur e Entr opy: 4.5409
The 10t h decr easin g t em per at ur e Ent r opy: 4. 5403
The 11t h decr easin g t em per at ur e Ent r opy: 3. 5372
The 16t h decr easin g t em per at ur e Ent r opy: 1. 2160
The 21st decr easin g temper at ur e Entr opy: 0.2178
The 23r d decr easin g t em per at ur e Entropy:- 2.1094
Figure 13. Changing of inclination angle with the decreas-
ing of temperature.
Figure 14. Convergence process of learning.
action and evaluation networks, use the sliding mode
method to design the reward function, use the exponent-
tial decay factor to design the cerebellar effect in the
whole motor learning process. The contrast of simulation
experiments shows that the proposed method has im-
proved the learning algorithm with only basal ganglia
mechanism in the aspect of learning speed and failure
time. After many rounds of learning and the temperature
decreasing, the certainty of system has been reinforced
eventually along with the decreasing of entropy. The
vibration is disappearing eventually, and the learning
speed and accuracy have further improved. The principal
contributions of this paper are that a motor learning
method on the neurophysiology with the coordination of
cerebellum and basal ganglia, on which a central nervous
system for a self-balancing two-wheeled robot can be
constructed.
7. Acknowledgements
We acknowledge support from National Natural Science
Foundation of China (No. 61075110), China’s 863 Pro-
gram (No. 2007AA04Z226), Key Project (KM20081000
5016) of S&T Plan of Beijing Municipal Commission of
Education, and Beijing Natural Science Foundation (No.
4102011).
8. References
[1] J. C. Houk and S. P. Wise, “Distributed Modular Archi-
tectures Linking Basal Ganglia, Cerebellum, and Cere-
Bral Cortex: Their Role in Planning and Controlling Ac-
tion,” Cerebral Cortex, Vol. 5, No. 2, 1995, pp. 95-110.
doi: 10.1093/cercor/5.2.95
[2] X. Lu, O. Hikosaka and S. Miyachi, “Role of Monkey
Cerebellar Nuclei in Skill for Sequential Movement,”
Journal of Neurophysiology, Vol. 79, No. 5, 1998, pp.
2245-2254.
[3] K. Doya, “What are the Computations of the Cerebellum,
the Basal Ganglia and the Cerebral Cortex?” Neural Net-
works, Vol. 12, No. 7-8, 1999, pp. 961-974.
doi:10.1016/S0893-6080(99)00046-5
[4] J. C. Houk, “Agents of the mind,” Biological Cybernetics,
Vol. 92, No. 6, 2005, pp. 427-437.
doi:10.1007/s00422-005-0569-8
[5] E. I. Knudsen, “Supervised Learning in the Brain,” The
Journal of Neuroscience, Vol. 14, No. 7, 1994. pp. 3985-
3997.
[6] T. V. P. Bliss and G. L. Collingridge, “A Synaptic Model
of Memory: Long-Term Potentiation in the Hippo-Cam-
pus,” Nature, Vol. 32, No. 2, 1993, pp. 31-39.
doi:10.1038/361031a0
[7] S. E. Hua and J. C. Houk, “Cerebellar Guidance of Pre-
motor Network Development and Sensorimotor Learn-
ing,” Learning and Memory, Vol. 4, No. 1, 1997, pp.
63-76. doi:10.1101/lm.4.1.63
[8] B. Girard, N. Tabareau, Q. C. Phama, A Berthoz and J. J.
Slotine, “Where Neuroscience and Dynamic System
Theory Meet Autonomous Robotics: A Contracting Basal
Ganglia Model for Action Selection,” Neural Networks,
Vol. 21, No. 4, 2008, pp. 628-641.
doi:10.1016/j.neunet.2008.03.009
[9] R. Bogacz and K. Gurney. “The Basal Ganglia and Cor-
tex Implement Optimal Decision Making between Alter-
native Actions,” Neural Computation, Vol. 19, No. 2,
2007, pp. 442-477. doi:10.1162/neco.2007.19.2.442
[10] W. M. Jonathan, “The Basal Ganglia: Focused Selection
and Inhibition of Competing Motor Programs,” Progress
in Neurobiology, Vol. 50, No. 4, 1996, pp. 381-425.
doi:10.1016/S0301-0082(96)00042-1
[11] M. X. Cohen and M. J. Frank, “Neurocomputational
Models of Basal Ganglia Function in Learning, Memory
and Choice,” Behavioural Brain Research, Vol. 199, No.
1, 2009, pp. 141-156. doi:10.1016/j.bbr.2008.09.029
[12] B. W. Balleine, M. Liljeholm and S. B. Ostlund, “The
Integrative Function of the Basal Ganglia in Instrumental
Conditioning,” Behavioural Brain Research, Vol. 199,
No. 1, 2009, pp. 43-52.
doi:10.1016/j.bbr.2008.10.034
[13] P. Dean and J. Porrill, “Adaptive-Filter Models of the

X. G. RUAN ET AL. 224
Cerebellum: Computational Analysis,” The Cerebellum,
Vol. 7, No. 4, 2008, pp. 567-571.
doi:10.1007/s12311-008-0067-3
[14] P. Dean, J. Porrill, C. F. Ekerot E and J. Henrik, “The
Cerebellar Microcircuit as an Adaptive Filter: Experi-
mental and Computational Evidence,” Nature Reviews
Neuroscience, Vol. 11, No. 1, 2010, pp. 30-43.
doi:10.1038/nrn2756
[15] M. Kawato, “Feedback-Error-Learning Neural Network
for Supervised Motor Learning,” Elsevier, Amsterdam,
1990.
[16] M. Kawato and H. Gomi, “A Computational Model of
Four Regions of the Cerebellum Based on Feeback-Error-
Learning,” Biological Cybernetics, Vol. 68, No, 2, 1992,
pp. 95-103.
doi:10.1007/BF00201431
[17] D. Joel, Y. Niv and E. Ruppin, “Actor-Critic Models of
the Basal Ganglia: New Anatomical and Computational
Perspectives,” Neural Network, Vol. 15, No. 4-6, 2002,
pp. 535-547. doi:10.1016/S0893-6080(02)00047-3
[18] M. Khamassi, L. Lachèze, B. Girard, A. Berthoz and A.
Guillot, “Actor-Critic Models of Reinforcement Learning
in the Basal Ganglia: from Natural to Artificial Rats,”
Adaptive Behavior, Vol. 13, No. 2, 2005, pp. 131-148.
doi:10.1177/105971230501300205
[19] B. Girard, N. Tabareau, Q. C. Phama, A. Berthoz and J. J.
Slotine, “Where Neuroscience and Dynamic System
Theory Meet Autonomous Robotics: A Contracting Basal
Ganglia Model for Action Selection,” Neural Networks,
Vol. 21, No. 4, 2008, pp. 628-641.
doi:10.1016/j.neunet.2008.03.009
[20] K. Doya, “Complementary Roles of Basal Ganglia and
Cerebellum in Learning and Motor Control,” Current
Opinion in Neurobiology, Vol. 10, No. 6, 2000, pp.
732-739. doi:10.1016/S0959-4388(00)00153-7
[21] C. Ye, N. H. C. Yung and D. W. Wang, “A Fuzzy Con-
troller with Supervised Learning Assisted Reinforcement
Learning Algorithm for Obstacle Avoidance,” IEEE
Transactions on Systems, Man, and Cybernetics, Part B:
Cybernetics, Vol. 33, No. 1, 2003, pp. 17-27.
doi:10.1109/TSMCB.2003.808179
[22] M. J. Er and C. Deng, “Obstacle Avoidance of a Mobile
Robot Using Hybrid Learning Approach,” IEEE Trans-
actions on Industrial Electronics, Vol. 52, No. 3, 2005,
pp. 898-905. doi:10.1109/TIE.2005.847576
[23] M. T. Rosenstein and A. G. Barto, “Learning and Ap-
proximate Dynamic Programming: Scaling Up to the
Real World,” IEEE Press and John Wiley & Sons, Inc.,
New York, 2004.
[24] J. A. Clouse and P. E. Utgoff, “A Teaching Method for
Reinforcement Learning,” Proceedings of the Nineth In-
ternational Conference on Machine Learning, San Fran-
cisco, 1992, pp. 92-101.
[25] H. Benbrahim, and J. A. Franklin, “Biped Dynamic
Walking Using Reinforcement Learning,” Robotics and
Autonomous Systems, Vol. 22, No. 3-4, 1997, pp. 283-
302. doi:10.1016/S0921-8890(97)00043-2
[26] K. Pathak, J. Franch and S. K. Agrawal, “Velocity and
Position Control of a Wheeled Inverted Pendulum by
Partial Feedback Linearization,” IEEE Transactions on
Robotics, Vol. 21, No. 3, 2005, pp. 505-513.
doi:10.1109/TRO.2004.840905
[27] A Blankespoor and R Roemer, “Experimental Verifica-
tion of the Dynamic Model for a Quarter Size
Self-Balancing Wheelchair,” Proceedings of the 2004
American Control Conference, Boston, 2004, pp. 488-
492.
[28] F Grasser, A. D’Arrigo, S. Colombi and A. C. Rufer,
“JOE: A Mobile, Inverted Pendulum,” IEEE Transac-
tions on Industrial Electronics, Vol. 49, No. 1, 2002, pp.
107-114. doi:10.1109/41.982254
[29] D. P. Anderson, “NBot Balancing Robot, a Two Wheel
Balancing Robot,” 2003.
http://www.geology.smu.edu/~dpa-ww/robo/nbot/index.
html.
[30] C.-H. Chiu, “The Design and Implementation of a
Wheeled Inverted Pendulum Using an Adaptive Output
Recurrent Cerebellar Model Articulation Controller,”
IEEE Transactions on Industrial Electronics, Vol, 57, No.
5, 2010, pp. 1814-1822. doi:10.1109/TIE.2009.2032203
[31] S. Jung and S. S. Kim, “Control Experiment of a
Wheel-Driven Mobile Inverted Pendulum Using Neural
Network,” IEEE Transactions on Control Systems Tech-
nology, Vol. 16, No. 2, 2008, pp. 297-303.
doi:10.1109/TCST.2007.903396
[32] L. Q. Han and X. Y. Tu, “Study of Artificial Brain Based
on Multi-Centrum Self-Coordination Mechanism,” Sci-
ence Press, Beijing, 2009.
[33] C. Chen and R. F. Thompson, “Temporal Specificity of
Long-Term Depression in Parallel Fiber - Purkinje Syn-
apses in Rat Cerebellar Slice,” Learning and Memmory,
Vol. 2, No. 3-4, 1995, pp. 185-198.
doi:10.1101/lm.2.3-4.185
[34] B. F. Skinner, “The Behavior of Organisms,” Apple-
ton-Century-Crofts, New York, 1938.
[35] I. P. Pavlov, “Conditioned Reflexes,” Oxford University
Press, Oxford, 1927.
[36] B. Brembs, W. Plendl, “Double Dissociation of PKC and
AC Manipulations on Operant and in Drosophila,” Cur-
rent Biology, Vol. 18, No. 15, 2008, pp. 1168-1171.
doi:10.1016/j.cub.2008.07.041
[37] C. W. Yao and G. C. Chen, “A Emotion Development
Agent Model Based on OCC Model and Operant Condi-
tioning,” 2001 International Conferences on Info-Tech
and Info-Net Proceedings, Beijing, 2001, pp. 246-250.
[38] K.Itoh, H. Miwa, M. Matsumoto, M. Zecca, M. Takanobu,
H. Roccella, S. Carrozza, M. C. Dario and P. Takanishi,
“Behavior Model of Humanoid Robots Based on Operant
Conditioning,” Proceedings of 2005 5th IEEE-RAS In-
ternational Conference on Humanoid Robots IEEE/RAS
International Conference on Humanoid Robots, Tsukuba,
2005, pp. 220-225.
[39] J. S. Leng, L. Jain and C. Fyfe, “Convergence Analysis
on Temporal Difference Learning. International Journal

X. G. RUAN ET AL. 225
of Innovative Computing,” Information and Control, Vol.
5, No. 4, 2009, pp. 913-922.
[40] X. G. Ruan, “Neural Computational Science: Simulation
Brain Function at the Cellular Level,” National Defense
Industry Press, Beijing, 2006.
[41] M. Murata and S. Ozawa, “A Reinforcement Learning
Model Using Deterministic State-Action Sequences,” In-
ternational Journal of Innovative Computing, Informa-
tion and Control, Vol. 6, No. 2, 2010, pp. 577-590.
[42] J. Randlov, A. G. Barto and M. T. Rosenstein, “Combin-
ing Reinforcement Learning with a Local Control Algo-
rithm,” Proceedings of the Seventeenth International
Conference on Machine Learning, Vol. 1, No. 4, 2000, pp.
775-782.
[43] C. T. Chiang and C. S. Lin, “CMAC with General Basis
Functions,” Neural Network, Vol. 9, No. 7, 1996, pp.
1199-1211. doi:10.1016/0893-6080(96)00132-3
[44] A. V. Lazo and P. Rathie, “On the Entropy of Continuous
Probability Distributions,” IEEE Transactions on Infor-
mation Theory, Vol. 24, No. 1, 1978, pp. 120-122.
doi:10.1109/TIT.1978.1055832
Appendix
The detail dynamic model of self-balancing two-wheeled
robot is as follows.


,
M
qq NqqET
 
  (17)
where,


11 1213
21 2223
31 3233
1
2
3
;
11
,;10
01
mmm
Mqm m m
mmm
n
Nqqn E
n






 
 

 
 
 




2
11
y
mMLJ
2131 12 13
1cos
2b
mmmm MLR


 
2
2222
22 2
1sin
4
lw bz
R
mm RJMRMLJ
d
  

2
222
23 322
1sin
4bz
R
mm MRMLJ
d
  ;
 
2
2222
33 2
1sin
4
rw bz
R
mmRJMRMLJ
d
  

22
1sinsin cos
2
bbb
wbwlr
nMgL ML



 





2
22
2
1
sin 2sin
2
lrbbbb
lwlwb
R
nMLMLR
d

 





 




;


2
22
3
1
sin 2sin
2
lrbbb b
rwrwb
R
nML MLR
d

 


 


 



