 Intelligent Control and Automation, 2011, 2, 186-195 doi:10.4236/ica.2011.23023 Published Online August 2011 (http://www.SciRP.org/journal/ica) Copyright © 2011 SciRes. ICA An Antilock-Braking Systems (ABS) Control: A Technical Review Ayman A. Aly1,2, El-Shafei Zeidan1,3, Ah me d Hamed1,3, Farhan Salem1 1Department of Mechanical Engineering, Faculty of Engineering, Taif University, Al-Haweiah, Saudi Arabia 2Department of Mechanical Engineering, Faculty of Engineering, Assiut University, Assiut, Egypt 3Department of Mechanical Power Engineering, Faculty of Engineering, Mansoura University, Mansoura, Egypt E-mail: ayman_aly@yahoo.com Received April 23, 2011; revised May 18, 2011; accepted May 25, 2011 Abstract Many different control methods for ABS systems have been developed. These methods differ in their theo- retical basis and performance under the changes of road conditions. The present review is a part of research project entitled “Intelligent Antilock Brake System Design for Road-Surfaces of Saudi Arabia”. In the present paper we review the methods used in the design of ABS systems. We highlight the main difficulties and summarize the more recent developments in their control techniques. Intelligent control systems like fuzzy control can be used in ABS control to emulate the qualitative aspects of human knowledge with several ad- vantages such as robustness, universal approximation theorem and rule-based algorithms. Keywords: ABS, Intelligent Control, Fuzzy Control 1. Introduction Since the development of the first motor driven vehicle in 1769 and the occurrence of first driving accident in 1770, engineers were determined to reduce driving acci- dents and improve the safety of vehicles [1]. It is obvious that efficient design of braking systems is to reduce acci- dents. Vehicle experts have developed this field through the invention of the first mechanical antilock-braking system (ABS) system which have been designed and produced in aerospace industry in 1930 [2,3]. In 1945, the first set of ABS brakes w ere put on a Boeing B-47 to prevent spin outs and tires from blowing and later in the 1950s, ABS brakes were commonly installed in airplanes [4,5]. Soon after, in the 1960s, high end automobiles were fitted with rear-only ABS, and with the rapid progress of microcomputers and electronics tech- nologies, the trend exploded in the 1980s. Today, all- wheel ABS can be found on the majority of late model vehicles and even on select motorcycles [6-10]. ABS is recognized as an important contribution to road safety as it is designed to keep a vehicle steerable and stable during heavy braking moments by preventing wheel lock. It is well known that wheels will slip and lockup during severe braking or when braking on a slip- pery (wet, icy, etc.) road surface. This usually causes a long stopping distance and sometimes the vehicle will lose steering stability [11-13]. Th e objective of ABS is to manipulate the wheel slip so that a maximum friction is obtained and the steering stability (also known as the lateral stability) is maintained. That is, to make th e vehi- cle stop in the shortest distance possible while maintain- ing the directional control. The ideal goal for the control design is to regulate th e wheel v elo city. The techno log ies of ABS are also applied in traction control system (TCS) and vehicle dynamic stability control (VDSC) [14]. Typical ABS components include: vehicle’s physical brakes, wheel speed sensors (up to 4), an electronic con- trol unit (ECU), brake master cylinder, a hydraulic modulator unit with pump and valves as shown in Figure 1. Some of the advanced ABS systems include acceler- ometer to determine the deceleration of the vehicle. This paper is intended to present a literature review of re- search works done by many researchers concerning various aspects of ABS technology in an effort to im- prove the performance of its applications. 2. Principles of Antilock-Brake System The reason for the development of antilock brakes is in essence very simple. Under braking, if one or more of a vehicle’s wheels lock (begins to skid) then this has a  A. A. ALY ET AL.187 Figure 1. Typical ABS components [4]. number of consequences: a) braking distance increases, b) steering control is lost, and c) tire wear will be abnormal. The obvious consequence is that an accident is far more likely to occur. The application of brakes generates a force that impedes a vehicles motion by applying a force in the opposite direction. During severe braking scenarios, a point is obtained in which the tangential velocity of the tire surface and the velocity on road surface are not the same such that an optimal slip which corresponds to the maximum friction is obtained. The ABS controller must deal with the brake dynamics and the wheel dynamics as a whole plant [15]. The wheel slip, S is defined as: VR sV (1) where ω, R, and V de note the wh eel angular v elocity, th e wheel rolling radius, and the vehicle forward velocity, respectively. In normal driving conditions, V = ωR, therefore S = 0. In severe braking, it is common to have ω = 0 while S = 1, which is called wheel lockup. Wheel lockup is undesirable since it prolongs the stopping dis- tance and causes the loss of direction control [16,17]. Figure 2 shows the relationship between braking co- efficient and wheel slip. It is shown that the slide values for stopping/traction force are proportionately higher than the slide values for cornering/steering force. A locked-up wheel provides low road handling force and minimal steering force. Consequently the main benefit from ABS operation is to maintain directional control of the vehicle during heavy braking. In rare circumstances the stopping distance may be increased however, the directional control of the vehicle is substantially greater than if the wheels are locked up. The main difficulty in the design of ABS control arises from the strong nonlinearity and unc ertainty of the prob- lem. It is difficult and in many cases impossible to solve this problem by using classical linear, frequency domain methods [17]. ABS systems are designed around system hydraulics, sensors and control electronics. These sys- tems are dependent on each other and the different sys- tem components are interchangeable with minor changes in the controller software [18]. The wheel sensor feeds the wheel spin velocity to the electronic control unit, which based on some underlying control approach would give an output signal to the brake actuator control unit. The brake actuator control unit then controls the brake actuator based on the output from the electronic control unit. The control logic is based on the objective to keep the wheels from getting locked up and to maintain the traction between the tire and road surface at an optimal maximum. The task of keeping the wheels operating at maximum traction is complicated given that the friction-slip curve changes with vehicle, tire and road changes. The block diagram in Figure 3. shows the block representation of an antilock brake system. It shows the basic functionality of the various components in ABS systems and also shows the data/information flow. The ABS (shown in Figure 4) consists of a conven- tional hydraulic brake system plus antilock components. Copyright © 2011 SciRes. ICA 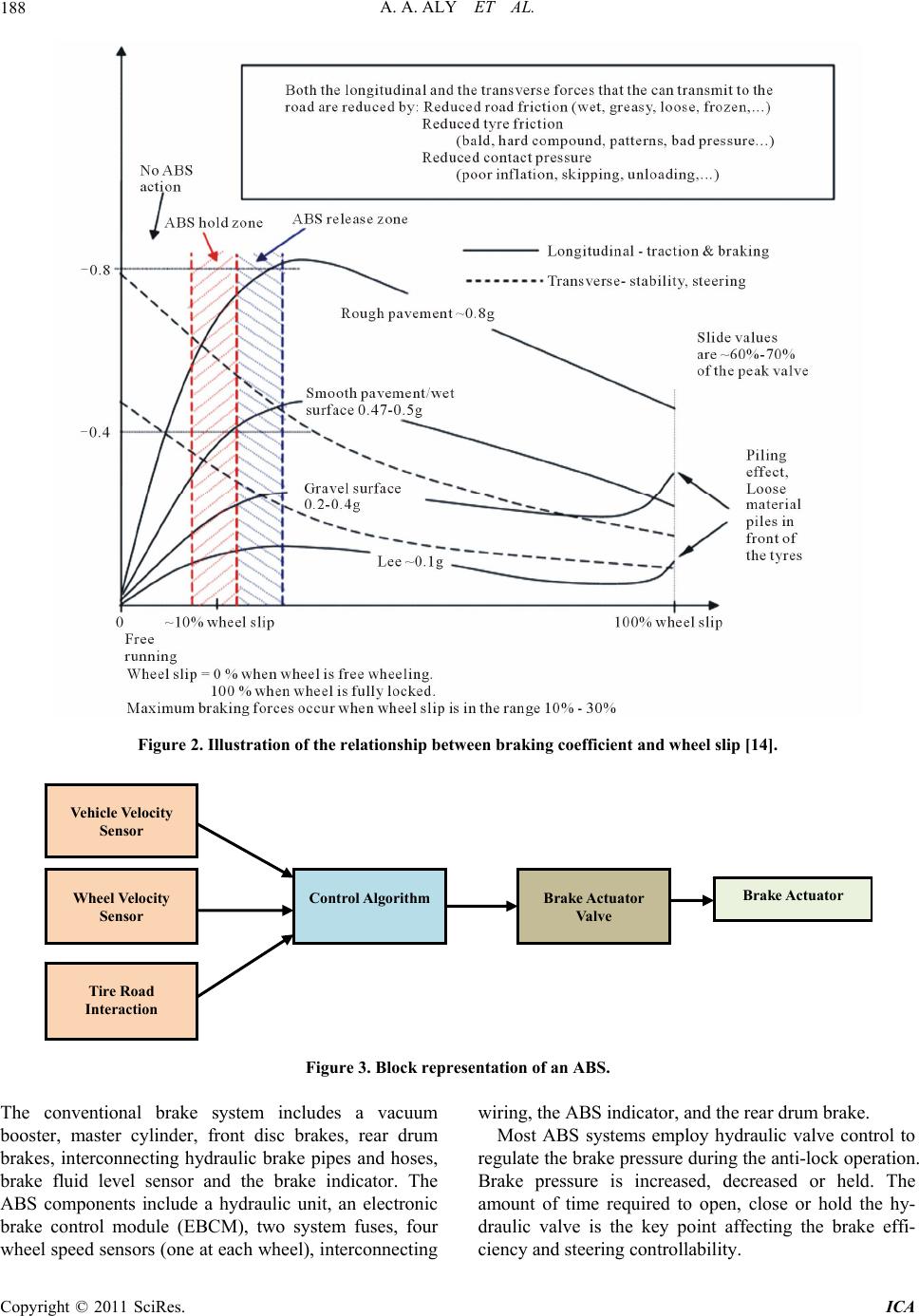 A. A. ALY ET AL. 188 Figure 2. Illustration of the relationship between braking coefficient and wheel slip [14]. Wheel Velocit y Sensor Vehicle Velocity Sensor Tire Road Interaction Control AlgorithmBrak e Actuat or Valve Brak e Actuat or Figure 3. Block representation of an ABS. The conventional brake system includes a vacuum booster, master cylinder, front disc brakes, rear drum brakes, interconnecting hydraulic brake pipes and hoses, brake fluid level sensor and the brake indicator. The ABS components include a hydraulic unit, an electronic brake control module (EBCM), two system fuses, four wheel speed sensors (one at each wheel), interconnecting wiring, the ABS indicator, and the rear drum brake. Most ABS systems employ hydraulic valve control to regulate the brake pressure during the anti-lo ck operation. Brake pressure is increased, decreased or held. The amount of time required to open, close or hold the hy- draulic valve is the key point affecting the brake effi- iency and steering con trollability. c Copyright © 2011 SciRes. ICA 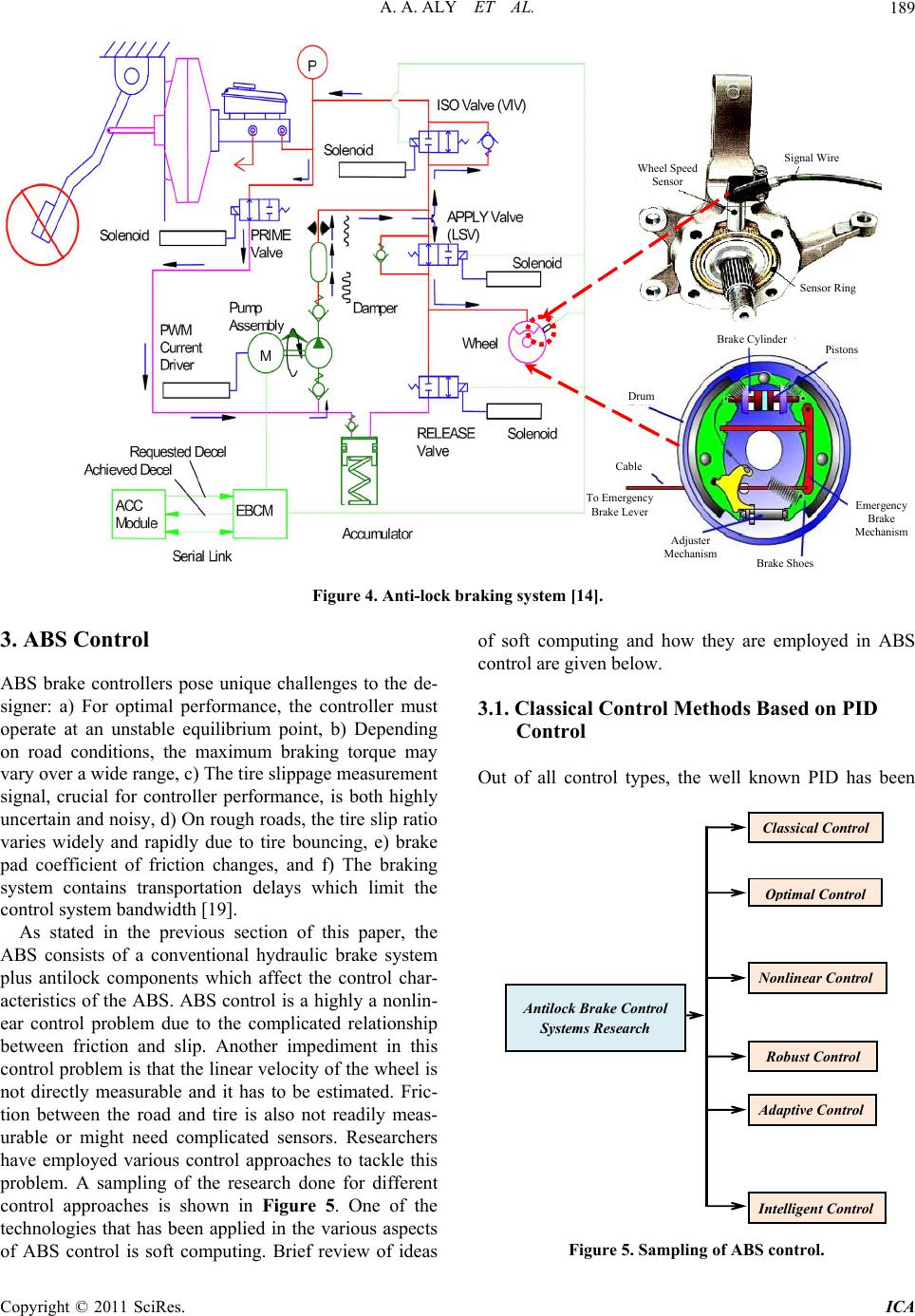 A. A. ALY ET AL.189 Signal Wire Wd heel Spee Sensor Sensor Ring Brake Cylinder Pistons Drum Cable T y Br er o Emergenc ake LevEmergency Brake Mechanism Adjuster Mechanism Brake Shoes Figure 4. Anti-lock braking system [14]. 3. ABS Control ABS brake controllers pose unique challenges to the de- signer: a) For optimal performance, the controller must operate at an unstable equilibrium point, b) Depending on road conditions, the maximum braking torque may vary over a wide range, c) The tire slippage measurement signal, crucial for controller performance, is both highly uncertain and noisy, d) On rough roads, the tire slip ratio varies widely and rapidly due to tire bouncing, e) brake pad coefficient of friction changes, and f) The braking system contains transportation delays which limit the control system bandwidth [19]. As stated in the previous section of this paper, the ABS consists of a conventional hydraulic brake system plus antilock components which affect the control char- acteristics of the ABS. ABS control is a h ighly a nonlin- ear control problem due to the complicated relationship between friction and slip. Another impediment in this control problem is that the linear velo city of the wheel is not directly measurable and it has to be estimated. Fric- tion between the road and tire is also not readily meas- urable or might need complicated sensors. Researchers have employed various control approaches to tackle this problem. A sampling of the research done for different control approaches is shown in Figure 5. One of the technologies that has been applied in the various aspects of ABS control is soft computing. Brief review of ideas of soft computing and how they are employed in ABS control are giv e n bel o w. 3.1. Classical Control Methods Based on PID Control Out of all control types, the well known PID has been Antilock Brake Control stems esearch Classical Control Intelligent Control Robust Control O timal Control Adaptive Control Nonlinear Con trol Figure 5. Sampling of ABS control. Copyright © 2011 SciRes. ICA  A. A. ALY ET AL. 190 used to improve the performance of the ABS. Song, et al. [20] presented a mathematical model that is designed to analyze and improve the dynamic performance of a ve- hicle. A PID controller for rear wheel steering is de- signed to enhance the stability, steerability, and drive- ability of the vehicle during transient maneuvers. The braking and steering performances of controllers are evaluated for variou s driving conditions, such as straight and J-turn maneuvers. The simulation results show that the proposed full car model is sufficient to predict vehi- cle responses accurately. The developed ABS reduces the stopping distance and increases the longitudinal and lateral stability of both two- and four-wheel steering ve- hicles. The results also demonstrate that the use of a rear wheel controller as a yaw motion controller can increase its lateral stability and reduce the slip angle at high speeds. The PID controller is simple in design but there is a clear limitation of its performance. It does not posses enough robustness for practical implementation. For solving this problem, Jiang [21] app lied a new Nonlinear PID (NPID) control algorithm to a class of truck ABS problems. The NPID algorithm combines the advantages of robust control and easy tuning. Simulation results at various situations using TruckSim show that NPID controller has shorter stopping distance and better velocity performance than the conventional PID controller and a loop-shaping controller. 3.2. Optimal Control Methods Based on Lyapunov approach The optimal control of nonlinear system such as ABS is one of the most challenging and difficult subjects in con- trol theory. Tanelli et al. [22] proposed a nonlinear out- put feedback control law for active braking control sys- tems. T he control law gu arantees bound ed control actio n and can cope also with input constraints. Moreover, the closed-loop system properties are such that the control algorithm allows detecting without the need of a friction estimator, if the closed-loop system is operating in the unstable region of the friction curve, thereby allowing enhancing both braking performance and safety. The design is performed via Lyapunov-based methods and its effectiveness is assessed via simulations on a multibody vehicle simulator. The ch ange in the road conditions im- plies continuous adap tation in controller parameter. In order to resolve this issue, an adaptive control- Lyapunov approach is suggested by R. R. Freeman [23] and similar ideas are pursued in [24,25]. The use of Son- tag’s formula is applied in the adap tiv e con tro l Lyapunov approach in [26], which includes gain scheduling on ve- hicle speed and experimental testing. Feedback lineariza- tion in combinatio n with gain scheduling is suggested by Liu and Sun [27]. PID-type approaches to wheel slip control are considered in [28-32]. A gain scheduled LQ control design approach with associated analysis, and, except [26] and [32], is the only one that contains de- tailed experimental evaluation using a test vehicle. In [33], an optimum seeking app roach is taken to determine the maximum friction, using sliding modes. Sliding mode control is also considered in [34,35]. Another nonlinear modification was suggested by Ün- sal and Kachroo [36] for observer-based design to con- trol a vehicle traction that is important in providing safety and obtaining desired longitudinal vehicle motion. The direct state feedback is then replaced with nonlinear observers to estimate the veh icle velocity from the ou tpu t of the system (i.e., wheel velocity). The nonlinear model of the system is shown locally observable. The effects and drawbacks of the extended Kalman filters and slid- ing observers are shown via simulations. The sliding observer is found promising while the extended Kalman filter is unsatisfactory due to unpredictable changes in the road conditions. 3.3. Nonlinear Control Based on Backstepping Control Design The complex nature of ABS requiring feedback control to obtain a desired system behavior also gives rise to dynamical systems. Ting and Lin [37] developed the anti-lock braking control system integrated with active suspensions applied to a quarter car model by employing the nonlinear backstepping design schemes. In emer- gency, although the braking distance can be reduced by the control torque from disk/drum brakes, the braking time and distance can be further improved if the normal force generated from active suspension systems is con- sidered simultaneously. Individual controller is designed for each subsystem and an integrated algorithm is con- structed to coordinate these two subsystems. As a result, the integration of an ti-lock braking and active suspen sion systems indeed enhances the system performance be- cause of reducti on o f braking time and distance . Wang, et al. [38] compared the design process of backstepping appro ach ABS via multiple model adap tive control (MMAC) controllers. The high adhesion fixed model, medium adhesion fixed model, low adhesion fixed model and adaptive model were four models used in MMAC. The switching rules of different model con- trollers were also presented. Simulation was conducted for ABS control system using MMAC method basing on quarter vehicle model. Results show that this method can control wheel slip ratio more accurately, and has higher robustness, therefore it improves ABS performance ef- Copyright © 2011 SciRes. ICA  A. A. ALY ET AL.191 fectively. Tor Arne Johansen, [39] provided a contribution on nonlinear adaptive backstepping with estimator resetting using multiple observers A multiple model based ob- server/estimator for the estimation of parameters was used to reset the parameter estimation in a conventional Lyapunov based nonlinear adaptive controller. Transient performance can be improved without increasing the gain of the controller or estimator. This allows perform- ance to be tuned without compromising robustness and sensitivity to noise and disturbances. The advantages of the scheme are demonstrated in an automotive wh eel slip controller. 3.4. Robust Control Based on Sliding Mode Control Method Sliding mode control is an important robust control ap- proach. For the class of systems to which it applies, slid- ing mode controller design provides a systematic ap- proach to the problem of maintaining stability and con- sistent performance in the face of modeling imprecision. On the other hand, by allowing the tradeoffs between modeling and performance to be quantified in a simple fashion, it can illuminate the whole design process. Several results have been published coupling the ABS problem and the VSS design technique [40,41]. In these works design of sliding-mode controllers under the as- sumption of knowing the optimal value of the target slip was introduced. A problem of concern here is the lack of direct slip measurements. In all previous investigations the separation approach has been used. The problem was divided into the problem of optimal slip estimation and the problem of tracking the estimated o ptimal value. J.K. Hedrick, et al. [42,43] suggested a modification of the technique known as sliding mode control. It was chosen due to its robustness to modeling errors and disturbance rejection capabilities. Simulation results are presented to illustrate the capability of a vehicle using this controller to follow a desired speed trajectory while maintaining constant spacing between vehicles. Therefore a sliding mode control algorithm was implemented for this appli- cation. While Kayacan [44] proposed a grey slid- ing-mode controller to regulate the wheel slip , depending on the vehicle forward velocity. The proposed controller anticipates the upcoming values of wheel slip and takes the necessary action to keep the wheel slip at the desired value. The performance of the control algorithm as ap- plied to a quarter vehicle is evaluated through simula- tions and experimental studies that include sudden changes in road conditions. It is observed that the pro- posed controller is capable of achieving faster conver- gence and better noise response than the conventional approaches. It is concluded that the use of grey system theory, which has certain pred iction cap abilities, can be a viable alternative approach when the conventional con- trol methods cannot meet the desired performance speci- fications. In real systems, a switched controller has im- perfections which limit switching to a finite frequency. The oscillation with the neighborhood of the switching surface cause chattering. Chattering is undesirable, since it involves extremely high control activity, and further- more may excite high-frequency dynamics neglected in the course of modeling. Chattering must be reduced (eliminated) for the controller to perform properly. 3.5. Adaptive Control Based on Gain Scheduling Control Method Ting and Lin [45] presented an approach to incorporate the wheel slip constraint as a priori into control design so that the skidding can be avoided. A control structure of wheel torque and wheel steering is proposed to transfor m the original problem to that o f state regulation with input constraint. For the transformed problem, a low-and-high gain technique is applied to construct the constrained controller and to enhance the utilization o f the wheel slip under constraint. Simulation shows that the proposed control scheme, during tracking on a snow road, is capa- ble of limiting the wheel slip, and has a satisfactory co- ordination between wheel torque and wheel steering. 3.6. Intelligent Control Based on Fuzzy Logic FC has been proposed to tackle the problem of ABS for the unknown environmental parameters [46-50]. How- ever, the large amount of the fuzzy rules makes the analysis complex. Some researchers have proposed fuzzy control design methods based on the sliding-mode con- trol (SMC) scheme. These approaches are referred to as fuzzy sliding-mode control (FSMC) design methods [51,52]. Since only one variable is defined as the fuzzy input variable, the main advantage of the FSMC is that it requires fewer fuzzy rules than FC does. Moreover, the FSMC system has more robustness against parameter variation [52]. Although FC and FSMC are both effec- tive methods, their major drawback is that the fuzzy rules should be previously tuned by time-consuming trial-and- error procedures. To tackle this problem, adaptive fuzzy control (AFC) based on the Lyapunov synthesis ap- proach has been extensively studied [52-55]. With this approach, the fuzzy rules can be automatically adjusted to achieve satisfactory system response by an adaptive law. Kumar et al. [56] investigated the in tegrated contro l of ABS System and collision avoidance system (CAS) in Copyright © 2011 SciRes. ICA  A. A. ALY ET AL. 192 electric vehicle. Fuzzy logic techniques are applied for integral control of two subsystems. Control algorithm is implemented and tested in a prototype electric vehicle in laboratory environment using free scale HCS12 micro- controller. A high level network protocol CAN is applied to integrate all sensors, ABS and CAS. The results show that integrated control of ABS and CAS maintains the safe distance from obstacle without sacrificing the per- formance of either system. Different researcher [57-59] developed an adaptive PID-type fuzzy controller for the ABS system. A platform is built to accomplish a series of experiments to control the ABS. A commercial ABS module controlled by a controller is installed and tested on the platform. The vehicle and tire models are deduced and simulated by a personal computer for real time con- trol. Road surface conditions, vehicle weight and control schemes are varied in the experiments to study braking properties. Lin and Hsu [60] proposed a self-learning fuzzy slid- ing-mode control (SLFSMC) design method for ABS. In the proposed SLFSMC system, a fuzzy controller is the main tracking controller, which is used to mimic an ideal controller; and a robust controller is derived to compen- sate for the difference between the ideal controller and the fuzzy controller. The SLFSMC has the advantages that it can automatically adjust th e fuzzy rules, similar to the AFC, and can reduce the fuzzy rules, similar to the FSMC. Moreover, an error estimation mechanism is in- vestigated to observe the bound of approximation error. All parameters in SLFSMC are tuned in the Lyapunov sense, thus, the stab ility of the system can be guaranteed. Finally, two simulation scenarios are examined and a comparison between a SMC, an FSMC, and the proposed SLFSMC is made. The ABS system performance is examined on a quar- ter vehicle model with nonlinear elastic suspension. The parallelism of the fuzzy logic evaluation process ensures rapid computation of the controller output signal, requir- ing less time and fewer computation steps than control- lers with adaptive identification. The robustness of the braking system is investigated on rough roads and in the presence of large measurement noise. The simulation results present the system performance on various road types and under rapidly changing road conditions. While conventional control approaches and even direct fuzzy/ knowledge based approaches [61-67] have been suc- cessfully implemented, their performance will still de- grade when adverse road conditions are encountered. The basic reason for this performance degradation is that the control algorithms have limited ability to learn how to compensate for the wide variety of road conditions that exist. Laynet et al. [68] and Laynet and Passino [69] intro- duced the idea of using the fuzzy model reference learn- ing control (FMRLC) technique for maintaining ade- quate performance even under adverse road conditions. This controller utilizes a learning mechanism which ob- serves the plant outputs and adjusts the rules in a direct fuzzy controller so that the overall system be haves like a “reference model” which characterizes the desired be- havior. The performance of the FMRLC-based ABS is demonstrated by simulation for various road conditions (wet asphalt, icy) and “split road conditions” (the condi- tion where, e.g., emergency braking occurs and the road switches from wet to icy or vice versa). Precup et al. [70] developed a Takagi-Sugeno fuzzy controller and an in- terpolative fuzzy controller for tire slip control in ABS systems. By employing local linearized models of the controlled plant, the local controllers are developed in the frequency domain. Development methods for the two fuzzy controllers are also offered. Simulation results show that the control system performance enhancement ensured by the fuzzy controllers in comparison with the conventional PI ones. Stan, et al. [71] performed a critical analysis of five fuzzy control solutions dedicated to ABS systems. The detailed mathematical model of controlled plant is de- rived and simplified for control design with focus on tire slip control. A new fuzzy control solution based on a class of Takagi-Sugeno fuzzy controllers is proposed. This class of fuzzy controllers combines separately de- signed PI and PID controllers corresponding to a set of simplified models of controlled plant linearized in the vicinity of importan t operating points. Simulation resu lts validate the suggested fuzzy control solution in control- ling the relative slip of a single wheel. R. Keshmiri and A.M. Shahri [72] designed an in telli- gent fuzzy ABS controller to adjust slipping performance for variety of roads. There are two major features in the proposed control system: the first is a fuzzy logic con- troller providing optimal brake torque for both front and rear wheels; and the second is also a FLC provides re- quired amount of slip and torque references properties for different kinds of roads. Simulation results show more reliable and better performance compared with other brake systems. While Karakose and Akin [73] proposed a different fuzzy control algorithm, which used dynamical fuzzy logic system and block based neural network, for dynamical control problems. The effective- ness of the proposed method is illustrated by simulation results for dc motor position control problem. In the same direction Ayman A. Aly [74] designed an intelli- gent fuzzy ABS controller to adjust slipping performance for variety of roads. The fuzzy optimizer finds immedi- ately the optimal wheel slips for the new surface and forces the actual wheel slips to track the optimal refer- Copyright © 2011 SciRes. ICA  A. A. ALY ET AL.193 ence wheel slips. The simulation results show that the proposed ABS algorithm ensures avoiding of wheel’s blockage, even in different road conditions. Moreover, as a free model strategy, the obtained fuzzy control is ad- vantageous from viewpoint of reducing design complex- ity and, also, antisatur ating, antich attering an d robu stness properties of the controlled system. 4. Conclusions ABS control is highly nonlinear control problem due to the complicated relationship between its components and parameters. The research that has been carried out in ABS control systems covers a broad range of issues and challenges. Many different control methods for ABS have been developed and research on improved control methods is continuing. Most of these approaches require system models, and some of them cannot achieve satis- factory performance under the changes of various road conditions. While soft computing methods like Fuzzy control doesn’t need a precise model. A brief idea of how soft computing is employed in ABS control is given. 5. Acknowledgement This study is supported by Taif University under a con- tract No. 1-432-1168. The financial support of Taif Uni- versity is highly appreciated. 6. References [1] P. M. Hart, “Review of Heavy Vehicle Braking Systems Requirements (PBS Requirements),” Draft Report, 24 April 2003. [2] M. Maier and K. Muller “The New and Compact ABS Unit for Passenger Cars,” SAE Paper No.950757, 1996. [3] P. E. Wellstead and N. B. O. L. Pettit, “Analysis and Redesign of an Antilock Brake System Controller,” IEE Proceedings Control Theory Applications, Vol. 144, No. 5, 1997, pp. 413-426. doi:10.1049/ip-cta:19971441 [4] A. G. Ulsoy and H. Peng, “Vehicle Control Systems,” Lecture Notes, ME 568, 1997. [5] P. E. Wellstead, “Analysis and Redesign of an Antilock Brake System Controller,” IEEE Proceedings Control Theory Applications, Vol. 144, No. 5, September 1997, pp. 413-426. doi: 10.1049/ip-cta:19971441 [6] R. Fling and R. Fenton, “A Describing-Function Ap- proach to Antiskid Design,” IEEE Transactions on Ve- hicular Technology, Vol. VT-30, No. 3, 1981, pp. 134- 144. doi:10.1109/T-VT.1981.23895 [7] S. Yoneda, Y. Naitoh and H. Kigoshi, “Rear Brake Lock-Up Control System of Mitsubishi Starion,” SAE Paper, Washington, 1983. [8] T. Tabo, N. Ohka, H. Kuraoka and M. Ohba, “Automo- tive Antiskid System Using Modern Control Theory,” IEEE Proceedings, San Francisco, 1985, pp. 390-395. [9] H. Takahashi and Y. Ishikawa, “Anti-Skid Braking Con- trol System Based on Fuzzy Inference,” U.S. Patent No. 4842342, 1989. [10] R. Guntur and H. Ouwerkerk, “Adaptive Brake Control System,” Proceedings of the Institution of Mechanical Engineers, Vol. 186, No. 68. 1972, pp. 855-880. doi:10.1243/PIME_PROC_1972_186_102_02 [11] G. F. Mauer, “A Fuzzy Logic Controller for an ABS Braking System,” IEEE Transactions on Fuzzy Systems, Vol. 3, No. 4, 1995, pp. 381-388. doi:10.1109/91.481947 [12] W. K. Lennon and K. M. Passino, “Intelligent Control for Brake Systems,” IEEE Transactions on Control Systems Technology, Vol. 7, No. 2, 1999, pp. 188-202. [13] B. Lojko and P. Fuchs, “The Control of ASR System in a Car Based on the TMS320F243 DSP,” Diploma Thesis, Dept. of Radio & Electronics, Bratislava, 2002. [14] P. Hart, “ABS Braking Requirements,” Hartwood Con- sulting Pty Ltd , Victoria, June 2003. [15] Q. Ming, “Sliding Mode Controller Design for ABS Sys- tem,” MSc Thesis, Virginia Polytechnic Institute and State University, 1997. [16] M. Stan, R.-E. Precup and A. S. Paul, “Analysis of Fuzzy Control Solutions for Anti-Lock Braking Systems,” Jour- nal of Control Engineering and Applied Informatics, Vol. 9, No. 2, 2007, pp. 11-22. [17] S. Drakunov, U. Ozgiiner and P. Dix, “ABS Control Us- ing Optimum Search via Sliding Modes,” IEEE Transac- tion on Control Systems Technology, Vo1. 3 No. 1, March 1995, pp. 79-85. [18] National Semiconductor Inc., “Adaptive Braking Systems (ABS),” US Patent No. 3825305, 1974. [19] G. F. Mauer, “A Fuzzy Logic Controller for an ABS Braking System,” IEEE Transactions on Fuzzy Systems, Vol. 3, No. 4, 1995, pp. 381-388. doi: 10.1109/91.481947 [20] J. Song, H. Kim and K. Boo, “A study on an Anti-Lock Braking System Controller and Rear-Wheel Controller to Enhance Vehicle Lateral Stability,” Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, Vol. 221 No. 7, 2007, pp. 777- 787. doi:10.1243/09544070JAUTO225 [21] F. Jiang, “An Application of Nonlinear PID Control to a Class of Truck ABS Problems,” Proceedings of the 40th IEEE Conference on Decision and Control, Orlando, 2000, pp. 516-521. [22] M. Tanellia, A. Astolfi and S. M. Savaresi, “Robust Nonlinear Output Feedback Control for Brake by Wire Control Systems,” Automatica, Vol. 44, No. 4, 2008, pp. 1078-1087. doi:10.1016/j.automatica.2007.08.020 [23] R. Freeman, “Robust Slip Control for a Single Wheel,” University of California, Santa Barbara, 1995. [24] J. S. Yu, “A Robust Adaptive Wheel-Slip Controller for Antilock Brake System,” Proceedings of 36th IEEE Con- Copyright © 2011 SciRes. ICA  A. A. ALY ET AL. 194 ferrence on Decision Control, San Diego, 1997, pp. 2545-2546. [25] J. Yi, L. Alvarez, R. Horowitz and C. C. DeWit, “Adap- tive Emergency Braking Control Using a Dynamical Tire/Road Friction Model,” Proceedings of 39th IEEE Conference on Decision Control, Sydney, 2000, pp. 456- 461. [26] J. Lüdemann, “Heterogeneous and Hybrid Control with Application in Automotive Systems,” Ph.D. dissertation, Glasgow University, 2002. [27] Y. Liu and J. Sun, “Target Slip Tracking Using Gain-Scheduling for Braking Systems,” Proceedings of the 1995 American Control Conference, Seattle, 1995, pp. 1178-1182. [28] S. Taheri and E. H. Law, “Slip Control Braking of an Automobile during Combined Braking and Steering Ma- noeuvres,” American Society of Magazine Editors, Vol. 40, No. 1, 1991, pp. 209-227. [29] C. Jun, “The Study of ABS Control System with Differ- ent Control Methods,” Proceedings of the 4th Interna- tional Symposium on Advanced Vehicle Control, Nagoya, 1998, pp. 623-628. [30] F. Jiang, “A Novel Approach to a Class of Antilock Brake Problems,” Ph.D. Dissertation, Cleveland State University, Cleveland, 2000. [31] Y. Wang, T. Schmitt-Hartmann, M. Schinkel and K. J. Hunt, “A New Approach to Simultaneous Stabilization and Strong Simultaneous Stabilization with D Stability and Its Application to ABS Control Systems Design,” European Control Conference, Porto, 2001, pp. 1291- 1294. [32] S. Solyom, “Synthesis of a Model-Based Tire Slip Con- troller,” Synthesis of a Model-Based Tire Slip Controller, Vol. 41, No. 6, 2004, pp. 475-499. [33] S. Drakunov, Ü. Özgüner, P. Dix, and B. Ashrafi, “ABS Control Using Optimum Search via Sliding Modes,” IEEE Transactions on Control Systems Technology, Vol. 3, 1995, pp. 79-85. doi:10.1109/87.370698 [34] M. Schinkel and K. Hunt, “Anti-lock Braking Control Using a Sliding Mode Like Approach,” Proceedings of the 2002 American Control Conference, Anchorage, 2002, pp. 2386-2391. [35] M. C. Wu and M. C. Shih, “Hydraulic Anti-Lock Braking Control Using the Hybrid Sliding-Mode Pulse Width Modulation Pressure Control Method,” Proceedings of the Institution of Mechanical Engineers, Vol. 215, 2001, pp. 177-187. doi:10.1109/87.748153 [36] C. Ünsal and P. Kachroo, “Sliding Mode Measurement Feedback Control for Antilock Braking Systems,” IEEE Transactions on Control Systems Technology, Vol. 7, No. 2, March 1999, pp. 271-281. [37] W. Ting and J. Lin, “Nonlinear Control Design of Anti-lock Braking Systems Combined with Active Sus- pensions,” Technical report of Department of Electrical Engineering, National Chi Nan University, 2005. [38] R.-G. Wang, Z.-D. Liu and Z.-Q. Qi, “Multiple Model Adaptive Control of Antilock Brake System via Back- stepping Approach,” Proceedings of 2005 International Conference on Machine Learning and Cybernetics, Guangzhou, 2005, pp. 591-595. [39] T. A. Johansen, J. Kalkkuhl, J. Lüdemann and I. Petersen, “Hybrid Control Strategies in ABS,” Proceedings of the 2001 American Control Conference, Arlington 2001, pp. 1704-1705. [40] H. S. Tan and M. Tomizuka, “An Adaptive Sliding Mode Vehicle Traction Controller Design,” Proceedings of the 1989 American Control Conference, Pittsburgh, 1989, pp. 1053-1058. [41] Y. K. Chin, W. C. Lin and D. Sidlosky, “Sliding-Mode ABS Wheel Slip Control,” Proceedings of 1992 ACC, Chicago, 1992, pp. 1-6. [42] J. C. Gerdes, A. S. Brown and J. K. Hedrick, “Brake System Modeling for Vehicle Control,” Proceedings In- ternational Mechanical Engineering Congress and Expo- sition, San Francisco, 1995, pp. 4756-4763. [43] D. Cho and J. K. Hedrick, “Automotive Powertrain Mod- eling for Control,” Transactions ASME Journal of Dy- namic Systems, Measurements and Control, Vol.111, No.4, December 1989, pp. 568-576. doi:10.1115/1.3153093 [44] E. Kayacan and O. Kaynak, “A Grey System Modeling Approach for Sliding Mode Control of Antilock Braking System,” IEEE Transactions On Industrial Electronics, Vol. 56, No. 8, August 2009, pp. 3244-3252. doi:10.1109/TIE.2009.2023098 [45] W. Ting and J. Lin, “Nonlinear Control Design of Anti-lock Braking Systems Combined with Active Sus- pensions,” Technical Report of Department of Electrical Engineering, National Chi Nan University, 2005. [46] B. Ozdalyan, “Development of A Slip Control Anti-Lock Braking System Model,” International Journal of Auto- motive Technology, Vol. 9, No. 1, 2008, pp. 71-80. doi:10.1007/s12239-008-0009-6 [47] A. B. Will and S. H. Zak, “Antilock Brake System Mod- elling and Fuzzy Control,” International Journal of Vehi- cle Design, Vol. 24, No. 1, 2000, pp. 1-18. doi:10.1504/IJVD.2000.001870 [48] J. R. Layne, K. M. Passino and S. Yurkovich, “Fuzzy Learning Control for Antiskid Braking Systems,” IEEE Transactions on Control Systems Technology, Vol. 1, No. 2, 1993, pp. 122-129. doi:10.1109/87.238405 [49] G. F. Mauer, “A Fuzzy Logic Controller for an ABS Braking System,” IEEE Transactions on Fuzzy Systems, Vol. 3, No. 4, 1995, pp. 381-388. doi:10.1109/91.481947 [50] K. Lee and K. Park, “Optimal Robust Control of a Con- tactless Brake System Using an Eddy Current,” Mecha- tronics, Vol. 9, No. 6, 1999, pp. 615-631. doi:10.1016/S0957-4158(99)00008-2 [51] W. K. Lennon and K. M. Passino, “Intelligent Control for Brake Systems,” IEEE Transctions on Control Systems Technology, Vol. 7, No. 2, 1999, pp. 188-202. doi:10.1109/87.748145 [52] C. Unsal and P. Kachroo, “Sliding Mode Measurement Copyright © 2011 SciRes. ICA  A. A. ALY ET AL. Copyright © 2011 SciRes. ICA 195 Feedback Control for Antilock Braking Systems,” IEEE Transctions on Control Systems Technology, Vol. 7, No. 2, 1999, pp. 271-280. doi:10.1109/87.748153 [53] C.C. Lee, “Fuz zy Logic in Cont rol Systems: Fuzzy Logic Controller Part I, II,” IEEE Transactions on Systems, Man, and Cybernetics, Vol. 20, No. 2, 1990, pp. 404-435. doi:10.1109/21.52551 [54] S.W. Kim and J.J. Lee, “Design of a Fuzzy Controller with Fuzzy Sliding Surface,” Fuzzy Sets and Systems, Vol. 71, No. 3, 1995, pp. 359-369. doi:10.1016/0165-0114(94)00276-D [55] B. J. Choi, S. W. Kwak and B. K. Kim, “Design of a Single-Input Fuzzy Logic Controller and Its Properties,” Fuzzy Sets Systems, Vol. 106, No. 3, 1999, pp. 299-308. doi:10.1016/S0165-0114(97)00283-2 [56] S. Kumar, K. L. Verghese and K. K. Mahapatra, “Fuzzy Logic Based Integrated Control of Anti-Lock Brake Sys- tem and Collision Avoidance System Using CAN for Electric Vehicles,” IEEE International Conference on Industrial Technology, Gippsland, 2009, pp. 1-5. doi:10.1109/ICIT.2009.4939720 [57] L. X. Wang, “Adaptive Fuzzy Systems and Control: De- sign and Stability Analysis,” Prentice-Hall, Inc., Upper Saddle River, 1994. [58] H. Lee and M. Tomizuka, “Robust Adaptive Control Using a Universal Approximator for SISO Nonlinear Systems,” IEEE Transactions on Fuzzy Systems, Vol. 8, No. 1, 2001, pp. 95-106. [59] C. K. Chen and M. C. Shih, “PID Type Fuzzy Control for Antilock Brake System with Parameter Adaptation,” JSME International Journal, Series C, Vol. 47, No. 2, 2004, pp. 675-685. doi:10.1299/jsmec.47.675 [60] C.-M. Lin, C.-F. Hsu, “Self-Learning Fuzzy Slid- ing-Mode Control for Antilock Braking Systems,” IEEE Transactions On Control Systems Technology, Vol. 11, No. 2, 2003, pp. 273-278. doi:10.1109/TCST.2003.809246 [61] H. Tan and M. Tomizuka, “A Discrete-Time Robust Ve- hicle Traction Controller Design,” American Controls Conference, Pittsburgh, 1989, pp. 1053-1058. [62] H. Tan and M. Tomizuka, “Discrete-Time Controller Design for Robust Vehicle Traction,” IEEE Control Sys- tems Magazine, Vol. 10, No. 3, 1990, pp. 107-113. doi:10.1109/37.55132 [63] R. Fling and R. Fenton, “A Describing-Function Ap- proach to Antiskid Design,” IEEE Transactions on Ve- hicular Technology, Vol. 30, No. 3, 1981, pp.134-144. doi:10.1109/T-VT.1981.23895 [64] S. Yoneda , Y. Naito h and H. Kigosh i, “Rea r Brake Lo ck- Up Control System of Mitsubishi Starion,” SAE paper 830482, 1983. [65] T. Tabo, N. Ohka, H. Kuraoka and M. Ohba, “Automo- tive Antiskid System Using Modern Control Theory,” IECON, Vol. 1, pp. 390-395, 1985. [66] H. Takahashi and Y. Ishikawa, “Anti-Skid Braking Con- trol System Based on Fuzzy Inference,” US Patent No. 4842342, 1989. [67] R. Guntur and H. Ouwerkerk, “Adaptive Brake Control System,” Proceedings of the Institution of Mechanical Engineers, 1972, pp. 855-880. [68] J. R. Laynet, K. M. Passinot and S. Yurkovich, “Fuzzy Learning Control for Anti-Skid Braking Systems,” IEEE Transactions on Control Systems Technology, Vol. 1, No. 2, 1993, pp. 122-129. doi:10.1109/87.238405 [69] J. Laynet and K. M. Passino, “Fuzzy Model Reference Learning Control for Cargo Ship Steering,” IEEE Control Systems Magazine, Vol. 13, No. 6, September 1992, pp. 23-24. doi:10.1109/37.248001 [70] R-E. Precup, St. Preitl, M. Balas, V. Balas, “Fuzzy Con- trollers for Tire Slip Control in Anti-lock Braking Sys- tems,” IEEE International Conference on Fuzzy Systems, Budapest, 2004, pp. 1317-1322. [71] M. Stan, R.-E. Precup and S. A. Paul, “Analysis of Fuzzy Control Solutions for Anti-Lock Braking Systems,” Journal of Control Engineering and Applied Informatics, Vol. 9, No. 2, 2007, pp. 11-22. [72] R. Keshmiri and A. M. Shahri, “Intelligent ABS Fuzzy Controller for Diverse Road Surfaces,” World Academy of Science, Engineering and Technology, Vol. 2, No. 2, 2007, pp. 62-67. [73] M. Karaköse and E. Akin, “Dynamical Fuzzy Control with Block Based Neural Network,” Technical Report, Department of Computer Engineering, Fırat University, 2006. [74] A. A. Aly, “Intelligent Fuzzy Control for Antilock Brake System with Road-Surfaces Identifier,” 2010 IEEE In- ternational Conference on Mechatronics and Automation, Xi’an, 2010, pp. 2292-2299.
|