Intelligent Control and Automation, 2011, 2, 196-202
doi:10.4236/ica.2011.23024 Published Online August 2011 (http://www.SciRP.org/journal/ica)
Autonomous Target Interception Using Hybrid Sensor
Networks*
Wenzhe Zhang1, Yihuai Wang1, Ying Li1, Minglu Li2
1School of Computer Science and Technology, Soochow University, Soochow, China
2Department of Com p uter Science and En gineering , Shanghai Jiaotong University, Shanghai, China
Received December 2, 2010; revised May 20, 2011; accepted May 27,2011
Abstract
Hybrid sensor networks (HSNs) comprise of mobile and static sensor nodes setup for purpose of collabora-
tively performing tasks like sensing a phenomenon or monitoring a region. In this paper, we present target
interception as a novel application using mobile sensor nodes as executor. Static sensor nodes sense, com-
pute and communicate with each other for navigation. Mobile nodes are guided to intercept target by the
static nodes nearby. Our approach does not require any prior maps of the environment thus, cutting down the
cost of the overall energy consumption. As to multi-targets multi-mobile nodes case, we present a PMB al-
gorithm for task assignment. Simulation results have verified the feasibility and effectiveness of our ap-
proach proposed.
Keywords: Target, Hybrid Sensor Networks, Interception, CoS, Intercepting Strategy, PMB Task
Assignment
1. Introduction
A networked system of hybrid sensor networks opens
new frontiers in variety of civilian and military applica-
tions and in some scientific disciplines. A mixture of
networked mobile robots and static sensors reduce the
cost but preserves the flexibility and advantageous capa-
bilities of a multi-robot system.
We are broadly interested in the mutually beneficial
collaboration between mobile and static sensor networks.
The underlying principle in this hybrid network between
the mobile and static nodes is th at: the static nodes serve
as the sensing, computation and communication medium,
whereas the robots provide action and finish the task of
blocking with the help of static sensors. In this work we
describe results from such a system which accurately and
reliably solves the problem of target interception. Some
properties of our appr oach are summarized below:
1) The sensor network is pre-deployed into the envi-
ronment deterministically or randomly for the full cov-
erage of the region.
2) After deployment, static sensor nodes can sense the
condition of its environment. By the multi-hop commu-
nication, static nodes compute the distributions of local
environment and evaluate appearance of the target.
3) The nodes of the sensor network are synchronized
in time (high precision is not required).
4) The mobile node is made up of a static sensor and a
robot, so it can communicate with any static nodes
nearby.
5) The environment is not required to be static.
Sensor networks are deployed in the field of interest.
They are expected to monitor the field and intercept any
intruding target as soon as possible in an unmanned
manner[1]. The concept of artificial potential fields for
the purpose of obstacle avoidance was presented in [2-6].
The concept of Vector Field Histograms (VFH) based on
locally constructed polar histograms for robot navigation
was presented in [7]. It may be noted that a parallel ap-
proach for the construction of a navigation field has been
proposed in sensor network. It uses potential fields and
the hop count to compute the magnitude of the direc-
tional vectors. In our paper, we only use the static node
nearby to guide the mobile node, which cut down the
complication of computation greatly.
*This paper is supported by the Natural Science Foundation of China,
N
o. 61070169, National Basic Research Program of China, No. 2006
CB303000 and Jiangsu Natural Sc ience Foundation No. 10KJB 520017.In this paper we propose a landmark-based pursuit

W. Z. ZHANG ET AL.197
strategy to address the problem of target interception. i.e.
When the target intrudes the sensory field, static sensor
nodes that detect the events collectively elect one head
that has sensed the largest intensity of signal. After data
computing, it will generate a sensing report and flood
over the network by multi-hops. We call the sensing re-
port data stimulus and the head node as center of stimu-
lus. Mobile sensor node acquires the position of target
and decides its optimal pursuit direction with the help of
sensors nearby. When the target moves, center of stimu-
lus is re-elected and static sensor node keeps the proper
position of the target. Only if the update of the network
is enough, can the mobile node select its optimal strateg y
to intercept the target. Instead of a mobile node wander-
ing randomly, in sign-based approach each static node
decides the direction to guide the mobile node. As a re-
sult, our approach with refreshing stimulus packets
adapts to the mobile target, and can guide the mobile
node to block the target as soon as possible.
We rely on the communication network to establish
the navigation paths. Also, in our approach the mobile
robots only need a local sense of target in order to move
toward the correct direction. The obvious merit is that
the mobile node does not need a pre-decided environ-
ment map, or a compass.
The rest of the paper is organized as follows: We pre-
sent sensing model, stimulus election and target localiza-
tion in Section 2 Mobile node navigation is presented in
Section 3. In Section 4 we extend the case to multiple
targets and mobile nodes and design the task assignment
algorithms. Section 5 presents the simulation and evalu-
ates its performance. Section 6 summarizes the work and
sketches out our future plan.
2. Sensor Network Surveillance
2.1. Sensing Model
Let
s
N be the number of static senor nodes, deployed
over the surveillance region . Let
2
R i
s
R be the
location of the i-th sensor node and let
is
. Let

iN:1Ss


,GSE

be a communica-
tion graph such that ,
ij
s
sE

if and only if node i
can communicate with node j. Let mbe the
number of mobile nodes (for simplicity, s
NN
1
m
N

) and
Let s be the sensing range of each static/mobile
sensor node. If there is a targ et at
R
x
R, the sensor node
can detect the presence of the target. Each sensor records
the sensor’s signal strength,
1ii
i i
ii
wifsx R
sx
S
wifsx








where

,

and

are constants specific to the sen-
sor type and they are normalized such that i has the
standard Gaussian distribution. This signal-strength
based sensor model is general for sensors available in
sensor networks, such as acoustic and magnetic sensors,
and has been used frequently [8-10]. For each sensori, if
i
w
S

, where

is a threshold set for appropriate val-
ues of detection and false-positiv e probabilities, the node
is activated and join in the mesh as shown in Figure 1. It
will participate in the stimulus election in the next sec-
tion and may transmit itsto its neighboring nodes if
necessary. i
S
2.2. Stimulus Election and Its Update
The election of a source follows the mechanism bellow.
We want only one node to generate the report since it
would be a waste of resour ces if every nod e detecting th e
target sends a report. The target creates a field of sensing
signal strength, the nearer the sensor is, the signal
strength it collects is larger.
Each node broadcasts a message indicating its signal
strength and Cartesian coordinate (with some random
delay to avoid collision). A node rebroadcasts its signal
strength whenever it hears a neighbor’s message with a
weaker signal, but stops broadcasting when it hears a
stronger one. In this way, messages roll throughout the
whole network of the signal strength field. Finally the
node with the strongest signal is elected as the Center of
Stimulus (CoS) and generates the sensing reports.
Vt
Figure 1. The stimulus starts from a source and ends at the
mobile node. The black nodes forward the packet to the
source collectively. Notice that some nodes outside of the
mesh also receive the packet but do not forward it.
s
s
R

(1)

W. Z. ZHANG ET AL. 198
2.3. Target Localization and Velocity Estimation
Computation of target’s information is performed by the
node CoS. Let i
x
be the Cartesian coordinate of sen-
sor , the position of a target is estimated as
i
1
1
*
ˆ
j
j
j
k
ii
j
ik
i
j
Sx
xS



 (2)
then ˆi
x
is broadcasted as stimulus data all through the
network. In this way, although each sensor cannot give
an accurate estimate of target’s position, as more sensors
collaborate, the accuracy of estimates improves [11].
We assume mobile sensor node can move at some cer-
tain velocity, here we note it as m. Target may intrude
into the monitoring region and move with the speed of
maximum .
v
t
Based on the target location, we can calculate the ve-
locity of the moving target as well. For simplicity, sup-
pose the estimated positions of target at time 1and
2are
v
t
t

111
ˆ,

x
xyand


222
ˆ,
x
xyrespectively, the
velocity of the target is computed as:

22
12 12
12
ˆt
xx yy
vtt

 (3)
And the direction of velocity 12
ˆˆ
:
t
x
x

.
3. Mobile Node Navigation
3.1. Interception Strategy
We suppose the mobile node moves at a constant speed.
In order to intercept the intruding target as soon as possi-
ble, we need select the optimal direction of movement
m

according to the instant target. The target may in-
trude the field of interest at any time with the velo city of
. At first, we consider the case of static target,
i.e. . As to the static target, the optimal strategy is
intercepting towards the target as shown in Figure 2. So
the intercept strategy is computed as:

max
t
vv0
t
v

t
222
arccos 2
SMMT TS
mSM MT
ddd
dd





(4)
where are Euclidean distances of Static
node-Mobile node, Mobile node-Target and Target-Sta-
tic node.
,,
SMMT TS
ddd
As to the mobile target, interception strategy needs
modified according to the update of targ et’s position and
velocity. Based on the velocity esti mation in Section 2C,
the additional offset of interception direction is computed
as:
arcsin sin
t
mm
v
v






m
(5)
So the optimal strategy of mobile target interception is
computed as shown in Figure 3:
mm




 (6)
3.2. Target Intercepting
During the interception perfo rmance, there are four states
for mobile sensor node, i.e. WAIT, LONG-DISTANCE:
NAVIGATE, SHORT-DISTANCE: TRACKING and
INTERCEPTED. In the beginning there is no target in-
truding into the region, so mobile node is waiting for a
command, maybe wandering randomly. When the target
appears in the region, CoS node injects the stimulus
packet into the sensor network and activates the compu-
tation to the position and velocity of the target. Receiv-
ing the stimulus Message, mobile node come to the
LONG-DISTANCE state and begins to navigate with the
guidance of static node nearby. When the sensor of mo-
bile node receives enough signal strength (above

), it
Figure 2. Intercepting static target.
Figure 3. Intercepting mobile target.

W. Z. ZHANG ET AL.199
will track the target in the current direction. Finally if the
position and velocity of mobile node is the same with
that of target, mission is completed. Note that when the
signal strength received is less than the threshold

, mo-
bile node’s state will transit from SHOT-DISTANCE to
LONG-DISTANCE, and co me back to navigate with the
help o f static nodes as shown in Figure 4.
3.3. Metrics of Interception
In the mission of target interception, sev eral criteria may
be chosen to evaluate the performance, such as minimi-
zation of mobile node’s energy while guaranteeing cap-
ture of all targets or maximization of number of captured
targets within a certain amount of time. In this work we
focus on minimizing the Time-to-Interception (TI) of
mobile node. Since target’s motion is not known, exact
TI is not known either; therefore we need to define a
metric to estimate TI. We will use the following defini-
tion of TI:
Definition 1. Let
 


2
00
,
tt
pt vt 
t
2
the posi-
tion and velocity of a target at time 0, and t
 


22

tt t
00 the position and velocity of
a mobile node at time 10 . We define the mini-
mum time TI necessary for the mobile node to reach the
target with the same velocity, assuming that the target
will keep moving with constant velocity, i.e.,
,
mm
pt vt
 
1111
min ,
tmtm
T
TI
TptTptTvtT vtT


where
   


101001
*,
tt
pt Tptt TtvtvtTvt 0 .
This definition allows us to quantify TI in an unambi-
guous way. Although target can change trajectories over
time, it is a more accurate estimate than, for example,
some metric based on the distance between the target and
WAIT: Wait
for start
LONG-
DISTANCE:
NAVIGATE
Msg:
Stimulus
SHORT-
DISTANCE:
TRACKING
m
S
<

CAPTURED
|MT| =0
m
S
>

Figure 4. States transition diagram of mobile node.
the mobile node, since TI incorporates the dynamics of
mobile node. Moreover, it is well-defined for any arbi-
trary time delay 10d
ttt

 in the estimate of target’s
position and velocity relative to current time 1. Given
this definition and the constraints on the dynamics of the
mobile node, it is possible to calculate explicitly TI.
t
4. Task Assignment Algorithms
In the previous section, we presented mobile sensor node
interception and its metric for an intercepting pa ir. In this
section we consider the case of multiple targets and mo-
bile nodes. Given positions and velocities of all targets
and mobile nodes, it is possible to compute TI matrix
,mt
N
N
ij
Cc   

c
, where m and t are the total
number of mobile nodes and targets, respectively, and
the entry ,ij of the matrix C corresponds to the ex-
pected TI between mobile node i and target j. When co-
ordinating multiple mobile nodes to intercept multiple
targets, it is necessary to select an assignment. Our ob-
jective is to select an assignment that minimizes the ex-
pected TI of all mobile nodes.
N N
Assume that we have the same number of mobile
nodes and targets, i.e. . An assignment can be
represented as a matrix ,
m
NNtmt
N
N
ij 
 

Xx , where the
entry ,ij
x
of the matrix X is equal to 1 if mobile node i
is assigned to target j, and equal to 0 otherwise. The as-
signment problem can therefore be written formally as
follows:



,,,
0,1 ,1,,
,,
11
min max
subject to 1, 1.
ij ijij
xij N
NN
ij ij
ij
cx
xx





 (7)
As formulated in the equation above, the assignment
problem appears as a combinatorial problem.
One simple greedy assignment algorithm that tries to
solve the optimization problem above is to look for the
smallest TI entry in the matrix C, assign the correspond-
ing interception pair, and remove the corresponding row
and column from the matrix C which now becomes of
dimension




1NN1

, and repeat the same process
until each mobile node is assigned to a target. Although
it is straightforward and easy to implement, this is a
suboptimal algorithm, since there are cases when the
greedy assignment gives the worst solution.
In this section we present a collaborative task assign-
ment protocol as Figure 5. The protocol assigns the task
based on probe message in a distributed manner. Previ-
ous work [11-13] gives a hierarchical multiple task as-
signment protocol for the similar problem. But all of
them are not distributed and is not scalable well.
Besides, we describe a simple random task assignment
algorithm as Randomly Task Assignment (RTA), i.e. in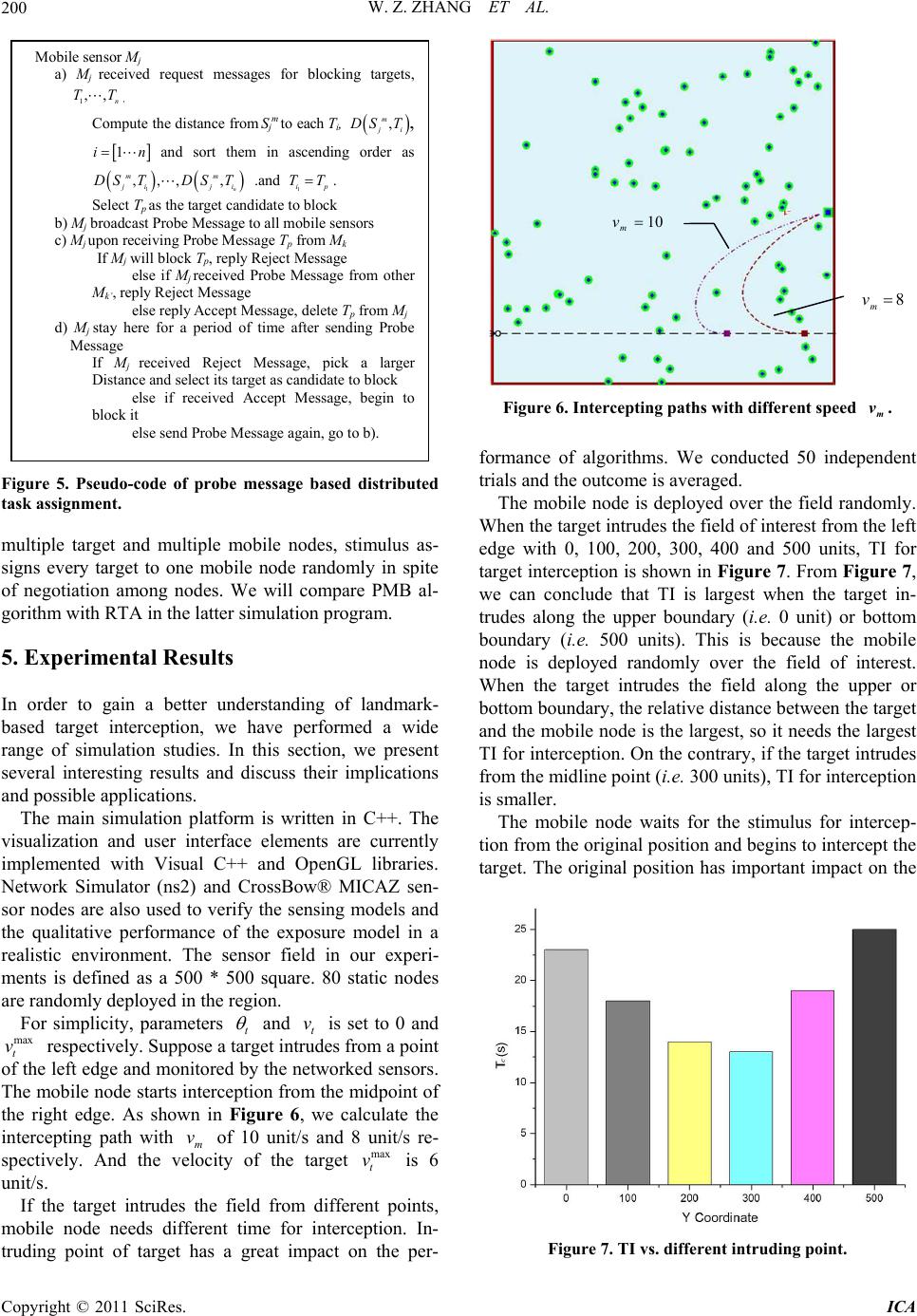

W. Z. ZHANG ET AL. 200
Mobile sensor M
j
a) M
j
received request messages for blocking targets,
1,, n
TT
,
Com put e th e dist anc e fr om
S
jm
to each T
i
,


,
m
ji
DS T
,


1in
and sort them in ascending order as
 
1
,,, ,
n
mm
ji ji
DS TDS T .and
1
ip
TT .
Select T
p
as th e ta rget candidate to block
b) M
j
broadcast Pr obe Mes sage to all mobile sensors
c) M
j
upon receivin g Probe Message T
p
from M
k
If M
j
will block T
p
, reply Reject Message
else if M
j
received Probe Message from other
M
k’
, reply Reject Message
else reply Accept Message, delete T
p
from M
j
d) M
j
stay here for a period of time after sending Probe
Message
If M
j
received Reject Message, pick a larger
Distance and selec t its target as candidate to block
else if received Accept Message, begin to
block it
else s end Probe Mess age again, go to b).
Figure 5. Pseudo-code of probe message based distributed
task assignment.
multiple target and multiple mobile nodes, stimulus as-
signs every target to one mobile node randomly in spite
of negotiation among nodes. We will compare PMB al-
gorithm with RTA in the latter simulation program.
5. Experimental Results
In order to gain a better understanding of landmark-
based target interception, we have performed a wide
range of simulation studies. In this section, we present
several interesting results and discuss their implications
and possible applications.
The main simulation platform is written in C++. The
visualization and user interface elements are currently
implemented with Visual C++ and OpenGL libraries.
Network Simulator (ns2) and CrossBow® MICAZ sen-
sor nodes are also used to verify the sensing models and
the qualitative performance of the exposure model in a
realistic environment. The sensor field in our experi-
ments is defined as a 500 * 500 square. 80 static nodes
are randomly deployed in the region.
For simplicity, parameters t

and t is set to 0 and
respectively. Suppose a target intrudes from a point
of the left edge and monitored by the networked sensors.
The mobile node starts interception from the midpoint of
the right edge. As shown in Figure 6, we calculate the
intercepting path with m of 10 unit/s and 8 unit/s re-
spectively. And the velocity of the target is 6
unit/s.
v
max
t
v
vmax
t
v
If the target intrudes the field from different points,
mobile node needs different time for interception. In-
truding point of target has a great impact on the per-
10
m
v
8

m
v
Figure 6. Intercepting paths with different speed .
m
v
formance of algorithms. We conducted 50 independent
trials and the outcome is averaged.
The mobile node is deployed over the field randomly.
When the target intru des the field of interest from the left
edge with 0, 100, 200, 300, 400 and 500 units, TI for
target interception is shown in Figure 7. From Figure 7,
we can conclude that TI is largest when the target in-
trudes along the upper boundary (i.e. 0 unit) or bottom
boundary (i.e. 500 units). This is because the mobile
node is deployed randomly over the field of interest.
When the target intrudes the field along the upper or
bottom boundary, the relative distance between the targ et
and the mobile node is the larg est, so it needs the largest
TI for interception. On the contrary, if the target intrudes
from the midline point (i.e. 300 units), TI for interception
is smaller.
The mobile node waits for the stimulus for intercep-
tion from the original po sition and begins to intercep t the
target. The original position has important impact on the
Figure 7. TI vs. different intruding point.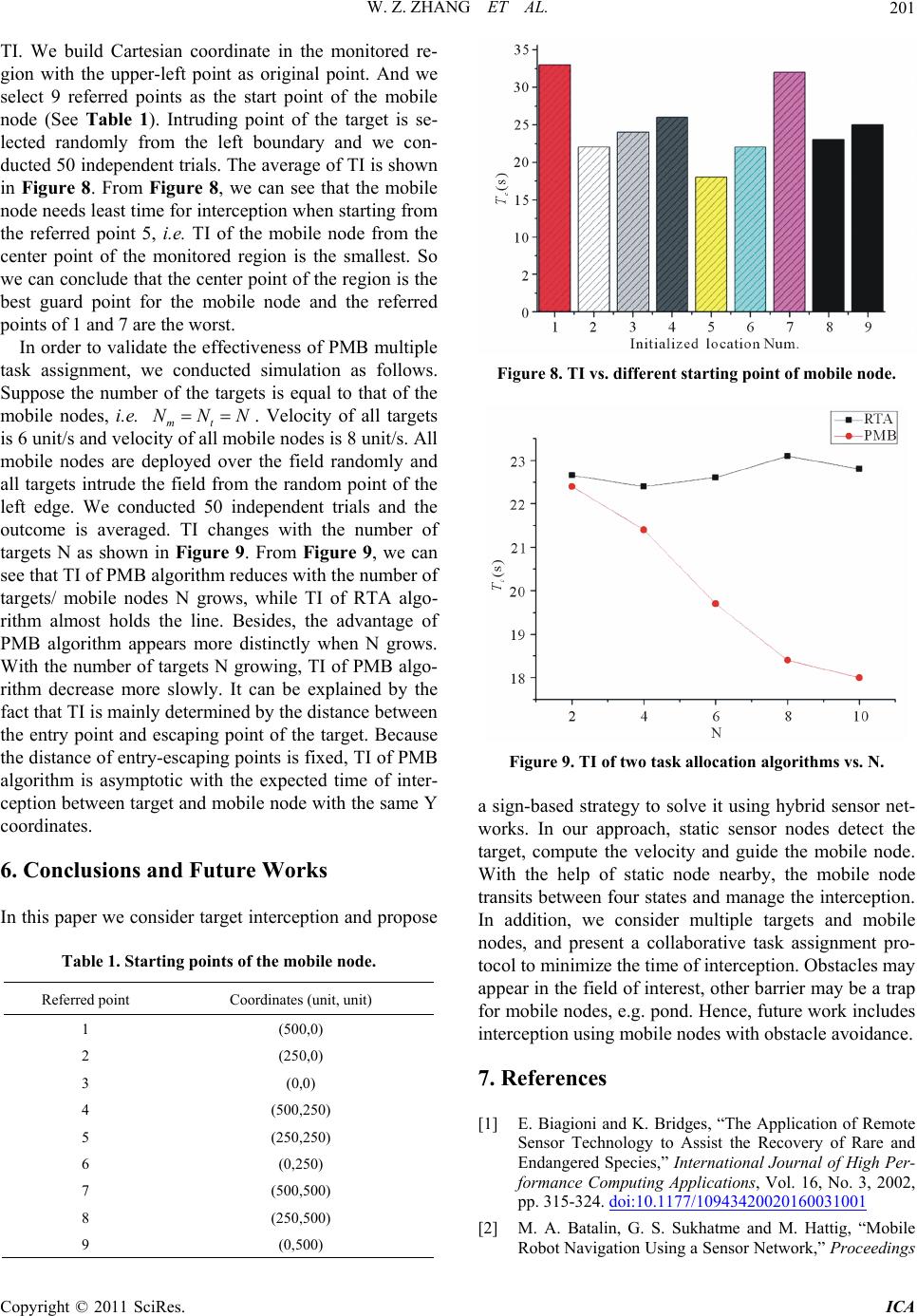

W. Z. ZHANG ET AL.201
TI. We build Cartesian coordinate in the monitored re-
gion with the upper-left point as original point. And we
select 9 referred points as the start point of the mobile
node (See Table 1). Intruding point of the target is se-
lected randomly from the left boundary and we con-
ducted 50 ind ependent trials. The average of TI is sh own
in Figure 8. From Figure 8, we can see that the mobile
node needs least time for interception when starting from
the referred point 5, i.e. TI of the mobile node from the
center point of the monitored region is the smallest. So
we can conclude that the center point of the region is the
best guard point for the mobile node and the referred
points of 1 and 7 are the worst.
In order to validate the effectiveness of PMB multiple
task assignment, we conducted simulation as follows.
Suppose the number of the targets is equal to that of the
mobile nodes, i.e. mt . Velocity of all targets
is 6 unit/s and velocity of all mobile nodes is 8 un it/s. All
mobile nodes are deployed over the field randomly and
all targets intrude the field from the random point of the
left edge. We conducted 50 independent trials and the
outcome is averaged. TI changes with the number of
targets N as shown in Figure 9. From Figure 9, we can
see that TI of PMB algorithm reduces with the number of
targets/ mobile nodes N grows, while TI of RTA algo-
rithm almost holds the line. Besides, the advantage of
PMB algorithm appears more distinctly when N grows.
With the nu mber of targ ets N growing, TI of PMB algo-
rithm decrease more slowly. It can be explained by the
fact that TI is mainly determined by the distance between
the entry point and escaping point of the target. Because
the distance of entry-escaping points is fixed, TI of PMB
algorithm is asymptotic with the expected time of inter-
ception between target and mobile node with the same Y
coordinates.
NNN
6. Conclusions and Future Works
In this paper we consider target interception and propo se
Table 1. Starting points of the mobile node.
Referred point Coordinates (unit, unit)
1 (500,0)
2 (250,0)
3 (0,0)
4 (500,250)
5 (250,250)
6 (0,250)
7 (500,500)
8 (250,500)
9 (0,500)
Figure 8. TI vs. different starting point of mobile node.
Figure 9. TI of two task allocation algorithms vs. N.
a sign-based strategy to solve it using hybrid sensor net-
works. In our approach, static sensor nodes detect the
target, compute the velocity and guide the mobile node.
With the help of static node nearby, the mobile node
transits between four states and manage the interception.
In addition, we consider multiple targets and mobile
nodes, and present a collaborative task assignment pro-
tocol to minimize the time of intercep tion. Obstacles may
appear in the field of interest, other barrier may be a trap
for mobile nodes, e.g. pond. Hence, future work includ es
interception using mobile nodes with obstacle avoidance.
7. References
[1] E. Biagioni and K. Bridges, “The Application of Remote
Sensor Technology to Assist the Recovery of Rare and
Endangered Species,” International Journal of High Per-
formance Computing Applications, Vol. 16, No. 3, 2002,
pp. 315-324. doi:10.1177/10943420020160031001
[2] M. A. Batalin, G. S. Sukhatme and M. Hattig, “Mobile
Robot Navigation Using a Sensor Network,” Proceedings

W. Z. ZHANG ET AL. 202
of the IEEE International Conference on Robotics and
Automation, New Orleans, April 2003, pp. 636-642.
[3] J. Borenstein and H. R. Everett, “Navigating Mobile Ro-
bots: Sensors and Techniques,” A. K. Peters Ltd., Welles-
ley, 1992.
[4] Q. Li, M. D. Rosa and D. Rus, “Distributed Algorithms
for Guiding Navigation across a Sensor Network,” Pro-
ceedings of the 9th Annual International Conference on
Mobile Computing and Networking, San Diego, 2003, pp.
313-325.
[5] A. J. Briggs, C. Detweiler, D. Scharstein and A. Vanden-
berg-Rodes, “Expected Shortest Paths for Landmark-
Based Robot Navigation,” International Journal of Ro-
botics Research, Vol. 23, No. 7-8, July 2004, pp. 717-728.
doi:10.1177/0278364904045467
[6] A. Verma, H. Sawant, J. Tan, “Selection and Navigation
of Mobile Sensor Nodes Using a Sensor Network,” Pro-
ceedings of Third IEEE International Conference on Per-
vasive Computing and Communications, Pisa, March
2005, pp. 41-50.
[7] J. Borenstein and Y. Koren, “The Vector Field Histo-
gram-Fast Obstacle Avoidance for Mobile Robots,” IEEE
Journal of Robotics and Automation, Vol. 7, No. 3, 1991,
pp. 278-288. doi:10.1109/70.88137
[8] J. Liu, J. Liu, M. Chu, J. E. Reich and F. Zhao, “Distrib-
uted State Representation for Tracking Problems in Sen-
sor Networks,” Proceedings of third Workshop on Infor-
mation Processing in Sensor Networks (IPSN), New York,
April 2004, pp. 234-242.doi:10.1145/984622.984657
[9] J. Liu, J. Liu, J. Reich, P. Cheung and F. Zhao, “Distrib-
uted Group Management for Track Initiation and Main-
tenance in Target Localization Applications,” Proceed-
ings of 2nd workshop on Information Processing in Sensor
Networks (IPSN), Berlin, April 2003, pp. 113-128.
[10] S. Meguerdichian, F. Koushanfar, G. Qu and I. Potkonjak,
“Exposure in Wireless Ad-Hoc Sensor Networks,” Pro-
ceedings of 7th Annual International Conference on Mo-
bile Computing and Networking, New York, July 2001,
pp. 139-150.
[11] S. Oh, L. Schenato and S. Sastry, “A Hierarchical Multi-
ple-Target Tracking Algorithm for Sensor Networks,”
Proceedings of the International Conference on Robotics
and Automation, Barcelona, April 2005, pp. 2197- 2202.
[12] L. Schenato, S. Oh, P. Bose and S. Sastry, “Swarm Coor-
dination for Pursuit Evasion Games Using Sensor Net-
works,” Proceedings of the International Conference on
Robotics and Automation, Padova, April 2005, pp. 2493-
2498. doi:10.1109/ROBOT.2005.1570487
[13] J. P. Hespanha, H. J. Kim and S. S. Sastry, “Multi-
ple-Agent Probabilistic Pursuit-Evasion Games,” Pro-
ceedings of the IEEE International Conference on Deci-
sion and Control, Phoenix, 1999, pp. 2432-2437.