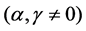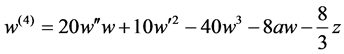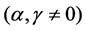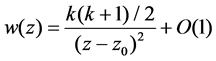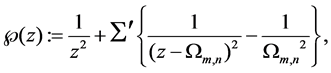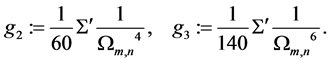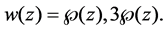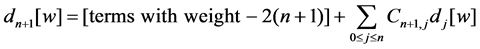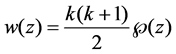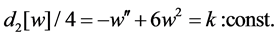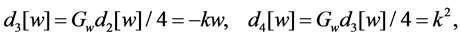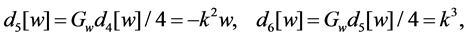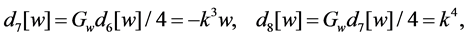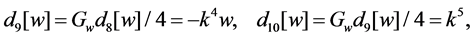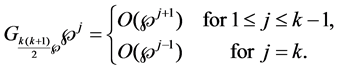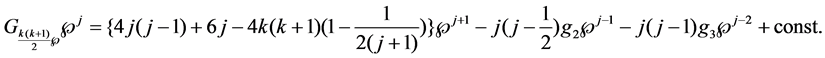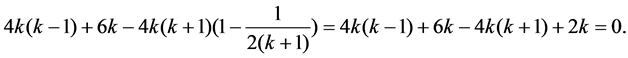Journal of Applied Mathematics and Physics
Vol.04 No.04(2016), Article ID:66587,6 pages
10.4236/jamp.2016.44093
Weierstrass’ Elliptic Function Solutions to the Autonomous Limit of the String Equation
Yoshikatsu Sasaki
Department of Mathematics, Hiroshima University, Higashi-Hiroshima, Japan



Received 4 January 2016; accepted 23 April 2016; published 30 April 2016
ABSTRACT
In this article, we study the string equation of type (2, 2n + 1), which is derived from 2D gravity theory or the string theory. We consider the equation as a 2n-th order analogue of the first Painlevéequation, take the autonomous limit, and solve it concretely by use of the Weierstrass’ elliptic function.
Keywords:
Painlevé Hierarchy, String Equation, Elliptic Function

1. Introduction
1.1. The String Equation of Type (2, 2n + 1)
Let 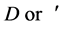 stand for the differentiation w.r.t.
stand for the differentiation w.r.t.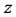 , and
, and 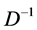 stand for the inverse operator of
stand for the inverse operator of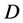 . Consider the commutator equation of ordinary differential operators
. Consider the commutator equation of ordinary differential operators
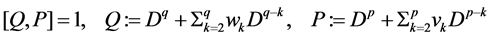 (1)
(1)
for a couple of positive integers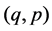 . The above equation is called the string Equation (or Douglas equation) of type
. The above equation is called the string Equation (or Douglas equation) of type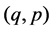 , and appears in the string theory or the theory of 2D quantum gravity [1]-[8]. In the followings, we set
, and appears in the string theory or the theory of 2D quantum gravity [1]-[8]. In the followings, we set 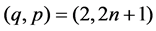 for a positive integer
for a positive integer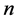 .
.
In the case where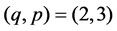 , the string equation is written as an ODE satisfied by the potential
, the string equation is written as an ODE satisfied by the potential 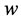 of Sturm-Liouville operator
of Sturm-Liouville operator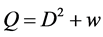 , and then, by a fractional linear transformation, it is reduced to the first Painlevé equation [9]-[11]. In fact, the string equation of type
, and then, by a fractional linear transformation, it is reduced to the first Painlevé equation [9]-[11]. In fact, the string equation of type 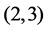
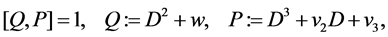 (2)
(2)
i.e.
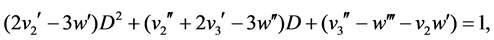 (3)
(3)
is written as an equation 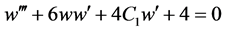 or integrated one
or integrated one 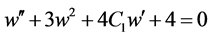 with integral constants
with integral constants 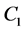
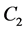
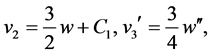
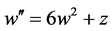
by replacement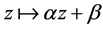
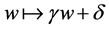
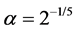
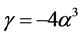
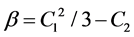
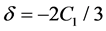
In the case where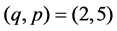
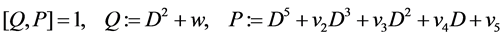
is similarly reduced to
by replacement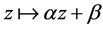
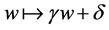
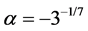
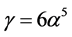
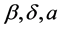
1.2. The First Painlevé Hierarchy
Now we recall the definition of the first Painlevé hierarchy. Consider the serial equations
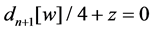
for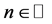

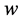
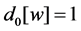
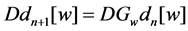
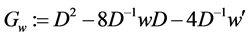
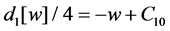
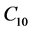
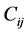
If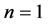
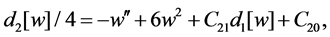
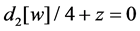
If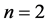
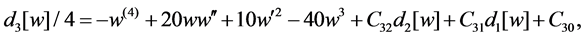
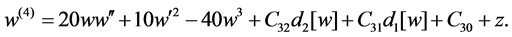
Again, it essentially coinsides with (5), i.e. the 4th order equation of the first Painlevé hierarchy.
As proved by K. Takasaki [8], the string equation of type 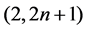
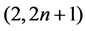
Note that S. Shimomura [14] proved the theorems as follows.
Theorem A [14]. Each 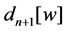
Theorem B [14]. At each pole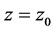
for some positive integer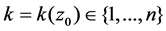
The author proved a theorem similar to Theorem A for the second Painlevé hierarchy [15], and, in its proof, auxiliary differential polynomials play important roles. So, for the first Painlevé hierarchy as well, the auxiliary differential polynomials should exist. Recall them.
Theorem C [16]. Define 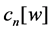
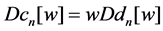
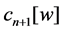
1.3. Autonomous Limits
The first Painlevé equation has the autonomous limit [9]. Replacing 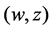
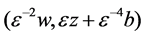
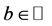
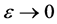
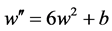
where 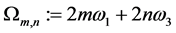
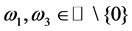
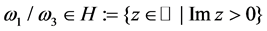
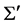
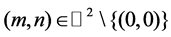
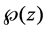
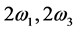
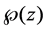
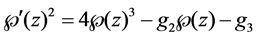
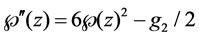
where
For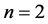
Theorem D [17]. The 4th order equation of the first Painlevé hierarchy with suitable parameters
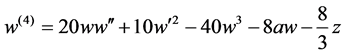
is reduced to the autonomous equation
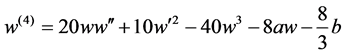
by replacing 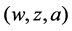
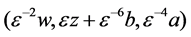
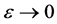
Note that the Equation (8) is obtained as a section of the most degenerated 2D Garnier system [18] (see also [19] [20]). The following theorem is not trivial but natural if we consider Theorem D together with Theorem B.
Theorem E [17]. For suitable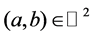
1.4. Results
A result similar to Theorem D is valid for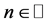
Theorem 1.1. The autonomous limit of the string equation of type 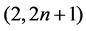
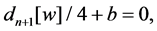
where 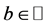
Proof. Note that 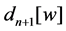
with the weight [14] 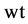
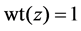
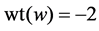
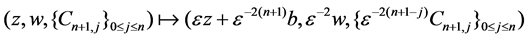
taking the limit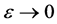
For the autonomous limit Equation (10), each auxiliary differential polynomial obtained in Theorem C has clear meaning.
Theorem 1.2. The differential polynomial 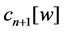
Proof. By definition,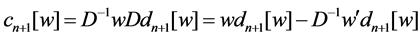
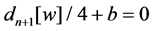
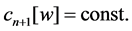
Now we extend Theorem E to the case where
Theorem 1.3. Weierstrass’ elliptic function 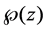
Moreover, we can prove the theorem as follows:
Theorem 1.4. For each integer 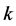
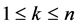
is a solution to (10) with suitable parameters.
The proofs of these two theorems are given in the next section.
2. Proofs of Theorem 1.3 and 1.4
2.1. Proof of Theorem 1.3
Let all of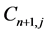
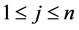
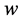
with suitable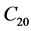
with suitable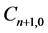
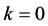
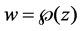
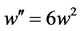
2.2. Proof of Theorem 1.4
Theorem 1.4 immediately follows from the following lemma.
Lemma. For every positive integer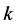
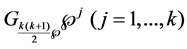
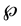
Proof. Using 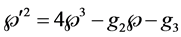
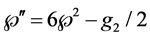
So, if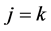
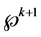
Thus, we have
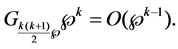
Note that 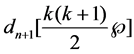
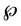
3. Discussion
The results of this article are summarized as follows: we obtained the autonomous limit of the string equation of type 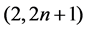
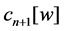
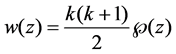
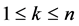
Of course, poles of these solutions are uniform, i.e. every pole 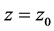
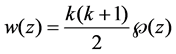
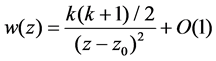
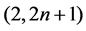
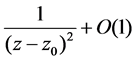
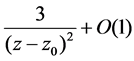
Another remark should be given. T. Oshima and H. Sekiguchi [21] studied the commutator equation 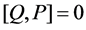

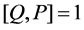
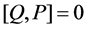
implies that, in view of the string theory, the first Painlevé equation is not only a nonautonomization but also a quantization of the Weierstrass’ elliptic function. Relation between their solutions and our special solutions should be studied in the future. It may yield a new kind of quantization of KdV equation or hierarchy. Autonomous limit is a kind of approximation of the differential equation. Therefore, the solutions of the autonomous limit equation gives us information on the asymptotics of the nonautonomous equation, as well as does on the first Painlevé equation. Moreover, if all of the solutions to the autonomous limit equation are determined, it contributes the argument on the irreducibility of the string equation in the sence of the differential Galois theory, as well as on the irreduciblity of the first Painlevé equation.
Acknowledgements
The author wishes to acknowledge Prof. T. Oshima for his helpful comment.
Cite this paper
Yoshikatsu Sasaki, (2016) Weierstrass’ Elliptic Function Solutions to the Autonomous Limit of the String Equation. Journal of Applied Mathematics and Physics,04,857-862. doi: 10.4236/jamp.2016.44093
References
- 1. Adler, M. and van Moerbeke, P. (1992) A Matrix Integral Solution to Two-Dimensional Wp-Gravity. Comm. Math. Phys., 147, 25-26. http://dx.doi.org/10.1007/BF02099527
- 2. Douglas, M.R. (1990) String in Less than One-Dimensions and KdV Hierarchies. Phys. Lett. B, 238, 176-180. http://dx.doi.org/10.1016/0370-2693(90)91716-O
- 3. Fukuma, M., Kawai, H. and Nakayama, R. (1991) Infinite Dimen-sional Grassmannian Structure of Two Dimensional String Theory. Comm. Math. Phys., 143, 371-403. http://dx.doi.org/10.1007/BF02099014
- 4. Kac, V. and Schwarz, A. (1991) Geometric Interpretation of Partition Functions of 2D Gravity. Phys. Lett. B, 257, 329- 334. http://dx.doi.org/10.1016/0370-2693(91)91901-7
- 5. vanMoerbeke, P. (1994) Integrable Foudations of String Theory. In: Babelon, O., et al., Eds., Lectures on Integrable Systems, World Sci. Publ., Sin-gapore, River Edge, 163-267.
- 6. Moore, G. (1990) Geometry of the String Equations. Comm. Math. Phys., 133, 261-304. Matrix Models of 2D Gravity and Isomonodromic Deformations. Prog. Theor. Phys. Suppl., 102, 255-285. http://dx.doi.org/10.1143/PTPS.102.255
- 7. Schwarz, A. (1991) On Solutions to the String Equations. Mod. Phys. Lett. A, 29, 2713-2725. http://dx.doi.org/10.1142/S0217732391003171
- 8. Takasaki, K. (2007) Hamiltonian Structure of PI Hierarchy. SIGMA, 3, 42-116. http://dx.doi.org/10.3842/sigma.2007.042
- 9. Conte, R. and Mussette, M. (2008) The Painlevé Handbook. Springer Science + Business Media B.V., Dordrecht.
- 10. Gromak, V.I., Laine, I. and Shimomura, S. (2002) Painlevé Differential Equations in the Complex Plane. Walter de Gruyter, Berlin, New York. http://dx.doi.org/10.1515/9783110198096
- 11. Ince, E.L. (1956) Ordinary Differential Equations. Dover Publ., New York.
- 12. Kudryashov, N.A. (1997) The First and Second Painlevé Equations of Higher Order and Some Relations between Them. Phys. Lett. A, 224, 353-360. http://dx.doi.org/10.1016/S0375-9601(96)00795-5
- 13. Weiss, J. (1984) On Classes of Integrable Systems and the Painlevé Property. J. Math. Phys., 25, 13-24. http://dx.doi.org/10.1063/1.526009
- 14. Shimomura, S. (2004) Poles and α-Points of Meromorphic Solutions of the First Painlevé Hierarchy. Publ. RIMS, Kyoto Univ., 40, 471-485. http://dx.doi.org/10.2977/prims/1145475811
- 15. Sasaki, Y. (2013) Lower Estimates of the Growth Order of Solutions to the Second Painlevé Hierarchy. J. Math. Phys., 54, 073510.
- 16. Sasaki, Y. (2015) Auxiliary Differential Polynomials for the First Painlevé Hierarchy. Proc. Japan Acad., Ser. A, 91, 7-8. http://dx.doi.org/10.3792/pjaa.91.7
- 17. Sasaki, Y. (2014) Weierstrass’ Elliptic Function Solution to the Auto-nomous Limit of the String Equation of Type (2,5). Adv. Pure Math., 4, 494-497. Erratum to “Weierstrass’ Elliptic Function Solution to the Autonomous Limit of the String Equation of Type (2,5)”. [Advances in Pure Mathematics 4 (2014), 494-497], ibid., 680-681.
- 18. Shimomura, S. (2000) Painlevé Property of a Degenerate Garnier System of (9/2)-Type and a Certain Fourth Order Non-Linear Ordinary Differential Equation. Ann Scuola Norm. Sup. Pisa Cl. Sci., XXIX, 1-17.
- 19. Kimura, H. (1989) The Degeneration of the Two Dimensional Garnier System and the Polynomial Hamiltonian Structure. Ann.Mat. Pura. Appl., 155, 25-74. http://dx.doi.org/10.1007/BF01765933
- 20. Suzuki, M. (2006) Spaces of Initial Conditions of Garnier System and Its Degenerate Systems in Two Variables. J. Math. Soc. Japan, 58, 1079-1117. http://dx.doi.org/10.2969/jmsj/1179759538
- 21. Oshima, T. and Sekiguchi, H. (1995) Commuting Families of Differential Operators Invariant under the Action of a Weyl Group. J. Math. Sci. Univ. Tokyo, 2, 1-75.
- 22. Adler, M. and van Moerbeke, P. (1992) A Matrix Integral Solution to Two-Dimensional Wp-Gravity. Comm. Math. Phys., 147, 25-26. http://dx.doi.org/10.1007/BF02099527
- 23. Douglas, M.R. (1990) String in Less than One-Dimensions and KdV Hierarchies. Phys. Lett. B, 238, 176-180. http://dx.doi.org/10.1016/0370-2693(90)91716-O
- 24. Fukuma, M., Kawai, H. and Nakayama, R. (1991) Infinite Dimen-sional Grassmannian Structure of Two Dimensional String Theory. Comm. Math. Phys., 143, 371-403. http://dx.doi.org/10.1007/BF02099014
- 25. Kac, V. and Schwarz, A. (1991) Geometric Interpretation of Partition Functions of 2D Gravity. Phys. Lett. B, 257, 329- 334. http://dx.doi.org/10.1016/0370-2693(91)91901-7
- 26. vanMoerbeke, P. (1994) Integrable Foudations of String Theory. In: Babelon, O., et al., Eds., Lectures on Integrable Systems, World Sci. Publ., Sin-gapore, River Edge, 163-267.
- 27. Moore, G. (1990) Geometry of the String Equations. Comm. Math. Phys., 133, 261-304. Matrix Models of 2D Gravity and Isomonodromic Deformations. Prog. Theor. Phys. Suppl., 102, 255-285. http://dx.doi.org/10.1143/PTPS.102.255
- 28. Schwarz, A. (1991) On Solutions to the String Equations. Mod. Phys. Lett. A, 29, 2713-2725. http://dx.doi.org/10.1142/S0217732391003171
- 29. Takasaki, K. (2007) Hamiltonian Structure of PI Hierarchy. SIGMA, 3, 42-116. http://dx.doi.org/10.3842/sigma.2007.042
- 30. Conte, R. and Mussette, M. (2008) The Painlevé Handbook. Springer Science + Business Media B.V., Dordrecht.
- 31. Gromak, V.I., Laine, I. and Shimomura, S. (2002) Painlevé Differential Equations in the Complex Plane. Walter de Gruyter, Berlin, New York. http://dx.doi.org/10.1515/9783110198096
- 32. Ince, E.L. (1956) Ordinary Differential Equations. Dover Publ., New York.
- 33. Kudryashov, N.A. (1997) The First and Second Painlevé Equations of Higher Order and Some Relations between Them. Phys. Lett. A, 224, 353-360. http://dx.doi.org/10.1016/S0375-9601(96)00795-5
- 34. Weiss, J. (1984) On Classes of Integrable Systems and the Painlevé Property. J. Math. Phys., 25, 13-24. http://dx.doi.org/10.1063/1.526009
- 35. Shimomura, S. (2004) Poles and α-Points of Meromorphic Solutions of the First Painlevé Hierarchy. Publ. RIMS, Kyoto Univ., 40, 471-485. http://dx.doi.org/10.2977/prims/1145475811
- 36. Sasaki, Y. (2013) Lower Estimates of the Growth Order of Solutions to the Second Painlevé Hierarchy. J. Math. Phys., 54, 073510.
- 37. Sasaki, Y. (2015) Auxiliary Differential Polynomials for the First Painlevé Hierarchy. Proc. Japan Acad., Ser. A, 91, 7-8. http://dx.doi.org/10.3792/pjaa.91.7
- 38. Sasaki, Y. (2014) Weierstrass’ Elliptic Function Solution to the Auto-nomous Limit of the String Equation of Type (2,5). Adv. Pure Math., 4, 494-497. Erratum to “Weierstrass’ Elliptic Function Solution to the Autonomous Limit of the String Equation of Type (2,5)”. [Advances in Pure Mathematics 4 (2014), 494-497], ibid., 680-681.
- 39. Shimomura, S. (2000) Painlevé Property of a Degenerate Garnier System of (9/2)-Type and a Certain Fourth Order Non-Linear Ordinary Differential Equation. Ann Scuola Norm. Sup. Pisa Cl. Sci., XXIX, 1-17.
- 40. Kimura, H. (1989) The Degeneration of the Two Dimensional Garnier System and the Polynomial Hamiltonian Structure. Ann.Mat. Pura. Appl., 155, 25-74. http://dx.doi.org/10.1007/BF01765933
- 41. Suzuki, M. (2006) Spaces of Initial Conditions of Garnier System and Its Degenerate Systems in Two Variables. J. Math. Soc. Japan, 58, 1079-1117. http://dx.doi.org/10.2969/jmsj/1179759538
- 42. Oshima, T. and Sekiguchi, H. (1995) Commuting Families of Differential Operators Invariant under the Action of a Weyl Group. J. Math. Sci. Univ. Tokyo, 2, 1-75.