 Circuits and Systems, 2016, 7, 735-747 Published Online May 2016 in SciRes. http://www.scirp.org/journal/cs http://dx.doi.org/10.4236/cs.2016.76063 How to cite this paper: Rajeswari, D. and Senthilkumar, V.J. (2016) Minimizing Time in Scheduling of Independent Tasks Using Distance-Based Pareto Genetic Algorithm Based on MapReduce Model. Circuits and Systems, 7, 735-747. http://dx.doi.org/10.4236/cs.2016.76063 Minimizing Time in Scheduling of Independent Tasks Using Distance-Based Pareto Genetic Algorithm Based on MapReduce Model Devarajan Rajeswari*, Veerabadran Jawahar Senthilkumar Department of Electronics and Communication Engineering, College of Engineering, Anna University, Chennai, India Received 21 March 2016; accepted 9 May 2016; published 12 May 2016 Copyright © 2016 by authors and Scientific Research Publishing Inc. This work is licensed under the Creative Commons Attribution International License (CC BY). http://creativ ecommon s.org/l icenses/by /4.0/ Abstract Distributed Systems (DS) have a collection of heterogeneous computing resources to process user tasks. Task scheduling in DS has become prime research case, not only due of finding an optimal schedule, but also because of the time taken to find the optimal schedule. The users of Ds services are more attentive about time to complete their task. Several algorithms are implemented to find the optimal schedule. Evolutionary kind of algorithms is one of the best, but the time taken to find the optimal schedule is more. This paper presents a distance-based Pareto genetic algorithm (DPGA) with the Map Reduce model for scheduling independent tasks in a DS environment. In DS, most of the task scheduling problem is formulated as multi-objective optimization problem. This paper aims to develop the optimal schedules by minimizing makespan and flow time simultaneously. The algorithm is tested on a set of benchmark instances. MapReduce model is used to parallelize the execution of DPGA automatically. Experimental results show that DPGA with MapReduce mod- el achieves a reduction in makespan, mean flow time and execution time by 12%, 14% and 13% than non-dominated sorting genetic algorithm (NSGA-II) with MapReduce model is also imple- mented in this paper. Keywords Distributed Systems, Multi-O bjective, MapReduce, Opti mization , DPGA, NSGA-II *  D. Rajeswari, V. J. Senthilkumar 1. Introduction The Computationa l power of individ ual system is not suf ficient for solving widel y used complex co mputatio nal tasks like high energy physics, earth science, etc. In order to solve complex jobs, high performance parallel and distributed systems are developed with a number of processors. As the computing nodes are heterogeneous in a multiprocessor environment, execution time of tasks varies on each processor. Scheduling of tasks is a key issue, to achieve the high usability of supercomputing capacity of distributed computing environment [1]. To ensure efficient utilization of resources, suitable scheduling algorithms are used to assign the tasks to the available pro- cessors efficiently. For distributed computing environment, static scheduling can be used due to geographically distributed com- puting resources with various ownerships, access policy and different constraints. Schedulers are developed us- ing complex arithmetic techniques that use the available values of application and environment. So, heuristic methods are the best approach to find the optimal schedule in the DS enviro nment [2]. The most important crite- ria used to analyze the efficiency of scheduling techniques are makespan and flowtime. Time taken to complete the last task is Makespan [3] and the sum of completion time of all tasks in a schedule is flowtime. The sche- dule, which optimizes the makespan and flowtime is called as optimum schedule [4]. To minimize makespan, the Longest Job to be scheduled to Fastest Resource (LJFR) and for minimizing flowtime, the Shortest Job to be scheduled to Fastest Resource (LJFR) [2]. Flowtime minimization makes the makespan maximization. This leads the pro blem as multiple o bjective. Genetic Algorithm (GA) is a search and population-based model [5]. This has b een exte nsivel y used i n vari- ous problem domains. GA has the capability to search various regions of the solution space and note a diverse set of solutions for the distributed computing problem. GA uses genetic operators to improve the structure of good solutions in various objective spaces. These characteristics of GA used to find the best optimal schedule for multi-objective problem in distributed systems. The distance-based Pareto genetic algorithm (DPGA) of Osyczka [6] is used in this paper. DPGA uses a distance computation and dominance test procedure and elitist method of combining parent populatio n with the of fspring po pulation for t he next iteratio n. Set of most d ifficult static benchmark instances of Braun et al. [1] is used to analyze the performance of NSGA-II. The degree of task and resource heterogeneity can be captured by these instances. Hadoop MapReduce is a framework for dis- tributed large scale data processing on computer clusters. MapReduce is used to automatically parallelize the data processing on clusters in a reliable and fault-tolerant manne r [7]. MapReduce programming model is used to implement the multi-objective DP GA to find the o pti mal schedule with minimum time in the distributed computing environment. The DPGA with MapReduce model suits for dis- tributed computing environments with various co mputing resources and scheduling is done by considering ma- kespan and flowtime minimization. The DPGA with MapReduce model generates better solutions in minimal time than N SGA-II with MapReduce model. The remainder of the paper is structured as follows. Section 2 discusses t he literature revie w. Multi-objective optimization introduction is presented in Section 3. Section 4 determines for identifying the variety of distri- buted c o mput i n g e nvir o n me nt in t he s i mula t io n p r oc e ss. A Sc hed ul in g method usi n g NSGA-II with MapReduce and DPGA with MapReduce is available in Section 5. Simulation results are shown in Section 6. Finally, Sec- tion 7 concludes and discu s s es the future work. 2. Related Work Optimal scheduling of independent tasks to available resources in DS is an NP-complete problem and it depends on var ious heur istics a nd meta -heuristic algorithms. A fe w well kno wn heur istic metho ds ar e min-max [8], suf- frage [9], min-min, max -min [10] and LJFR-SJFR [11]. These above heuristic methods are more time consum- ing process. In recent, several meta-heuristic methods are developed to solve complex computational problems. The most popular methods are GA [6], particle swarm optimizatio n (PSO) [12], ant colony opti mization (ACO) [13] and simulate d a nneal in g ( SA) [14]. The description of eleven heur isti cs a nd co mpar i son o n the va rio us d is- tributed environment was done by Braun et al. [1] and illustrates the effectiveness of GA with others. All the above meta-heuristic methods considered single objective and aimed to minimize the makespan. There are some methods considered multiple objectives, while scheduling tasks in distributed environments. Izakian et al. [15] compares five heuristics depends on the machine, and task characteristics for minimizing both makespan and flowtime, but calculated separately. Several nature inspired meta-heuristic methods like GA,  D. Rajeswari, V. J. Senthilkumar ACO and SA for scheduling tasks in a grid computing environment by using single and multi-objective optimi- zati on wa s done b y Abr aham et al. [16]. Xhafa et al. [17] implemented GA based sched uler. All the above me- thods convert the multi-objective optimization problem into a scalar cost function, which makes single objective before optimization. To minimize the amount of ti me to find the best op timal schedule Li m et al. [18] implemented PGA, Durillo et al. [19] implemented p arallel execution of NSG A-II and these methods have the d ifficulties to make co mmu- nication and synchronization between the resources in a distributed environment. This paper implements NSGA-II with MapReduce programming model and DPGA with MapReduce programming model to find the best optimal schedule. It makes the task scheduling as an efficient real time multi-objective optimization prob- lem. 3. Multi-Objective Optimization The Scheduling problem in a distributed environment needs to optimize the several objectives at the same time. In general, these objectives are contradictory with each other. These contradictory objective functions generates a set of optimal sol utions. I n the opti mal solution se t, not one so lution is greate r than eac h another sol ution with regarding all the o bjective functions. T hese opti mal solution set is called as Pareto optimal solution. T he multi- objective minimization problem is formulated as, ( )( )( ) ( ) 12 Minimize ,,, subject to m zgagagaa s= ∈ (1) where is the vector of decision variables, , is the objective functions a nd is the suitable region in the decision space. A result is said to do minate another resul t , if the subse quent things are satisfied, {}()( ) {}()( ) 1,2,,, 1,2,,, kk kk kmga gb kmga gb ∀∈ ≤ ∃∈ < (2) a is said to be a Pareto optimal solution, where no solution dominates . The b e st solution of the Pareto op- timal set is called as a Pareto optimal front in multi objective problem space. Once the entire Pareto optimal so- lution is found, that is the indication of completin g multi-objective problem [20]. Multi objective optimization is also known as vector optimization, as a vector of objectives is optimized in- stead of a single objective. When using multiple objectives, the search space is divided into two non overlapping regions kno wn as opti mal and non-optimal. The difference between single objective and multiple objective op- timization are handling two search spaces and having two goals instead of single. 4. Problem Statement Distributed environment has geographically distributed computing systems with complex combinations of hardware, software and network components. R is the set of m processing elements in distributed environment and T is the set of n tasks assigned to the processing elements. As scheduling is performed for independent tasks, there is no communication among the tasks and a task can be assigned to a processing element exclusively. The pre-emption of task is not allowed. As scheduling is performed statically, computing capacity and prior load of processing ele ment and co mp utational load o f the tas k is estimated a nd the tasks are sc heduled in batc hes, once allocated the tasks it cannot be migrated to another resource. Expected time to compute matrix (ETC) can be built by usin g these details. An ET C matrix is a p × q matrix, in which eac h position of t he matrix, ET C [p] [q] illustrates the expected time to co mplete job p in resource q. The row of ETC matrix has the completion time of a job of each resource and each column specifies the estimated execution time of a resource for all the jobs. Hence, the proposed method is static, non-pre e mpti ve sc heduli ng. In this paper, the objective considered is minimization of makespan and flow time. Make span is the comple- tion time and waiting time of a task in a processing element. Flow time is defined as the sum of completion time of all the tasks de scribed as follows, { } min max j sScht taskst makespan F ∈∈ = (3)  D. Rajeswari, V. J. Senthilkumar { } min j sSchttaskst flowtime F ∈∈ = ∑ (4) whe re the completion time of task t, tasks stands for a set of all tasks, Sch is se t of all possible schedules. Longest job has to be scheduled on fastest resource to minimize the makespan and for minimizing flow time, shortest job to be scheduled on fastest resources. This contradiction makes the problem as multi-objective. 5. Multi-Objective GA with MapReduce for Scheduling Tasks to the Distributed Environment 5.1. Elitist Non-Dominated Sorting Genetic Algorithm (NSGA-II) Initial populations of size N are generated randomly. Non-dominated sorting is performed on the population to classify it into a number of fronts. Crowded tournament selection is performed by assigning crowding distance. This is used to select a better ranked solution if they belong to differe nt front or select the higher crowding distance sol ution i f the y belo ng to same front. Crosso ver and mutat ion are per formed o n the generated parent solutio n and produce the offspring with size N. Single point crossover and swap mutation is used. The parent and offspring population of size N are combined and produce 2N population. Upd ate the populati on by the indivi duals fr om low- er front to size n. The indi vidual has small cro wding dis tance will be dropped in t he tie. Precede again, except the first step till meets the stopping criteria [21]. Figure 1 shows the workflow of NSGA-II with MapReduce model. Non-dominated sorting: It is used to find the individuals to the next iteration by classifying the population. The proc edure is given below [22]. Step 1: For ind ivid ual solution p in population N. Step 2: For ind ivid ual solution q in population N. Step 3: If p and q are not equal, Compare p and q for all the objectives. Step 4: For any p, q is dominated by p, mark solution q as dominated. First non-dominated set is formed from unmarked solutions. Step 5: Repe at the procedure till the entire pop ulation is divided into fronts. Selection: The Crowded tournament selection operator is used. An individual i win the tournament with another i ndividual j, if one of t he following is true [22]. 1. An individual i have better rank, i.e ., ra nki < rankj. 2. T he ind ividua l i and j have the sa me ran k (r anki = r ankj ), then t he i ndivid ua l i has b ette r cr owdin g dist anc e (in less crowded areas, i.e., di = dj) than individual j. Crow ding dista nce calcula tion: To break the tie between the individuals are having the same rank crowding distance is used [22]. The procedure is as follows, Step 1: Initialize the number of indi vid uals (x) in the front (Fa). Step 2: Set the crowding dista nce di = 0, . Step 3: Sort the individuals (x) in front (Fa) based on the objective function (obj). obj = . m is the number of objectives and S = sort (Fa, obj). Step 4: Set the distance of boundary individuals as S(d1) = ∞ and S(dx) = ∞. Step 5: Set k = 2 to (x-1) and calculate S(d2) = S(dx-1) as follows ( ) ( ) ( )( ) max min 11 mm m kk mm SkfSkf Sd Sdff + −− = +− (5) is the kth indi vidua l value in S for mth objecti ve function. 5.2. Distance-Based Pareto Genetic Algorithm (DPGA) At first distance-based fitness assignment was proposed by Osyczka and Kundu [6], the idea gi ving impor tance to b o th P a re to op timal fr o nt a nd the d i ver si t y of t ha t fr o nt i n o ne fitnes s mea sur e. DP GA use s a d ist a nce compu- tation and dominance test procedure with complexity O (kη2) [4]. DPGA maintains a standard GA population and Elite population. The genetic operations like selection, crossover and mutation are performed on GA popu- lation. All the non-dominated solutions are maintained in elite p opulation. T he step s are as follows [23]: Step 1: Initialize the r ando m pop ulation of size N (P0) 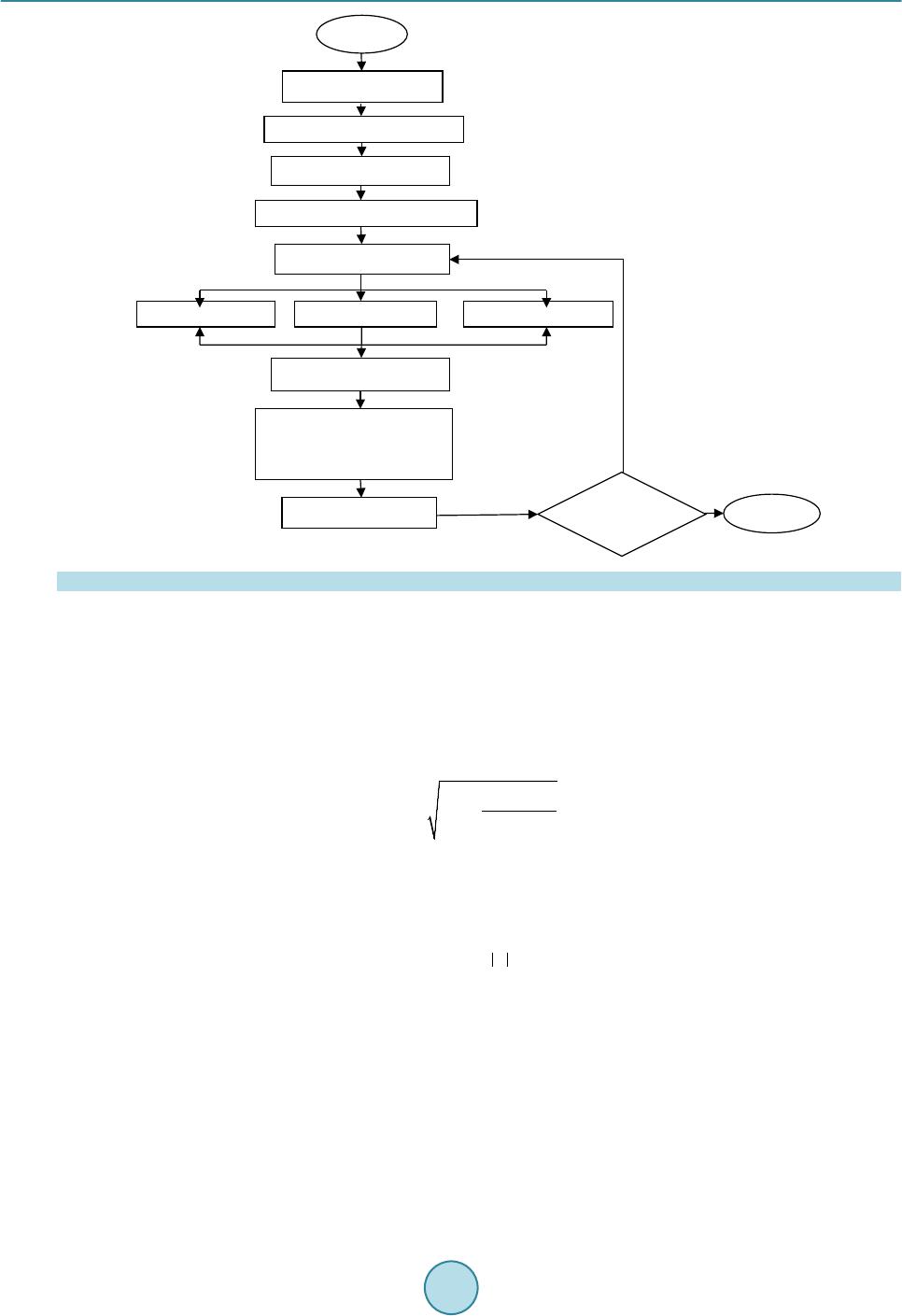 D. Rajeswari, V. J. Senthilkumar Figure 1. F lo wc hart for NSGA-II with MapReduce. Step 2: Calculate the fitness for the first solution (F1) and set generation counter c = 0. Step 3: If c = 0, insert the first element of P0 in the elite set E0 and perform the distance calculation, mini- mum distance, index of elite member, elite population updating for each member of the population (k≥2) and k≥1 for c > 0. 3a. Distance Calculation Distance calculation is to find the distance between population member and elite member in the objective space [23]. The formula for calculating distance is given belo w: ( )() ( ) 1 ik M imm ki mm ef de = − = ∑ (6) em is the fitness of elite member, fm is the fitness o f population member for particular objectives. 3b. Minimum Distance Calculation Find the minimu m distance o f a population member co mpared to all the member of an elite set [23]. It is cal- culated as follows, (7) E is an elite set, dk is the calculated distance. 3c. Elite member ind ex The Elite member index is used to find which member of elite set has near to the member of the population [23]. (8) is the calculated distance and is the minimum distance. 3d. Fitness Calculation and Elite set up date The elite set is updated depends on the domination of population member [23]. Population member (k) is Map phase Reduce phase … No Start Initialize pop ulation Fitness function evaluation Non-dominated sorting Crowded tournament selection Crossover and mutation Fitness evaluation Select N individuals Stopping criteria? Stop Combine parent and child populat ion, non-dominated sorting Fitness evaluationFitness evaluation Coordinator Aggregate fitness va lue Coordinator 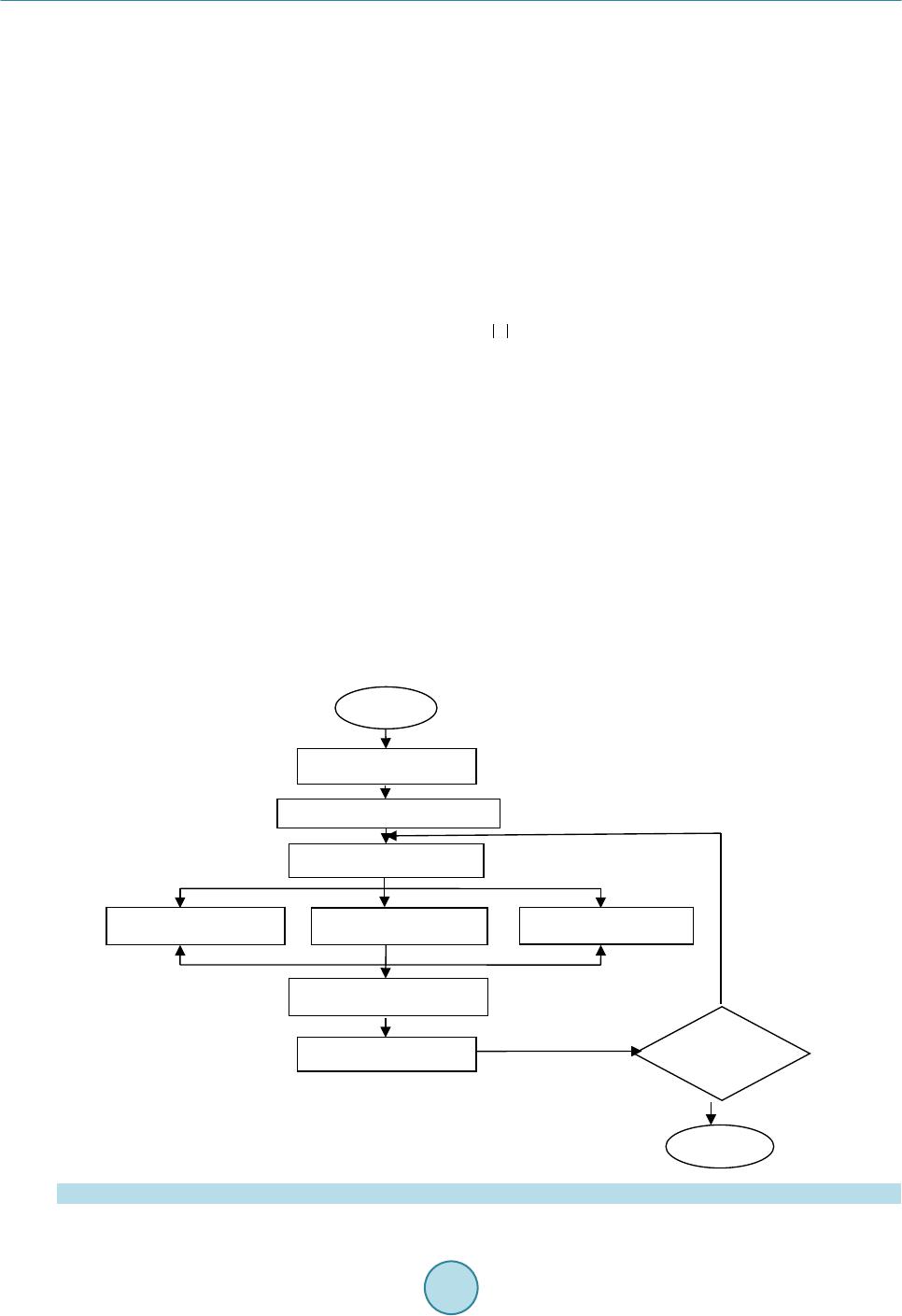 D. Rajeswari, V. J. Senthilkumar dominated by elite solution, th e fitness of k is () *min max 0,k i k FFe d = − (9) Oth er wi s e (10) and the population member is incl ud e d by eliminatin g all d ominated elite members in elite set. Step 4: Find the minimum fitness value among all the members of elite population and all elite solutions are assigned fit ness Fmin. 4a. Minimum fitnes s Minimum fitness is used to find minimum fitness value among all the members of elite population and all elite solutions are a ssigned a fitnes s Fmin [23] is, (11) E is elite set; F is the fit ness of elite solution. Step 5: Stop c + 1 = cmax or ter mination criterion i s satisfied. Otherwise, go to step 6. Step 6: Generate new population (Pc+1) by using selection, crossover and mutation on Pc. Set c = c + 1 and go to step 3. There is no genetic operations like reproduction, crossover and mutation is performed on elite population Ec explicitly. To generate the new population selection, crossover and mutation operators are used. In this paper, tournament selection, single point crossover and swap mutation are used. Figure 2 shows the workflow of DPGA with MapReduce model. 5.3. MapReduce Model Hadoop: Hadoop is an open source framework that provides reliable, scalable, distributed processing and storage on large clusters of inexpensive servers [24]. Hadoop is written in Java and users can customize the code to parallelize the data process in clusters which contains thousands of commodity servers. The response time Figure 2. Flowchart for DPGA with MapReduce. … Yes Map phase Reduce phase No Coordinator Coordinator Start Initialize pop ulation Fitness function evaluation Crossover and mutation Fitness assignment Stopping criteria? Stop Minimum fitness Fitness assignmentFitness assignment Aggregate fitness va lue 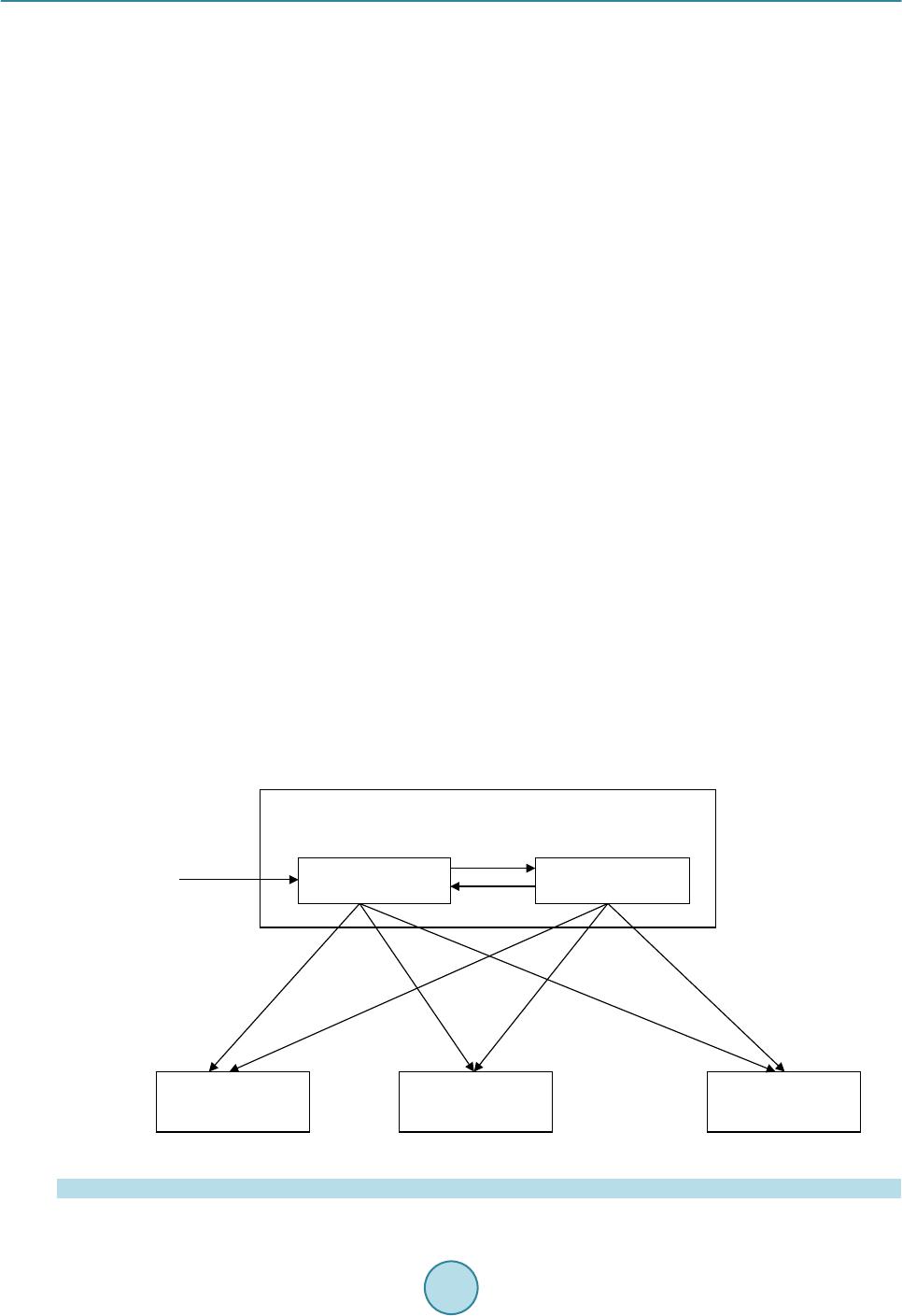 D. Rajeswari, V. J. Senthilkumar depends on the complexity of process and volumes of data. The advantage of Hadoop is its massive scalability. The Apache Hadoop framework consists of Hadoop kernel, MapReduce, Hadoop Distributed File System (HDFS) and some related projects like HBase, Hive and Zookeeper. At present, Hadoop plays a major role in Email spa m detection, search engines, ge nome manipulatio n in life scie nces, advertisin g, predic tion in financ ial service and analysis of log files. Linux and Windows are a preferred operating system for Hadoop. HDFS: A file system component of Had oop is called a s HDFS. Distributed low-cost hardware is used to store data in HDFS.HDFS contains name node and data node. A name node has Meta data information. If there is a request to read a data from HDFS, the name node provides the location of data blocks. The name node also has overall system information. So the name node is called as master of HDFS. The secondary name node has the replication of Meta data. At first, data node has to be registered in name node and gets namespace ID. For every particular period of time, the data node updates its status to name node. HDFS splits the large file into blocks and stor ed it in the different data nodes. Each block is replicated at the nodes of Hadoop cluster. At the time of failure data is re-replicated b y the active Hadoop monitoring system [25]. MapReduce programming: It is a distributed parallel processing of large volume of data in a cluster with fault tolerant and reliable manner. MapReduce has job tracker and task tracker. Job tracker splits the job into tasks and schedules it to task tracker. The job tracker monitors the progress of tas k tracker. It is also respo nsible for re-executing the failed tasks. The map phase splits a user program into sub tasks and generates a set of key-value pairs. It will be submitted to reduce after a shuffle. The reduce phase performs user supplied reduce function on same key values to generate single entity. The reduce phase is also called as merge phase. The workflow of MapReduce is presented in Figure 3. The MapReduce function is represented as, map:: (input _ r e c ord) => list (key, values). reduce:: (key, list (values) => key, aggregate (values). 5.3.1. NS GA-II with MapReduce The fitness evaluation of offspring alone has done parallel in the workers available in the map phase. Non-dominated sorting, crowded tournament selection is performed on an entire population. So it cannot be fit into concurrent process. 1) Initial population is loaded into coordinator. 2) Coordinator evaluates the fitness value; perform non-dominated sorting, crowded tournament selection, crossover and mutation. The offspring generated by coordinator sends to job tracker. 3) The job tracker splits the offspring population and send to workers of map phase to evaluate fitness value in parallel manner and send it to reduce phase. 4) Shuffle opera- tion is performed between map and reduce phase. 5) The workers of reduce phase aggregate the fitness value and send it to the coordinator. Figure 3. Workflow on MapReduce and HDFS. Job TrackerName Node Map-Reduce HDFS Master User Program Task Tracker Data Node Task Tracker Data Node Task Tracker Data Node Salve 1Salve 2Salve n ….  D. Rajeswari, V. J. Senthilkumar 5.3.2. DPGA with MapReduce This approach can parallelize the distance calculation, minimum distance calculation, elite member index and fitness calculation. T he evaluation of individuals is executed par allel, because the fitness calculation is indepen- dent from others in a population. 1) The initial population is seeded into the coordinator 2) The coordinator produces the offspring population 3) The job tracker divides the offspring population into sub populations and assigns to workers in the map phase 4) The workers perform the distance calculation, minimum distance calcu- latio n, el ite me mbe r i nd ex and fit ne s s e va l uat io n for a ss i gne d ind ivi d ua ls c oncurr ent l y 5 ) The worke rs o f r ed uc e phase collect the fitness values and perform merge operation then send it back to coord inator for the next gene r- ation. 6. Simulation Results and Discussion The proposed DPGA with MapReduce model is carried out. To estimate the efficie ncy, N SGA-II with MapRe- duce model is also implemented. The metrics considered for performance evaluation are execution time, ma- kespan and flowtime. 6.1. Simulation Environment The simulation is designed by writing programs in Hadoop MapReduce using Java. Hadoop1.2.1 stable version is used to set up 4 node cluster, which is backed up by HDFS. Hadoop cluster is running on Ubuntu Linux plat- form and Java 1.6 is used for writing the code. All the 4 systems have i5 processors, 4GB RAM and 500GB hard disk. The proposed method is evaluated based on factors available in Table 1. Rand o m gener atio n wit h uni for m distribution i s used for simula tion. Resources can execute a task at a time. ETC matrix is generated depends on three metrics: task and resource heterogeneity and consistency. The various instances are labeled as x-yy-zz that represented as follows , x-consistency type (c o—consistent, ic—inconsistent, sc—semi con sistent). yy-task heterogeneity (hi—high, lo —low). zz-processor heterogene i ty (hi—high, lo—low). 6.2. Result Discussions The algorithm DPGA with MapReduce and NSGA-II with MapReduce model apply to all 12 problem instances. To compare the performance of multi-objective scheduling algorithm in a distributed computing environment, the Pareto optimal solutions p roduced by the t wo methods are plotted in Figures 4-7 for all the instances. For a better comparison of both the algorithm, each was run 10 times repeatedly with various random seeds and the best solutions are considered for b o th DPGA with MapReduce and NSGA-II with MapReduce. The makespan and mean flowtime are deliberate in same time units and obtained Pareto optimal solutions are plotted on a scale of ten thousands of time unit. The plotted graphs indicate that DPGA with MapReduce pro- duces best schedule in terms of the minimization of makespan and flowtime for all cases compared to NSGA-II MapReduce method. The algorithms are run for 1000 iterations and 100 initial populations were taken. It is also noted that the number of solutions obtained in DPGA with MapReduce increases by increasing number of Table 1 . Sp ecification setting. Specifications NSGA-II DPGA Population size 200 200 Number of iteration 1000 1000 Crossover probability (pc) 0.8 0.8 Mutation pro babili ty (pm) 0.01 0.01 Crossover type Si ngle point Single point Mutation type Swap S wa p Selection type Cr owded tournament Large tournament 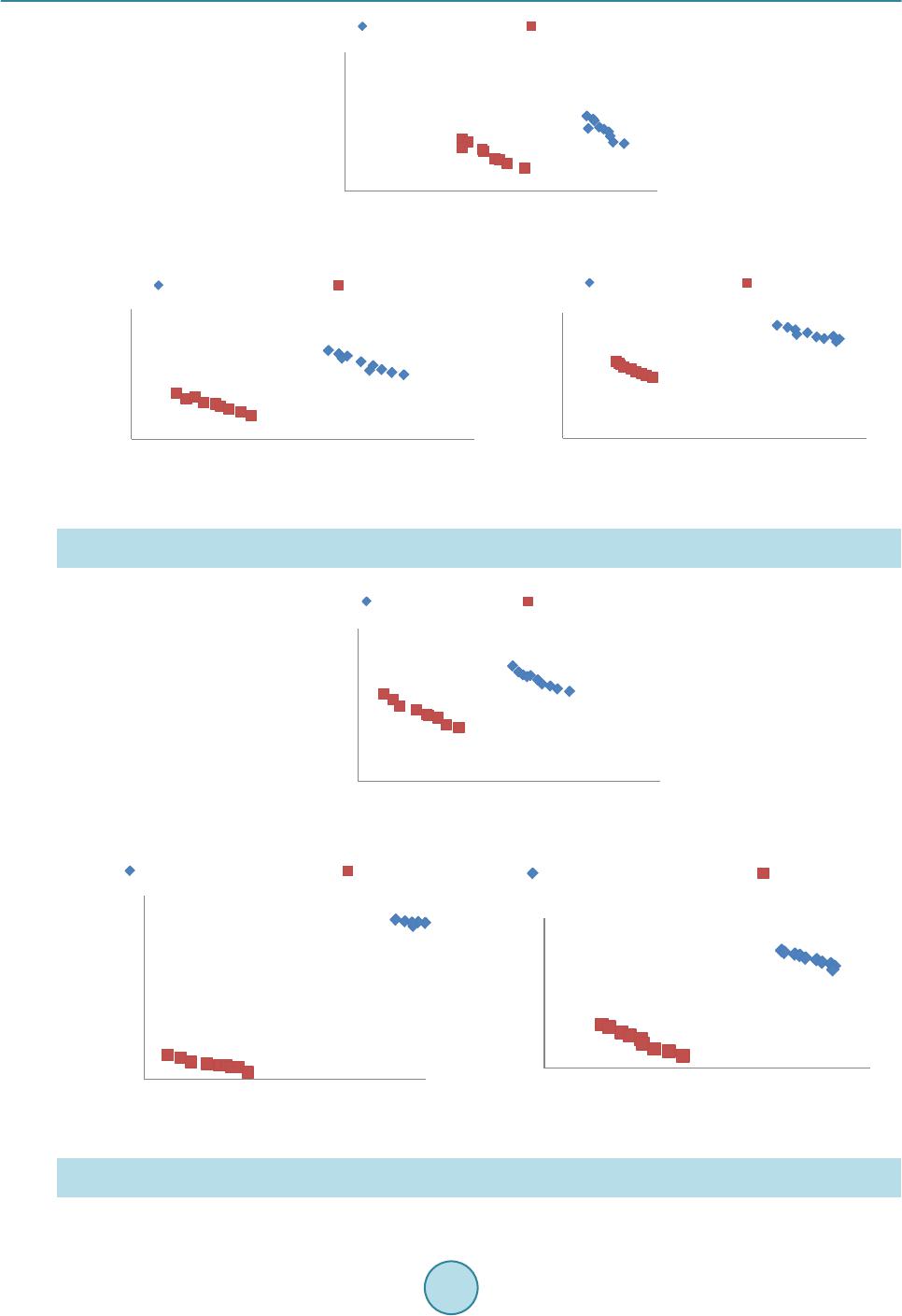 D. Rajeswari, V. J. Senthilkumar (a) (a) (b) Figure 4. NSGA-II with MapReduce and DPGA with MapReduce comparison for low task, low processor heterogeneity. (a) Consistent; (b) Semi consistent; (c) Inconsistent. (a) (b) (c) Figure 5. NSGA-II with MapReduce and DPGA with MapReduce comparison for low task, high processor heterogeneity. (a) Consistent; (b) Semi consistent; (c) Inconsistent. s_lo_hi(N SGA -II_globa l) i_lo_hi (N SGA-II_glob al)  D. Rajeswari, V. J. Senthilkumar (a) (b) (c) Figure 6. NSGA-II with MapReduce and DPGA with MapReduce comparison for high task, low processor heterogeneity. (a) Consistent; (b) Semi consistent; (c) Inconsistent. (a) (b) (c) Figure 7. NSGA-II with MapReduce and DPGA with MapReduce comparison for high task, high processor heterogeneity. (a) Consistent; (b) Semi consistent; (c) Inconsistent. 14000 14500 15000 15500 1000 1150 1300 10000 13500 17000 1100 1200 1300 1400 12000 14000 16000 18000 1100 1300 1500  D. Rajeswari, V. J. Senthilkumar population and number of iterations. Figures 4-7 show that DPGA with MapReduce model generates better makespan and mean flowtime for all consistency type, task and processor heterogeneity. 6.3. Performance Comparison of NSGA-II and DPGA The P areto optimal sol ution s et o btained b y NSG A-II, DPGA satisfy different objectives to so me extend [26]. A fuzzy based technique is used to select best compromise solution from the attained non-dominated set of solu- tions [27]. The fuzzy sets are defined using triangular membership function. Consider fma x and fmi n are maximum and minimum values of each objective function, solution in the kth objective function of a Pareto set fk is de- scribed by a membership function µk illustrated as, min max min max max min max 1, , 0, k kk kk kk kk k ff fff ff ff ff µ ≤ − = << − ≥ (12) The value of membership function indicates ho w far a non-dominated solution has satisfied the objective. In order to measure the performance of each solution to satisfy the objective, the sum of membership function val- ues µk is computed, where objectives. The performance of each non-dominated solution can be rated with respect to the entire N non-dominated solutions by normalizing its performance over the sum of the ability of N non-dominated solutions as follows, 1 11 mi k k inm i k ik µ µ µ = = = =∑ ∑∑ (13) where n is the a mount of sol ut ion a nd m is the amo unt of ob j ect ive fu nctio ns. The solu tio n has t he b est val ue of µi is the soluti on. T he ma kesp an and mean flow t ime val ue fo r the fi net ad jus tment solut ion at taine d is l isted i n Table 2. The percentage of reduction in makespan and mean flow time of DPGA with MapReduce over NSGA-II with MapReduce is calculated as, DPGA NS GA-II makespan percentage of makespan reduction1100 makespan =−× (14) DPGA NS GA-II mean flowtime percentage of mean flowtime reduction1100 mean flowtime =−× (15) The makespan and mean flow time reduction percentage is present in the Table 2. DPGA with MapReduce achieves a reduction in makespan and flowtime by 12% and 14%, over the values of NSGA-II with MapReduce. Figures 4-7 also indicates DPGA with MapReduce outperfor ms over NSGA-II with MapReduce. 6.4. Execution Time Comparison of NSGA-II and DPGA NSGA-II with MapReduce and DPGA with MapReduce is executed in single node and 4 node Hadoop cluster. The time taken by both the algorithms to find the optimal schedule is listed in Table 3. It is noted that DPGA with MapReduce has less execution time than NSGA-II with MapReduce. As the number of nodes in a Hadoop cluster is increased, the execution time of these algorithms will be reduced. 7. Conclusion In distributed computing s ystems, allo catio n of ta sks to the p ro cessing ele ment with minimu m amount o f time i s a key step for better utilization of resources. In this paper, NSGA-II with MapReduce and DPGA with MapRe- duce is implemented in DS environment and their makespan, mean flow time and execution time are compared. From the obtained results, it is noted that DPGA with MapReduce model achieves a reduction in makespan, mean flow time and execution time by 12%, 14% and 13%. The simulation results also show that the execution  D. Rajeswari, V. J. Senthilkumar Table 2 . Comparison of NSGA-II with MapReduce and DPGA wit h MapRedu ce. Instances NSGA_II with Ma pRe duce and Fuzzy DPGA with MapRe duce and Fuzzy Percentage o f Reduction in makes pan by DPGA Percentage of Reduction in mean flow time b y DPGA Makespan Mean flowtime Makespan Mean flowtime co_lo_lo 6546.28 90838. 43 5748.18 85539.56 12.19 5.83 co_lo_hi 376851.95 5133760.26 3 13263.46 4354684.62 16.87 15.18 co_hi_lo 216064.67 2846845.19 194562.67 2605329.13 9.95 8.48 co_hi_hi 12548739.42 152960763.32 10965632.48 142659273.5 12.62 6.73 sc_lo_lo 6145.27 80376.11 5259.03 70540.74 1 4.42 12.24 sc_ lo_hi 449285.18 5304352.69 388432.8 4 146759.85 13.54 21.82 sc_hi_lo 184273 .52 2368543.50 170501.59 2175234.38 7.47 8.16 sc_h i_hi 12864789.63 160436981.84 11259642.43 106847994.9 12.48 33.40 ic_lo_lo 6389.37 76943.33 5346.35 68259.43 16.32 11.29 ic_lo_hi 522843.21 5679384.21 467899.59 4938345.23 10.51 13.05 ic_hi_lo 180437.35 2344622.15 171243 .62 2132541.59 5.10 9.05 ic_hi_hi 13901746.88 167435439.5 1191359 2.13 138565274.3 14.30 17.24 Table 3. Comparison of execution time. Methods NSGA-I I with MapReduce DPGA with MapR educe Percentage of redu ction Sequential (Single node) 34.68 Sec 31.93 Sec 7.93 Parallelism w ith MapReduce (4 node Cluster) 31.714 Sec 27.64 Sec 12.85 time of these a lgorithms will be reduce d, while increasing the number of nodes in a Hadoop cluster. Future work could be extended for implementing a scheduler by using all the evolutionary kind of algorithms with the Ma- pReduce model to execute its p arallel without coordination issue. References [1] Braun, T.D., Siegel, H.J, Beck, N., Boloni, L.L., Mah es waran , M., Reuther, A.I., Robertson, J.P., Theys, M.D. and Yao, B. (2001) Comparison of Eleven Static Heuristics for Mapping a Class of Independent Tasks onto Heterogeneous Dis- tributed Computing Systems. Jour nal of Parallel and Distr ibuted Comput i n g, 61, 810-837. http://dx.doi.org/10.1006/jpdc.2000.1714 [2] Subashini, G. and Bhuvaneswari, M.C. (2011) Non Dominated Particle Swarm Optimization for Scheduling Indepen- dent Tasks on Heterogeneous Distributed Environments. International Journal of Advances in Soft Computing and Its Applications, 3, 1. [3] Kaiwartya, O., Prakash, S., Abdullah, A.H. and Hassan, A.N. (2015) Minimizing Energy Consumption in Scheduling of Dependent Tasks Using Genetic Algorithm in Computational Grid. KSII Transactions on Internet and Information Systems, 9, 8. [4] Abraham, A., Liu, H., Zhang, W. and Chang, T.G. (2006) Scheduling Jobs on Computational Grids Using Fuzzy Par- ticle Swarm Algorithm. Springer-Verlag, Berlin, Heidelberg, 500-507. http://dx.doi.org/10.1007/11893004_65 [5] Deb, K. (2002) Multi-Objective Optimization Using Evolutionary Algorithms. Wiley Publications. [6] Osycaka, A. and Kundu, S. (1995) A New Method to Solve Generalized Multicriteria Optimization Problems Using the Simple Genetic Algorithm. Structural Optimization, 10, 94-99. http://dx.doi.org/10.1007/BF01743536 [7] Wan g, F., Q iu, J., Yang, J., Dong, B., Li, X. and Li, Y. (2009 ) Hado o p Hi gh Availability through Metadata Repli cation . In: Cloud, D.B., Ed., Proceedings of the First International Workshop on Cloud Data Management. http://dx.doi.org/10.1145/1651263.1651271 [8] Munir, E.U., Li, J.-Z., Shi, S.-F. and Rasool, Q. (2007) P erformance Analysis of Task Scheduling Heuristics in Grid.  D. Rajeswari, V. J. Senthilkumar ICMLC’07: Proceedings of the International Conference on Machine Learning and Cybernetics, 6, 3093-3098. http://dx.doi.org/10.1109/icmlc.2007.4370679 [9] Mah eswaran. M. , Ali, S., Siegel, H.J., Hensgen, D. and Freund, R.F. (1999) Dynamic Mapping of a Class of Indepen- dent Tasks onto Heterogeneous Computing Systems. Jour nal of Parallel and Distributed Computing, 59, 107-131. http://dx.doi.org/10.1006/jpdc.1999.1581 [10] Freund, R.F., Gherrity, M., Ambrosius, S ., Campbell, M., Halderman, M., Hensgen, D., Keith, T., Kus s o w, M., Lima, J.D., Mirabile, F., Moore, L., Ru st , B. and Siegel, H.J. (1998) Scheduling Resources in Multiuser, Heterogeneous, Computing Environments with SmartNet. 7th IEEE Heterogeneous Computing Workshop, 184-199. [11] Abraham, A., B u yya, R. and Nath, B. (2000) Nature’s Heuristics for Scheduling Jobs on Computational Grids. The 8th IEEE International Conference on Advanced Computing and Communications (ADCOM 2000), India, 14-16. [12] Kang, Q.M. and He, H. (2011) A Novel Discrete Particle Swarm Optimization Algorithm for Meta-Task Assignment in Heterogeneous Computing Systems. Microprocessors a nd Microsystems, 35, 10-17. http://dx.doi.org/10.1016/j.micpro.2010.11.001 [13] Pacini, E., Mateos, C. and Gar i n o, C.G. (2015) Balancing Throughput and Respo nse Time in Online Scientific Clouds via Ant Colony Optimization. Adva nces in Engineering Software, 84, 31 -47. http://dx.doi.org/10.1016/j.advengsoft.2015.01.005 [14] Hossein, S., Doulabi, H., Avazbeigi, M., Arab , S. and Davoudpour, H. (2012) An Effective Hybrid Simulated Anneal- ing and Two Mixed Integer Linear Formulations for Just -in-Time Open Shop Scheduling Problem. The International Journal of Advanced Ma nu fac t ur ing Tec hno l o gy , 59, 1143-1155. [15] Izakian, H., Abraham, A. and Snasel, V. (2009) Comparison of Heuristics for Scheduling Independent Tasks on Hete- rogeneous Distributed Environments. IEEE Control Systems Magazine, 1, 8-12. [16] Abraham, A., Liu , H., Gro s an , C. and Xhafa , F. (2008) Nature Inspired Meta-Heuristics for Grid Scheduling: Single and Multi-Objective Op timization Approaches . In: X ha fa, F. and Abraham, A., Ed s., Metaheuristics for Scheduling in Dist ri buted Comp ut i ng E nv ir onme nt s , Springer Ver log, Berlin, 247-272. http://dx.doi.org/10.1007/978-3-540-69277-5_9 [17] Carretero, J., Xh a fa, F. and Abraham, A. (2007) Genetic Algorithm Based Schedulers for Grid Computing Systems. International Journal of Innovative Computing, Information and Control, 3, 1-19. [18] Lim, D., Ong, Y.-S., Jin, Y., Sendhoff, B. and Lee, B.-S. (2007) Efficient Hierarchical Parallel Genetic Algorithms Using Grid Computing. Future Generation Computing Systems, 23, 658-670. http://dx.doi.org/10.1016/j.future.2006.10.008 [19] Durillo, J.J., Nebro, A.J., Luna, F. and Alba, E. (2008) A Study of Master-Slave Approaches to Parallelize NSGA-II. IEEE International Symposium on Parallel and Distributed, Miami, 14-18 April 2008, 1-8. http://dx.doi.org/10.1109/IPDPS.2008.4536375 [20] Subhashini, G. and Bhuvaneswari, M.C. (2010) A Fast and Elitist Bi-Objective Evolutionary Algorithm for Scheduling Independent Tasks on Heterogeneous Systems. ICTACT, Journal on Soft Computing , 1, 9-17. [21] Rajeswari, D. and Jawahar Senthilkumar, V. (2015) Multiprocessor Scheduling and Performance Evaluation Using Elitist Non-Dominated Sorting Genetic Algorithm for Independent Task. International Journal on Computational Science & Applications, 5, 49-59. [22] Deb, K., Pratap, A., Agarwal, S. and Meyarivan, T. (2002) A Fast Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 6, 182-197. http://dx.doi.org/10.1109/4235.996017 [23] Rajeswari, D. and Jawahar Senthilkumar, V. (2015) Multiprocessor Scheduling and Performance Evaluation Using Distance-Based Pareto Genetic Algorithm for Independent Task. International Journal of Applied Engineering Re- search, 10, 33-38. [24] Dhole Poonam, B. and Gunjal Baisa, L. (2013) Survey Paper on Traditional Hadoop and Pipelined Map Reduce. In- ternational Journal of Computational Engineering Research, 3, 32-36. [25] http://hadoop.apache.org/docs/r1.2.1/mapred_tutorial.html [26] Niimura, T. and Nakashima, T. (2003) Multiobjective Tradeoff Analysis of Deregulated Electricity Transactions. In- ternational Journal of Electrical Power & Energy Systems, 25, 179-185. http://dx.doi.org/10.1016/S0142-0615(02)00076-5 [27] Guze k , M., Pecero, J.E., Dorronsoro, B. and Bouvry, P. (2014) Multi-Objective Evolutionary Algorithms for Ener- gy-Aware Scheduling on Distributed Computing Systems. Applie d Soft Comput ing, 24, 432-446. http://dx.doi.org/10.1016/j.asoc.2014.07.010
|