 Circuits and Systems, 2016, 7, 692-700 Published Online May 2016 in SciRes. http://www.scirp.org/journal/cs http://dx.doi.org/10.4236/cs.2016.76058 How to cite this paper: Amudha, J. and Sudhakar, R. (2016) Efficient Global Threshold Vector Outlyingness Ratio Filter for the Removal of Random Valued Impulse Noise. Circuits and Systems, 7, 692-700. http://dx.doi.org/10.4236/cs.2016.76058 Efficient Global Threshold Vector Outlyingness Ratio Filter for the Removal of Random Valued Impulse Noise J. Amudha1*, R. Sudhakar2 1Department of Electrical and Electronics Engineering, Dr. Mahalingam College of Engineering and Technology, Pollachi, India 2Department of Electronics and Communication Engineering, Dr. Mahalingam College of Engineering and Technology, Pollachi, India Received 9 March 2016; accepted 7 May 2016; published 11 May 2016 Copyright © 2016 by authors and Scientific Research Publishing Inc. This work is licensed under the Creative Commons Attribution International License (CC BY). http://creativ ecommon s.org/l icenses/by /4.0/ Abstract This research paper proposes a filter to remove Random Valued Impulse Noise (RVIN) based on Global Threshold Vector Outlyingness Ratio (GTVOR) that is applicable for real time image processing. This filter works with the algorithm that breaks the images into various decomposi- tion levels using Discrete Wavelet Transform ( DWT) and searches for the noisy pixels using the outlyingness of the pixel. This algorithm has the capability of differentiating high frequency pixels and the “noisy pixel” using the threshold as well as window adjustments. The damage and the loss of information are p reven ted by means of interior mining. This global threshold based algorithm uses different thresholds for different quadrants of DWT and thus helps in recovery of noisy image even if it is 90% affected. Experimental results exhibit that this method outperforms other exist- ing methods for accurate noise detection and removal, at the same time chain of connectivity is not lost. Keywords Image Resto ra ti on, Noise Detection, Noise Removal, Random Valued Impulse Noise, Global Threshold Vector Outlyingness Ra tio 1. Introduction Images are often corrupted by impulse noise because of sensors or channel transmission [1]. Impulse noise is *  J. Amudha, R. Sudhakar classified as fixed value impulse noise and random valued impulse noise. Generally the impulsive noise such as salt and pepper noise has the nature of producing the highest p ixel val ue (25 5) and the lowe st pixel value ( zero) in an eight bit image. This nature provid es the filtering algorithm to po int out possibilit ie s of the noise a nd has to spend only li mited co mputation p ower to ident ify exact “noise free” p ixels. The problem in real time images is that the salt and pepper noise may not occur in the form as mentioned above. Instead of pixel value 255 there may be the val ue of 25 0, which is still a sa lt noise. I nstead of pixe l value 0 t here ma y be value 1 0, which i s still a pepper noise. The existing algorithms will find difficulties in processing and removing this noise when the above mentioned change occurred in an image. In Gaussian filter [2], the Euclidean distance between the current pixel and its neighborhood is calculated. In median filter, each pixel is replaced by the median value in its neighborhood, and thus destroys the significant info rmatio n in the i mage. T o overc ome this, weighted -based median filters [3] are proposed. However, like me- dian filter, the dra wback of weigh ted-based median filters [4] is that they replace each pixel with weighted me- dian value in its neighborhood regardless of “noisy” or “noise free” pixel. The switching-based median filters have been proposed to detect “noisy” pixels replaced by median value, whereas the “noise free” pixels are left uncha nged, for exa mple, Ada ptive Switching Media n Filter (ASMF) [5]. However, these filters use median val- ues or their variations to recover the “noisy” pixels, but they introduce blur in the image details [6]. To overcome this problem, edge-preserving regularization filters are introduced by employing two-stages. In the first stage, the “noisy” pixels are identified by a noise detector. In the second stage, the “noisy” pixels are recovered by an edge preserving regularization term without affecting the edges and “noise free” pixels which have to be preserved. Papers [7]-[11] show that the noise removing capability depends on the accuracy of the noise detector in these two stage methods. To this end, this paper will employ a better noise detector for two- stage method. Local outlier-based impulse noise detectors are proposed in papers [12] recently. Local Outlier Factor (LOF) and Robust Outlyingness Ratio (ROR) are employed to identify the fixed-valued impulse noise and to measure the outlyingness of each and every pixel in the image respectively. Nor mall y ROR ha s the cap a- bility of giving the outlyingness, but it always finds the outlyingness with fixed threshold [13] [ 14 ]. A global threshold is used to find the outlyingness based on selecting better threshold for the data given. In this paper a single algorithm is proposed using Global Threshold Vector Outlyingness Ratio (GTVOR) to detect the noise as well as to remove the no ise. This technique uses the impulse-free information to r ecover the image. 2. Noise Detection and Removal 2.1. Noise Model In fixed value impulse noise, “noisy” pixels take either minimum or maximum values i.e., ηF(i, j) є {Nmin, Nmax}where Nmin = 0 and Nmax = 255, whereas Random Variable impulse noise,(RVIN) “noisy” pixels take any value within the minimum range to maximum range i.e., ηV(i, j) є [Nmin, Nmax] ,where Nmin=[0, l], and Nmax = [255 − l, 255} denote the minimum range and maximum range. Consequently, removal of variable type impulse noise is not easy compared to the removal of fixed value impulse noise. Let us consider the random valued im- pulse noise model, [ ] [ ] ( ) ( ) min , max , ,with probability ,with probability ,with probabiliy1 xy xy Np uN q o pq = −+ (1) where, p is the probab ility o f noise whose values fall i n the range of [0, l], q is the p robabili ty of noise whose values fa ll in the ra nge of [(255 − l), 255], noise probability r = p + q and p = q, ox,y and ux,y is the current pixel value of original and noisy image at coordinate (x, y). 2.2. Proposed Method Let ( ) { } ,,,1, 2,,ooxyxyM== denote M × M original image to be recovered, M is integer power of 2.  J. Amudha, R. Sudhakar RVIN is introduced during the signal acquisition stage the original image I gets corrupted. The noisy observa- tion ( )( )( ) ,, ,uxy oxynxy σ = + is obtained. To recover o(x, y) from u(x, y) is our aim, such that the Mean square Error (MSE) is less. DWT of u is matrix of wavele t c oefficie nts with 4 s ub band s ( LL, LH, HL, HH).The sub bands LH, HL and HH are detailed coefficients and LL represents approximation coefficients. We can per- form DWT of approximation sub band multiple times until the final approximation band contains only single value. De note the ma ximu m number of deco mpositions by J. T he size of the sub band at scale k is M/2k × M/2k. Figure 1 represents two level decomposition of an image. Figure 2 depicts the process carried out in removing the noise and recovering the de-noised image from the nois y ima ge. Discrete Wavelet Transform is applied for the noisy image under consideration. The decomposition level can be increased depending upon the noise level. DWT can slice the frequencies available in the image and able to give them as spatial co-ordinates for processing. The coefficient of LL, LH, HL, HH are let in to further processing. Separate the wavelet coefficients into Small Blocks with (2N + 1) × (2N + 1) window (for N = 1, 3 × 3) for the all four Coefficients i. e . LL, LH, HL, HH. Let the 3 × 3 window of wavelet coefficient be [ ] 123456789 XX ,X,X,X,X,X,X,X,X= , For this data X compute GTVOR by computing the Median(MED), Median Absolute Difference(MAD),and Global Threshold Interior Mining (GTIM) factor using the Equations (2)-(6). Global Threshold (GT) is computed using the algorithm. (2) ( ) () MADMedianbsolute XMEDA = − (3) (4) Figure 1 . Two-dimensional DWT with level-2 decomposition of an image. Figure 2 . Prop os ed me thod over vie w. 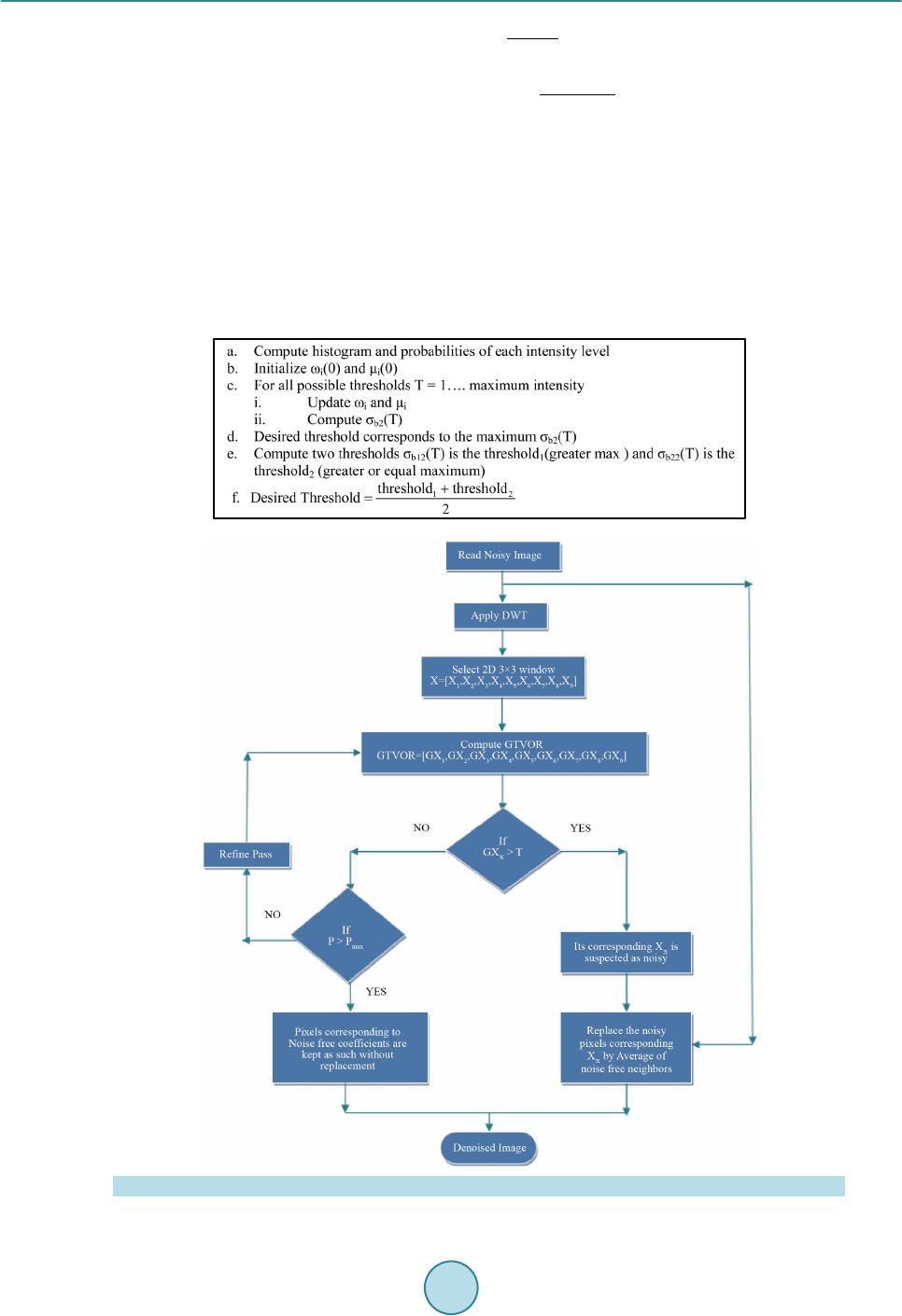 J. Amudha, R. Sudhakar (5) X MED GTVORAbsolute MADN − = (6) Let [ ] 123456789 GTVORGX,GX ,GX,GX ,GX,GX,GX ,GX,GX= . The sign of each and every ratio should be noted and floored. For example if GX3 is greate r than T h (Thr eshold), then the c orresp onding co efficie nt X3 will be suspected as noisy. The corresponding noisy pixel is rep laced by the average of th e noise free nei ghbors . This is done in spatial image. Hence we need not to use inverse transform. If the noisy pixel is not detected in this pass, the pass is incremented for further noise mining process. The iterative process of this filtering is done to r emove the noise u ntil the GT VOR detec ts no outlyingness. Thus the noise free image is recovered. Figure 3 will provide the clarity in recovering the de-nois ed i mage in steps. Algorithm to compute GT Figure 3 . Flowchart.  J. Amudha, R. Sudhakar 3. Simulation Results Standard test images of size 512 × 512 such a s Livi ng Ro om I mage , Bo at i mage, Le na I mage a nd G or illa i mage are taken from data set USC-SIPI Image Database. GTVOR algorithm is evaluated and compared with many other existing filters. For performance comparison, the Wiener filter, Median filter, Noise Adaptive Switched Median filter and Proposed GTVOR filter have been simulated by programming models and the results were tabulated in Table 1 for 80% of random valued impulse noise. The image outputs produced by various filters were compared with proposed GTVOR filter with 70% noise was presented in Figure 4. Figure 4. (a) Noise-free test images of size 512 × 512; (b) 70% noisy images; (c) Restored images by Wiener Filter; (d) Restored images by Median Filter; (e) Restored images by Adaptive Switched Median Filter; (f) Restored images by proposed GTVOR Filter.  J. Amudha, R. Sudhakar Table 1. Results in MSE, PSNR and SNR after filtering images corrupted by 80% Random valued impulse noise. Name of Im age Image Quality Parameter s 80% Noisy ima ge Wiener Filter Median Filter ASMF Proposed GTVOR Fil te r Livin g Room Image MSE 14,616.90 1997.87 9862.97 9898.38 256.58 PSNR 6.48 15.13 8.19 8.18 24.04 SNR 0.64 2.30 2.26 2.22 6.78 Boat Image MSE 14,746.87 2082.65 9937.45 9976.38 238.32 PSNR 6.44 14.94 8.16 8.14 24.36 SNR 1.42 3.69 3.02 2.99 8.04 Lena Image MSE 14,860.85 2138.40 9995.45 10,077.53 124 .69 PSNR 6.41 14.83 8.13 8.10 27.17 SNR 0.93 2.13 2.45 2.33 8.98 Gorilla Image MSE 14,423.72 1906.30 9901.85 9943.86 589.32 PSNR 6.54 15.33 8.17 8.16 20.43 SNR 0.40 2.23 1.72 1.68 4.53 Through this comparison it is clear that the proposed GTVOR filter is the best among these. The reason be- hind is the existing filters has no capability of differentiating “noisy” pixel among the group, and blindly process all the pixels. Existing filters were explor ed fully on the spatial do main of the image and implemented id entical- ly across the image, they tend to modify irrespective of noisy and noise free pixels and removes desirable details, too. Our proposed algorithm break the images into various decomposition level and searches for the anomaly/odd pixels by which the capability of noise detector is accurate than existing algorithms. Certa in algorithms such as median filter has the capability of selecting the window to process, but the capability of adjusting the high fre- quenc y noi se b y using its o wn t hresho ld val ue is not ha ndle d in t he swit ching seque nce. The se algorith ms were flexible onl y up to cer tain limit to use mean, median and mod e operations. T he ability to differe ntiate high fre- quency pixels and the “noisy pixels” using the thresholds is the best highlight of the proposed technique. The damage and the loss of information is prevented by means of interior mining capability of this algorithm. The inner mining will be more effective with bonded type noise since the proposed algorithm uses global threshold for each window in process, which makes the algorithm adaptive to any image irrespective of nature of input. The proposed GTVOR filter is tested for 512 × 512 Livin g roo m image . T he pe rfor mance of the prop ose d fil- ter is tested for all levels of noise densities. Each time the test image is corrupted by random valued impulse noise of different density ranging from 10% to 90% with an increment of 10% and tested for removal of noise capabilit y. The performance at various noise den sities for living roo m image is shown in Table 2 and plotted in Figure 5 and F igure 6. From Figure 5 and Figure 6, it is clear that Median filter and Adaptive Median filters perform better than Wie ner fi lt er whe n t he no ise l eve l i s l es s t han 40% and 50% respectively. But at high noise densities the median of wind ow its elf ha ve the effec t of nois e resu lting i n poo r qualit y in rest ori ng ima ges. As Wiener filter have the behavior of Linear time invariant that estimates the spatial intensity values of the 2D signal through which the filtering or smoothening was done. At high noise levels the estimation values will also have the effect of noise and hence restoration is poor. As the proposed filter has the capability of computing various thresholds in dif- ferent quadrants, noise detection is more accurate than all other existing filters. Comparison of histograms for 70% nois y “L iving Ro om Image” re stored by differe nt filter s is s ho wn in Figure 7. The r esul ts ar e pr o mine nt a nd t he reconstruction quality is better even at higher level of noise densities. 4. Conclusions This paper proposes a new filter, named Global Threshold Vector Outlyingness Ratio (GTVOR) Filter that  J. Amudha, R. Sudhakar Figure 5 . MSE values for different filters operating on the image “Living Room” at various noise densities. Figure 6 . PSNR values for different filters operating on the image “Living Room” at various nois e densi ties. Table 2. PSNR in dB for different filters operating on the image “Living Room” at various noise densities . Noise Density % Nois y Im a ge Weiner Filter Median Filter ASMF Proposed GTVOR Filter 10 12.54696 2 0. 45823 26.546 39 29.30889 31. 529 68 20 12.49474 2 0. 43171 26.477 96 29.15956 31. 478 64 30 10.74031 1 9. 27955 22.481 93 26.56197 29. 629 9 40 9.455607 1 8. 25742 18.418 2 23.42616 28. 279 6 50 8.524303 1 7. 45805 15.109 65 20.04897 27. 208 09 60 7.737345 1 6. 63694 12.328 69 12.318 2 6. 28682 70 7.071953 1 5. 9051 10.069 75 10.05166 25. 223 92 80 6.482251 1 5. 12513 8.1907 25 8.175163 24. 038 64 90 5.980825 1 4. 51399 6.7158 13 6.70808 21.56399 works in two stages namely detecting stage and filtering stage to recover highly-corrupted images effectively, which can be used for many real-time image processing applications. The proposed GTVOR filter is capable of suppr essing i mpulse noise e ven at high level of noise density (90%), especially, without affecting the edges and textures. Extensive experimental results depict that the proposed GTVOR filter outperforms consistently com- pared with other filters. Co mpa ring with the others existing filters, o ur filter has better ima ge r e storing cap a bility with precise noise detection. 0 2000 4000 6000 8000 10000 12000 14000 16000 18000 Adaptive Swit ched Median Filter Adaptive Switched Median Filter  J. Amudha, R. Sudhakar (a) (b ) (c) (d) (e) (f) Figure 7. Comparison of histograms for 70% noisy “living room image” restored by different filters. (a) Noise free living room image; (b) 70% noisy image; (c) Wiener filter output; (d) Median filter output; (e) Adaptive switching median filter output; (f) Proposed GTVOR filter output. According to the current research the GTVOR filter perfectly wo rk s with 8 bit images, which is used for gen- eral purp ose applic ations. T his filter has so me limitatio ns w hile worki ng with medical im ages. T he medical field has the intensive requirement for image restoration and denoising, since the medical images such as DICOM, multispectral images may involve such noise. But these images are 16 bit and the combination of pixels varies from 0 to 65535 (65536 pixel values). Therefore it is a real challenge at window decomposition of the image and in computing the outlyingness. Also the information constrained with the global threshold value varies with large interval which should be addressed in the future.  J. Amudha, R. Sudhakar References [1] Gonzalez, R.C. and Woods, R.E. (2002) Di gi tal Image Process ing. Prentice-Hall, Englewood Cliffs. [2] Wang, Z. and Zhang, D. (1999) Progressive Switching Median Filter for the Removal of Impulse Noise from Highly Corrupted Images. IEEE Transactions on Circuits and Systems—II: Analog and Digital Signal Processing, 46, 78-80. http://dx.doi.org/10.1109/82.749102 [3] Brownrigg, D.R.K. (1984) The Weighted Median Filter. Communications of the ACM, 27, 807-818. http://dx.doi.org/10.1145/358198.358222 [4] Ko, S.J. and Lee, S.J. (1991) Center weighted Median Filters and Their Applications to Image Enhancement. IEEE Transactions on Circuits and Systems, 38, 984-993. http://dx.doi.org/10.1109/31.83870 [5] Akkoul.S, Ledee, R., Leconge, R. and Harba, R. (2010) A New Adaptive Switching Median Filter. IEEE Signal Processi ng Lett er s, 17,587-590. http://dx.doi.org/10.1109/LSP.2010.2048646 [6] Nikolova, M. (2004) Avariational Approach to Remove Outl iers and Impulse Noise. Journal of Mathematical Imaging and Vision, 20, 99-120. http://dx.doi.org/10.1023/B:JMIV.0000011920.58935.9c [7] Chan, R.H., Hu, C. and Nikolova, M. (2004) An Iterative Procedure for Removing Random-Valued Impulse Noise. IEEE Signal Process ing Letters , 11, 921-924. http://dx.doi.org/10.1109/LSP.2004.838190 [8] Dong, Y., Chan, R.H. and Xu, S. (2007) A Detection Statistic for Random Valued Impulse Noise. IEEE Transactions on Ima ge Processing, 16, 1112-1120. http://dx.doi.org/10.1109/TIP.2006.891348 [9] Chan, R.H., Ho, C.W. and Nikolova, M. (2005) Salt-and-Pepper Noise Removal b y Median-Type Noise Det ectors a nd Detail Preserving Regularization. IEEE Trans ac tions on Im age Pr oce s s ing, 14, 1 479-1485. [10] Huang, Y., Ng, M.K. and Wen, Y. (2009) Fast Image Restoration Methods for Impulse and Gaussian Noise Removal. IEEE Signal Pr oc e s s ing Letters, 16, 457-460. http://dx.doi.org/10.1109/LSP.2009.2016835 [11] Allard, W.K. (2008) Total Variation Regularization for Image Denoising. SIAM Journal on Imaging Sciences, 1, 400-417. http://dx.doi.org/10.1137/070698749 [12] Wang, W. and Lu, P. (2011) An Efficient Switching Median Filter Based on Local Outlier Factor. IEEE Signal Processi ng Lett er s, 18, 551-554. http://dx.doi.org/10.1109/LSP.2011.2162583 [13] X iong, B. and Yin, Z. (2012 ) A Universal Den oising Framework with A New Impulse Detector and Nonlocal M eans. IEEE Tra ns ac t i ons on Image P r o c e s s i ng, 21, 1663-1675. http://dx.doi.org/10.1109/TIP.2011.2172804 [14] Breuig, M.M. (2000) LOF: Identifying Density-Based Local Outliers. Proceedings of the ACM SIGMOD Conference on Management of Data, Dallas, 15-18 May 2000, 93-104. http://dx.doi.org/10.1145/335191.335388
|