Received 13 March 2016; accepted 6 April 2016; published 13 April 2016

ABSTRACT

The standard Ginzburg-Landau (GL) equations are only valid in the vicinity of the critical temperature. Based on the Eilenberger equations for a single band and s-wave superconductor, we derive a modified version of the standard GL equations to improve the applicability of the standard formalism at temperature away from the critical temperature. It is shown that in comparison with previous studies, our method is more convenient to calculate and our modified equations are also compatible with a dirty superconductor. To illustrate the usefulness of our formalism, we solve the modified equations numerically and give the magnetic field distribution in the mixed state at any temperature. The results show that the vortex lattice could be still observed even away from the critical temperature (e.g., T/T_c = 0.3).

Keywords:

Modified GL Equations, Vortex Lattice

1. Introduction

As is well known, the Ginzburg-Landau (GL) theory is an effective phenomenological theory to describe superconductivity [1]. The main concept is that the free energy functional of superconductors can be expressed by the power series of order parameters in the vicinity of the critical temperature. Minimization of the functional gives the GL equations that can describe the spatial field distribution in superconductors. By solving the linearized GL equations, Abrikosov predicted the flux lattice and proposed the criterion of type II superconductors [2]. However, strictly speaking, the GL equations are only valid in the vicinity of the critical temperature [3].

Since the classical work by Gorkov [3] [4], GL equations can be derived from the BSC theory via the Green functions. Then, based on the Gorkov equations, Eilenberger proposed a kind of simplified formalism via the quasi-classical Green functions [5]. A transformation of the Eilenberger equations from partial differential equations into ordinary differential equations enables the numerical study of the field distribution in the mixed state [6] [7]. But all of these works are based on the microscopic theory, which is not convenient enough compared with the GL theory.

Vagov et al. extended the GL equations from the Gorkov theory [8]-[10], so that they can be applicable to any finite temperature cases. However, to establish their formalism needs to calculate multiple integrals, and their formalism is only valid for a clean superconductor. In this paper, we develop a more convenient approach to derive a set of modified GL equations from the Eilenberger equations, which are applicable to any finite temperature cases. Our formalism is not only valid for a clean superconductor, but also for a dirty one. Then, to illustrate the validity of our formalism, we will solve the modified equations numerically and investigate the temperature dependence of the field distribution in the mixed state. Here, we discuss the single band, s-wave superconductor, and we adopt the ansatz that the Fermi surface is a sphere.

2. Theoretical Analysis

Eilenberger defines the quasi-classical Green function and the quasi-classical abnormal Green function 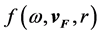[5], where is the Matsubara frequency, and 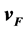denotes the vector of Fermi velocity on the Fermi surface. Considering the isotropic impurity scattering, one can define the relaxation time for scattering. The gauge-invariant gradient is, and its conjugate is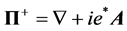, where A is the vector potential. The Eilenberger equations take the form

(1a)

(1b)

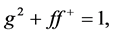(1c)

where the angular bracket denotes an average over all on the Fermi surface. For a single band, s-wave superconductor, the self-consistent equations about gap function and current density are given by

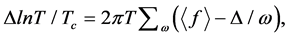(2)

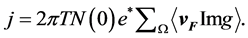(3)

Here is the density of state. Actually the gap function 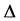is the order parameter in the GL theory.

In the absence of magnetic fields, for a clean superconductor (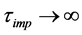), Equations (1) can be transformed into algebraicones, which yield and. and can be regarded as zero order terms, while the applied magnetic field and the impurity scattering are regarded as the perturbation [11]. Accordingly, the quasi-classical Green functions are expressed as

and,

where the subscripts 1, 2 indicate the first-order and second-order correction terms respectively. Substituting these forms into Equations (1), one will obtain a set of recursive relations. However, the behavior of this expansion is similar o an asymptotic expansion in mathematics, which is valid only for the case that the anisotropy of g and f is weak in a weak magnetic field or in a dirty sample with strong impurity scattering, and otherwise it will be divergency. Therefore, to avoid such difficulties, we regard the Green functions in the vicinity of the

critical temperature as the zero order terms. By introducing and, the Eilenberger equations can be rewritten as

(4a)

(4b)

In this form, for a clean superconductor at zero magnetic field, the zero order terms are and. Owing to, the factor can be expressed as the convergent power series expansion of. Therefore, the quasi-classical Green functions f and g can be denoted by the convergent power series expansion of and. In addition, considering the contribution of the

magnetic field and impurity scattering, one can deal with Equations (4) by the perturbation procedure. On the account of several perturbation parameters in these expressions, we can choose the parameter to control relevant quantities so that we can adopt a single-small-parameter series expansions for Equations (4). In our consideration, and have the same order, and the impurity scattering is regarded as a parameter independent of the former quantities.

Thus, all correction terms for the quasi-classical Green functions can be obtained by the perturbation procedure. Then, substituting the function f in the gap equation; collecting all the terms of and calculating the summation, one can prove that. Next, express the term as the power series of. After some algebraic calculation, collecting all the terms with the order lower than, we will obtain a new equation

(5)

Because of the spherical Fermi surface, the odd number of power about the operator will vanish after the average over the Fermi surface. Similarly, the expansion of g is substituted in Equation (3), and the even number of power about the operator will vanish. Finally, we will obtain the current density,

(6)

Oh represents the higher order correction. By introducing and defining the function, the coefficients of each term are given by,

, ,

, ,

, , ,

,

,

, (7)

These are valid for arbitrary impurity concentration. represents the higher order correction in each coefficient. The general form is too complicated to give analytical coefficients. However, if our concern is focused on a clean limit case, indicating, the function can be expressed by Riemann zeta function, i.e., , where denotes the Riemann zeta function. On the other hand, if the impurity scattering is strong enough that, the function can also be expressed by.

Since Equation (5) and Equation (6) always contains the higher order corrections, they cannot be solved directly. By considering the perturbation procedure again, is written as and j as. Equation (5) and Equation (6) can be separated by collecting all the terms according to the order of, and finally a set of recursion relation will be derived, so that the inconvenience caused by the higher order corrections will be eliminated. Besides, since the operator contains the vector potential A, which

subjects to the relation, the operator should also be written as (where,). As a result, by collecting all the terms of the order, we will obtain

(8a)

(8b)

Here, the numbers in the superscript bracket stand for the order inside the coefficient. Near the critical temperature, the higher order terms can be neglected, and only the functions and should be con-

sidered. In fact, Equations (8) are the standard GL equations. But if the temperature is much lower than the critical temperature, the effect caused by becomes so obvious that the higher order terms about must be retained. Hence the functions and need to be calculated. By collecting all the terms of the order, the equations read as,

(9a)

(9b)

Obviously, these equations have much more complicated form than Equations (8). The contribution caused by temperature and magnetic field reveals the nonlinear relation, which cannot be derived from the standard GL equations. That is to say, the Equations (9) is a set of modified relation for Equations (8). As the GL equations have been modified, the free energy functional should also be modified as,

(10)

Following previous recursive procedure, the free energy can be calculated in the same way as well. In addition, the standard GL equations give linear relations between characteristic lengths (penetration length and coherent length) and temperatures. However, if the higher order terms are considered, the linear relations need to be modified to nonlinear relations as well.

The same result has been reported in a series of Vagov’s papers, which is derived from the Gorkov equations [8]-[10]. However, to establish their formalism needs to calculate complex multiple integrals. And it is difficult to discuss the convergence property of each term. As a result, they only present the case for a clean superconductor. In our derivation, the quasi-classical version avoids the calculation of the multiple integral. We only need to consider the iteration of the quasi-classical Green function, so that the convergence property of each term in our formalism is clear. Besides, form above discussion, it is obvious that our modified equations are not only application to a clean superconductor but also to a dirty superconductor. And the only differences between them are the coefficients.

Next, we will investigate the magnetic field in a bulk superconductor to illustrate the validity of our formalism.

3. Numerical Simulation

Abrikosov had studied the vortex lattice by solving the standard GL equations near the upper critical field. According to his work, more general solutions of the GL equations were elaborated by Z. Hao et al. [12] and Brandt [13] [14] by means of different numerical methods. However, their works are based on the standard GL equations, so their theoretical results are valid near the critical temperature. Now, we discuss the magnetic field distribution at any temperature by means of our modified GL equations.

Because of the spatial periodicity of vortex lattice, the order parameter and the vector potential can be analyzed with the help of the Fourier series. In practical computation, the order parameter is a complex-value function, which does not perform the spatial periodicity, so it cannot be expressed as the Fourier series directly.

Introduce the square of the magnitude of the order parameter, , which is a real-value and periodic function, where, so that u can be expressed by the Fourier series expansion. As for the phase of the order parameter, it is hardly to write an explicit expression. Since the working factor is the phase gradient instead of the phase itself, we can introduce the super velocity to express it. Obviously, the induced magnetic field can also be denoted by the Fourier series expansion.

Here, we consider a large enough bulk superconductor and set the direction of the magnetic field along the z axis. In this way, the order parameter and the magnetic field are only determined by variable x and y, so that our problem is simplified to a 2 dimensional (2D) case. Since every flux line carries the flux quantum with integer number, the flux lines are periodically embedded in unit cells one by one. In 2D space, the period of the vortex

lattices is described by the vector (m, n integer), where, , , and a or b is the length of the sides of a parallelogram unit cell; θ is the angle between a and b. Correspondingly the reciprocal lattice vector is. The size of the unit cell will be determined by the relation, where is a flux quantum; is the average induced field; S is the area of a unit cell and is the number of flux quantum. Here, we consider the hexagonal structure () [15], so u and B are respectively expressed as

(11)

(12)

with r = (x, y). The Fourier coefficients and are complex numbers. Since u and B are real-valued functions, there are conjugate relations between different coefficients, ,. Besides, we

only define the expression of B, but not define specific expression of q, because q can be expressed by the Maxwell equations. Our task is to determine the coefficients of the ansatzs (11) and (12) to make the modified equations true. In order to find the proper coefficients, we can employ a fast Fourier transformation method introduced by Ref. [13]. The iteration procedure for the Fourier coefficients can be achieved by the modified GL equations. According to this method, each equation can be expressed as the form,

(13a)

(13b)

Obviously, the Laplacian on the left side of equations yields the factor. The remaining terms are

put to the right side as a kind of “inhomogeneity”, whose coefficients are determined by the last iteration. Using the orthogonality of the Fourier series expansion, one can obtain a set of new coefficients. Then, we substitute new coefficients into the right side, and repeat this step constantly, until obtain the optimal solution. Here the parameters α and β are chosen artificially to control the iteration procedure convergence. Therefore, coefficients are given by,

(14)

(15)

Here the angular bracket denotes the integral over a unit cell. This method is computed much faster than direct optimization methods. After a few steps of iterating, they will yield the coefficients. Thus, the vortex lattice at any temperature will be determined.

We have mentioned above that the modified GL equations for a clean superconductor and a dirty superconductor only have the different coefficients, so the equations will yield the similar results for both cases. Here, we

only discuss the case for a clean superconductor with to elaborate on the temperature effect on the magnetic field distribution. The GL parameter of clean superconductor is, which does not depend on temperature.

Since the filed distribution is determined by the average induced field, we can recall the relation to determine the applied field, where F is the free energy functional. In terms of the virial theorem, it can be simplified as [16]

(16)

In our modified free energy functional (10), is given by

Keeping the magnetic field unchanged, we change the temperature to investigate the magnetic field distribution. Here, introduce to make the magnetic field dimensionless, i.e., using in the next. The average induced field is set to, and the temperature is respect-

tively. The results are shown in Figure 1. The different colors stand for different magnitudes of the magnetic field, and the applied filed is labeled on each figure. This result is more reliable than the result derived from the standard GL equations. From Figure 1, on the condition of, the magnetic field is near the upper critical field, and the interaction of flux lines is extremely strong. The fluctuation of induced field is so small that the field can be regarded as homogeneous field. As for or，the fluctuation of induced field is not small, and the independent flux lines can be observed more easily.

Further, we take into account the magnetic field dependence of the vortex lattice away from the critical temperature. Here, we choose the condition of (). When the cases of and are computed respectively, the numerical simulation yields negative value of correction terms for, while yields positive value for. This phenomenon is interesting. According to the standard GL equations, the upper critical field at is given by. It seems to be no problem. But if we recall the WH theory for a clean superconductor [17], the upper critical field at is given by. The reason is explicit. On the condition of, the vortex lattice will be unstable or inexistence because the magnetic field is higher than the upper critical field. That is to say we cannot obtain the correct solution on the condition of. Therefore, according to the modified equation, we can also determine the vortex more accurately. To assure the stable vortex lattice, the average induced field should be lower than the upper critical field. Here, we choose the case of to compute respectively, and the results are in Figure 2. In this figure, for the case of, the scale of adjacent vortex is about 0.15 unit length, while the scale extends to 0.78 unit length for the case of. Hence, we conclude that the filed effect on the scale of unit cells is much more prominent than the deformation of vortex.

From Figure 1 and Figure 2, we numerically prove that the vortex lattice will exist away from the critical temperature, which cannot be derived from the standard GL equations. So we can conclude that the modified equations improve the applicability of the standard formalism.

4. Conclusion

In this paper, we derived the modified version of the standard GL equations for an s-wave superconductor from the Eilenberger equations. Comparing with other studies, our derivation assures that each term in expansion will not be divergency when finite terms are taken into account, and greatly simplifies the complex calculations. In addition, our modified equations are valid for both a clean and a dirty superconductor at any temperature. With the help of the Fourier series, the modified equations were solved numerically, which could help us analyze the magnetic field distribution away from the critical temperature. Based on this, we theoretically proved the existence of the vortex lattice at low temperature. As a result, we confirmed that the modified equations improve the applicability of the standard formalism.

Acknowledgements

The authors acknowledge the financial support from the National Natural Science Foundation of China (NSFC) (Grant NO.11274401).

Cite this paper

Ruiqi Huang,Weilong She, (2016) The Magnetic Field Distribution of Type II Superconductors Based on the Modified GL Equations. Journal of Applied Mathematics and Physics,04,669-676. doi: 10.4236/jamp.2016.44077

References