Received 14 March 2016; accepted 6 April 2016; published 13 April 2016

ABSTRACT

In this paper, estimations of the lower solution bounds for the discrete algebraic Lyapunov Equation (the DALE) are addressed. By utilizing linear algebraic techniques, several new lower solution bounds of the DALE are presented. We also propose numerical algorithms to develop sharper solution bounds. The obtained bounds can give a supplement to those appeared in the literature.

Keywords:

Discrete Lyapunov Equation, Estimation, Lower Solution Bound, Linear Algebraic Technique

1. Introduction

It is known that the Lyapunov equation is widely used in various control systems. Furthermore, solution bounds of the above equation can also treat many control problems. For example, robust stability analysis for time-delay systems, robust root clustering for linear systems, determination of the size of the estimation error for multiplicative systems, and others can be solved by the mentioned solution bounds. Gajic and Qureshi [1] explained one motive for studying the solution bounds of the Lyapunov equation: sometimes we are simply interested in the general behavior of the underlying system, and this behavior can be determined by examining certain bounds on the parameters of the solution, rather than the full solution. During the past few decades, research on deriving solution bounds of the Lyapunov equation has become an attractive research topic, and a number of research approaches have been proposed to this problem [2]-[9]. Among those results, they focus on the evaluation for the bounds of single eigenvalues including the extreme ones, the trace, the determinant, as well as the bounds of solution matrix. In fact, it has been observed that all the aforementioned solution bounds can be defined by matrix bounds. Hence, the matrix bounds are the most general findings. In the literature, matrix bounds of the solution of the DALE have been studied in [3] [5]-[8]. Many good bounds have been presented. However, it seems that most of these approaches for the matrix bounds contain points of weakness. For example, those results proposed in [5]-[7] must assume that the matrix Q is positive definite. In many control problems, this matrix may be positive semi-definite. Bounds in [5]-[7] also have inverse matrices and the computation burden hence may become very heavy when the system dimension becomes large. The matrix A must be normal in one of the bound presented in [7] and must be diagonalizable in [6]. For another bound in [7], an extra Lyapunov equation must be solved. Furthermore, in [5], the lower solution bound has a free matrix and how to choose this matrix such that the obtained bound is the best is still an open problem. To give a supplement to those appeared in the literature is therefore the aim of this paper. A new approach for developing lower matrix bounds of the solution of the DALE then is proposed. In what follows, it is not necessary to assume that Q is positive definite and A is diagonalizable or normal. Several matrix bounds for the DALE (1) are developed by a simple approach. In addition, the presented results do not involve any free variable. Therefore, in comparison with existing literature on the subject, the proposed results are less restrictive and more easily calculated.

2. Main Results

Consider the discrete algebraic Lyapunov Equation (DALE) which are represented by

(1)

where, A is a stable matrix, Q denotes a given positive semi-definite matrix, and P is the unique positive semi-definite solution.

Before developing the main results, we review the following useful result.

Lemma 1 [10]: Let a real symmetric matrix U be defined as

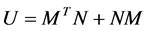(2)

where is a given positive semi-definite matrix. Then if and only if the 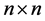real matrix is negative semi-definite then U is negative semi-definite.

Then, by utilizing lemma 1 and some linear algebraic techniques, new lower matrix bounds of the solution of the DALE (1) are derived as follows.

Theorem 1. The solution P of the DALE (1) has the following bounds.

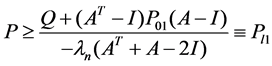(3)

and

(4)

where the positive semi-definite matrices and 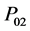are defined, respectively, by

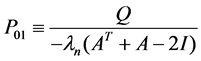(5)

and

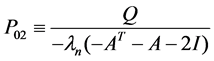(6)

Proof. Let a positive semi-definite matrix R is defined as

. (7)

Then we have

(8)

which infers

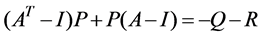. (9)

It is seen that by using the positive semi-definite matrix R, the DALE (1) can be transformed into a continuous-type Lyapunov Equation (9). Then, by (9), we rewrite the DALE (1) as

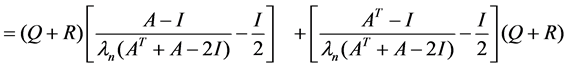(10)

Since A is stable, we have and.Then

(11)

and

(12)

Then, according to Lemma 1, it is seen that the right-hand side of Equation (10) is negative semi-definite. Therefore, Equation (10) is a continuous Lyapunov equation and its solution is positive semi-definite. That is,

(13)

Define

(14)

The DALE (1) now can be rewritten as

(15)

Then, we have

(16)

Due to the facts that

(17)

and

(18)

the right-hand side of (16) then is negative semi-definite. Therefore, the solution of the Lyapunov Equation (16) is positive semi-definite. We have

(19)

Substituting and into (13) and (19), respectively, and from the definitions R and gives

(20)

and

(21)

Thus, the proof is completed.

Remark 1. According to the proof of Theorem 1, it is seen that if and are substituted into (19) and (13), respectively, we can also obtain the following results without proof.

Corollary 1. The solution P of the DALE (1) satisfies

(22)

and

(23)

where matrices and are defined by (5) and (6), respectively.

Remark 2.It is found that if then. This leads to and. Besides, it is seen that for. For this case, we have and. The tightness between bounds and, respectively, cannot be compared. Maybe they can give a supplement to each other. However, from Theorem 1, the following algorithms can be developed for obtaining tighter lower solution bound for the DALE (1).

Algorithm 1.

Step 1. Set.

Step 2. Compute

(24)

Then, comparing to, are tighter solution bounds for the DALE (1).

Proof. Let. From Step 1 and (24), we have

(25)

Now, we assume

.

Then the definition of yields

(26)

By the inductive method, one can conclude that.

Algorithm 2.

Step 1. Set.

Step 2. Compute

(27)

Then, solution bounds of the DALE (1) are tighter than.

Proof. Let. From Step 1 and (27), we have

. (28)

Now, we assume

.

Then the definition of yields

. (29)

By the inductive method, one can conclude that.

Remark 3. Surveying the literature, existing lower matrix bounds of the solution of the DALE (1) are summarized as follows.

[5] (30)

[3] (31)

, [7] (32)

, with [7] (33)

[8] (34)

[6] (35)

where

with (36)

(37)

where (38)

, with (39)

(40)

(41)

where (42)

the degree of the minimal polynomial of A. (43)

From the above conditions, it is seen that most of them contain points of weakness. The matrix Q in [5]-[7] must be positive definite. In many control problems, this matrix may be positive semi-definite. It is also seen that bounds in (30), (33), and (35) have inverse matrices. The computation burden hence may become very heavy. The matrix A must be normal in (33) and must be diagonalizable in (35). For bound (32), an extra Lyapunov equation must be solved. Furthermore, from (39), it is obvious that the computation of constants is very difficult. From the obtained results of this work, it is not necessary to assume that the matrix A is diagonalizable or normal. We also do not assume that the matrix Q is positive definite. Furthermore, the present bounds do not involve any inverse matrix and hence are easy to be evaluated. It is found the tightness of the obtained results and those appeared in the literature cannot be compared by any mathematical method. However, at least they can give a supplement to each other.

3. A Numerical Example

Example 1. Consider the DALE (1). Matrices A and Q are chosen as

and

where matrix A is diagonalizable and normal and Q is positive definite. In this case, we choose

.

Then, from the obtained results and (30)-(35), solution bounds of the DALE (1) for this case are shown below.

For this case, it is seen that, , and. However, the sharpness between, , and cannot be compared. It shows that the obtained results and those appeared in the literature can give a supplement to each other. By using Algorithm 1, we have

for.

Obviously our result now is tighter than the parallel ones in this case. This means that the presented algorithms indeed can work.

4. Conclusion

In this paper, the lower matrix bounds of the solution for the DALE have been discussed. By transform the DALE into a continuous-type Lyapunov equation, we have established several concise lower solution bounds of the DALE. All proposed bounds are new and less restrictive than the majority of those appeared in the literature. According to some of these results, iterative algorithms have also been developed for obtaining sharper lower matrix bounds. Finally, we give a numerical example to demonstrate the applicability of the presented schemes.

Acknowledgements

The author would like to thank the National Science Council for financial support of this research under the grant MOST 104-2221-E-230-009.

Cite this paper

Chien-Hua Lee, (2016) On the Measurement of Lower Solution Bounds of the Discrete Algebraic Lyapunov Equation. Journal of Applied Mathematics and Physics,04,655-661. doi: 10.4236/jamp.2016.44075

References