Journal of Applied Mathematics and Physics
Vol.04 No.04(2016), Article ID:65457,7 pages
10.4236/jamp.2016.44074
Nonlinear Super Integrable Couplings of a Super Integrable Hierarchy
Sixing Tao
School of Mathematics and Information Science, Shangqiu Normal University, Shangqiu, China



Received 1 March 2016; accepted 6 April 2016; published 13 April 2016
ABSTRACT
Nonlinear super integrable couplings of a super integrable hierarchy based upon an enlarged matrix Lie super algebra were constructed. And its super Hamiltonian structures were established by using super trace identity. As its reduction, special cases of this nonlinear super integrable coupling were obtained.
Keywords:
Lie Super Algebra, Nonlinear Super Integrable Couplings, A Super Integrable Hierarchy, Super Hamiltonian Structures

1. Introduction
With the development of soliton theory, super integrable systems associated with Lie super algebra have aroused growing attentions by many mathematicians and physicists. It was known that super integrable systems contained the odd variables, which would provide more prolific fields for mathematical researchers and physical ones. Several super integrable systems including super AKNS hierarchy, super KdV hierarchy, super KP hierarchy, etc., have been studied in [1]-[4]. There are some interesting results on the super integrable systems, such as Darboux transformation in [5], super Hamiltonian structures in [6] [7], binary nonlinearization [8] and reciprocal transformation [9] and so on.
The research of integrable couplings of the well known integrable hierarchy has received considerable attention [10]-[12]. A few approaches to construct linear integrable couplings of the classical soliton equation are presented by permutation, enlarging spectral problem, using matrix Lie algebra [13] constructing new loop Lie algebra and creating semi-direct sums of Lie algebra. Recently, You [14] presented a scheme for constructing the nonlinear super integrable couplings for the super integrable hierarchy. Zhang [15] once constructed an integrable hierarchy and discussed Lax representation, Darboux transformation for its constrained flows. Shi [16] constructed the super extension of this hierarchy.
In this paper, we hope to construct nonlinear super integrable couplings of this super integrable hierarchy which was constructed in [16] through enlarging matrix Lie super algebra. We take the Lie algebra  as an example to illustrate the approach for extending Lie super algebras. Based on the enlarged Lie super algebra
as an example to illustrate the approach for extending Lie super algebras. Based on the enlarged Lie super algebra , we work out nonlinear super integrable Hamiltonian couplings of this super integrable hierarchy. Finally, we will reduce the nonlinear super integrable couplings to some special cases.
, we work out nonlinear super integrable Hamiltonian couplings of this super integrable hierarchy. Finally, we will reduce the nonlinear super integrable couplings to some special cases.
2. Enlargement of Lie Super Algebra B(0, 1)
Consider the Lie super algebra B(0, 1). Its basis is
 (1)
(1)
where  are even element and
are even element and 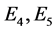 are odd elements. Their non-zero (anti) commutation relations are
are odd elements. Their non-zero (anti) commutation relations are
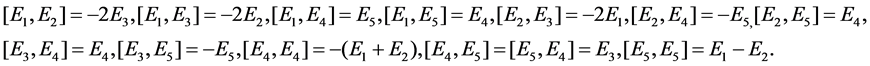 (2)
(2)
Let us enlarge the Lie super algebra B(0, 1) to the Lie super algebra gl(6, 2) with a basis
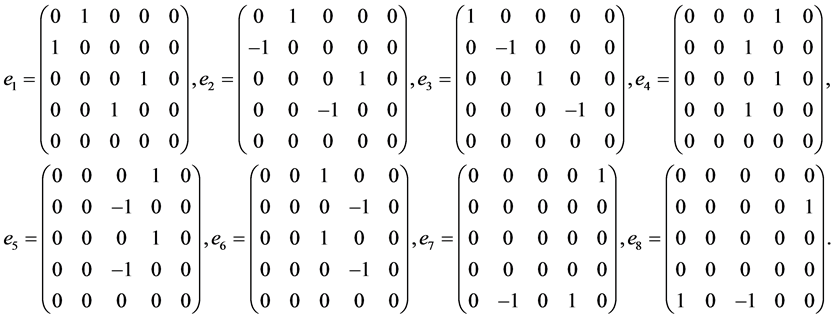 (3)
(3)
where 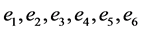 are even, and
are even, and  are odd.
are odd.
The generator of Lie super algebra gl(6, 2), 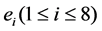 satisfy the following (anti) commutation relations:
satisfy the following (anti) commutation relations:

(4)
Define a loop super algebra corresponding to the Lie super algebra gl(6, 2), denote by
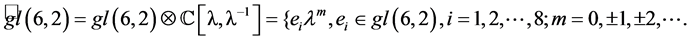 (5)
(5)
The corresponding (anti)commutative relations are given as
 (6)
(6)
3. Nonlinear Super Integrable Couplings of a Super Integrable Hierarchy
If Let us start from an enlarged spectral problem associated with gl(6, 2),
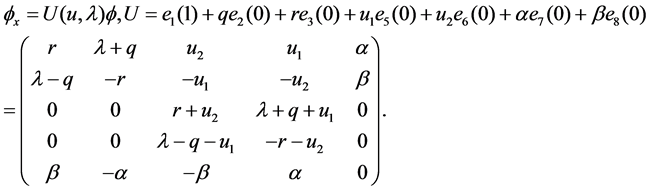 (7)
(7)
where 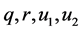 are even potentials, but
are even potentials, but  are odd ones.
are odd ones.
In order to obtain super integrable couplings of super integrable hierarchy, we solve the adjoint representation of (7),
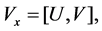 (8)
(8)
with
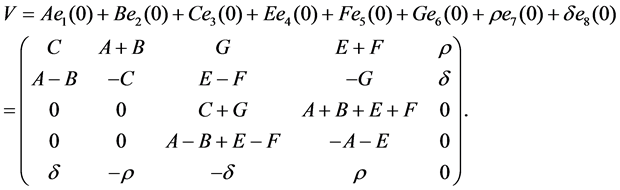
where 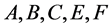
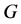
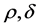
Substituting

into previous equation gives the following recursive formulas
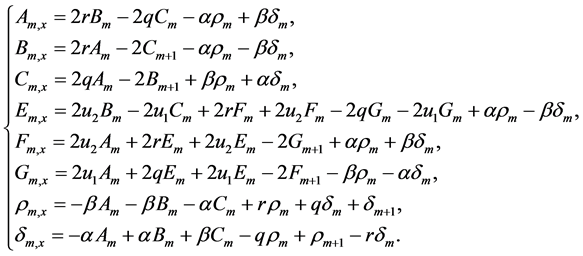
From previous equations, we can successively deduce
Equations (11) can be written as

where
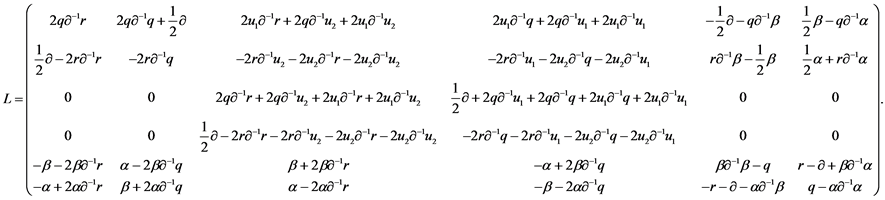
Then, let us consider the spectral problem (7) with the following auxiliary problem
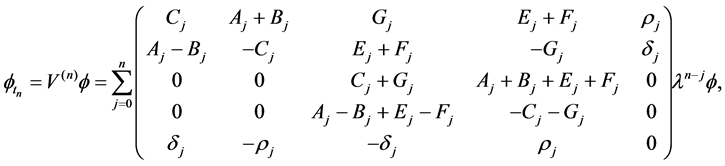
From the compatible condition 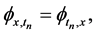
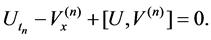
which gives a nonlinear Lax super integrable hierarchy
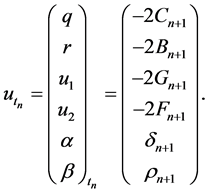
The super integrable hierarchy (16) is a nonlinear super integrable couplings for the integrable hierarchy in [16]
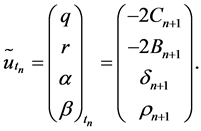
4. Super Hamiltonian Structure
A direct calculation reads
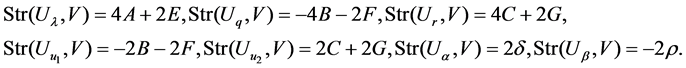
Substituting above results into the super trace identity [7]
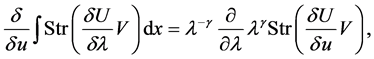
and comparing the coefficients of 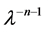
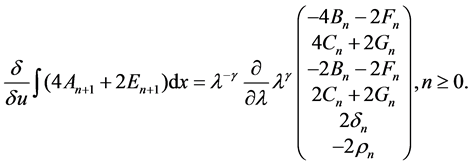
From the initial values in (11), we obtain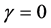
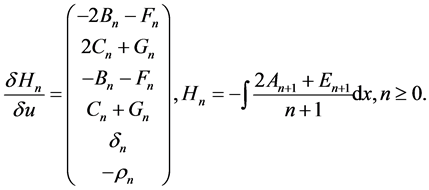
It then follows that the nonlinear super integrable couplings (16) possess the following super Hamiltonian form
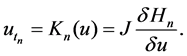
where
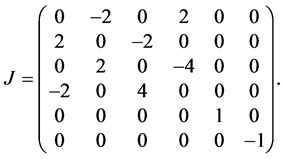
is a super Hamiltonian operator and 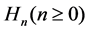
5. Reductions
Taking 
When 
Let 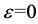
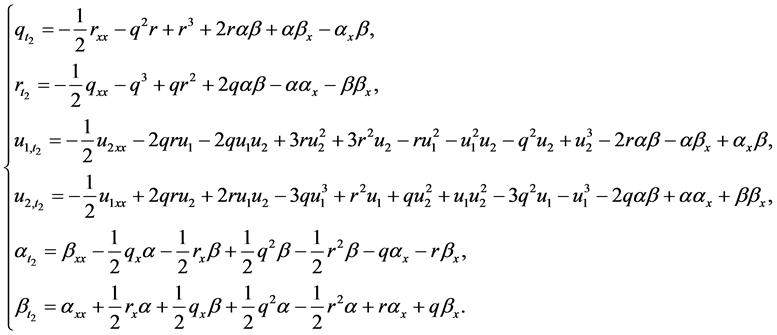
Especially, taking 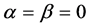
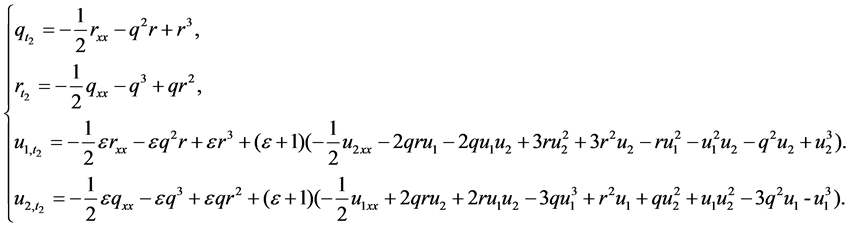
If setting 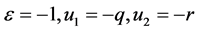

6. Conclusion
In this paper, we introduced an approach for constructing nonlinear integrable couplings of super integrable hierarchy. Zhang [17] once employed two kinds of explicit Lie algebra 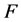
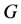

in [17] is isomorphic to the Lie algebra span 
able couplings of super GJ and Yang hierarchy easily. The method in this paper can be applied to other super integrable systems for constructing their super integrable couplings.
Acknowledgements
This work was supported by the Natural Science Foundation of Henan Province (No.132300410202), the Science and Technology Key Research Foundation of the Education Department of Henan Province (No. 14A110010), the Youth Backbone Teacher Foundation of Shangqiu Normal University(No. 2013GGJS02).
Cite this paper
Sixing Tao, (2016) Nonlinear Super Integrable Couplings of a Super Integrable Hierarchy. Journal of Applied Mathematics and Physics,04,648-654. doi: 10.4236/jamp.2016.44074
References
- 1. Kupershmidt, B.A. (1985) Odd and Even Poisson Brackets in Dynamical Systems. Letters in Mathematical Physics, 9, 323-330. http://dx.doi.org/10.1007/BF00397758
- 2. Li, Y.S. and Zhang, L.N. (1988) A Note on the Super AKNS Equations. Journal of Physics A: Mathematical and General, 21, 1549-1552. http://dx.doi.org/10.1088/0305-4470/21/7/017
- 3. Tu, M.H. and Shaw, J.C. (1999) Hamiltonian Structures of Generalized Manin-Radul Super-KdV and Constrained Super KP Hierarchies. Journal of Mathematical Physics, 40, 3021-3034. http://dx.doi.org/10.1063/1.532741
- 4. Liu, Q.P. and Hu, X.B. (2005) Bilinearization of N = 1 Supersymmetric Korteweg de Vries Equation Revisited. Journal of Physics A: Mathematical and General, 38, 6371-6378. http://dx.doi.org/10.1088/0305-4470/38/28/009
- 5. Aratyn, H., Nissimov, E. and Pacheva, S. (1999) Supersymmetric Kadomtsev-Petviashvili Hierarchy: “Ghost” Symmetry Structure, Reductions, and Darboux-Ba ?cklund Solutions. Journal of Mathematical Physics, 40, 2922-2932. http://dx.doi.org/10.1063/1.532736�
- 6. Morosi, C. and Pizzocchero, L. (1993) On the Bi-Hamiltonian Structure of the Supersymmetric KdV Hierarchies. A Lie Superalgebraic Approach. Communications in Mathematical Physics, 158, 267-288. http://dx.doi.org/10.1007/BF02108075
- 7. Hu, X.B. (1997) An Approach to Generate Superextensions of Integrable Systems. Journal of Physics A: Mathematical and General, 30, 619-632. http://dx.doi.org/10.1088/0305-4470/30/2/023
- 8. He, J.S., Yu, J., Zhou, R.G. and Cheng, Y. (2008) Binary Nonlinearization of the Super AKNS System. Modern Physics Letters B, 22, 275-288. http://dx.doi.org/10.1142/S0217984908014778
- 9. Liu, Q.P., Popowicz, Z. and Tian, K. (2010) Supersymmetric Reciprocal Transformation and Its Applications. Journal of Mathematical Physics, 51, Article ID: 093511. http://dx.doi.org/10.1063/1.3481568
- 10. Ma, W.X., Xu, X.X. and Zhang, Y.F. (2006) Semi-Direct Sums of Lie Algebras and Continuous Integrable Couplings. Physics Letters A, 351, 125-130. http://dx.doi.org/10.1016/j.physleta.2005.09.087
- 11. Guo, F.K. and Zhang, Y.F. (2005) The Quadratic-Form Identity for Constructing the Hamiltonian Structure of Integrable Systems. Journal of Physics A: Mathematical and General, 38, 8537-8548. http://dx.doi.org/10.1088/0305-4470/38/40/005
- 12. Zhang, Y.F. and Tam, H.W. (2010) Four Lie Algebras Associated with R6 and Their Applications. Journal of Mathematical Physics, 51, Article ID: 093514. http://dx.doi.org/10.1063/1.3489126
- 13. Ma, W.X. (2011) Nonlinear Continuous Integrable Hamiltonian Couplings. Applied Mathematics and Computation, 217, 7238-7244. http://dx.doi.org/10.1016/j.amc.2011.02.014
- 14. You, F.C. (2011) Nonlinear Super Integrable Hamiltonian Couplings. Journal of Mathematical Physics, 52, Article ID: 123510. http://dx.doi.org/10.1063/1.3669484
- 15. Zhang, Y.F. and Zhang, H.Q. (2002) A Family of Integrable Systems of Liouville and Lax Representation, Darboux Transformation for Its Constrained Flows. Applied Mathematics and Mechanics, 23, 23-30.
- 16. Shi, H. and Tao, S.X. (2011) A Super-Integrable Hierarchy and Its Super-Hamiltonian Structure. International Journal of Nonlinear Science, 10, 12-16.
- 17. Zhang, Y.F. (2011) Lie Algebras for Constructing Nonlinear Integrable Couplings. Communications in Theoretical Physics, 56, 805-812. http://dx.doi.org/10.1088/0253-6102/56/5/03


