Received 20 December 2015; accepted 6 April 2016; published 13 April 2016

ABSTRACT

In this paper, we show that some functions related to the dual Simpson’s formula and Bullen- Simpson’s formula are Schur-convex provided that f is four-convex. These results should be compared to that of Simpson’s formula in Applied Math. Lett. (24) (2011), 1565-1568.

Keywords:

Schur Convexity, 4-Convex Function, Dual Simpson’s Formula, Bullen-Simpson’s Formula

1. Introduction

Schur convexity is an important notion in the theory of convex functions, which were introduced by Schur in 1923 ([1] [2]), its definition is stated in what follows. Let be denoted as,

,

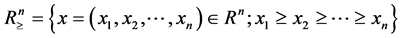and 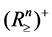be defined by,

Then we recall (see, e.g., [3]-[5]) that a function is Schur convex if

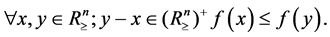
Every Schur-convex function is a symmetric function, and if I is an open interval and 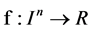is symmetric and of class, then f is Schur-convex if and only if

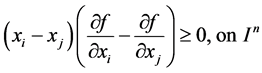(1.1)

for all.

Let 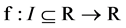be a convex function defined on the interval I of real numbers and with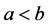. The following inequality

(1.2)

holds. This double inequality is called Hermite-Hadamard inequality for convex functions. Hermite-Hadamard inequality is improved though Schur convexity, c.f., [6]-[10]. Among these paper, it is proven that if is an interval and is continuous, then f is convex if and only if the mapping

(Here and what follows, we use the mapping convention for case, which is no longer stated.) is Schur convex, and in this case, is convex. If is an interval and is continuous, then f is convex if and only if one of the following mappings

is Schur convex. Some exciting results on Schur’s majorization inequality can be found in [11]-[13].

Let be a four times continuously differentiable mapping on [a, b]. Then the following quadrature rule is well-known:

(1.3)

which is called Simpson’s formula, c.f. [14] and [15]. For is an interval and is called four- convex, if for all. In [15], the authors proved that if is continuous, then f is four-convex is equivalent to the mappings defined by

is Schur-convex, this is an improvement of the Simpson’s formula.

On the other hand, the dual Simpson’s formula ([14]) is stated as follows: if is continuous, there exist such that

(1.4)

In [16], Bullen proved that, if f is four-convex, then the dual Simpson’s quadrature formula is more accurate than Simpson’s formula. That is, it holds that

provided that f is four-convex.

Now we can state our main results. In view of the dual Simpson’s formula and the above Bullen-Simpson formula, we construct two mappings as follows: for, we set

We shall show that if is continuous, then f is four-convex if and only if the mapping or is Schur-convex. Obviously our results improve the dual-Simpson’s formula and the Bullen- Simpson’s formula, and hence complement the main result in [15].

2. Main Results

We now present our main theorem.

Theorem 2.1. Let be a mapping on I, then the following statements are equivalent:

(a) The function is Schur-convex on.

(b) The function is Schur-convex on.

(c) The function is Schur-convex on.

(d) For any with, we have the Simpson inequality holds, i.e.:

.

(e) For any with, we have the dual Simpson inequality holds, i.e.:

.

(f) For any with, we have the Bullen-Simpson inequality holds, i.e.:

.

(g) The function f is four-convex on I.

Proof:

The equivalence of (a) (d) (g) was already proven in [15]. Suppose that item (g) holds, then by the definition of the function, we have

.

,

(by Simpson’s formula (1.4) and four-convexity of f) hence,

Here we denote, for. Since f is four-convex, h(x) is convex. Thus Hermite-Hadamard (1.2) holds for h(x) in, this gives that, so by the criteria (1.1) is Schur-convex, item (b) is a consequence of item (g).

Now suppose that item (b) holds. Since, Schur-convexity of gives that, i.e., item (e) is valid if item (b) holds.

Next we prove item (e) implies item (g). By item (e) and the dual Simpson’s formula (1.6), we get

.

Since, and a, b are arbitrary, it follows that f is four-convex. Now the equivalence of (b) (e) (g) is proven. We follow the same pattern to show the equivalence of (c) (f) (g). If item (c) holds, then, i.e., item (f) is valid. Suppose that item (f) is valid. By the definitions and formulas (1.3) and (1.4), we get

.

Since, and a, b are arbitrary, item (g) follows again. It is only left to show that item (g) implies item (c). We give a lemma first.

Lemma 2.1. Let be four-convex on I, then the following inequalities hold for any with b ≥ a:

.

.

Proof:

We only prove the first inequality. Denote that

,

and that, then

. (2.1)

.

Here,

.

.

From the Hermite-Hadamard inequality for convex function, we see that. Besides, it follows from convexity of that for any:

.

Take integration w.r.t y, we get

,

applying this inequality in, we see that. It follows that for any b ≥ a, hence by (2.1) we know for any b ≥ a. The second inequality in the lemma is just the first inequality with b ≤ a, we omit its proof. The lemma is proven.

Now we continue the proof of our main theorem. By the definition of, we have

here is denoted as

Suppose that item (g) holds, by applying the lemma to f in, we get both, thus, so by the criteria (1.1) is Schur-convex, item (c) follows.

Remark 2.1. From Lemma 2.1, we add the two inequalities together to see that the following holds for four- convex functions f:

(2.2)

it is well-known, c.f., [14] or [15].

Starting from this inequality (2.2), we deduce some properties for four-convex functions. As in the above, we define a pair of mappings by

;

.

Then we have

Theorem 2.2. Let be four-convex on I, then the mappings are non-negative and Schur-convex on I².

Proof:

We observe that

(2.3)

(2.4)

Here inequality (2.3) is due to inequality (2.2), and inequality (2.4) is a consequence of the Hermite-Hada- mard inequality for convex function, thus by the criteria (1.1) are Schur-convex on. Hence we get.

Since is non-negative, we observe that

(2.5)

It is shown in [7] for a convex function g that the function

(if)

is Schur-convex, specially we have. We set, then it is convex, we see that RHS of inequality (2.5) is non-negative, so by the criteria (1.1), is Schur-convex.

Furthermore, we give a Schur-convexity theorem for the following mapping:

.

Theorem 2.3. Let be four-convex on I, then the mappings are non-negative and Schur-convex on .

Proof: We observe that

.

Since for convex function, as in the above, we can conclude that are non- negative and Schur-convex.

Remark 2.2. For smooth four-convex functions, we see that both and are non-negative and Schur- convex functions, then the sum of and is also non-negative and Schur-convex function, especially it holds that

Remark 2.3. For positive real numbers x, y, we denote the arithmetic mean, geometric mean, and logarithmic mean of x, y by A, G, L. Applying non-negativity of and to function, then we have

.

Acknowledgements

The author is partially supported by the National Natural Science Foundation of China No-11071112.

Cite this paper

Yaowen Li, (2016) Schur Convexity and the Dual Simpson’s Formula. Journal of Applied Mathematics and Physics,04,623-629. doi: 10.4236/jamp.2016.44070

References